Tre-fas trafikteori

Tre-fas trafikteori är en teori om trafikflöde som utvecklades av Boris Kerner mellan 1996 och 2002. Den fokuserar främst på förklaringen av fysiken kring trafikavbrott och den resulterande överbelastade trafiken på motorvägar. Kerner beskriver tre faser av trafik, medan de klassiska teorierna baserade på det grundläggande diagrammet för trafikflöde har två faser: fritt flöde och överbelastad trafik . Kerners teori delar in överbelastad trafik i två distinkta faser, synkroniserat flöde och bred rörlig trafik , vilket ger det totala antalet faser till tre:

Synkroniserat flöde

Sylt

1. Fritt flöde ( F )
2. Synkroniserat flöde ( S )
3. Bred rörlig stopp ( J )

Ordet "bred" används trots att det är längden på trafikstockningen som det avses.

En fas definieras som ett tillstånd i rum och tid.

Fritt flöde ( F )

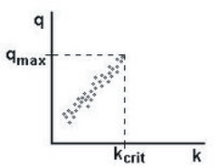
I fritt trafikflöde visar empiriska data en positiv korrelation mellan flödeshastigheten $q$ (i fordon per tidsenhet) och fordonstäthet $k$ (i fordon per enhet avstånd). Detta förhållande stannar vid det maximala fria flödet $q_{\max }$ med en motsvarande kritisk densitet $k_{\text{crit}}$ . (Se bild 1.)

Figur 1: Uppmätt flödeshastighet kontra fordonstäthet i fritt flöde (fiktiva data)

Överbelastad trafik

Data visar ett svagare samband mellan flöde och täthet i överbelastade förhållanden. Därför hävdar Kerner att det grundläggande diagrammet , som det används i klassisk trafikteori, inte på ett adekvat sätt kan beskriva den komplexa dynamiken i fordonstrafik. Han delar istället upp trängsel i synkroniserat flöde och breda rörliga jams .

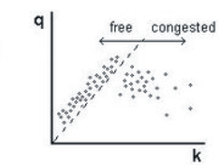
I överbelastad trafik är fordonshastigheten lägre än den lägsta fordonshastigheten $v_{\text{free}}^{\min }$ som påträffas i fritt flöde, dvs linjen med lutningen för den minimala hastigheten ${\displaystyle v_{\text{free}}^{\min }={\frac {q_{\max }}{k_{\text{crit}}}}} i fritt$ flöde (prickad linje i figur 2) delar upp empiriska data på flödestäthetsplanet i två regioner: på vänster sida datapunkter för fritt flöde och på höger sida datapunkter som motsvarar överbelastad trafik.

Figur 2: Flödeshastighet kontra fordonstäthet i fritt flöde och överbelastad trafik (fiktiva data)

Definitioner [ J ] och [ S ] av faserna J och S i överbelastad trafik

I Kerners teori är faserna J och S i överbelastad trafik observerade utfall i universella rums-temporala egenskaper hos verklig trafikdata . Faserna J och S definieras genom definitionerna [ J ] och [ S ] enligt följande:

Figur 3: Uppmätta data för hastighet i tid och rum (a) och dess representation på tid-rymdplanet (b)

Den "bred rörliga jam"-fasen [ J ]

En så kallad "wide moving jam" rör sig uppströms genom alla flaskhalsar på motorvägen . Medan detta görs bibehålls medelhastigheten för nedströmsfronten ${\displaystyle v_{g}} .$ Detta är det karakteristiska kännetecknet för den breda rörliga stoppningen som definierar fasen J .

Termen bred rörlig jam är avsedd att återspegla den karakteristiska egenskapen hos jam att fortplanta sig genom vilket annat trafikflöde som helst och genom vilken flaskhals som helst samtidigt som hastigheten på den nedströms jam fronten bibehålls. Frasen rörlig sylt återspeglar syltutbredningen som en helhet lokaliserad struktur på en väg. För att skilja breda rörliga jams från andra rörliga jams, som inte karakteristiskt bibehåller medelhastigheten för den nedströms jamfronten, använde Kerner termen wide . Termen bred återspeglar det faktum att om en trafikstockning har en bredd (i den längsgående vägriktningen) som är avsevärt större än bredden på jamfronterna, och om fordonshastigheten inuti köningen är noll, uppvisar köningen alltid den karakteristiska egenskapen att bibehålla hastigheten på den nedströms belägna jamfronten (se avsnitt 7.6.5 i boken). Termen bred har alltså ingenting att göra med bredden över sylten, utan syftar faktiskt på att dess längd är betydligt mer än övergångszonerna vid dess huvud och stjärt. Historiskt sett använde Kerner termen brett från en kvalitativ analogi av en bred rörlig stopp i trafikflödet med breda autosolitoner som förekommer i många naturvetenskapliga system (som gasplasma, elektronhålsplasma i halvledare, biologiska system och kemiska reaktioner): den breda rörliga sylten och en bred autosoliton uppvisar några karakteristiska egenskaper, som inte beror på initiala förhållanden vid vilka dessa lokaliserade mönster har uppstått.

Fasen "synkroniserat flöde" [ S ]

I "synkroniserat flöde" visar den nedströms belägna fronten, där fordonen accelererar till fritt flöde, inte denna karaktäristiska egenskap hos den breda rörliga stoppningen. Närmare bestämt är nedströmsfronten av det synkroniserade flödet ofta fixerad vid en flaskhals.

Termen "synkroniserat flöde" är avsedd att återspegla följande särdrag i denna trafikfas: (i) Det är ett kontinuerligt trafikflöde utan några betydande stopp, vilket ofta inträffar i en bred trafikstockning. Termen "flöde" återspeglar denna egenskap. (ii) Det finns en tendens till synkronisering av fordonshastigheter över olika körfält på en flerfilig väg i detta flöde. Dessutom finns det en tendens till synkronisering av fordonshastigheter i vart och ett av vägfilerna (körning av fordon) i synkroniserat flöde. Detta beror på en relativt låg sannolikhet att bli godkänd. Termen "synkroniserad" återspeglar denna hastighetssynkroniseringseffekt.

Förklaring av trafikfasdefinitionerna baserad på uppmätta trafikdata

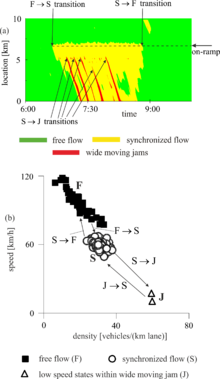
Uppmätta data för medelvärde för fordonshastigheter (Figur 3 (a)) illustrerar fasdefinitionerna [ J ] och [ S ]. Det finns två rums-temporala mönster av överbelastad trafik med låga fordonshastigheter i figur 3 (a). Ett mönster fortplantar sig uppströms med en nästan konstant hastighet på nedströmsfronten och rör sig rakt genom motorvägens flaskhals. Enligt definitionen [ J ] tillhör detta trängselmönster fasen "wide moving jam". Däremot är nedströmsfronten av det andra mönstret fixerad vid en flaskhals. Enligt definitionen [ S ] tillhör detta mönster "synkroniserat flöde"-fasen (Figur 3 (a) och (b)). Andra empiriska exempel på validering av trafikfasdefinitionerna [ J ] och [ S ] finns i böckerna och i artikeln samt i en empirisk studie av flytande bildata (flytande bildata kallas även sondfordonsdata ).

Trafikfasdefinition baserad på empiriska enfordonsdata

I Sec. 6.1 i boken har visats att trafikfasdefinitionerna [ S ] och [ J ] är ursprunget till de flesta hypoteser om trefasteori och relaterade trefasmikroskopiska trafikflödesmodeller. Trafikfasdefinitionerna [ J ] och [ S ] är icke-lokala makroskopiska sådana och de är tillämpliga endast efter att makroskopiska data har mätts i rum och tid, dvs i en "off-line" studie. Detta beror på att för den definitiva distinktionen av faserna J och S genom definitionerna [ J ] och [ S ] krävs en studie av utbredningen av trafikstockningar genom en flaskhals. Detta anses ofta vara en nackdel med trafikfasdefinitionerna [ S ] och [ J ]. Det finns dock lokala mikroskopiska kriterier för distinktionen mellan faserna J och S utan en studie av utbredningen av överbelastad trafik genom en flaskhals. De mikroskopiska kriterierna är som följer (se avsnitt 2.6 i boken): Om i enkelfordons ( mikroskopiska ) data relaterade till överbelastad trafik observeras "flödesavbrottsintervallet", dvs. en tidsförskjutning mellan två fordon som följer efter varandra , vilket är mycket längre än medeltidsfördröjningen i fordonsacceleration från en bred rörlig stopp (den senare är cirka 1,3–2,1 s), då motsvarar det relaterade flödesavbrottsintervallet den breda rörliga stoppfasen. Efter att alla breda rörliga störningar har hittats genom detta kriterium i överbelastad trafik, är alla återstående överbelastade tillstånd relaterade till den synkroniserade flödesfasen.

Kerners hypotes om tvådimensionella (2D) tillstånd av trafikflöde

Stadiga tillstånd av synkroniserat flöde

Homogent synkroniserat flöde är ett hypotetiskt tillstånd av synkroniserat flöde av identiska fordon och förare där alla fordon rör sig med samma tidsoberoende hastighet och har samma mellanrum (ett mellanrum är avståndet mellan ett fordon och det bakom det), dvs detta synkroniserade flöde är homogent i tid och rum.

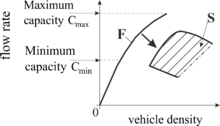
Kerners hypotes är att homogent synkroniserat flöde kan inträffa var som helst i ett tvådimensionellt område (2D) av flödestäthetsplanet (2D-region S i figur 4(a)). Uppsättningen av möjliga fritt flödestillstånd (F) överlappar i fordonstäthet med uppsättningen av möjliga tillstånd av homogent synkroniserat flöde. Tillstånden för fritt flöde på en flerfilig väg och tillstånden med homogent synkroniserat flöde separeras av ett gap i flödeshastigheten och därför av ett gap i hastigheten vid en given densitet: vid varje given täthet är den synkroniserade flödeshastigheten lägre än den fria flödeshastigheten.

I enlighet med denna hypotes om Kerners trefasteori, vid en given hastighet i synkroniserat flöde, kan föraren göra ett godtyckligt val vad gäller utrymmesgapet till det föregående fordonet, inom intervallet som är associerat med 2D-området för homogent synkroniserat flöde ( Figur 4(b)): föraren accepterar olika mellanrum vid olika tidpunkter och använder inte en unik lucka.

Figur 4: Hypotes för Kerners trefastrafikteori om 2D-region av stabila tillstånd av synkroniserat flöde i flödes-densitetsplanet: (a) Kvalitativ representation av fritt flödestillstånd (F) och 2D-region av homogent synkroniserat flöde (streckad region S ) på en flerfilig väg i flödestäthetsplanet. (b) En del av 2D-området med homogent synkroniserat flöde i rymdgaphastighetsplanet (streckat område S). I (b) är $G$ och $g_{\text{safe}}$ ett synkroniseringsutrymme respektive ett säkert utrymme mellan två fordon som följer varandra.

Hypotesen för Kerners trefastrafikteori om 2D-regionen av stabila tillstånd av synkroniserat flöde strider mot hypotesen om tidigare trafikflödesteorier som involverar det grundläggande diagrammet för trafikflöde, som antar ett endimensionellt samband mellan fordonstäthet och flödeshastighet. .

Bilföljande i trefastrafikteori

I Kerners trefasteori accelererar ett fordon när mellanrummet $g$ till det föregående fordonet är större än ett synkroniseringsutrymme $G$ , dvs vid $g>G$ (märkt med acceleration i figur 5); fordonet retarderar när gapet g är mindre än ett säkert utrymme $g_{\text{safe}}$ , dvs vid $g<g_{\rm {safe }}$ (märkt med retardation i figur 5).

Figur 5: Kvalitativ förklaring av bilföljning i Kerners trefastrafikteori: Ett fordon accelererar vid ett mellanrum $g>G$ och retarderar vid mellanrum $g<g_{ \text{safe}}$ , medan under villkoret $g_{\text{safe}}\leq g\leq G$ anpassar fordonet sin hastighet till det föregående fordonets hastighet utan att bry sig om vad det exakta mellanrummet är. Det streckade området för synkroniserat flöde är hämtat från figur 4(b).

Om gapet är mindre än G tenderar föraren att anpassa sin hastighet till det föregående fordonets hastighet utan att bry sig om vad det exakta gapet är, så länge som detta gap inte är mindre än säkerhetsutrymmet g safe {\ ${ \text{safe}}}$ (märkt med hastighetsanpassning i figur 5). Således kan utrymmesgapet $g$ i bilföljande inom ramen för Kerners trefasteori vara vilket utrymmesgap som helst inom utrymmesgapets intervall $g_{\text{safe}}\ leq g\leq G$ .

Autonom körning inom ramen för trefastrafikteori

Inom ramen för trefasteorin har hypotesen om 2D-regioner av tillstånd av synkroniserat flöde också tillämpats för utvecklingen av en modell av autonomt körande fordon (kallas även automatiserad körning , självkörande eller autonomt fordon).

Trafikavbrott – en F → S fasövergång

I uppmätta data förekommer överbelastad trafik oftast i närheten av flaskhalsar på motorvägar, t.ex. påfarter, avfarter eller vägarbeten. En övergång från fritt flöde till överbelastad trafik kallas trafikavbrott. I Kerners trefastrafikteori förklaras trafiknedbrytning av en fasövergång från fritt flöde till synkroniserat flöde (kallas F →S fasövergång). Denna förklaring stöds av tillgängliga mätningar, eftersom i uppmätta trafikdata efter ett trafikavbrott vid en flaskhals är nedströmsfronten av den överbelastade trafiken fixerad vid flaskhalsen. Därför uppfyller den resulterande överbelastade trafiken efter ett trafikavbrott definitionen [ S ] av fasen "synkroniserat flöde".

Empiriska spontana och inducerade F → S -övergångar

Kerner noterar med hjälp av empiriska data att synkroniserat flöde kan bildas i fritt flöde spontant (spontan F → S fasövergång) eller kan induceras externt (inducerad F → S fasövergång).

En spontan F →S fasövergång innebär att haveriet sker när det tidigare har varit fritt flöde vid flaskhalsen samt både upp- och nedströms flaskhalsen. Detta innebär att en spontan F → S-fasövergång sker genom tillväxten av en intern störning i fritt flöde i närheten av en flaskhals.

Däremot sker en inducerad F → S-fasövergång genom en region med överbelastad trafik som initialt dök upp vid en annan vägplats nedströms från flaskhalsplatsen. Normalt är detta i samband med uppströms utbredning av ett synkroniserat flödesområde eller en bred rörlig stopp. Ett empiriskt exempel på ett inducerat haveri vid en flaskhals som leder till synkroniserat flöde kan ses i figur 3: synkroniserat flöde uppstår genom uppströms utbredning av en bred rörlig stopp. Förekomsten av empiriskt inducerad trafikavbrott (dvs empiriskt inducerad F →S fasövergång) innebär att en F → S fasövergång sker i ett metastabilt tillstånd av fritt flöde vid en motorvägsflaskhals. Termen metastabilt fritt flöde innebär att när små störningar uppstår i fritt flöde är tillståndet för fritt flöde fortfarande stabilt, dvs. fritt flöde kvarstår vid flaskhalsen. Men när större störningar inträffar i fritt flöde i närheten av flaskhalsen är det fria flödet instabilt och synkroniserat flöde kommer att uppstå vid flaskhalsen.

Fysisk förklaring av trafikavbrott i trefasteori

Figur 6: Förklaring av trafikavbrott med en Z-liknande icke-linjär avbruten funktion av sannolikheten för omkörning i Kerners trefastrafikteori. Den prickade kurvan illustrerar den kritiska sannolikheten för omkörning som en funktion av trafiktätheten.

Kerner förklarar karaktären av F → S fasövergångar som en konkurrens mellan "hastighetsanpassning" och "överacceleration". Hastighetsanpassning definieras som fordonets retardation till hastigheten hos ett tidigare fordon som rör sig långsammare. Överacceleration definieras som fordonets acceleration även om det föregående fordonet inte kör snabbare än fordonet och det föregående fordonet dessutom inte accelererar. I Kerners teori är sannolikheten för överacceleration en diskontinuerlig funktion av fordonshastigheten: Vid samma fordonstäthet är sannolikheten för överacceleration i fritt flöde större än vid synkroniserat flöde. När inom en lokal hastighetsstörning hastighetsanpassning är starkare än överacceleration, inträffar en F → S fasövergång. Annars, när överaccelerationen är starkare än hastighetsanpassningen, avtar den initiala störningen med tiden. Inom ett område med synkroniserat flöde är en kraftig överacceleration ansvarig för en returövergång från synkroniserat flöde till fritt flöde (S → F-övergång).

Det kan finnas flera mekanismer för fordonsöveracceleration. Det kan antas att den mest sannolika mekanismen för överacceleration på en flerfilig väg är filbyte till ett snabbare körfält. I detta fall förklaras fasövergångarna F → S av ett samspel av acceleration vid omkörning av ett långsammare fordon (överacceleration) och inbromsning till hastigheten för ett långsammare fordon framför (hastighetsanpassning). Omkörningar stöder upprätthållandet av fritt flöde. "Hastighetsanpassning" leder å andra sidan till synkroniserat flöde. Hastighetsanpassning kommer att ske om omkörning inte är möjlig. Kerner anger att sannolikheten för omkörning är en avbruten funktion av fordonstätheten (Figur 6): vid en given fordonstäthet är sannolikheten för omkörning i fritt flöde mycket högre än i synkroniserat flöde.

Diskussion om Kerners förklaring av trafikavbrott

Kerners förklaring av trafikavbrott vid en flaskhals på motorväg genom F → S-fasövergången i ett metastabilt fritt flöde är associerad med följande grundläggande empiriska egenskaper hos trafikavbrott vid flaskhalsen som finns i verkliga uppmätta data: (i) Spontant trafikavbrott i en initial fritt flöde vid flaskhalsen leder till uppkomsten av överbelastad trafik vars nedströmsfront är fixerad vid flaskhalsen (åtminstone under ett visst tidsintervall), dvs. denna överbelastade trafik uppfyller definitionen [S] för den synkroniserade flödesfasen. Med andra ord är spontan trafikavbrott alltid en F → S fasövergång. (ii) Sannolikheten för detta spontana trafikavbrott är en ökande funktion av flödeshastigheterna vid flaskhalsen. (iii) Vid samma flaskhals kan trafikavbrott vara antingen spontant eller inducerat (se empiriska exempel för dessa grundläggande egenskaper hos trafikavbrott i avsnitt 2.2.3 och 3.1 i boken); av denna anledning sker F → S-fasövergången i ett metastabilt fritt flöde vid en flaskhals på motorvägen. Såsom förklarats ovan är innebörden av termen metastabilt fritt flöde som följer. Tillräckligt små störningar i metastabilt fritt flödesavfall. Men när en tillräckligt stor störning inträffar vid flaskhalsen, inträffar en F → S fasövergång. En sådan störning som initierar F → S fasövergången i metastabilt fritt flöde vid flaskhalsen kan kallas en kärna för trafikavbrott. Med andra ord uppvisar verklig trafiknedbrytning (F → S-fasövergång) vid en flaskhals på motorvägen kärnbildningskaraktären . Kerner betraktar den empiriska kärnbildningskaraktären av trafikavbrott (F → S fasövergång) vid en vägflaskhals som den empiriska grunden för trafik- och transportvetenskap.

Anledningen till Kerners teori och hans kritik av klassiska trafikflödesteorier

Den empiriska kärnbildningskaraktären av trafikavbrott vid motorvägsflaskhalsar kan inte förklaras av klassiska trafikteorier och -modeller. Sökandet efter en förklaring av den empiriska kärnbildningskaraktären av trafiknedbrytning (F → S-fasövergång) vid en flaskhals på motorvägen har varit motivationen för utvecklingen av Kerners trefasteori.

I synnerhet i tvåfasiga trafikflödesmodeller där trafikavbrott är förknippat med fritt flödesinstabilitet, leder denna modellinstabilitet till F → J fasövergången, dvs i dessa trafikflödesmodeller styrs trafikavbrott av spontan uppkomst av en bred rörlig jam(er) i ett initialt fritt flöde (se Kerners kritik av sådana tvåfasmodeller såväl som på andra klassiska trafikflödesmodeller och teorier i kapitel 10 i boken samt i kritiska recensioner).

Huvudförutsägelsen av Kerners trefasteori

Kerner utvecklade trefasteorin som en förklaring av den empiriska karaktären av trafikavbrott vid motorvägsflaskhalsar: en slumpmässig (probabilistisk) F → S fasövergång som inträffar i det metastabila tillståndet av fritt flöde. Härmed förklarade Kerner huvudförutsägelsen, att denna metastabilitet för fritt flöde med avseende på F → S fasövergången styrs av kärnbildningsnaturen hos en instabilitet av synkroniserat flöde. Förklaringen är en tillräckligt stor lokal hastighetsökning i synkroniserat flöde (kallad S → F-instabilitet), vilket är en växande hastighetsvåg av en lokal hastighetsökning i synkroniserat flöde vid flaskhalsen. Utvecklingen av S → F-instabiliteten leder till en lokal fasövergång från synkroniserat flöde till fritt flöde vid flaskhalsen (S → F-övergång). För att förklara detta fenomen utvecklade Kerner en mikroskopisk teori om S → F instabilitet. Ingen av de klassiska trafikflödesteorierna och -modellerna inkluderar S → F-instabiliteten hos trefasteorin.

Kerner, som ursprungligen utvecklades för motorvägstrafik, utökade trefasteorin för beskrivningen av stadstrafik 2011–2014.

Utbud av motorvägskapacitet

I trefastrafikteorin förklaras trafikavbrott av F → S-övergången som sker i ett metastabilt fritt flöde. Den förmodligen viktigaste konsekvensen av detta är förekomsten av en rad motorvägskapaciteter mellan vissa maximala och minimala kapaciteter.

Maximal och minimal motorvägskapacitet

Spontant trafikavbrott, dvs. en spontan F → S-fasövergång, kan inträffa inom ett brett område av flödeshastigheter i fritt flöde. Kerner konstaterar, baserat på empiriska data, att på grund av möjligheten till spontana eller inducerade trafikavbrott vid samma motorvägsflaskhals när som helst finns det en rad motorvägskapaciteter vid en flaskhals. Detta område av motorvägskapaciteter är mellan en minimikapacitet $C_{\min }$ och en maximal kapacitet $C_{\max }$ för fritt flöde (Figur 7).

Figur 7: Maximal och minimal motorvägskapacitet i Kerners trefastrafikteori

Motorvägskapacitet och metastabilitet för fritt flöde

Det finns en maximal motorvägskapacitet $C_{\max }$ : Om flödeshastigheten är nära den maximala kapaciteten ${\displaystyle C_{\max }},$ då även små störningar i fritt flöde vid en flaskhals kommer att leda till en spontan F → S fasövergång. Å andra sidan kommer endast mycket stora störningar i fritt flöde vid flaskhalsen att leda till en spontan F → S fasövergång, om flödet är nära en minimikapacitet C $\displaystyle C_{\min }}$ (se, till exempel avsnitt 17.2.2 i boken). Sannolikheten för en mindre störning i fritt flöde är mycket högre än för en större störning. Därför, ju högre flödeshastigheten är i fritt flöde vid en flaskhals, desto högre är sannolikheten för den spontana F → S fasövergången. Om flödeshastigheten i fritt flöde är lägre än den lägsta kapaciteten $C_{\min }$ kommer det inte att uppstå trafikavbrott (ingen F →S fasövergång) vid flaskhalsen.

Det oändliga antalet motorvägskapaciteter vid en flaskhals kan illustreras av metastabiliteten hos fritt flöde vid flödeshastigheter $q$ med

$C_{\min }\leq q<C_{\max }.$

Metastabilitet av fritt flöde innebär att fritt flöde för små störningar förblir stabilt (fritt flöde kvarstår), men vid större störningar blir flödet instabilt och en F → S fasövergång till synkroniserat flöde sker.

Diskussion av kapacitetsdefinitioner

Således är det grundläggande teoretiska resultatet av trefasteori om förståelsen av den stokastiska kapaciteten av fritt flöde vid en flaskhals som följer: När som helst finns det ett oändligt antal motorvägskapaciteter för fritt flöde vid flaskhalsen. Det oändliga antalet flödeshastigheter, vid vilka trafikavbrott kan induceras vid flaskhalsen och det oändliga antalet motorvägskapaciteter. Dessa kapaciteter ligger inom flödeshastighetsintervallet mellan en minimikapacitet och en maximal kapacitet (Figur 7).

Utbudet av motorvägskapaciteter vid en flaskhals i Kerners trefastrafikteori motsäger i grunden den klassiska förståelsen av stokastisk motorvägskapacitet samt trafikteorier och metoder för trafikledning och trafikledning som när som helst antar att det finns en viss motorvägskapacitet . Däremot finns det i Kerners trefastrafikteori ett intervall av motorvägskapaciteter, som ligger mellan minimikapaciteten $C_{\min }$ och maximal kapacitet $C_{\max }$ . Värdena $C_{\min }$ och $C_{\max }$ kan avsevärt bero på trafikparametrar (andelen långa fordon i trafikflöde, väder, flaskhalsegenskaper, etc.).

Förekomsten av en rad motorvägskapaciteter när som helst i Kerners teori förändrar avgörande metoder för trafikkontroll, dynamisk trafiktilldelning och trafikledning. I synnerhet, för att tillfredsställa kärnbildningskaraktären av trafikavbrott, introducerade Kerner principen för minimering av sammanbrott (BM-principen) för optimering och kontroll av fordonstrafiknätverk.

Breda rörliga stopp ( J )

En rörlig stopp kommer att kallas "bred" om dess längd (i flödesriktningen) klart överstiger längden på stoppfronterna. Den genomsnittliga fordonshastigheten inom breda rörliga köer är mycket lägre än medelhastigheten i fritt flöde. Vid fronten nedströms accelererar fordonen till fritt flöde. Vid uppströms jamfronten kommer fordonen från fritt flöde eller synkroniserat flöde och måste minska sin hastighet. Enligt definitionen [ J ] har den breda rörelsestockningen alltid samma medelhastighet som den nedströms belägna fronten $v_{g}$ , även om störningen fortplantar sig genom andra trafikfaser eller flaskhalsar. Flödeshastigheten reduceras kraftigt inom en bred rörlig stopp.

Karakteristiska parametrar för breda rörliga sylt

Kerners empiriska resultat visar att vissa karakteristiska egenskaper hos breda trafikstockningar är oberoende av trafikvolymen och flaskhalsdragen (t.ex. var och när jammen bildades). Dessa karakteristiska egenskaper är dock beroende av väderförhållanden, vägförhållanden, fordonsteknik, andel långa fordon, etc. Hastigheten för nedströmsfronten av en bred rörlig stopp v g {\ ${g}}$ (uppströms riktning) är en karakteristisk parameter, liksom flödeshastigheten precis nedströms om jam $q_{\text{out}}$ (med fritt flöde på denna plats, se figur 8). Detta innebär att många brett rörliga pappersstopp har liknande egenskaper under liknande förhållanden. Dessa parametrar är relativt förutsägbara. Rörelsen av den nedströms belägna blockeringsfronten kan illustreras i flödestäthetsplanet med en linje, som kallas "Linje J" (Linje J i figur 8). Lutningen på linje J är hastigheten för nedströms jamfront $v_{g}$ .

Figur 8: Tre trafikfaser på flödestäthetsplanet i Kerners trefastrafikteori

Minsta motorvägskapacitet och utflöde från bred rörlig stopp

Kerner betonar att minimikapaciteten $C_{\min }$ och utflödet av en bred rörlig stopp $q_{\text{out}}$ beskriver två kvalitativt olika egenskaper hos fritt flöde: minimum kapacitet $C_{\min }$ kännetecknar en F → S fasövergång vid en flaskhals, dvs ett trafikavbrott. Däremot bestämmer utflödet av en bred rörlig stopp $q_{\text{out}}$ ett villkor för existensen av den breda rörelsestockningen, dvs. trafikfasen J medan köningen fortplantar sig i fritt flöde: Faktum är att om sylten fortplantar sig genom fritt flöde (dvs. både uppströms och nedströms de syltfria flödena uppstår), så kan en bred rörlig stopp kvarstå, endast när syltinflödet q i {\displaystyle q_{\text $} }}$ är lika med eller större än syltutflödet $q_{\text{out}}$ ; annars löses sylten upp med tiden. Beroende på trafikparametrar som väder, andel långa fordon, et cetera, och egenskaperna hos flaskhalsen där F → S-fasövergången kan inträffa, kan minimikapaciteten $C_{\min }$ vara mindre (som i Figur 8), eller större än pappersstoppets utflöde $q_{\text{out}}$ .

Synkroniserad flödesfas ( S )

I motsats till breda rörliga stopp kan både flödeshastigheten och fordonshastigheten variera avsevärt i den synkroniserade flödesfasen. Nedströmsfronten av synkroniserat flöde är ofta rumsligt fixerad (se definition [ S ]), normalt vid en flaskhals vid en viss vägplats. Flödeshastigheten i denna fas kan förbli liknande den i fritt flöde, även om fordonshastigheterna sänks kraftigt.

Eftersom den synkroniserade flödesfasen inte har de karakteristiska egenskaperna hos den breda rörliga stoppfasen J , antar Kerners trefastrafikteori att de hypotetiska homogena tillstånden för synkroniserat flöde täcker ett tvådimensionellt område i flödestäthetsplanet (streckade områden i Figur 8).

S → J fasövergång

Breda rörliga stopp uppstår inte spontant i fritt flöde, men de kan uppstå i områden med synkroniserat flöde. Denna fasövergång kallas en S → J fasövergång.

"Stopp utan uppenbar anledning" – F → S → J fasövergångar

Figur 9: Empiriskt exempel på kaskad av F → S → J-fasövergångar i Kerners trefastrafikteori: (a) Fasövergångar som sker i rum och tid. (b) Representationen av samma fasövergångar som de i (a) i hastighetstäthetsplanet (pilarna S → F, J → S och J → F visar möjliga fasövergångar).

År 1998 upptäckte Kerner att i verkliga fälttrafikdata observeras uppkomsten av en bred rörlig stopp i fritt flöde som en kaskad av F → S → J fasövergångar (Figur 9): för det första uppstår ett område med synkroniserat flöde i en område med fritt flöde. Som förklarats ovan sker en sådan F → S-fasövergång mestadels vid en flaskhals. Inom den synkroniserade flödesfasen sker en ytterligare "självkomprimering" och fordonstätheten ökar medan fordonshastigheten minskar. Denna självkomprimering kallas "pinch effect". I "nypa" områden med synkroniserat flöde, uppstår smala rörliga störningar. Om dessa smala rörliga stopp växer fram kommer breda rörliga stopp märkta med S → J i figur 9). Sålunda uppstår breda trafikstockningar senare än trafikavbrott (F → S-övergång) har inträffat och vid en annan vägplats uppströms flaskhalsen. Därför, när Kerners F → S → J fasövergångar som inträffar i verklig trafik (Figur 9 (a)) presenteras i hastighetstäthetsplanet (Figur 9 (b)) (eller hastighetsflöde, eller annars flödestäthetsplan) , bör man komma ihåg att tillstånd av synkroniserat flöde och låghastighetstillstånd inom en bred rörlig stopp mäts på olika vägplatser. Kerner noterar att frekvensen av uppkomsten av breda rörliga störningar ökar om tätheten i synkroniserat flöde ökar. De breda rörliga störningarna fortplantar sig längre uppströms, även om de fortplantar sig genom områden med synkroniserat flöde eller flaskhalsar. Uppenbarligen är vilken kombination som helst av returfasövergångar (S -> F, J -> S och J -> F-övergångar som visas i figur 9) också möjliga.

Fysiken för S → J -övergången

För att ytterligare illustrera S → J fasövergångar: i Kerners trefastrafikteori delar linje J de homogena tillstånden av synkroniserat flöde i två (Figur 8). Tillstånd med homogent synkroniserat flöde ovanför linje J är metastabila. Tillstånd med homogent synkroniserat flöde under linje J är stabila tillstånd i vilka ingen S → J fasövergång kan inträffa. Metastabilt homogent synkroniserat flöde innebär att trafiktillståndet förblir stabilt vid små störningar. Men när större störningar inträffar blir synkroniserat flöde instabilt och en S → J fasövergång inträffar.

Trafikmönster för S och J

Mycket komplexa överbelastade mönster kan observeras, orsakade av F → S och S → J fasövergångar.

Klassificering av synkroniserade flödestrafikmönster (SP)

Ett trängselmönster av synkroniserat flöde (Synchronized Flow Pattern (SP)) med en fast nedströms och en inte kontinuerligt fortplantande uppströmsfront kallas Localized Synchronized Flow Pattern (LSP).

Ofta fortplantar sig uppströmsfronten av en SP uppströms. Om endast uppströmsfronten fortplantar sig uppströms kallas den relaterade SP:n Widening Synchronized Flow Pattern (WSP). Nedströmsfronten förblir vid flaskhalsen och bredden på SP ökar.

Det är möjligt att både uppströms och nedströms front fortplantar sig uppströms. Nedströmsfronten är inte längre placerad vid flaskhalsen. Detta mönster har kallats Moving Synchronized Flow Pattern (MSP).

Fånga effekt av synkroniserat flöde vid en motorvägsflaskhals

Skillnaden mellan SP och den breda rörliga jammen blir synlig genom att när en WSP eller MSP når en uppströms flaskhals kan den så kallade "catch-effekten" uppstå. SP kommer att fångas vid flaskhalsen och som ett resultat uppstår ett nytt överbelastat mönster. En brett rörlig stopp kommer inte att fångas vid en flaskhals och rör sig längre uppströms. I motsats till breda rörliga störningar har det synkroniserade flödet, även om det rör sig som en MSP, inga karakteristiska parametrar. Som ett exempel kan hastigheten på nedströmsfronten av MSP:n variera avsevärt och kan vara olika för olika MSP:er. Dessa egenskaper hos SP och breda rörliga störningar är konsekvenser av fasdefinitionerna [S] och [J].

Allmänt trafikmönster (GP)

Ett ofta förekommande trängselmönster är ett som innehåller både överbelastade faser, [S] och [J]. Ett sådant mönster med [S] och [J] kallas General Pattern (GP). Ett empiriskt exempel på GP visas i figur 9 (a).

Figur 10: Uppmätt EGP vid tre flaskhalsar $B_{1}$ , $B_{2}$ och $B_{3}$

I många motorvägsinfrastrukturer ligger flaskhalsar väldigt nära varandra. Ett trängselmönster vars synkroniserade flöde täcker två eller flera flaskhalsar kallas ett utökat mönster (EP). En EP kan endast innehålla synkroniserat flöde (kallas ESP: Expanded Synchronized Flow Pattern)), men normalt bildas breda rörliga störningar i det synkroniserade flödet. I de fallen kallas EP:n EGP (Expanded General Pattern) (se figur 10).

Tillämpningar av trefastrafikteori inom transportteknik

Figur 11: Trafikmönster i ASDA/FOTO-applikationen i tre länder

En av tillämpningarna av Kerners trefastrafikteori är metoderna som kallas ASDA/FOTO ( A utomatische S tau Dynamik A nalyse (Automatic tracking of wide moving jams) and Proecasting O f T raffic O bjects ) . ASDA/FOTO är ett mjukvaruverktyg som kan bearbeta stora trafikdatavolymer snabbt och effektivt på motorvägsnät (se exempel från tre länder, figur 11). ASDA/FOTO arbetar i ett online trafikledningssystem baserat på uppmätta trafikdata. Igenkänning, spårning och förutsägelse av [S] och [J] utförs med hjälp av funktionerna i Kerners trefastrafikteori.

Ytterligare tillämpningar av teorin ses i utvecklingen av trafiksimuleringsmodeller, ett rampmätsystem (ANCONA), kollektiv trafikkontroll, trafikassistans, autonom körning och trafiktillståndsdetektering, som beskrivs i Kerners böcker.

Matematiska modeller av trafikflöde inom ramen för Kerners trefastrafikteori

Snarare än en matematisk modell av trafikflöde , är Kerners trefasteori en kvalitativ trafikflödesteori som består av flera hypoteser. Hypoteserna i Kerners trefasteori bör kvalitativt förklara spatiotemporala trafikfenomen i trafiknätverk som finns i verkliga fälttrafikdata, som mättes över år på en mängd olika motorvägar i olika länder. Några av hypoteserna i Kerners teori har övervägts ovan. Det kan förväntas att en mångfald olika matematiska modeller av trafikflöde kan utvecklas inom ramen för Kerners trefasteori.

Den första matematiska modellen av trafikflöde inom ramen för Kerners trefasteori att matematiska simuleringar kan visa och förklara trafikavbrott genom en F → S fasövergång i det metastabila fria flödet vid flaskhalsen var Kerner-Klenov-modellen som introducerades 2002. Kerner–Klenov-modellen är en mikroskopisk stokastisk modell inom ramen för Kerners trefastrafikteori. I Kerner-Klenov-modellen rör sig fordon i enlighet med stokastiska regler för fordonsrörelse som kan väljas individuellt för vart och ett av fordonen. Några månader senare utvecklade Kerner, Klenov och Wolf en cellulär automat (CA) trafikflödesmodell inom ramen för Kerners trefasteori.

Kerner-Klenovs stokastiska trefastrafikflödesmodell inom ramen för Kerners teori har vidareutvecklats för olika tillämpningar. I synnerhet för att simulera påfartsmätning, hastighetsbegränsning, dynamisk trafiktilldelning i trafik- och transportnätverk, trafik vid tunga flaskhalsar och rörliga flaskhalsar, egenskaper hos heterogena trafikflöden som består av olika fordon och förare, kövarningsmetoder, fordon -till-fordon (V2V) kommunikation för samkörning, prestanda hos självkörande fordon i blandat trafikflöde, trafikavbrott vid signaler i stadstrafik, övermättad stadstrafik, fordons bränsleförbrukning i trafiknät (se hänvisningar i avsnitt. 1.7 av en recension).

Med tiden har flera vetenskapliga grupper utvecklat nya matematiska modeller inom ramen för Kerners trefasteori. I synnerhet har nya matematiska modeller inom ramen för Kerners trefasteori introducerats i verk av Jiang, Wu, Gao, et al., Davis, Lee, Barlovich, Schreckenberg och Kim (se andra referenser till matematiska modeller i ramverket för Kerners trefastrafikteori och resultaten av deras undersökningar i avsnitt 1.7 i en översikt).

Kritik mot teorin

Teorin har kritiserats av två primära skäl. För det första är teorin nästan helt baserad på mätningar på Bundesautobahn 5 i Tyskland. Det kan vara så att denna väg har detta mönster, men andra vägar i andra länder har andra egenskaper. Framtida forskning måste visa teorins giltighet på andra vägar i andra länder runt om i världen. För det andra är det inte klart hur data interpolerades . Kerner använder fastpunktsmätningar ( loopdetektorer ), men drar sina slutsatser om fordonsbanor, som sträcker sig över hela vägen som undersöks. Dessa banor kan endast mätas direkt om flytande bildata används, men som sagt används endast loopdetektormätningar. Hur data däremellan samlades in eller interpolerades är inte klart.

Ovanstående kritik har besvarats i en nyligen genomförd studie av data uppmätt i USA och Storbritannien, som bekräftar slutsatser gjorda baserade på mätningar på Bundesautobahn 5 i Tyskland. Dessutom finns det en nyligen genomförd validering av teorin baserad på flytande bildata. I denna artikel kan man också hitta metoder för rums-temporala interpolationer av data uppmätt vid vägdetektorer (se artikelns bilagor).

Annan kritik har framförts, som att begreppet faser inte är väldefinierat och att så kallade tvåfasmodeller också lyckas simulera de väsentliga egenskaper som Kerner beskriver.

Denna kritik har besvarats i en recension enligt följande. Det viktigaste inslaget i Kerners teori är förklaringen av den empiriska kärnbildningskaraktären av trafikavbrott vid en vägflaskhals av F → S-övergången. Den empiriska kärnbildningskaraktären av trafikavbrott kan inte förklaras med tidigare trafikflödesteorier inklusive tvåfasiga trafikflödesmodeller som studerats i.

Se även

• Aktiv trafikledning
• Grundläggande diagram
• Intelligent transportsystem
• Mikroskopisk trafikflödesmodell
• Trafikflaskhals
• Trafikflöde
• Trafikmodell
• Trafikvåg
• Trafikstockningar
• Trafikstockning: Rekonstruktion med Kerners trefasteori
• Kerners princip för nedbrytningsminimering
• Transportprognoser
• Tvåvätskemodell

Anteckningar

• Lieu, Henry (2005). "The Physics of Traffic: Empirical Freeway Pattern Features, Engineering Applications and Theory". Fysik idag . 58 (11): 54–56. Bibcode : 2005PhT....58k..54K . doi : 10.1063/1.2155762 .
•   Gao, Kun; Jiang, Rui; Hu, Shou-Xin; Wang, Bing-Hong; Wu, Qing-Song (2007). "Cellulär-automatmodell med hastighetsanpassning inom ramen för Kerners trefastrafikteori". Fysisk granskning E . 76 (2): 026105. Bibcode : 2007PhRvE..76b6105G . doi : 10.1103/PhysRevE.76.026105 . PMID 17930102 .
•   Schönhof, Martin; Helbing, Dirk (2009). "Kritik mot trefastrafikteori" (PDF) . Transportforskning Del B: Metodologisk . 43 (7): 784. CiteSeerX 10.1.1.475.3565 . doi : 10.1016/j.trb.2009.02.004 .
• H. Rehborn, S. Klenov, "Traffic Prediction of Congested Patterns", I: R. Meyers (Ed.): Encyclopedia of Complexity and Systems Science, Springer New York, 2009.
• H. Rehborn, J. Palmer, "Att använda ASDA och FOTO för att generera RDS/TMC-trafikmeddelanden", Traffic Engineering and Control, juli 2008, s. 261–266.
• Davis, L. Craig (2010). "Introduktion till modern trafikflödesteori och kontroll: Den långa vägen till trefastrafikteori" . Fysik idag . 63 (3): 53. Bibcode : 2010PhT....63c..53K . doi : 10.1063/1.3366241 .
•    Treiber, Martin; Kesting, Arne; Helbing, Dirk (2010). "Tre-fas trafikteori och tvåfasmodeller med ett grundläggande diagram i ljuset av empiriska stiliserade fakta" . Transportforskning Del B: Metodologisk . 44 (8–9): 983. arXiv : 1004.5545 . Bibcode : 2010arXiv1004.5545T . CiteSeerX 10.1.1.186.2970 . doi : 10.1016/j.trb.2010.03.004 . S2CID 18335270 .
•   Hartenstein, Hannes (2010). "Fordonstrafikflödesteori: tre, inte två faser [recension av "Introduktion till modern trafikflödesteori och kontroll: Den långa vägen till trefastrafikteori; Kerner, BS; 2009) ]". IEEE Vehicular Technology Magazine . 5 (3): 91. doi : 10.1109/MVT.2010.937837 . S2CID 21113397 .