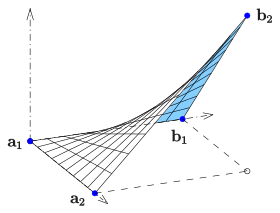
Regerad yta

Definition av en reglerad yta: varje punkt ligger på en linje

Inom geometrin styrs en yta S (även kallad en rullning ) om det genom varje punkt av S finns en rät linje som ligger på S. Exempel inkluderar planet , den laterala ytan av en cylinder eller kon , en konisk yta med elliptisk riktning , den högra konoiden , skruvlinjeformen och tangenten som kan utvecklas för en jämn kurva i rymden.

En styrd yta kan beskrivas som en uppsättning punkter som svepas av en rörlig rät linje. Till exempel bildas en kon genom att hålla en punkt på en linje fixerad samtidigt som en annan punkt flyttas längs en cirkel . En yta är dubbelstyrd om det genom var och en av dess punkter finns två distinkta linjer som ligger på ytan. Den hyperboliska paraboloiden och hyperboloiden i ett ark är dubbelt styrda ytor. Planet är den enda ytan som innehåller minst tre distinkta linjer genom var och en av sina punkter ( Fuchs & Tabachnikov 2007) .

Egenskaperna för att vara styrd eller dubbelstyrd bevaras av projektiva kartor , och är därför begrepp för projektiv geometri . Inom algebraisk geometri anses styrda ytor ibland vara ytor i affint eller projektivt utrymme över ett fält , men de betraktas också ibland som abstrakta algebraiska ytor utan inbäddning i affint eller projektivt utrymme, i vilket fall "rät linje" förstås som betyder en affin eller projektiv linje.

Definition och parametrisk representation

Styrd yta genererad av två Bézier-kurvor som riktlinjer (röd, grön)

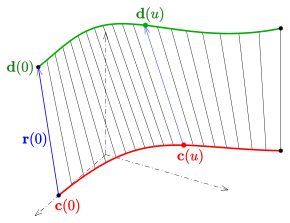
Ett tvådimensionellt differentierbart grenrör kallas en reglerad yta om det är föreningen av en parametrisk familj av linjer. Linjerna i denna familj är generatorerna av den härskade ytan.

En reglerad yta kan beskrivas med en parametrisk representation av formen

• (CR) $\quad \mathbf {x} (u,v)={\color {red}\mathbf { c} (u)}+v\;{\color {blå}\mathbf {r} (u)}\ ,\ v\in \mathbb {R} \ ,$ .

Valfri kurva $\;v\mapsto \mathbf {x} (u_{0},v)\;$ med fast parameter $u=u_{0}$ är en generator (linje) och kurvan $\;u\mapsto \mathbf {c} (u)\;$ är representationens riktning . Vektorerna $\;\mathbf {r} (u)\neq {\bf {0\;}}$ beskriver riktningarna för generatorerna.

Direktören kan kollapsa till en punkt (vid en kon, se exempel nedan).

Alternativt kan den reglerade ytan (CR) beskrivas med

• (CD) $\quad \mathbf {x} (u,v)=(1-v)\;{\ färg {röd}\mathbf {c} (u)}+v\;{\color {grön}\mathbf {d} (u)}\$

med den andra riktningen $\;\mathbf {d} (u)=\mathbf {c} (u)+\mathbf {r} (u)\ ;$ .

Alternativt kan man börja med två icke-korsande kurvor $\mathbf {c} (u),\mathbf {d} (u)$ som direktpriser, och komma med (CD) a linjerad yta med linjeriktningar $\;\mathbf {r} (u)=\mathbf {d} (u)-\mathbf {c} (u)\ .$

För generering av en styrd yta av två riktlinjer (eller en riktlinje och vektorerna för linjeriktningar) är inte bara den geometriska formen på dessa kurvor väsentliga utan även de speciella parametriska representationerna av dem påverkar formen på den styrda ytan (se exempel a ), d)).

För teoretiska undersökningar är representation (CR) mer fördelaktig, eftersom parametern $v$ endast förekommer en gång.

Exempel

cylinder, kon

Höger cirkulär cylinder

Huvudartikel: Höger cirkulär cylinder

$\ x^{2}+y^{2}=a^{2}\$ :

$\mathbf {x} (u,v)=(a\cos u,a\sin u,v)^{ T}$

$={\color {red}(a\cos u,a\sin u,0)^{ T}}\;+\;v\;{\color {blå}(0,0,1)^{T}}$

$=(1-v)\;{\color {röd}(a\cos u,a\sin u,0)^{T}}\;+\;v\;{\color {grön}( a\cos u,a\sin u,1)^{T}}\ .$

med

$\mathbf {c} (u)=(a\cos u,a\sin u,0)^{T}\ ,\ \mathbf {r} (u)=(0,0,1)^{ T}\ ,\ \mathbf {d} (u)=(a\cos u,a\sin u,1)^{T}\ .$

Höger cirkulär kon

Huvudartikel: Höger cirkulär kon

$\ x^{2}+y^{2}=z^{2}\$ :

$\mathbf {x} (u,v)=(\cos u,\sin u,1)^{T}\;+\;v\;(\cos u,\sin u,1)^{T}$

$=(1-v)\;(\cos u,\sin u,1)^{T}\;+\;v\;(2\cos u,2\sin u,2)^{T }.$

med $\quad \mathbf {c} (u)=(\cos u,\sin u,1)^{T}\;=\;\mathbf {r} (u)\ ,\quad \mathbf {d } (u)=(2\cos u,2\sin u,2)^{T}\ .$ I det här fallet kunde man ha använt spetsen som riktlinje, dvs: $\ \mathbf {c} (u)=(0,0,0)^{T}\$ och $\ \mathbf {r} (u)=(\cos u,\sin u,1)^{T}\$ som linjeriktningarna.

För varje kon kan man välja spetsen som riktlinje. Det här fallet visar: Riktningen av en reglerad yta kan degenerera till en punkt .

helikoid

Helicoid

Huvudartikel: Helicoid

$\mathbf {x} (u,v)=\;(v\cos u,v\sin u,ku )^{T}\;$

$=\;(0,0,ku)^{T}\;+\ ;v\;(\cos u,\sin u,0)^{T}\$

$=\;(1-v)\;(0,0,ku)^{T}\;+\;v\;(\cos u,\sin u,ku)^{T}\ .$

Riktningen $\ \mathbf {c} (u)=(0,0,ku)^{T}\;$ är z-axeln, linjeriktningarna är $\;\mathbf {r} (u)=\ (\cos u,\sin u,0)^{T}\;$ och den andra riktningen $\ \mathbf {d} (u)=(\cos u,\sin u,ku)^{T} \$ är en helix .

Helicoiden är ett specialfall av de härskade generaliserade helikoiderna .

Cylinder, kon och hyperboloider

Ytterligare information: Hyperboloid

hyperboloid av ett ark för $\varphi =63^{\circ }$

Den parametriska representationen

$\mathbf {x} (u,v)=(1-v)\;(\cos(u-\varphi ),\sin(u-\varphi ),-1)^{ T}\;+\;v\;(\cos(u+\varphi ),\sin(u+\varphi ),1)^{T}$

har två horisontella cirklar som riktlinjer. Den extra parametern $\varphi$ tillåter att variera de parametriska representationerna av cirklarna. För

$\varphi =0\$ man får cylindern $x^{2}+y^{2}=1$ , för

$\ varphi =\pi /2\$ får man konen $x^{2}+y^{2}=z^{2}$ och för

${ \displaystyle 0<\varphi <\pi /2\ }$ man får en hyperboloid av ett ark med ekvation $\ {\tfrac {x^{2}+ y^{2}}{a^{2}}}-{\tfrac {z^{2}}{c^{2}}}=1\$ och halvaxlarna $\ a=\cos \varphi \;,\;c=\cot \varphi$ .

En hyperboloid av ett ark är en dubbelt reglad yta.

Hyperbolisk paraboloid

Hyperbolisk paraboloid

Huvudartikel: Hyperbolisk paraboloid

Om de två direktlinjerna i (CD) är linjerna

$\mathbf {c} (u)=(1-u) \mathbf {a} _{1}+u\mathbf {a} _{2},\quad \mathbf {d} (u)=(1-u)\mathbf {b} _{1}+u\mathbf {b} _{2}$

man får

$\mathbf {x} (u ,v)=(1-v){\big (}(1-u)\mathbf {a} _{1}+u\mathbf {a} _{2}{\big )}\ +\ v{\ stor (}(1-u)\mathbf {b} _{1}+u\mathbf {b} _{2}{\big )}\$ ,

vilket är den hyperboliska paraboloiden som interpolerar de fyra punkterna $\ \mathbf {a} _{1},\;\mathbf {a} _{2},\;\ mathbf {b} _{1},\;\mathbf {b} _{2}\$ bilinjärt.

Uppenbarligen är den härskade ytan en dubbelstyrd yta , eftersom vilken punkt som helst ligger på två linjer av ytan.

För exemplet som visas i diagrammet:

$\ \mathbf {a} _ {1}=(0,0,0)^{T},\;\mathbf {a} _{2}=(1,0,0)^{T},\;\mathbf {b} _{1 }=(0,1,0)^{T},\;\mathbf {b} _{2}=(1,1,1)^{T}\$ .

Den hyperboliska paraboloiden har ekvationen $z=xy$ .

Möbiusremsa

Möbiusremsa

Huvudartikel: Möbiusremsa

Den härskade ytan

$\mathbf {x} (u,v)=\mathbf {c} (u)+v\;\mathbf {r} (u )$

med

${\displaystyle \mathbf {c} (u)=(\cos 2u,\sin 2u,0)^{T}\ } ($ ringa in som directrix),

$\mathbf {r} (u)=(\ cos u\cos 2u,\cos u\sin 2u,\sin u)^{T}\ ,\quad 0\leq u<\pi \ ,$

innehåller en Möbiusremsa.

Diagrammet visar Möbius-remsan för $-0,3\leq v\leq 0,3$ .

En enkel beräkning visar ${\displaystyle \det(\mathbf {\dot {c}} (0)\;,\;\mathbf {\dot { r}} (0)\;,\;\mathbf {r} (0))\;\neq \;0\ } ($ se nästa avsnitt). Den givna realiseringen av en Möbiusremsa är därför inte framkallningsbar . Men det finns utvecklingsbara Möbius-remsor.

Ytterligare exempel

• Conoid
• Katalansk yta
• Framkallbara rullar ( oloid , sfärikon )

Tangentplan, framkallningsbara ytor

Av övervägandena nedan antas alla nödvändiga derivat föreligga.

För bestämning av normalvektorn i en punkt behöver man partialderivatorna av representationen $\quad \mathbf {x} (u,v) =\mathbf {c} (u)+v\;\mathbf {r} (u)$ :

$\mathbf {x} _{u}=\mathbf {\dot {c}} (u)+v\;\mathbf {\dot { r}} (u)\$ , $\quad \mathbf {x} _{v}=\;\mathbf {r} (u)$

Därför är normalvektorn

• $\mathbf {n} =\mathbf {x} _{u}\times \mathbf {x} _{v}=\mathbf {\dot {c}} \times \mathbf {r} +v(\ mathbf {\dot {r}} \times \mathbf {r} )\ .$

På grund av $\mathbf {n} \cdot \mathbf {r} =0$ (En blandad produkt med två lika vektorer är alltid 0 !), vektor $\mathbf {r } (u_{0})$ är en tangentvektor i vilken punkt som helst $\mathbf {x} (u_{0},v)$ . Tangentplanen längs denna linje är alla lika, om $\mathbf {\dot {r}} \times \mathbf {r}$ är en multipel av $\mathbf { \dot {c}} \times \mathbf {r}$ . Detta är endast möjligt om de tre vektorerna $\mathbf {\dot {c}} \;,\;\mathbf {\dot {r}} \;,\;\mathbf { r} \$ ligger i ett plan, dvs de är linjärt beroende. Det linjära beroendet av tre vektorer kan kontrolleras med determinanten för dessa vektorer:

• Tangentplanen längs linjen $\mathbf {x} (u_{0},v)=\mathbf {c} (u_{0} )+v\;\mathbf {r} (u_{0})$ är lika, om

$\det(\mathbf {\dot {c}} (u_{0})\;,\;\mathbf {\dot {r}} (u_{0})\;,\;\mathbf {r } (u_{0}))\;=\;0\ .$

Vikten av detta determinant tillstånd visar följande uttalande:

• En styrd yta $\quad \mathbf {x} (u,v)=\mathbf {c} (u)+v\;\mathbf {r} (u)$ kan utvecklas till ett plan, om Gauss-kurvaturen försvinner för någon punkt. Detta är exakt fallet om

$\det(\mathbf {\dot {c}} \;,\;\mathbf {\dot {r}} \;,\ ;\mathbf {r} )\;=\;0\quad$

när som helst är sant.

Generatorerna av en styrd yta sammansmälter med en familj av dess asymptotiska linjer. För framkallningsbara ytor utgör de också en familj av dess krökningslinjer . Det kan visas att vilken framkallningsbar yta som helst är en kon, en cylinder eller en yta som bildas av alla tangenter i en rymdkurva.

Applicering och historia av framkallningsbara ytor

Utvecklabar koppling av två ellipser och dess utveckling

Det determinanta villkoret för framkallningsbara ytor används för att bestämma numeriskt framkallbara samband mellan rymdkurvor (riktlinjer). Diagrammet visar en framkallningsbar koppling mellan två ellipser i olika plan (en horisontell, den andra vertikal) och dess utveckling.

Ett intryck av användningen av framkallbara ytor inom datorstödd design ( CAD ) ges i interaktiv design av framkallbara ytor

En historisk översikt över framkallningsbara ytor finns i Framkallbara ytor: deras historia och tillämpning

Styrda ytor i algebraisk geometri

Huvudartikel: Reglerad sort

I algebraisk geometri definierades härskade ytor ursprungligen som projektiva ytor i projektivt utrymme innehållande en rät linje genom någon given punkt. Detta innebär omedelbart att det finns en projektiv linje på ytan genom en given punkt, och detta tillstånd används nu ofta som definitionen av en reglerad yta: reglerade ytor definieras som abstrakta projektiva ytor som uppfyller detta villkor att det finns en projektiv linje genom vilken punkt som helst. Detta motsvarar att säga att de är birational till produkten av en kurva och en projektiv linje. Ibland definieras en reglerad yta som en som uppfyller det starkare villkoret att den har en fibrering över en kurva med fibrer som är projektiva linjer. Detta utesluter det projektiva planet, som har en projektiv linje genom varje punkt men inte kan skrivas som en sådan fibrering.

Reglade ytor förekommer i Enriques klassificering av projektiva komplexa ytor, eftersom varje algebraisk yta av Kodaira-dimensionen $-\infty$ är en reglerad yta (eller ett projektivt plan, om man använder den restriktiva definitionen av reglerad yta). Varje minimal projektiv styrd yta förutom det projektiva planet är det projektiva knippet av ett 2-dimensionellt vektorknippe över någon kurva. De styrda ytorna med baskurva av släktet 0 är Hirzebruch-ytorna .

Styrda ytor i arkitektur

Dubbelstyrda ytor är inspirationen till krökta hyperboloida strukturer som kan byggas med ett gallerverk av raka element, nämligen:

• Hyperboliska paraboloider, såsom sadeltak .
• Hyperboloider av ett ark, som kyltorn och några papperskorgar .

RM -81 Agena- raketmotorn använde raka kylkanaler som lades ut i en reglerad yta för att bilda munstyckssektionens hals .

• 

  Kylning av hyperboliska torn vid Didcot Power Station , Storbritannien; ytan kan styras dubbelt.

• 

  Dubbelstyrt vattentorn med toroidformad tank, av Jan Bogusławski i Ciechanów , Polen

• 

  En hyperboloid Kobe Port Tower , Kobe , Japan, med dubbelt utslag.

• 

  Hyperboloid vattentorn, 1896 i Nizhny Novgorod .

• 

  Gallerskalet i Shukhov Tower i Moskva, vars sektioner är dubbelstyrda .

• 

  En styrd spiraltrappa inne i Cremonas Torrazzo .

• 

  Bykyrka i Selo, Slovenien: både taket (koniskt) och väggen (cylindrisk) är styrda ytor.

• 

  Ett hyperboliskt paraboloidtak på Warszawa Ochota järnvägsstation i Warszawa , Polen.

• 

  En härdat konisk hatt .

• 

  Korrugerade takpannor styrda av parallella linjer i en riktning och sinusformade i vinkelrät riktning

• 

  Konstruktion av en plan yta genom härdande ( avjämning ) betong

•   Do Carmo, Manfredo P.: Differentialgeometri för kurvor och ytor , Prentice-Hall; 1 upplaga, 1976 ISBN 978-0132125895
•    Barth, Wolf P.; Hulek, Klaus; Peters, Chris AM; Van de Ven, Antonius (2004), Compact Complex Surfaces , Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge., vol. 4, Springer-Verlag, Berlin, doi : 10.1007/978-3-642-57739-0 , ISBN 978-3-540-00832-3 , MR 2030225
•    Beauville, Arnaud (1996), Komplexa algebraiska ytor , London Mathematical Society Student Texts, vol. 34 (2nd ed.), Cambridge University Press , doi : 10.1017/CBO9780511623936 , ISBN 978-0-521-49510-3 , MR 1406314
• Edge, WL (1931), The Theory of Ruled Surfaces , Cambridge University Press – via Internet Archive . Recension: Bulletin of the American Mathematical Society 37 (1931), 791-793, doi : 10.1090/S0002-9904-1931-05248-4
•   Fuchs, D.; Tabachnikov, Serge (2007), "16.5 Det finns inga icke-plana trippelstyrda ytor", Mathematical Omnibus: Thirty Lectures on Classic Mathematics , American Mathematical Society, sid. 228, ISBN 9780821843161 .
•   Li, Ta-chʻien (red.) (2011), Problems and Solutions in Mathematics, 3103 (2nd ed.), World Scientific Publishing Company , ISBN 9789810234805 {{ citation }} : |first= har ett generiskt namn ( hjälp ) .
•   Hilbert, David ; Cohn-Vossen, Stephan (1952), Geometry and the Imagination (2nd ed.), New York: Chelsea, ISBN 978-0-8284-1087-8 .
• Iskovskikh, VA (2001) [1994], "Ruled yta" , Encyclopedia of Mathematics , EMS Press
•   Sharp, John (2008), D-Forms: överraskande nya 3D-former från platta böjda former , Tarquin, ISBN 978-1-899618-87-3 . Recension: Séquin, Carlo H. (2009), Journal of Mathematics and the Arts 3: 229–230, doi : 10.1080/17513470903332913

externa länkar

• Weisstein, Eric W. "Ruled Surface" . MathWorld .
• Regerade ytbilder från University of Arizona
• Exempel på framkallningsbara ytor på webbplatsen Rhino3DE