Katalansk yta

Den här artikeln handlar om de styrda ytorna. För den minimala ytan, se Katalanska minimala ytan .

En katalansk yta.

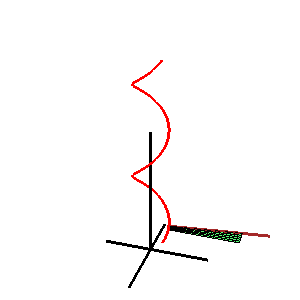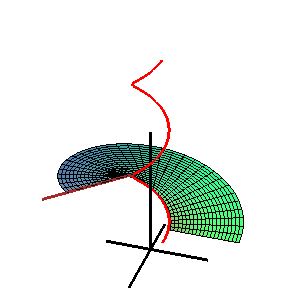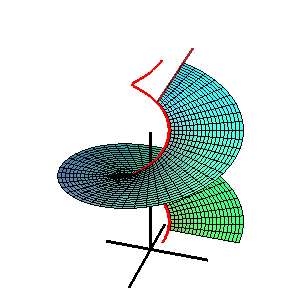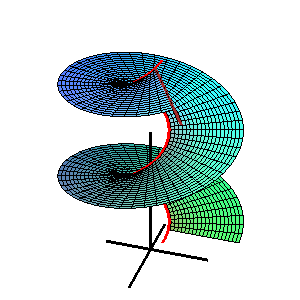
Inom geometrin är en katalansk yta , uppkallad efter den belgiske matematikern Eugène Charles Catalan , en styrd yta vars alla utslag är parallella med ett fast plan .

Ekvationer

Vektorekvationen för en katalansk yta ges av

r = s ( u ) + v L ( u ),

där r = s ( u ) är rymdkurvan och L ( u ) är enhetsvektorn för regeln vid u = u . Alla vektorerna L ( u ) är parallella med samma plan, som kallas ytans riktningsplan . Detta kan karakteriseras av villkoret: den blandade produkten [ L ( u ), L' ( u ), L" ( u )] = 0. [1]

De parametriska ekvationerna för den katalanska ytan är [2]

$x=f(u)+vi( u),\quad y=g(u)+vj(u),\quad z=h(u)+vk(u)\,$

Speciella fall

Om alla härskar för en katalansk yta skär en fast linje , så kallas ytan en konoid .

Katalanska bevisade att helicoiden och planet var de enda styrda minimala ytorna .

Se även

• Generaliserad helicoid

•   A. Gray, E. Abbena, S. Salamon, Modern differentialgeometri av kurvor och ytor med Mathematica , 3:e uppl. Boca Raton, Florida:CRC Press, 2006. [3] ( ISBN 978-1-58488-448-4 )
• "Catalan surface" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
•   VY Rovenskii, Geometri av kurvor och ytor med LÖNN [4] ( ISBN 978-0-8176-4074-3 )