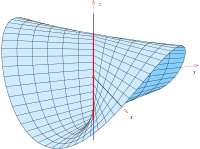
Conoid

För organellen som kallas konoid som används av intracellulära parasiter , se myzocytos .

Höger cirkulär konoid:

 Directrix är en cirkel

  Axeln är vinkelrät mot   riktningsplanet

I geometri är en konoid (från grekiska κωνος 'kon' och - ειδης 'liknande') en reglerad yta , vars utslag (linjer) uppfyller de ytterligare villkoren:

(1) Alla utslag är parallella med ett plan . , riktningsplanet

(2) Alla domslut skär en fast linje, axeln .

Konoiden är en höger konoid om dess axel är vinkelrät mot dess riktlinjeplan. Därför är alla utslag vinkelräta mot axeln.

På grund av (1) är vilken konoid som helst en katalansk yta och kan representeras parametriskt av

$\mathbf {x} (u,v)=\mathbf {c} (u)+v\mathbf {r} (u)\$

Valfri kurva ₀ x ( u , v ) med fast parameter u = u ₀ är en regel, c ( u ) beskriver riktningen och vektorerna r ( u ) är alla parallella med riktningsplanet. Planariteten hos vektorerna r ( u ) kan representeras av

$\det(\mathbf {r} ,\mathbf {\dot {r}} ,\mathbf {\ddot {r}} )=0$ .

Om riktningen är en cirkel, kallas konoiden en cirkulär konoid .

Termen conoid användes redan av Arkimedes i hans avhandling On Conoids and Spheroides .

Exempel

Höger cirkulär konoid

Den parametriska representationen

$\mathbf {x} (u,v )=(\cos u,\sin u,0)+v(0,-\sin u,z_{0})\ ,\ 0\leq u<2\pi ,v\in \mathbb {R}$

beskriver en rät cirkulär konoid med enhetscirkeln för xy-planet som riktlinje och ett riktlinjeplan, som är parallellt med y--z-planet. Dess axel är linjen $(x,0,z_{0})\ x\in \mathbb {R} \ .$

Specialfunktioner :

1. Skärningen med ett horisontellt plan är en ellips.
2. $(1-x^{2})(z-z_{0})^{2}-y^{2}z_{ 0}^{2}=0$ är en implicit representation. Därför är den högra cirkulära konoiden en yta av grad 4.
3. Keplers regel ger för en rät cirkulär konoid med radie $r$ och höjd $h$ den exakta volymen: $V={\tfrac {\pi }{2} }r^{2}h$ .

också av punkterna på linjen ${\displaystyle (x,0,z_{0})} .$ För dessa punkter finns det inga tangentplan . Sådana punkter kallas singular .

Parabolisk konoid

parabolisk konoid: directrix är en parabel

Den parametriska representationen

$\mathbf {x} (u,v)=\left(1,u,-u^ {2}\right)+v\left(-1,0,u^{2}\right)$

${ \displaystyle =\left(1-v,u,-(1-v)u^{2}\right)\ ,u,v\in \mathbb {R} \ ,}$

beskriver en parabolisk konoid med ekvationen $z=-xy^{2}$ . Konoiden har en parabel som riktlinje, y-axeln som axel och ett plan parallellt med xz-planet som riktningsplan. Den används av arkitekter som takyta (s. nedan).

Den paraboliska konoiden har inga singulära punkter.

Ytterligare exempel

1. hyperbolisk paraboloid
2. Plücker konoid
3. Whitney paraply
4. helikoid

• 

  hyperbolisk paraboloid

• 

  Plücker konoid

• 

  Whitney paraply

Ansökningar

konoid i arkitektur

konoider i arkitektur

Matematik

Det finns många konoider med singulära punkter, som undersöks i algebraisk geometri .

Arkitektur

Liksom andra styrda ytor är konoider av stort intresse för arkitekter, eftersom de kan byggas med balkar eller stänger. Höger konoider kan enkelt tillverkas: man trär stänger på en axel så att de bara kan roteras runt denna axel. Efteråt böjer man bort stängerna med en riktlinje och genererar en konoid (s. parabolisk konoid).

externa länkar

• mathworld: Plücker conoid
• "Conoid" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]

•   A. Gray, E. Abbena, S. Salamon, Modern differentialgeometri av kurvor och ytor med Mathematica, 3:e uppl. Boca Raton, FL:CRC Press, 2006. [1] ( ISBN 978-1-58488-448-4 )
•   Vladimir Y. Rovenskii, Geometri av kurvor och ytor med LÖNN [2] ( ISBN 978-0-8176-4074-3 )