Plancks lag
Inom fysiken beskriver Plancks lag den spektrala tätheten av elektromagnetisk strålning som sänds ut av en svart kropp i termisk jämvikt vid en given temperatur T , när det inte finns något nettoflöde av materia eller energi mellan kroppen och dess miljö.
I slutet av 1800-talet kunde fysiker inte förklara varför det observerade spektrumet av svartkroppsstrålning, som då hade mätts noggrant, avviker betydligt vid högre frekvenser från det som förutspåtts av befintliga teorier. År 1900 härledde den tyske fysikern Max Planck heuristiskt en formel för det observerade spektrumet genom att anta att en hypotetisk elektriskt laddad oscillator i en hålighet som innehöll strålning från svartkroppen endast kunde ändra sin energi i ett minimalt steg, E , som var proportionell mot frekvensen av dess tillhörande elektromagnetiska våg . [ inkonsekvent ] Detta löste problemet med den ultravioletta katastrofen som förutspåtts av klassisk fysik . Denna upptäckt var en banbrytande insikt i modern fysik och är av grundläggande betydelse för kvantteorin .
Lagen
Varje fysisk kropp avger spontant och kontinuerligt elektromagnetisk strålning och en kropps spektrala strålning , B , beskriver den spektrala emissionseffekten per ytenhet, per enhet rymdvinkel, per enhet frekvens för speciella strålningsfrekvenser. Relationen som ges av Plancks strålningslag, som ges nedan, visar att med ökande temperatur ökar den totala utstrålade energin från en kropp och toppen av det emitterade spektrumet skiftar till kortare våglängder. Enligt detta ges spektralstrålningen för en kropp för frekvensen ν vid absolut temperatur T av
Likställande av integralen av spektral strålning per våglängdsenhet med integralen av per enhet frekvens
Genom att använda ser vi att
visar hur utstrålad energi som sänds ut vid kortare våglängder ökar snabbare med temperaturen än energi som sänds ut vid längre våglängder. Lagen kan också uttryckas i andra termer, såsom antalet fotoner som emitteras vid en viss våglängd, eller energitätheten i en strålningsvolym. SI- enheterna för B ν är W · sr −1 · m −2 · Hz −1 , medan de för B λ är W·sr −1 ·m −3 .
I gränsen för låga frekvenser (dvs. långa våglängder) tenderar Plancks lag till Rayleigh-Jeans lag , medan den i gränsen för höga frekvenser (dvs. små våglängder) tenderar till Wien-approximationen .
Max Planck utvecklade lagen 1900 med endast empiriskt bestämda konstanter, och visade senare att det, uttryckt som en energifördelning, är den unika stabila fördelningen för strålning i termodynamisk jämvikt . Som en energifördelning är den en av en familj av termiska jämviktsfördelningar som inkluderar Bose-Einstein-fördelningen , Fermi -Dirac-fördelningen och Maxwell-Boltzmann-fördelningen .
Svartkroppsstrålning
En svartkropp är ett idealiserat objekt som absorberar och avger alla strålningsfrekvenser. Nära termodynamisk jämvikt , är den emitterade strålningen närmare beskriven av Plancks lag och på grund av dess beroende av temperatur , sägs Planck-strålning vara termisk strålning, så att ju högre temperatur en kropp är desto mer strålning sänder den ut vid varje våglängd.
Planckstrålning har en maximal intensitet vid en våglängd som beror på kroppens temperatur. Till exempel, vid rumstemperatur (~ 300 K ), avger en kropp termisk strålning som mestadels är infraröd och osynlig. Vid högre temperaturer ökar mängden infraröd strålning och kan kännas som värme, och mer synlig strålning sänds ut så att kroppen lyser synligt rött. Vid högre temperaturer är kroppen ljusgul eller blåvit och avger betydande mängder kortvågsstrålning, inklusive ultraviolett och till och med röntgenstrålar . Solens yta (~ 6000 K ) avger stora mängder både infraröd och ultraviolett strålning; dess emission är en topp i det synliga spektrumet. Denna förskjutning på grund av temperatur kallas Wiens förskjutningslag .
Planckstrålning är den största mängden strålning som någon kropp vid termisk jämvikt kan avge från sin yta, oavsett dess kemiska sammansättning eller ytstruktur. Strålningens passage över ett gränssnitt mellan media kan karakteriseras av gränssnittets emissivitet (förhållandet mellan den faktiska strålningen och den teoretiska Planck-strålningen), vanligtvis betecknad med symbolen ε . Det är i allmänhet beroende av kemisk sammansättning och fysisk struktur, på temperatur, på våglängden, på passagevinkeln och på polarisationen . Emissiviteten för ett naturligt gränssnitt är alltid mellan ε = 0 och 1.
En kropp som gränsar till ett annat medium som både har ε = 1 och absorberar all strålning som infaller på det, sägs vara en svart kropp. Ytan på en svart kropp kan modelleras av ett litet hål i väggen på ett stort hölje som hålls vid en enhetlig temperatur med ogenomskinliga väggar som, vid varje våglängd, inte är perfekt reflekterande. Vid jämvikt beskrivs strålningen inuti denna inneslutning av Plancks lag, liksom strålningen som lämnar det lilla hålet.
Precis som Maxwell-Boltzmann-fördelningen är den unika maximala entropienergifördelningen för en gas av materialpartiklar vid termisk jämvikt, så är Plancks fördelning för en gas av fotoner . Till skillnad från en materialgas där massorna och antalet partiklar spelar en roll, bestäms den spektrala strålningen, trycket och energitätheten för en fotongas vid termisk jämvikt helt av temperaturen.
Om fotongasen inte är planckisk, garanterar termodynamikens andra lag att interaktioner (mellan fotoner och andra partiklar eller till och med, vid tillräckligt höga temperaturer, mellan fotonerna själva) kommer att få fotonenergifördelningen att förändras och närma sig Planckfördelningen. I ett sådant tillvägagångssätt för termodynamisk jämvikt skapas eller förintas fotoner i rätt antal och med rätt energier för att fylla kaviteten med en Planckfördelning tills de når jämviktstemperaturen. Det är som om gasen är en blandning av sub-gaser, en för varje band av våglängder, och varje sub-gas når så småningom den vanliga temperaturen.
Storheten B ν ( ν , T ) är den spektrala radiansen som funktion av temperatur och frekvens. Den har enheterna W · m −2 · sr −1 · Hz −1 i SI-systemet . En oändlig mängd effekt B ν ( ν , T ) cos θ dA d Ω dν utstrålas i den riktning som beskrivs av vinkeln θ från ytnormalen från infinitesimal ytarea dA till infinitesimal rymdvinkel d Ω i ett oändligt frekvensband av bredd dν centrerad på frekvensen ν . Den totala effekten som utstrålas in i en rymdvinkel är integralen av B ν ( ν , T ) över dessa tre kvantiteter, och ges av Stefan–Boltzmanns lag . Den spektrala utstrålningen av planckisk strålning från en svart kropp har samma värde för varje riktning och vinkel av polarisationen, och så sägs den svarta kroppen vara en lambertiansk radiator .
Olika former
Plancks lag kan förekomma i flera former beroende på olika vetenskapsområdens konventioner och preferenser. De olika formerna av lagen för spektral strålning sammanfattas i tabellen nedan. Former till vänster påträffas oftast i experimentfält , medan de till höger oftast påträffas i teoretiska fält .
| med h | med ħ | ||
|---|---|---|---|
| variabel | distribution | variabel | distribution |
|
Frekvens ν |
Vinkelfrekvens ω |
||
|
Våglängd λ |
Vinkelvåglängd y |
||
|
Vågnummer ν̃ |
Vinkelvågnummer k |
||
Dessa fördelningar representerar den spektrala radiansen för svarta kroppar – kraften som emitteras från den emitterande ytan, per enhet projicerad area av emitterande yta, per enhet rymdvinkel , per spektralenhet (frekvens, våglängd, vågnummer eller deras vinkelekvivalenter). Eftersom strålningen är isotrop (dvs. oberoende av riktning), är kraften som sänds ut i en vinkel mot det normala proportionell mot den projicerade ytan och därför mot cosinus för den vinkeln enligt Lamberts cosinuslag , och är opolariserad .
Överensstämmelse mellan spektrala variabla former
Olika spektrala variabler kräver olika motsvarande uttrycksformer för lagen. I allmänhet får man inte konvertera mellan de olika formerna av Plancks lag bara genom att ersätta en variabel med en annan, eftersom detta inte skulle ta hänsyn till att de olika formerna har olika enheter. Våglängds- och frekvensenheter är ömsesidiga.
Motsvarande uttrycksformer är relaterade eftersom de uttrycker ett och samma fysiska faktum: för ett visst fysiskt spektralt inkrement utstrålas ett motsvarande speciellt fysiskt energitillskott.
Detta gäller oavsett om det uttrycks i termer av en ökning av frekvensen, d ν , eller, på motsvarande sätt, av våglängden, d λ . Införande av ett minustecken kan indikera att en ökning av frekvensen motsvarar en minskning av våglängden. För att konvertera motsvarande former så att de uttrycker samma kvantitet i samma enheter multiplicerar vi med det spektrala inkrementet. Sedan, för ett speciellt spektralt inkrement, kan det särskilda fysiska energitillskottet skrivas
Dessutom är ν ( λ ) = c / λ , så att dν / dλ = − c / λ 2 . Substitution ger överensstämmelsen mellan frekvens- och våglängdsformerna, med deras olika dimensioner och enheter. Följaktligen,
Uppenbarligen beror platsen för toppen av spektralfördelningen för Plancks lag på valet av spektral variabel. Ändå, på ett sätt att säga, betyder denna formel att formen på spektralfördelningen är oberoende av temperatur, enligt Wiens förskjutningslag, som beskrivs nedan i underavsnittet Percentiler i avsnittet Egenskaper .
Spektral energitäthetsform
Plancks lag kan också skrivas i termer av den spektrala energitätheten ( u ) genom att multiplicera B med 4π / c :
Dessa fördelningar har energienheter per volym per spektralenhet.
Första och andra strålningskonstanter
I ovanstående varianter av Plancks lag använder våglängds- och vågnummervarianterna termerna 2 hc 2 och hc / k B som endast omfattar fysikaliska konstanter. Följaktligen kan dessa termer betraktas som fysikaliska konstanter i sig och kallas därför för den första strålningskonstanten c 1 L och den andra strålningskonstanten c 2 med
och
Med hjälp av strålningskonstanterna kan våglängdsvarianten av Plancks lag förenklas till
L används här istället för B eftersom det är SI-symbolen för spektral radians . L i c 1 L hänvisar till det . Denna referens är nödvändig eftersom Plancks lag kan omformuleras för att ge spektral strålningsexitans M ( λ , T ) snarare än spektral radians L ( λ , T ) , i vilket fall c 1 ersätter c 1 L , med
så att Plancks lag för spektral strålningsexitans kan skrivas som
I takt med att mätteknikerna har förbättrats har generalkonferensen om vikter och mått reviderat sin uppskattning av c 2 ; se Planckian locus § Internationell temperaturskala för detaljer.
Fysik
Plancks lag beskriver den unika och karakteristiska spektralfördelningen för elektromagnetisk strålning i termodynamisk jämvikt, när det inte finns något nettoflöde av materia eller energi. Dess fysik är lättast att förstå genom att betrakta strålningen i en hålighet med stela ogenomskinliga väggar. Väggarnas rörelser kan påverka strålningen. Om väggarna inte är ogenomskinliga, är den termodynamiska jämvikten inte isolerad. Det är av intresse att förklara hur den termodynamiska jämvikten uppnås. Det finns två huvudfall: (a) när inställningen till termodynamisk jämvikt sker i närvaro av materia, när hålrummets väggar är ofullkomligt reflekterande för varje våglängd eller när väggarna är perfekt reflekterande medan hålrummet innehåller en liten svart kropp ( detta var huvudfallet som Planck övervägde); eller (b) när inställningen till jämvikt sker i frånvaro av materia, när väggarna är perfekt reflekterande för alla våglängder och kaviteten inte innehåller någon materia. För materia som inte är innesluten i en sådan kavitet kan värmestrålning ungefär förklaras genom lämplig användning av Plancks lag.
Klassisk fysik ledde, via equipartition theorem , till den ultravioletta katastrofen , en förutsägelse att den totala svartkroppsstrålningsintensiteten var oändlig. Om den kompletteras med det klassiskt oförsvarliga antagandet att strålningen av någon anledning är ändlig, ger klassisk termodynamik en redogörelse för vissa aspekter av Planck-fördelningen, såsom Stefan– Boltzmann-lagen och Wiens förskjutningslag . För fallet med närvaron av materia ger kvantmekaniken en bra redogörelse, som finns nedan i avsnittet med rubriken Einstein-koefficienter . Detta ansågs av Einstein och används numera för kvantoptik. För fallet av frånvaro av materia är kvantfältteori nödvändig, eftersom icke-relativistisk kvantmekanik med fasta partikelantal inte ger en tillräcklig redogörelse.
Fotoner
Kvantteoretisk förklaring av Plancks lag ser strålningen som en gas av masslösa, oladdade, bosoniska partiklar, nämligen fotoner, i termodynamisk jämvikt . Fotoner ses som bärare av den elektromagnetiska interaktionen mellan elektriskt laddade elementarpartiklar. Fotonnummer bevaras inte. Fotoner skapas eller förintas i rätt antal och med rätt energier för att fylla håligheten med Planck-fördelningen. För en fotongas i termodynamisk jämvikt bestäms den inre energitätheten helt av temperaturen; dessutom bestäms trycket helt av den inre energitätheten. Detta är till skillnad från fallet med termodynamisk jämvikt för materialgaser, för vilka den inre energin inte bara bestäms av temperaturen, utan också oberoende av de olika molekylernas respektive antal och återigen oberoende av de olika egenskaperna hos de olika molekylerna. molekyler. För olika materialgaser vid given temperatur kan trycket och den inre energitätheten variera oberoende av varandra, eftersom olika molekyler oberoende kan bära olika excitationsenergier.
Plancks lag uppstår som en gräns för Bose–Einstein-fördelningen , energifördelningen som beskriver icke-interaktiva bosoner i termodynamisk jämvikt. I fallet med masslösa bosoner som fotoner och gluoner är den kemiska potentialen noll och Bose-Einstein-fördelningen minskar till Planck-fördelningen. Det finns en annan grundläggande jämviktsenergifördelning: Fermi-Dirac-fördelningen , som beskriver fermioner , såsom elektroner, i termisk jämvikt. De två fördelningarna skiljer sig åt eftersom flera bosoner kan uppta samma kvanttillstånd, medan flera fermioner inte kan. Vid låga densiteter är antalet tillgängliga kvanttillstånd per partikel stort, och denna skillnad blir irrelevant. I lågdensitetsgränsen minskar Bose-Einstein- och Fermi-Dirac-fördelningen var och en till Maxwell-Boltzmann-fördelningen .
Kirchhoffs lag om termisk strålning
Kirchhoffs lag om termisk strålning är en kortfattad och kortfattad redogörelse för en komplicerad fysisk situation. Följande är en inledande skiss av den situationen, och är mycket långt ifrån ett rigoröst fysiskt argument. Syftet här är bara att sammanfatta de huvudsakliga fysiska faktorerna i situationen och de viktigaste slutsatserna.
Spektralt beroende av termisk strålning
Det är skillnad på ledande värmeöverföring och strålningsvärmeöverföring . Strålningsvärmeöverföring kan filtreras för att passera endast ett bestämt band av strålningsfrekvenser.
Det är allmänt känt att ju varmare en kropp blir, desto mer värme strålar den ut vid varje frekvens.
I en kavitet i en ogenomskinlig kropp med stela väggar som inte är perfekt reflekterande vid någon frekvens, i termodynamisk jämvikt, finns det bara en temperatur, och den måste delas gemensamt av strålningen från varje frekvens.
Man kan föreställa sig två sådana kaviteter, var och en i sin egen isolerade strålnings- och termodynamiska jämvikt. Man kan föreställa sig en optisk anordning som tillåter strålningsvärmeöverföring mellan de två kaviteterna, filtrerad för att bara passera ett bestämt band av strålningsfrekvenser. Om värdena på de spektrala strålningarna för strålningarna i hålrummen skiljer sig i det frekvensbandet kan värme förväntas passera från det varmare till det kallare. Man skulle kunna föreslå att använda en sådan filtrerad värmeöverföring i ett sådant band för att driva en värmemotor. Om de två kropparna har samma temperatur tillåter termodynamikens andra lag inte att värmemotorn fungerar. Man kan dra slutsatsen att för en temperatur som är gemensam för de två kropparna måste värdena för de spektrala radianserna i passbandet också vara gemensamma. Detta måste gälla för varje frekvensband. Detta blev tydligt för Balfour Stewart och senare för Kirchhoff. Balfour Stewart fann experimentellt att av alla ytor avgav en av lampsvart den största mängden termisk strålning för varje strålningskvalitet, bedömd av olika filter.
Genom att tänka teoretiskt gick Kirchhoff lite längre och påpekade att detta innebar att den spektrala strålningen, som en funktion av strålningsfrekvensen, av en sådan kavitet i termodynamisk jämvikt måste vara en unik universell funktion av temperaturen. Han postulerade en idealisk svart kropp som samverkade med dess omgivningar på ett sådant sätt att den absorberar all strålning som faller på den. Enligt Helmholtz reciprocitetsprincip skulle strålning från det inre av en sådan kropp passera obehindrat, direkt till dess omgivningar utan reflektion vid gränsytan. I termodynamisk jämvikt skulle den termiska strålningen som emitteras från en sådan kropp ha den unika universella spektrala strålningen som en funktion av temperaturen. Denna insikt är roten till Kirchhoffs lag om termisk strålning.
Förhållandet mellan absorptionsförmåga och emissivitet
Man kan föreställa sig en liten homogen sfärisk materialkropp märkt X vid en temperatur TX , ett TY som ligger i strålningsfält i en stor hålighet med väggar av material märkta Y vid en temperatur . Kroppen X avger sin egen värmestrålning. Vid en viss frekvens ν kan strålningen som sänds ut från ett visst tvärsnitt genom X:s centrum I i ν , X ( T X ) en riktning i en riktning vinkelrät mot det tvärsnittet betecknas , karakteristiskt för materialet i X . Vid den frekvensen ν kan strålningseffekten från väggarna in i det tvärsnittet i motsatt mening i den riktningen betecknas TY I , ν , Y . TY ) för ( väggtemperaturen För materialet av X , definierar absorptionsförmågan α ν , X , Y ( T X , TY X ) som andelen av den infallande strålningen som absorberas av , absorberas den infallande energin med en hastighet α ν , X , Y ( T X ) , T Y ) I ν , Y ( T Y ) .
Hastigheten q ( ν , TX för , TY ackumulering ) av energi i en mening in i kroppens tvärsnitt kan sedan uttryckas
Kirchhoffs avgörande insikt, som nämndes precis ovan, var att det vid termodynamisk jämvikt vid temperatur T existerar en unik universell strålningsfördelning, numera betecknad B ν ( T ) , som är oberoende av de kemiska egenskaperna hos materialen X och Y , som leder till en mycket värdefull förståelse av strålningsutbytesjämvikten hos vilken kropp som helst, enligt följande.
När det råder termodynamisk jämvikt vid temperatur T har kavitetsstrålningen från väggarna det unika universella värdet, så att I ν , Y ( T Y ) = B ν ( T ) . Vidare kan man definiera emissiviteten ε ν , X ( T X ) I för ν , X ( T X ) = I ν , X ( T ) = ε ν , X ( T ) B ν ( T ) materialet i kroppen X just så att man vid termodynamisk jämvikt vid temperatur T X = T , har .
När termisk jämvikt råder vid temperatur q ( ν , T X , TY T ) = 0 = T X = T Y försvinner hastigheten för ackumulering av energi så att . Det följer att i termodynamisk jämvikt, när T = T X = T Y ,
Kirchhoff påpekade att det följer att i termodynamisk jämvikt, när T = T X = T Y ,
Genom att introducera den speciella notationen α ν , X ( T ) för absorptionsförmågan hos material X vid termodynamisk jämvikt vid temperatur T (motiverad av en upptäckt av Einstein, som indikeras nedan), har en ytterligare likheten
Likheten mellan absorptivitet och emissivitet som visas här är specifik för termodynamisk jämvikt vid temperatur T och förväntas i allmänhet inte hållas när förhållandena för termodynamisk jämvikt inte håller. Emissiviteten och absorptionsförmågan är var för sig egenskaper hos molekylerna i materialet men de beror på olika sätt på fördelningarna av tillstånden för molekylär excitation vid tillfället, på grund av ett fenomen som kallas "stimulerad emission", som upptäcktes av Einstein. Vid tillfällen när materialet är i termodynamisk jämvikt eller i ett tillstånd som kallas lokal termodynamisk jämvikt, blir emissiviteten och absorptionsförmågan lika. Mycket stark infallande strålning eller andra faktorer kan störa termodynamisk jämvikt eller lokal termodynamisk jämvikt. Lokal termodynamisk jämvikt i en gas innebär att molekylära kollisioner vida överväger ljusemission och absorption vid bestämning av fördelningarna av tillstånden för molekylär excitation.
Kirchhoff påpekade att han inte kände till den exakta karaktären av B ν ( T ) , men han ansåg att det var viktigt att det skulle redas ut. Fyra decennier efter Kirchhoffs insikt om de allmänna principerna för dess existens och karaktär var Plancks bidrag att bestämma det exakta matematiska uttrycket för den jämviktsfördelningen B ν ( T ) .
Svart kropp
Inom fysiken betraktar man en idealisk svart kropp, här märkt B , definierad som en som fullständigt absorberar all elektromagnetisk strålning som faller på den vid varje frekvens ν (därav termen "svart"). Enligt Kirchhoffs lag om värmestrålning innebär detta att man för varje frekvens ν , vid termodynamisk jämvikt vid temperatur T , har α ν , B ( T ) = ε ν , B ( T ) = 1 , så att värmestrålningen fr.o.m. en svart kropp är alltid lika med hela mängden som anges av Plancks lag. Ingen fysisk kropp kan sända ut värmestrålning som överstiger den från en svart kropp, eftersom om den var i jämvikt med ett strålningsfält, skulle den sända ut mer energi än vad som inföll på den.
Även om perfekt svarta material inte existerar, kan en svart yta i praktiken uppskattas exakt. När det gäller dess materiella inre är en kropp av kondenserad materia, flytande, fast eller plasma, med en bestämd gränsyta med omgivningen, helt svart för strålning om den är helt ogenomskinlig. Det betyder att den absorberar all strålning som tränger in i kroppens gränssnitt med dess omgivning och kommer in i kroppen. Detta är inte alltför svårt att uppnå i praktiken. Å andra sidan finns inte ett helt svart gränssnitt i naturen. Ett perfekt svart gränssnitt reflekterar ingen strålning, utan överför allt som faller på det, från båda sidor. Det bästa praktiska sättet att göra ett effektivt svart gränssnitt är att simulera ett "gränssnitt" av ett litet hål i väggen i ett stort hålrum i en helt ogenomskinlig styv kropp av material som inte reflekterar perfekt vid någon frekvens, med dess väggar vid en kontrollerad temperatur. Utöver dessa krav är komponentmaterialet i väggarna obegränsat. Strålning som kommer in i hålet har nästan ingen möjlighet att fly ur hålrummet utan att absorberas av flera stötar med dess väggar.
Lamberts cosinus lag
Som förklarat av Planck har en utstrålande kropp ett inre som består av materia och en gränsyta med dess angränsande angränsande materialmedium, vilket vanligtvis är det medium inifrån vilket strålningen från kroppens yta observeras. Gränssnittet är inte sammansatt av fysisk materia utan är en teoretisk uppfattning, en matematisk tvådimensionell yta, en gemensam egenskap hos de två sammanhängande medierna, som strängt taget inte hör till någondera separat. Ett sådant gränssnitt kan varken absorbera eller sända ut, eftersom det inte är sammansatt av fysisk materia; men det är platsen för reflektion och överföring av strålning, eftersom det är en yta av diskontinuitet av optiska egenskaper. Reflexionen och överföringen av strålning vid gränssnittet följer Stokes–Helmholtz ömsesidighetsprincipen .
När som helst i det inre av en svart kropp belägen inuti en kavitet i termodynamisk jämvikt vid temperatur T är strålningen homogen, isotrop och opolariserad. En svart kropp absorberar allt och reflekterar ingen av den elektromagnetiska strålningen som faller på den. Enligt Helmholtz reciprocitetsprincip reflekteras strålning från det inre av en svart kropp inte på dess yta, utan överförs helt till dess yttre. På grund av strålningens isotropi i kroppens inre är den spektrala strålningen av strålning som överförs från dess inre till dess yttre genom dess yta oberoende av riktning.
Detta uttrycks genom att säga att strålning från ytan av en svart kropp i termodynamisk jämvikt lyder Lamberts cosinus lag. Detta betyder att det spektrala flödet d Φ( dA , θ , d Ω, dν ) från ett givet infinitesimalt element av arean dA av den faktiska emitterande ytan av den svarta kroppen, detekterat från en given riktning som gör en vinkel θ med normalen till den faktiska emitterande ytan vid dA , in i ett element med rymd detekteringsvinkel d Ω centrerat på riktningen indikerad av θ , i ett element med frekvensbandbredd dν , kan representeras som
Faktorn cos θ är närvarande eftersom arean till vilken spektralstrålningen hänvisar direkt är projektionen av den faktiska emitterande ytarean på ett plan vinkelrätt mot riktningen indikerad av θ . Detta är anledningen till namnet cosinus lag .
Med hänsyn till riktningsoberoendet för den spektrala strålningen från strålningsytan på en svart kropp i termodynamisk jämvikt, har man 0 L ( dA , dν ) = B ν ( T ) och så
Således uttrycker Lamberts cosinus lag riktningsoberoendet för den spektrala radiansen B ν ( T ) på ytan av en svart kropp i termodynamisk jämvikt.
Stefan–Boltzmann lag
Den totala effekt som emitteras per ytenhet vid ytan av en svart kropp ( P ) kan hittas genom att integrera det svarta kroppsspektrala flödet från Lamberts lag över alla frekvenser, och över de rymdvinklar som motsvarar en halvklot ( h ) ovanför ytan .
Den oändliga rymdvinkeln kan uttryckas i sfäriska polära koordinater :
Så att:
Strålningsöverföring
Ekvationen för strålningsöverföring beskriver det sätt på vilket strålning påverkas när den färdas genom ett materialmedium. För det speciella fallet där materialmediet befinner sig i termodynamisk jämvikt i närheten av en punkt i mediet är Plancks lag av särskild betydelse.
För enkelhetens skull kan vi överväga det linjära stabila tillståndet, utan spridning . Ekvationen för strålningsöverföring anger att för en ljusstråle som går genom ett litet avstånd d s , bevaras energi: Förändringen i strålens (spektrala) strålning ( I ν ) är lika med mängden som avlägsnas av materialmediet plus mängden som erhålls från materialmediet. Om strålningsfältet är i jämvikt med materialmediet kommer dessa två bidrag att vara lika. Materialmediet kommer att ha en viss emissionskoefficient och absorptionskoefficient .
Absorptionskoefficienten α är den fraktionella förändringen i ljusstrålens intensitet när den färdas avståndet d s , och har längdenheter −1 . Den består av två delar, minskningen på grund av absorption och ökningen på grund av stimulerad emission . Stimulerad emission är emission från materialkroppen som orsakas av och är proportionell mot den inkommande strålningen. Den ingår i absorptionstermen eftersom den, liksom absorption, är proportionell mot intensiteten av den inkommande strålningen. Eftersom mängden absorption i allmänhet kommer att variera linjärt som materialets densitet ρ , kan vi definiera en "massabsorptionskoefficient" κ ν = α / ρ som är en egenskap hos själva materialet. Förändringen i intensitet hos en ljusstråle på grund av absorption när den korsar ett litet avstånd d s blir då
"Massemissionskoefficienten" j ν är lika med utstrålningen per volymenhet för ett element med liten volym dividerat med dess massa (eftersom, som för massabsorptionskoefficienten, emissionen är proportionell mot den emitterande massan) och har kraftenheter⋅ rymdvinkel −1 ⋅frekvens −1 ⋅densitet −1 . Liksom massabsorptionskoefficienten är den också en egenskap hos själva materialet. Förändringen i en ljusstråle när den korsar en liten sträcka d s blir då
Ekvationen för strålningsöverföring blir då summan av dessa två bidrag:
Om strålningsfältet är i jämvikt med materialmediet kommer strålningen att vara homogen (oberoende av position) så att dI ν = 0 och:
Einstein-koefficienter
Principen för detaljerad balans säger att vid termodynamisk jämvikt, balanseras varje elementär process av sin omvända process.
1916 tillämpade Albert Einstein denna princip på atomnivå på fallet med en atom som utstrålar och absorberar strålning på grund av övergångar mellan två specifika energinivåer, vilket gav en djupare insikt i ekvationen för strålningsöverföring och Kirchhoffs lag för denna typ av strålning. Om nivå 1 är den lägre energinivån med energi E 1 och nivå 2 är den övre energinivån med energi E 2 , så kommer frekvensen ν för strålningen som utstrålas eller absorberas att bestämmas av Bohrs frekvenstillstånd:
Om n 1 och n 2 är atomens antal densiteter i tillstånd 1 respektive 2, kommer hastigheten för förändring av dessa tätheter i tiden att bero på tre processer:
- Spontan emission
- Stimulerad emission
- Fotoabsorption
där u ν är strålningsfältets spektrala energitäthet. De tre parametrarna A 21 , B 21 och B 12 , kända som Einstein-koefficienterna, är associerade med fotonfrekvensen ν som produceras av övergången mellan två energinivåer (tillstånd). Som ett resultat har varje linje i ett spektra sin egen uppsättning associerade koefficienter. När atomerna och strålningsfältet är i jämvikt, kommer strålningen att ges av Plancks lag och, enligt principen om detaljerad balans, måste summan av dessa hastigheter vara noll:
Eftersom atomerna också är i jämvikt, är populationerna på de två nivåerna relaterade av Boltzmann-faktorn :
Dessa koefficienter gäller både atomer och molekyler.
Egenskaper
Toppar
Fördelningarna B ν , B ω , B ν̃ och B k toppar vid en fotonenergi av
Fördelningarna B λ och B ν toppar dock vid en annan energi
Anledningen till detta är att man, som nämnts ovan, inte kan gå från (till exempel) B ν till B λ genom att bara ersätta ν med λ . Dessutom måste man också multiplicera resultatet av substitutionen med
Denna 1 / λ 2 faktor flyttar fördelningens topp till högre energier. Dessa toppar är lägesenergin för en foton, när den lagras med användning av lika stora fack med frekvens respektive våglängd. Att dividera hc ( 14 387 .770 μm·K ) med dessa energiuttryck ger toppens våglängd.
Den spektrala strålningen vid dessa toppar ges av:
med och
med
Under tiden är den genomsnittliga energin för en foton från en svartkropp
Uppskattningar

I gränsen för låga frekvenser (dvs långa våglängder) blir Plancks lag Rayleigh–Jeans lag
eller
Strålningen ökar med kvadraten på frekvensen, vilket illustrerar den ultravioletta katastrofen . Inom gränsen för höga frekvenser (dvs små våglängder) tenderar Plancks lag till Wien-approximationen :
Båda approximationerna var kända för Planck innan han utvecklade sin lag. Han leddes av dessa två approximationer för att utveckla en lag som inkorporerade båda gränserna, vilket slutligen blev Plancks lag.
Percentiler
Det finns inget uttryck i sluten form för integralen av Planck-formeln mellan två våglängder, men det finns oändliga summauttryck .
Denna serie konvergerar inte för på grund av poler vid
Integralen över alla frekvenser är
Liknande serier finns för antalet fotoner per ytenhet per steradian:
| Percentil | λ T (μm·K) | λ k B T / hc |
|---|---|---|
| 0,01 % | 910 | 0,0632 |
| 0,1 % | 1110 | 0,0771 |
| 1 % | 1448 | 0,1006 |
| 10 % | 2195 | 0,1526 |
| 20 % | 2676 | 0,1860 |
| 25,0 % | 2898 | 0,2014 |
| 30 % | 3119 | 0,2168 |
| 40 % | 3582 | 0,2490 |
| 41,8 % | 3670 | 0,2551 |
| 50 % | 4107 | 0,2855 |
| 60 % | 4745 | 0,3298 |
| 64,6 % | 5099 | 0,3544 |
| 70 % | 5590 | 0,3885 |
| 80 % | 6864 | 0,4771 |
| 90 % | 9376 | 0,6517 |
| 99 % | 22884 | 1,5905 |
| 99,9 % | 51613 | 3,5873 |
| 99,99 % | 113374 | 7,8799 |
Wiens förskjutningslag i sin starkare form säger att formen på Plancks lag är oberoende av temperatur. Det är därför möjligt att lista den totala strålningens percentilpunkter samt topparna för våglängd och frekvens, i en form som ger våglängden λ dividerad med temperatur T . Den andra kolumnen i följande tabell listar motsvarande värden för λT , det vill säga de värden för x för vilka våglängden λ är x / T mikrometer vid radianspercentilpunkten som ges av motsvarande post i den första kolumnen.
Det vill säga, 0,01 % av strålningen har en våglängd under 910 / T µm, 20 % under 2676 / T µm , etc. Våglängds- och frekvenstopparna är i fet stil och uppträder vid 25,0 % respektive 64,6 %. Punkten på 41,8 % är den våglängds-frekvens-neutrala toppen (dvs. toppen i effekt per enhetsändring i logaritm för våglängd eller frekvens). Dessa är de punkter där respektive Planck-lagsfunktioner 1 / λ 5 , ν 3 och ν 2 / λ 2 , delat med exp ( hν / k B T ) − 1 uppnår sina maxima. Det mycket mindre gapet i förhållandet mellan våglängderna mellan 0,1 % och 0,01 % (1110 är 22 % mer än 910) än mellan 99,9 % och 99,99 % (113374 är 120 % mer än 51613) återspeglar den exponentiella avklingningen av energi vid kort våglängd slut) och polynomförfall vid lång tid.
Vilken topp som ska användas beror på applikationen. Det konventionella valet är våglängdstoppen vid 25,0 % som ges av Wiens förskjutningslag i dess svaga form. För vissa ändamål kan medianen eller 50 %-punkten som delar upp den totala strålningen i två halvor vara mer lämplig. Den senare är närmare frekvenstoppen än våglängdstoppen eftersom radiansen sjunker exponentiellt vid korta våglängder och endast polynomiellt vid långa. Den neutrala toppen inträffar vid en kortare våglängd än medianen av samma anledning.
| Percentil | Sol λ (µm) | Svart kropp på 5778K | 288 K planeten λ (µm) |
|---|---|---|---|
| 0,01 % | 0,203 | 0,157 | 3.16 |
| 0,1 % | 0,235 | 0,192 | 3,85 |
| 1 % | 0,296 | 0,251 | 5.03 |
| 10 % | 0,415 | 0,380 | 7,62 |
| 20 % | 0,484 | 0,463 | 9,29 |
| 25,0 % | 0,520 | 0,502 | 10.1 |
| 30 % | 0,556 | .540 | 10.8 |
| 41,8 % | 0,650 | 0,635 | 12.7 |
| 50 % | 0,727 | 0,711 | 14.3 |
| 60 % | 0,844 | 0,821 | 16.5 |
| 64,6 % | 0,911 | 0,882 | 17.7 |
| 70 % | 1,003 | 0,967 | 19.4 |
| 80 % | 1,242 | 1,188 | 23.8 |
| 90 % | 1,666 | 1,623 | 32.6 |
| 99 % | 3,728 | 3,961 | 79,5 |
| 99,9 % | 8,208 | 8,933 | 179 |
| 99,99 % | 17.548 | 19,620 | 394 |
Solstrålning kan jämföras med svartkroppsstrålning vid ca 5778 K (men se graf). Tabellen till höger visar hur strålningen från en svart kropp vid denna temperatur delas upp, och även hur solljus delas upp för jämförelse. Som jämförelse visas också en planet modellerad som en svart kropp, som strålar ut med nominella 288 K (15 °C) som ett representativt värde för jordens mycket varierande temperatur. Dess våglängder är mer än tjugo gånger solens, tabellerade i den tredje kolumnen i mikrometer (tusentals nanometer).
Det vill säga, endast 1 % av solens strålning är vid våglängder kortare än 296 nm, och endast 1 % vid längre än 3728 nm. Uttryckt i mikrometer placerar detta 98 % av solens strålning i området från 0,296 till 3,728 µm. Motsvarande 98 % av energin som utstrålas från en 288 K planet är från 5,03 till 79,5 µm, långt över området för solstrålning (eller under om uttryckt i termer av frekvenser ν = c / λ istället för våglängder λ ) .
En konsekvens av denna mer än en storleksordningsskillnad i våglängd mellan sol- och planetstrålning är att filter konstruerade för att passera det ena och blockera det andra är lätta att konstruera. Till exempel passerar fönster tillverkade av vanligt glas eller genomskinlig plast minst 80 % av den inkommande 5778 K solstrålningen, som är under 1,2 µm i våglängd, samtidigt som de blockerar över 99 % av den utgående 288 K värmestrålningen från 5 µm och uppåt, våglängder där de flesta typer av glas och plast av konstruktionsgradig tjocklek är effektivt ogenomskinliga.
Solens strålning är den som anländer till toppen av atmosfären (TOA). Som kan utläsas från tabellen är strålning under 400 nm, eller ultraviolett , cirka 8 %, medan den över 700 nm, eller infraröd , börjar vid ungefär 48 %-punkten och står därför för 52 % av totalen. Därför är endast 40% av TOA-instrålningen synlig för det mänskliga ögat. Atmosfären förskjuter dessa procentsatser väsentligt till förmån för synligt ljus eftersom den absorberar det mesta av ultraviolett ljus och betydande mängder infrarött.
Härledning
Betrakta en kub av sida L med ledande väggar fyllda med elektromagnetisk strålning i termisk jämvikt vid temperatur T . Om det finns ett litet hål i en av väggarna kommer strålningen som sänds ut från hålet att vara karakteristisk för en perfekt svart kropp . Vi kommer först att beräkna den spektrala energitätheten i kaviteten och sedan bestämma den spektrala strålningen för den emitterade strålningen.
Vid kubens väggar måste den parallella komponenten av det elektriska fältet och den ortogonala komponenten av magnetfältet försvinna. Analogt med vågfunktionen för en partikel i en låda finner man att fälten är överlagringar av periodiska funktioner. De tre våglängderna λ 1 , λ 2 och λ 3 , i de tre riktningarna ortogonala mot väggarna kan vara:
-
()
Talet r kan tolkas som antalet fotoner i moden. För r = 0 är energin i moden inte noll. Denna vakuumenergi i det elektromagnetiska fältet är ansvarig för Casimir-effekten . I det följande kommer vi att beräkna lådans inre energi vid absolut temperatur T .
Enligt statistisk mekanik ges jämviktssannolikhetsfördelningen över energinivåerna för ett visst läge av:
Här
Nämnaren Z ( β ) , är partitionsfunktionen för ett enkelläge och gör P r korrekt normaliserad:
Här har vi implicit definierat
Denna formel, förutom den första vakuumenergitermen, är ett specialfall av den allmänna formeln för partiklar som följer Bose–Einsteins statistik . Eftersom det inte finns någon begränsning på det totala antalet fotoner är den kemiska potentialen noll.
Om vi mäter energin i förhållande till grundtillståndet, följer den totala energin i rutan genom att summera ⟨ E ⟩ − ε / 2 över alla tillåtna enstaka fotontillstånd. Detta kan göras exakt inom den termodynamiska gränsen när L närmar sig oändligheten. I denna gräns ε kontinuerlig och vi kan sedan integrera ⟨ E ⟩ − ε / 2 över denna parameter. För att beräkna energin i lådan på detta sätt måste vi utvärdera hur många fotontillstånd det finns i ett givet energiområde. Om vi skriver det totala antalet enskilda fotontillstånd med energier mellan ε och ε + dε som g ( ε ) dε , där g ( ε ) är densiteten av tillstånd (som utvärderas nedan), så kan vi skriva:
-
()
För att beräkna tillståndstätheten skriver vi om ekvation ( 1 ) enligt följande:
För varje vektor n med heltalskomponenter större än eller lika med noll finns det två fotontillstånd. Detta betyder att antalet fotontillstånd i en viss region av n -rymden är dubbelt så stor som volymen av den regionen. Ett energiområde på dε motsvarar skalet med tjockleken dn = 2 L / hc d ε i n -utrymme. Eftersom komponenterna i n måste vara positiva, spänner detta skal över en oktant av en sfär. Antalet fotontillstånd g ( ε ) dε , i ett energiområde dε , ges alltså av:
Infogar detta i ekv. ( 2 ) ger:
-
()
Från denna ekvation kan man härleda den spektrala energitätheten som en funktion av frekvensen u ν ( T ) och som en funktion av våglängden u λ ( T ) :
Och:
Detta är också en spektral energitäthetsfunktion med energienheter per våglängdsenhet per volymenhet. Integraler av denna typ för Bose - och Fermi - gaser kan uttryckas i termer av polylogaritmer . I detta fall är det dock möjligt att beräkna integralen i sluten form med endast elementära funktioner. Ersätter
Den totala elektromagnetiska energin inuti lådan ges alltså av:
Kombinationen hc / k B har värdet 14 387 , 770 μm·K .
Detta är inte Stefan –Boltzmann-lagen (som ger den totala energin som utstrålas av en svart kropp per ytenhet per tidsenhet), men den kan skrivas mer kompakt med Stefan–Boltzmann-konstanten σ , vilket ger
Konstanten 4 σ / c kallas ibland för strålningskonstanten.
Eftersom strålningen är densamma i alla riktningar och utbreder sig med ljusets hastighet ( c ), är den spektrala strålningen för strålning som lämnar det lilla hålet
Det kan omvandlas till ett uttryck för B λ ( T ) i våglängdsenheter genom att ersätta ν med c / λ och utvärdera
Dimensionsanalys visar att enheten av steradianer, som visas i nämnaren på höger sida av ekvationen ovan, genereras i och bärs genom härledningen men inte förekommer i någon av dimensionerna för något element på vänster sida av ekvationen.
Denna härledning är baserad på Brehm & Mullin 1989 .
Historia
Balfour Stewart
År 1858 beskrev Balfour Stewart sina experiment med termisk strålningsemission och absorptionsförmåga hos polerade plattor av olika ämnen, jämfört med krafterna hos lampsvarta ytor, vid samma temperatur. Stewart valde lampsvarta ytor som sin referens på grund av olika tidigare experimentella fynd, särskilt de av Pierre Prevost och John Leslie . Han skrev "Lampsvart, som absorberar alla strålar som faller på den, och därför besitter största möjliga absorberande kraft, kommer också att ha den största möjliga strålningskraften."
Stewart mätte utstrålad effekt med en termostapel och känslig galvanometer avläst med mikroskop. Han var sysselsatt med selektiv värmestrålning, som han undersökte med plattor av ämnen som strålade och absorberade selektivt för olika strålningskvaliteter snarare än maximalt för alla strålningskvaliteter. Han diskuterade experimenten i termer av strålar som kunde reflekteras och brytas, och som lydde Helmholtz ömsesidighetsprincipen (även om han inte använde en eponym för det). Han nämnde inte i detta dokument att strålarnas kvaliteter kan beskrivas av deras våglängder, och han använde inte heller spektralupplösningsapparater som prismor eller diffraktionsgitter. Hans arbete var kvantitativt inom dessa begränsningar. Han gjorde sina mätningar i rumstemperatur och snabbt för att fånga sina kroppar i ett tillstånd nära den termiska jämvikt i vilken de hade förberetts genom att värmas till jämvikt med kokande vatten. Hans mätningar bekräftade att ämnen som avger och absorberar selektivt respekterar principen om selektiv jämlikhet av utsläpp och absorption vid termisk jämvikt.
Stewart erbjöd ett teoretiskt bevis för att detta borde vara fallet separat för varje utvald kvalitet av termisk strålning, men hans matematik var inte strikt giltig. Enligt historikern DM Siegel: "Han var inte en utövare av de mer sofistikerade teknikerna inom 1800-talets matematiska fysik; han använde sig inte ens av den funktionella notationen för att hantera spektralfördelningar." Han nämnde inget om termodynamik i detta dokument, även om han hänvisade till bevarande av vis viva . Han föreslog att hans mätningar antydde att strålning både absorberades och sänds ut av partiklar av materia över hela djupet av mediet där den fortplantade sig. Han tillämpade Helmholtz ömsesidighetsprincipen för att redogöra för processerna för materialgränssnittet till skillnad från processerna i det inre materialet. Han drog slutsatsen att hans experiment visade att, i det inre av en inneslutning i termisk jämvikt, strålningsvärmen, reflekterad och emitterad kombinerad, vilket lämnar någon del av ytan, oavsett dess substans, var densamma som skulle ha lämnat samma del av ytan. ytan om den hade bestått av lampsvart. Han nämnde inte möjligheten till perfekt reflekterande väggar; i synnerhet noterade han att högpolerade verkliga fysiska metaller absorberar mycket lite.
Gustav Kirchhoff
År 1859, utan att känna till Stewarts arbete, rapporterade Gustav Robert Kirchhoff sammanträffandet av våglängderna för spektralt upplösta absorptionslinjer och emission av synligt ljus. Viktigt för termisk fysik, observerade han också att ljusa linjer eller mörka linjer var uppenbara beroende på temperaturskillnaden mellan emitter och absorbator.
Kirchhoff fortsatte sedan med att betrakta kroppar som avger och absorberar värmestrålning, i en ogenomskinlig inneslutning eller hålighet, i jämvikt vid temperatur T .
Här används en annan notation än Kirchhoffs. Här betecknar emitteringseffekten E ( T , i ) en dimensionerad mängd, den totala strålningen som emitteras av en kropp märkt med index i vid temperatur T. Det totala absorptionsförhållandet a ( T , i ) för den kroppen är dimensionslöst, förhållandet mellan absorberad och infallande strålning i kaviteten vid temperatur T . (Till skillnad från Balfour Stewarts, hänvisade Kirchhoffs definition av hans absorptionsförhållande inte särskilt till en lampsvart yta som källan till den infallande strålningen.) Således förhållandet E ( T , i ) / a ( T , i ) av emitterande effekt till absorptionsförhållande är en dimensionerad storhet, med dimensionerna av emitterande effekt, eftersom a ( T , i ) är dimensionslös. Även här med a ( λ , T , i ) betecknas kroppens våglängdsspecifika emitterande kraft vid temperatur T ( λ , T , i ) E och det våglängdsspecifika absorptionsförhållandet med . Återigen är förhållandet E ( λ , T , i ) / a ( λ , T , i ) mellan emitterande effekt och absorptionsförhållande en dimensionerad storhet, med dimensionerna för emitterande effekt.
I en andra rapport som gjordes 1859 tillkännagav Kirchhoff en ny allmän princip eller lag som han erbjöd ett teoretiskt och matematiskt bevis för, även om han inte erbjöd kvantitativa mätningar av strålningseffekter. Hans teoretiska bevis var och anses fortfarande av vissa författare vara ogiltigt. Hans princip har dock bestått: det var att för värmestrålar med samma våglängd, i jämvikt vid en given temperatur, har det våglängdsspecifika förhållandet mellan emitterande effekt och absorptionsförhållande ett och samma gemensamt värde för alla kroppar som avger och absorbera vid den våglängden. I symboler slog lagen fast att det våglängdsspecifika förhållandet E ( λ , T , i ) / a ( λ , T , i ) har ett och samma värde för alla kroppar, det vill säga för alla värden på index i . I denna rapport nämndes inget om svarta kroppar.
År 1860, fortfarande utan att känna till Stewarts mätningar för utvalda strålningskvaliteter, påpekade Kirchhoff att det länge var etablerat experimentellt att för total värmestrålning, av ovald kvalitet, utsänd och absorberad av en kropp i jämvikt, det dimensionerade totala strålningsförhållandet E ( T , i ) / a ( T , i ) , har ett och samma värde gemensamt för alla kroppar, det vill säga för varje värde av materialindexet i . Återigen utan mätningar av strålningseffekter eller andra nya experimentella data, erbjöd Kirchhoff sedan ett nytt teoretiskt bevis på sin nya princip om universaliteten av värdet av det våglängdsspecifika förhållandet E ( λ , T , i ) / a ( λ , T , i ) vid termisk jämvikt. Hans färska teoretiska bevis var och anses fortfarande av vissa författare vara ogiltigt.
Men ännu viktigare, det förlitade sig på ett nytt teoretiskt postulat om "perfekt svarta kroppar", vilket är anledningen till att man talar om Kirchhoffs lag. Sådana svarta kroppar visade fullständig absorption i sin oändligt tunna ytligaste yta. De motsvarar Balfour Stewarts referenskroppar, med inre strålning, belagda med lampsvart. De var inte de mer realistiska perfekt svarta kropparna som senare övervägdes av Planck. Plancks svarta kroppar utstrålade och absorberades endast av materialet i deras inre; deras gränssnitt med sammanhängande media var endast matematiska ytor, varken kapabla till absorption eller emission, utan endast att reflektera och sända med brytning.
Kirchhoffs bevis betraktade som en godtycklig icke-ideal kropp märkt i såväl som olika perfekta svarta kroppar märkta BB . Det krävde att kropparna hölls i en hålighet i termisk jämvikt vid temperatur T . Hans bevis syftade till att visa att förhållandet E ( λ , T , i ) / a ( λ , T , i ) var oberoende av naturen i hos den icke-idealiska kroppen, hur delvis transparent eller delvis reflekterande den var.
Hans bevis hävdade först att för våglängden λ och vid temperatur T , vid termisk jämvikt, har alla perfekt svarta kroppar av samma storlek och form samma gemensamma värde för emissionskraft E ( λ , T , BB) , med dimensionerna av makt. Hans bevis noterade att det dimensionslösa våglängdsspecifika absorptionsförhållandet a ( λ , T , BB) för en perfekt svart kropp per definition är exakt 1. Sedan för en perfekt svart kropp, det våglängdsspecifika förhållandet mellan emissionseffekt och absorptionsförhållande E ( λ , T , BB) / a ( λ , T , BB) är återigen bara E ( λ , T , BB) , med kraftens dimensioner. Kirchhoff ansåg, successivt, termisk jämvikt med den godtyckliga icke-idealkroppen, och med en perfekt svart kropp av samma storlek och form, på plats i sin hålighet i jämvikt vid temperatur T . Han menade att flödena av värmestrålning måste vara desamma i varje fall. Således hävdade han att vid termisk jämvikt var förhållandet E ( λ , T , i ) / a ( λ , T , i ) lika med E ( λ , T , BB) , vilket nu kan betecknas B λ ( λ , T ) , en kontinuerlig funktion, endast beroende av λ vid fast temperatur T , och en ökande funktion av T vid fast våglängd λ , vid låga temperaturer som försvinner för synliga men inte för längre våglängder, med positiva värden för synliga våglängder vid högre temperaturer, vilket inte beror på arten i hos den godtyckliga icke-idealkroppen. (Geometriska faktorer, som tagits i detalj av Kirchhoff, har ignorerats i det föregående.)
Således kan Kirchhoffs lag om termisk strålning anges: För vilket material som helst, som utstrålar och absorberar i termodynamisk jämvikt vid varje given temperatur T , för varje våglängd λ , har förhållandet mellan emissiv effekt och absorptionsförhållande ett universellt värde, vilket är karakteristiskt för en perfekt svart kropp, och är en emissionskraft som vi här representerar av B λ ( λ , T ) . (För vår notation B λ ( λ , T ) var Kirchhoffs ursprungliga notation helt enkelt e .)
Kirchhoff meddelade att bestämningen av funktionen B λ ( λ , T ) var ett problem av största vikt, även om han insåg att det skulle finnas experimentella svårigheter att övervinna. Han antog att det, liksom andra funktioner som inte beror på egenskaperna hos enskilda kroppar, skulle vara en enkel funktion. Den funktionen B λ ( λ , T ) har ibland kallats 'Kirchhoffs (emission, universella) funktion', även om dess exakta matematiska form inte skulle vara känd förrän i fyrtio år tills den upptäcktes av Planck 1900. Det teoretiska beviset för Kirchhoffs universalitetsprincip arbetades på och debatterades av olika fysiker under samma tid och senare. Kirchhoff konstaterade senare 1860 att hans teoretiska bevis var bättre än Balfour Stewarts, och i vissa avseenden var det så. Kirchhoffs papper från 1860 nämnde inte termodynamikens andra lag och nämnde naturligtvis inte begreppet entropi som inte hade etablerats vid den tiden. I en mer övervägd redogörelse i en bok 1862 nämnde Kirchhoff sambandet mellan sin lag och "Carnots princip", som är en form av den andra lagen.
Enligt Helge Kragh har "kvantteorin sitt ursprung till studiet av termisk strålning, i synnerhet till den "svarta kropps"-strålningen som Robert Kirchhoff först hade definierat 1859–1860."
Empiriska och teoretiska ingredienser för den vetenskapliga induktionen av Plancks lag
År 1860 förutspådde Kirchhoff experimentella svårigheter för den empiriska bestämningen av funktionen som beskrev beroendet av svartkroppsspektrat som en funktion endast av temperatur och våglängd. Och så blev det. Det tog cirka fyrtio år av utveckling av förbättrade metoder för mätning av elektromagnetisk strålning för att få ett tillförlitligt resultat.
År 1865 beskrev John Tyndall strålning från elektriskt uppvärmda filament och från kolbågar som synlig och osynlig. Tyndall sönderdelade strålningen spektralt med hjälp av ett bergsaltprisma, som passerade såväl värme som synliga strålar, och mätte strålningsintensiteten med hjälp av en termostapel.
År 1880 publicerade André-Prosper-Paul Crova ett diagram över det tredimensionella utseendet på grafen över styrkan hos termisk strålning som en funktion av våglängd och temperatur. Han bestämde den spektrala variabeln med hjälp av prismor. Han analyserade ytan genom vad han kallade "isotermiska" kurvor, sektioner för en enda temperatur, med en spektral variabel på abskissan och en effektvariabel på ordinatan. Han satte jämna kurvor genom sina experimentella datapunkter. De hade en topp vid ett spektralvärde som är karakteristiskt för temperaturen, och föll på vardera sidan av den mot den horisontella axeln. Sådana spektralsektioner visas i stor utsträckning även idag.
I en serie tidningar från 1881 till 1886 rapporterade Langley mätningar av värmestrålningens spektrum, med hjälp av diffraktionsgitter och prismor, och de mest känsliga detektorer han kunde göra. Han rapporterade att det fanns en toppintensitet som ökade med temperaturen, att formen på spektrumet inte var symmetrisk om toppen, att det fanns ett kraftigt fall av intensitet när våglängden var kortare än ett ungefärligt gränsvärde för varje temperatur, att den ungefärliga cut-off-våglängden minskade med ökande temperatur, och att våglängden på toppintensiteten minskade med temperaturen, så att intensiteten ökade kraftigt med temperaturen för korta våglängder som var längre än den ungefärliga cut-off för temperaturen.
Efter att ha läst Langley publicerade den ryske fysikern VA Michelson 1888 en övervägande av idén att den okända Kirchhoff-strålningsfunktionen kunde förklaras fysiskt och anges matematiskt i termer av "fullständig oregelbundenhet i vibrationerna hos ... atomer". Vid den här tiden studerade Planck inte strålning noggrant och trodde varken på atomer eller statistisk fysik. Michelson tog fram en formel för spektrumet för temperatur:
1898 publicerade Otto Lummer och Ferdinand Kurlbaum en redogörelse för sin hålighetsstrålningskälla. Deras design har använts i stort sett oförändrad för strålningsmätningar fram till idag. Det var en platinalåda, delad av membran, med dess insida svärtad med järnoxid. Det var en viktig ingrediens för de successivt förbättrade mätningarna som ledde till upptäckten av Plancks lag. En version som beskrevs 1901 hade sin interiör svärtad med en blandning av krom-, nickel- och koboltoxider.
Vikten av strålningskällan Lummer och Kurlbaum var att den var en experimentellt tillgänglig källa för svartkroppsstrålning, till skillnad från strålning från en enkelt exponerad glödande fast kropp, som hade varit den närmaste tillgängliga experimentella approximationen till svartkroppsstrålning över ett lämpligt temperaturintervall. De enkelt exponerade glödande fasta kropparna, som hade använts tidigare, avgav strålning med avvikelser från svartkroppens spektrum som gjorde det omöjligt att hitta det sanna svartkroppsspektrat från experiment.
Plancks åsikter innan de empiriska fakta ledde till att han hittade sin eventuella lag
Planck riktade sin uppmärksamhet först mot problemet med svartkroppsstrålning 1897. Teoretiska och empiriska framsteg gjorde det möjligt för Lummer och Pringsheim att 1899 skriva att tillgängliga experimentella bevis ungefär överensstämde med den specifika intensitetslagen Cλ −5 e − c ⁄ λT där C och c betecknar empiriskt mätbara konstanter, och där X och T betecknar våglängd respektive temperatur. Av teoretiska skäl accepterade Planck vid den tiden denna formulering, som har en effektiv cut-off av korta våglängder.
Gustav Kirchhoff var Max Plancks lärare och anade att det fanns en universell lag för svartkroppsstrålning och detta kallades "Kirchhoffs utmaning". Planck, en teoretiker, trodde att Wilhelm Wien hade upptäckt denna lag och Planck utökade Wiens arbete när han presenterade den 1899 för mötet med German Physical Society. Experimentalisterna Otto Lummer , Ferdinand Kurlbaum , Ernst Pringsheim Sr. och Heinrich Rubens gjorde experiment som verkade stödja Wiens lag, särskilt vid korta våglängder med högre frekvens, vilket Planck så fullständigt stödde vid German Physical Society att det började kallas Wien-Planck-lagen . Men i september 1900 hade experimentalisterna bevisat bortom allt tvivel att Wien-Planck-lagen misslyckades vid de längre våglängderna. De skulle presentera sina uppgifter den 19 oktober. Planck informerades av sin vän Rubens och skapade snabbt en formel inom några dagar. I juni samma år hade Lord Raleigh skapat en formel som skulle fungera för korta lägre frekvensvåglängder baserat på den allmänt accepterade teorin om ekvipartition . Så Planck lade fram en formel som kombinerar både Raleighs lag (eller en liknande ekvipartitionsteori) och Wiens lag som skulle vägas till den ena eller den andra lagen beroende på våglängd för att matcha experimentdata. Men även om denna ekvation fungerade, sa Planck själv att om han inte kunde förklara formeln härledd från en "lycklig intuition" till en av "sanna mening" i fysiken, så hade den inte verklig betydelse. Planck förklarade att därefter följde hans livs hårdaste arbete. Planck trodde inte på atomer, och han trodde inte heller att termodynamikens andra lag borde vara statistisk eftersom sannolikhet inte ger ett absolut svar, och Boltzmanns entropilag vilade på hypotesen om atomer och var statistisk. Men Planck kunde inte hitta ett sätt att förena sin Blackbody-ekvation med kontinuerliga lagar som Maxwells vågekvationer. Så i vad Planck kallade "en handling av desperation" vände han sig till Boltzmanns atomlag för entropi eftersom det var den enda som fick hans ekvation att fungera. Därför använde han Boltzmann-konstanten k och sin nya konstant h för att förklara lagen om svartkroppsstrålning som blev allmänt känd genom hans publicerade tidning.
Att hitta den empiriska lagen
Max Planck producerade sin lag den 19 oktober 1900 som en förbättring av Wien-approximationen , publicerad 1896 av Wilhelm Wien , som passade experimentella data vid korta våglängder (höga frekvenser) men avvek från dem vid långa våglängder (låga frekvenser). I juni 1900, baserat på heuristiska teoretiska överväganden, hade Rayleigh föreslagit en formel som han föreslog skulle kunna kontrolleras experimentellt. Förslaget var att Stewart–Kirchhoffs universella funktion kunde ha formen c 1 Tλ −4 exp(– c 2 / λT ) . Detta var inte den berömda Rayleigh–Jeans-formeln 8π k B Tλ −4 , som inte dök upp förrän 1905, även om den reducerades till den senare för långa våglängder, vilket är de relevanta här. Enligt Klein kan man spekulera i att det är troligt att Planck hade sett detta förslag även om han inte nämnde det i sina tidningar från 1900 och 1901. Planck skulle ha varit medveten om olika andra föreslagna formler som hade erbjudits. Den 7 oktober 1900 berättade Rubens för Planck att i den komplementära domänen (lång våglängd, låg frekvens), och bara där, passade Rayleighs 1900-formel väl in på de observerade data.
För långa våglängder innebar Rayleighs heuristiska formel från 1900 ungefär att energin var proportionell mot temperaturen, U λ = const. T . Det är känt att dS / dU λ = 1 / T och detta leder till att dS / dU λ = konst. / U λ och därifrån till d 2 S / dU λ 2 = − konst. / U λ 2 för långa våglängder. Men för korta våglängder leder Wien-formeln till 1 / T = − const. l U λ + konst. och därifrån till d 2 S / dU λ 2 = − konst. / U λ för korta våglängder. Planck kanske lappade ihop dessa två heuristiska formler, för långa och för korta våglängder, för att skapa en formel
Detta ledde Planck till formeln
Planck skickade detta resultat till Rubens, som jämförde det med hans och Kurlbaums observationsdata och fann att det passade för alla våglängder anmärkningsvärt bra. Den 19 oktober 1900 rapporterade Rubens och Kurlbaum kort passformen till uppgifterna, och Planck lade till en kort presentation för att ge en teoretisk skiss för att redogöra för sin formel. Inom en vecka gav Rubens och Kurlbaum en mer fullständig rapport om sina mätningar som bekräftade Plancks lag. Deras teknik för spektral upplösning av den längre våglängdsstrålningen kallades för reststrålemetoden. Strålarna reflekterades upprepade gånger från polerade kristallytor, och strålarna som tog sig hela vägen genom processen var "rester" och hade våglängder som företrädesvis reflekterades av kristaller av lämpligt specifika material.
Försöker hitta en fysisk förklaring av lagen
När Planck väl hade upptäckt den empiriskt passande funktionen, konstruerade han en fysisk härledning av denna lag. Hans tänkande kretsade kring entropi snarare än att vara direkt om temperatur. Planck betraktade ett hålrum med perfekt reflekterande väggar; inuti kaviteten finns det ändligt många distinkta men identiskt konstituerade resonansoscillerande kroppar av bestämd storlek, med flera sådana oscillatorer vid var och en av ändligt många karakteristiska frekvenser. Dessa hypotetiska oscillatorer var för Planck rent imaginära teoretiska undersökningssonder, och han sa om dem att sådana oscillatorer inte behöver "verkligen existera någonstans i naturen, förutsatt att deras existens och deras egenskaper överensstämmer med termodynamikens och elektrodynamikens lagar." Planck tillskrev inte sin hypotes om resonansoscillatorer någon bestämd fysisk betydelse utan föreslog den snarare som en matematisk anordning som gjorde det möjligt för honom att härleda ett enda uttryck för det svarta kroppens spektrum som matchade empiriska data på alla våglängder. Han nämnde preliminärt det möjliga sambandet mellan sådana oscillatorer och atomer . På sätt och vis motsvarade oscillatorerna Plancks kolfläck; storleken på fläcken kan vara liten oavsett storleken på kaviteten, förutsatt att fläcken effektivt transducerade energi mellan strålningsvåglängdsmoder.
Delvis efter en heuristisk beräkningsmetod som Boltzmann banat väg för gasmolekyler, övervägde Planck de möjliga sätten att fördela elektromagnetisk energi över de olika lägena hos hans hypotetiska laddade materialoscillatorer. Denna acceptans av det probabilistiska tillvägagångssättet, efter Boltzmann, för Planck var en radikal förändring från hans tidigare ståndpunkt, som dittills medvetet hade motsatt sig sådant tänkande som Boltzmann föreslagit. Med Plancks ord: "Jag ansåg att [kvanthypotesen] var ett rent formellt antagande, och jag tänkte inte så mycket på det förutom detta: att jag hade fått ett positivt resultat under alla omständigheter och till vilket pris som helst." Heuristiskt sett hade Boltzmann fördelat energin i godtyckliga enbart matematiska kvanta ϵ , som han hade fortsatt att göra tenderar till noll i storlek, eftersom den ändliga magnituden ϵ endast hade tjänat till att tillåta definitiv räkning för matematiska beräkningar av sannolikheter, och hade ingen fysisk betydelse. Med hänvisning till en ny universell naturkonstant, h , antog Planck att i de flera oscillatorerna för var och en av de ändligt många karakteristiska frekvenserna, var den totala energin fördelad till var och en i en heltalsmultipel av en bestämd fysisk energienhet, ϵ , inte godtycklig som i Boltzmanns metod, men nu för Planck, i en ny utgång, karakteristisk för respektive karakteristiska frekvens. Hans nya universella naturkonstant, h , är nu känd som Planck-konstanten .
Planck förklarade vidare att den respektive bestämda enheten, ϵ , av energi borde vara proportionell mot den respektive karakteristiska oscillationsfrekvensen ν för den hypotetiska oscillatorn, och 1901 uttryckte han detta med proportionalitetskonstanten h :
Planck föreslog inte att ljus som sprider sig i fritt utrymme kvantiseras. Idén om kvantisering av det fria elektromagnetiska fältet utvecklades senare och införlivades så småningom i vad vi nu känner som kvantfältteori .
1906 erkände Planck att hans imaginära resonatorer, med linjär dynamik, inte gav en fysisk förklaring till energitransduktion mellan frekvenser. Dagens fysik förklarar transduktionen mellan frekvenser i närvaro av atomer genom deras kvantexitabilitet, efter Einstein. Planck trodde att i ett hålrum med perfekt reflekterande väggar och utan någon materia närvarande, kan det elektromagnetiska fältet inte utbyta energi mellan frekvenskomponenter. Detta beror på linjäriteten i Maxwells ekvationer . Dagens kvantfältteori förutspår att, i frånvaro av materia, det elektromagnetiska fältet lyder olinjära ekvationer och i den meningen interagerar själv. Sådan interaktion i frånvaro av materia har ännu inte mätts direkt eftersom det skulle kräva mycket höga intensiteter och mycket känsliga och lågbrusande detektorer, som fortfarande håller på att konstrueras. Planck trodde att ett fält utan växelverkan varken lyder eller bryter mot den klassiska principen om likfördelning av energi, och istället förblir exakt som det var när det introducerades, snarare än att utvecklas till ett svart kroppsfält. Linjäriteten i hans mekaniska antaganden hindrade således Planck från att ha en mekanisk förklaring av maximeringen av entropin i det termodynamiska värmestrålningsfältet i jämvikt. Det är därför han var tvungen att ta till Boltzmanns probabilistiska argument. Några nya förslag i den möjliga fysikaliska förklaringen av Planck-konstanten tyder på att, i enlighet med de Broglies anda av våg-partikeldualitet , om, när man betraktar strålningen som ett vågpaket, Planck-konstanten bestäms av de fysikaliska egenskaperna hos vakuumet och en kritisk mängd störningar i det elektromagnetiska fältet.
Plancks lag kan anses uppfylla Gustav Kirchhoffs förutsägelse att hans lag om värmestrålning var av högsta betydelse. I sin mogna presentation av sin egen lag erbjöd Planck ett grundligt och detaljerat teoretiskt bevis för Kirchhoffs lag, vilket fram till dess ibland hade diskuterats teoretiska bevis för, delvis för att det sades förlita sig på opysiska teoretiska objekt, såsom Kirchhoffs perfekt absorberande oändligt. tunn svart yta.
Efterföljande händelser
Det var inte förrän fem år efter att Planck gjorde sitt heuristiska antagande om abstrakta element av energi eller handling som Albert Einstein tänkte på verkligt existerande ljuskvanta 1905 som en revolutionerande förklaring av svartkroppsstrålning, av fotoluminescens, av den fotoelektriska effekten , och jonisering av gaser med ultraviolett ljus. År 1905 "trodde Einstein att Plancks teori inte kunde fås att överensstämma med idén om ljuskvanta, ett misstag som han rättade till 1906." I motsats till Plancks tro på den tiden, föreslog Einstein en modell och formel där ljus sänds ut, absorberades och fortplantades i fritt utrymme i energikvanta lokaliserade i punkter i rymden. Som en introduktion till sitt resonemang rekapitulerade Einstein Plancks modell av hypotetiska elektriska oscillatorer i resonansmaterial som strålningskällor och sänkor, men sedan kom han med ett nytt argument, bortkopplat från den modellen, men delvis baserat på ett termodynamiskt argument från Wien, där Plancks formeln ϵ = hν spelade ingen roll. Einstein gav energiinnehållet i sådana kvanta i formen Rβν / N . Således motsatte Einstein Plancks vågformiga teori om ljus. 1910, när han kritiserade ett manuskript som Planck skickade till honom, i vetskap om att Planck var en stadig anhängare av Einsteins speciella relativitetsteori, skrev Einstein till Planck: "För mig verkar det absurt att ha energi kontinuerligt distribuerad i rymden utan att anta en eter."
Enligt Thomas Kuhn var det inte förrän 1908 som Planck mer eller mindre accepterade en del av Einsteins argument för fysisk till skillnad från abstrakt matematisk diskretitet i termisk strålningsfysik. Fortfarande 1908, med tanke på Einsteins förslag om kvantal spridning, ansåg Planck att ett sådant revolutionärt steg kanske var onödigt. Fram till dess hade Planck varit konsekvent i att tro att diskreta verkningskvanta varken fanns i hans resonansoscillatorer eller i utbredningen av termisk strålning. Kuhn skrev att det i Plancks tidigare artiklar och i hans monografi från 1906 inte finns något "omnämnande av diskontinuitet, [inte heller] om tal om en begränsning av oscillatorenergi, [eller om] någon formel som U = nhν . " Kuhn påpekade att hans studie av Plancks uppsatser från 1900 och 1901, och av hans monografi från 1906, hade lett honom till "kättarska" slutsatser, i motsats till de utbredda antagandena från andra som bara såg Plancks författarskap utifrån ett senare, anakronistiskt perspektiv. synpunkter. Kuhns slutsatser, som fann en period fram till 1908, då Planck konsekvent höll sin "första teori", har accepterats av andra historiker.
I den andra upplagan av sin monografi, 1912, vidhöll Planck sin avståndstagande från Einsteins förslag om ljuskvanta. Han föreslog i viss detalj att absorptionen av ljus av hans virtuella materialresonatorer kan vara kontinuerlig, ske med en konstant hastighet i jämvikt, till skillnad från kvantal absorption. Endast utsläppen var kvantala. Detta har ibland kallats Plancks "andra teori".
Det var inte förrän 1919 som Planck i den tredje upplagan av sin monografi mer eller mindre accepterade sin "tredje teori", att både emission och absorption av ljus var kvantala.
Den färgglada termen " ultraviolett katastrof " gavs av Paul Ehrenfest 1911 till det paradoxala resultatet att den totala energin i kaviteten tenderar till oändlighet när ekvipartitionssatsen för klassisk statistisk mekanik (av misstag) tillämpas på strålning från svarta kroppar. Men detta hade inte varit en del av Plancks tänkande, eftersom han inte hade försökt tillämpa doktrinen om ekvipartition: när han gjorde sin upptäckt 1900 hade han inte märkt någon form av "katastrof". Det noterades först av Lord Rayleigh 1900 och sedan 1901 av Sir James Jeans ; och senare, 1905, av Einstein när han ville stödja idén att ljus fortplantas som diskreta paket, senare kallade "fotoner", och av Rayleigh och av Jeans.
År 1913 gav Bohr en annan formel med ytterligare en annan fysisk betydelse till kvantiteten hν . I motsats till Plancks och Einsteins formler hänvisade Bohrs formel uttryckligen och kategoriskt till atomernas energinivåer. Bohrs formel var W τ 2 − W τ 1 = hν där W τ 2 och W τ 1 betecknar energinivåerna för en atoms kvanttillstånd, med kvanttalen τ 2 och τ 1 . Symbolen ν anger frekvensen av ett kvantum av strålning som kan sändas ut eller absorberas när atomen passerar mellan dessa två kvanttillstånd. I motsats till Plancks modell har frekvensen ingen omedelbar relation till frekvenser som kan beskriva dessa kvanttillstånd i sig.
Senare, 1924, utvecklade Satyendra Nath Bose teorin om fotonernas statistiska mekanik, vilket möjliggjorde en teoretisk härledning av Plancks lag. Det faktiska ordet "foton" uppfanns ännu senare, av GN Lewis 1926, som av misstag trodde att fotoner var bevarade, i motsats till Bose–Einsteins statistik; icke desto mindre antogs ordet "foton" för att uttrycka Einsteins postulat om ljusutbredningens paketnatur. I ett elektromagnetiskt fält isolerat i ett vakuum i ett kärl med perfekt reflekterande väggar, såsom Planck ansåg, skulle fotonerna verkligen bevaras enligt Einsteins 1905-modell, men Lewis syftade på ett fält av fotoner som betraktades som ett system stängt med respekt för övervägbar materia men öppen för utbyte av elektromagnetisk energi med ett omgivande system av övervägbar materia, och han föreställde sig felaktigt att fotonerna fortfarande var bevarade, lagrade inuti atomer.
I slutändan bidrog Plancks lag om svartkroppsstrålning till Einsteins koncept av ljuskvanta som bär linjärt momentum, vilket blev den grundläggande grunden för utvecklingen av kvantmekaniken .
Den ovan nämnda linjäriteten i Plancks mekaniska antaganden, som inte tillåter energetisk interaktion mellan frekvenskomponenter, ersattes 1925 av Heisenbergs ursprungliga kvantmekanik. I sin artikel som lämnades in den 29 juli 1925 redogjorde Heisenbergs teori för Bohrs ovan nämnda formel från 1913. Den medgav icke-linjära oscillatorer som modeller av atomära kvanttillstånd, vilket möjliggjorde energetisk interaktion mellan deras egna multipla interna diskreta Fourierfrekvenskomponenter, vid tillfällen av emission eller absorption av mängder av strålning. Frekvensen av ett strålningskvant var den för en bestämd koppling mellan inre atomära metastabila oscillerande kvanttillstånd. Vid den tiden visste Heisenberg ingenting om matrisalgebra, men Max Born läste manuskriptet till Heisenbergs tidning och kände igen matriskaraktären i Heisenbergs teori. Sedan publicerade Born och Jordan en explicit matristeori om kvantmekanik, baserad på, men i form tydligt skild från, Heisenbergs ursprungliga kvantmekanik; det är Born and Jordan-matristeorin som idag kallas matrismekanik. Heisenbergs förklaring av Planck-oscillatorerna, som icke-linjära effekter som är uppenbara som Fourier-lägen för transienta processer av emission eller absorption av strålning, visade varför Plancks oscillatorer, betraktade som bestående fysiska objekt som kan föreställas av klassisk fysik, inte gav en adekvat förklaring av fenomenen.
Nuförtiden, som ett uttryck för energin i ett ljuskvantum, finner man ofta formeln E = ħω , där ħ = h / 2π , och ω = 2π ν betecknar vinkelfrekvens, och mer sällan den ekvivalenta formeln E = hν . Detta uttalande om ett verkligt existerande och fortplantande ljuskvantum, baserat på Einsteins, har en annan fysisk betydelse än Plancks ovanstående uttalande ϵ = hν om de abstrakta energienheterna som ska fördelas bland hans hypotetiska resonansmaterialoscillatorer.
En artikel av Helge Kragh publicerad i Physics World ger en redogörelse för denna historia.
Se även
Bibliografi
- Adkins, CJ (1983). Equilibrium Thermodynamics (3:e upplagan). Cambridge University Press . ISBN 978-0-521-25445-8 .
- Andrews, David (2000). En introduktion till atmosfärsfysik . Cambridge University Press. ISBN 0511800770 .
- Bohr, N. (1913). "Om konstitutionen av atomer och molekyler" (PDF) . Filosofisk tidskrift . 26 (153): 1–25. Bibcode : 1913PMag...26..476B . doi : 10.1080/14786441308634993 .
- Bohren, CF ; Clothiaux, EE (2006). Grunderna för atmosfärisk strålning . Wiley-VCH . ISBN 978-3-527-40503-9 .
- Boltzmann, L. (1878). "Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung, respective den Sätzen über das Wärmegleichgewicht". Sitzungsberichte Mathematisch-Naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften i Wien . 76 (2): 373–435.
- Born, M. ; Wolf, E. (1999). Principles of Optics (7:e upplagan). Cambridge University Press . ISBN 978-0-521-64222-4 .
- Born, M. ; Jordan, P. (1925). "Zur Quantenmechanik". Zeitschrift für Physik . 34 (1): 858–888. Bibcode : 1925ZPhy...34..858B . doi : 10.1007/BF01328531 . S2CID 186114542 . Översatt delvis som "Om kvantmekanik" i van der Waerden, BL (1967). Källor till kvantmekanik . North-Holland Publishing . s. 277–306.
- Bose, Satyendra Nath (1924). "Plancks Gesetz und Lichtquantenhypothese". Zeitschrift für Physik (på tyska). 26 (1): 178–181. Bibcode : 1924ZPhy...26..178B . doi : 10.1007/BF01327326 . S2CID 186235974 .
- Brehm, JJ; Mullin, WJ (1989). Introduktion till materiens struktur . Wiley . ISBN 978-0-471-60531-7 .
- Brillouin, L. (1970). Relativitet omprövat . Akademisk press . ISBN 978-0-12-134945-5 .
- Caniou, J. (1999). Passiv infraröd detektion: teori och tillämpningar . Springer . ISBN 978-0-7923-8532-5 .
- Chandrasekhar, S. (1960) [1950]. Radiative Transfer (Reviderad reprint ed.). Dover Publikationer . ISBN 978-0-486-60590-6 .
- Chang, Donald C. (2017). "Fysisk tolkning av Plancks konstant baserat på Maxwell-teorin". Kinesisk fysik B . 26 (4). 040301. arXiv : 1706.04475 . Bibcode : 2017ChPhB..26d0301C . doi : 10.1088/1674-1056/26/4/040301 . S2CID 119415586 .
- Cotton, A. (1899). "Kirchhoffs lags nuvarande status". The Astrophysical Journal . 9 : 237-268. Bibcode : 1899ApJ.....9..237C . doi : 10.1086/140585 .
- Crova, APP (1880). "Étude des radiations émises par les corps incandescents. Mesure optique des hautes températures" . Annales de chimie et de physique . Serie 5. 19 : 472–550.
- Dougal, RC (1976). "Presentationen av Plancks strålningsformel (handledning)". Fysisk utbildning . 11 (6): 438–443. Bibcode : 1976PhyEd..11..438D . doi : 10.1088/0031-9120/11/6/008 . S2CID 250881729 .
- Ehrenfest, P. (1911). "Welche Züge der Lichtquantenhypothese spielen in der Theorie der Wärmestrahlung eine wesentliche Rolle?" . Annalen der Physik . 36 (11): 91–118. Bibcode : 1911AnP...341...91E . doi : 10.1002/andp.19113411106 .
- Ehrenfest, P .; Kamerlingh Onnes, H. (1914). "Förenklat utdrag av formeln från teorin om kombinationer som Planck använder som grund för sin strålningsteori". Proceedings av Royal Dutch Academy of Sciences i Amsterdam . 17 (2): 870–873. Bibcode : 1914KNAB...17..870E .
- Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" . Annalen der Physik . 17 (6): 132–148. Bibcode : 1905AnP...322..132E . doi : 10.1002/andp.19053220607 . Översatt i Arons, AB; Peppard, MB (1965). "Einsteins förslag till fotonkonceptet: En översättning av Annalen der Physik -papperet från 1905" (PDF) . American Journal of Physics . 33 (5): 367. Bibcode : 1965AmJPh..33..367A . doi : 10.1119/1.1971542 . Arkiverad från originalet (PDF) den 4 mars 2016 . Hämtad 19 april 2011 .
- Einstein, A. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft Zürich . 18 :47–62. och en nästan identisk version Einstein, A. (1917). "Zur Quantentheorie der Strahlung". Fysikaliska Zeitschrift . 18 : 121–128. Bibcode : 1917PhyZ...18..121E . Översatt i ter Haar, D. (1967). "Om kvantteorin om strålning" . Den gamla kvantteorin . Pergamon Press . s. 167–183. LCCN 66029628 . Se även [1] .
- Einstein, A. (1993). Albert Einsteins samlade papper . Vol. 3. Engelsk översättning av Beck, A. Princeton University Press . ISBN 978-0-691-10250-4 .
- Feynman, RP ; Leighton, RB ; Sands, M. (1963). Feynman-föreläsningarna om fysik, volym 1 . Addison-Wesley . ISBN 978-0-201-02010-6 .
- Fischer, T. (1 november 2011). "Ämnen: härledning av Plancks lag" . ThermalHUB . Hämtad 19 juni 2015 .
- Gaofeng Shao; Yucao Lu; Dorian AH Hanaor; Sheng Cui; Jian Jiao; Xiaodong Shen (2019). "Förbättrad oxidationsbeständighet av beläggningar med hög emissivitet på fibrös keramik för återanvändbara rymdsystem" . Korrosionsvetenskap . Elsevier. 146 : 233–246. arXiv : 1902.03943 . doi : 10.1016/j.corsci.2018.11.006 . S2CID 118927116 . HAL Id: hal-02308467 – via HAL arkiv ouverts.
- Goody, RM; Yung, YL (1989). Atmospheric Radiation: Theoretical Basis (2nd ed.). Oxford University Press . ISBN 978-0-19-510291-8 .
- Guggenheim, EA (1967). Termodynamik. An Advanced Treatment for Chemists and Physicists (5:e reviderade upplagan). North-Holland Publishing Company .
- Haken, H. (1981). Light (Reprint ed.). Amsterdam: North-Holland Publishing . ISBN 978-0-444-86020-0 .
- Hapke, B. (1993). Teori om reflektans och emittansspektroskopi . Cambridge University Press , Cambridge, Storbritannien. ISBN 978-0-521-30789-5 .
- Heisenberg, W. (1925). "Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen". Zeitschrift für Physik . 33 (1): 879–893. Bibcode : 1925ZPhy...33..879H . doi : 10.1007/BF01328377 . S2CID 186238950 . Översatt som "Quantum-theoretical Re-interpretation of kinematic and mechanical relations" i van der Waerden, BL (1967). Källor till kvantmekanik . North-Holland Publishing . s. 261–276.
- Heisenberg, W. (1930). De fysiska principerna för kvantteorin . Eckart, C.; Hoyt, FC (översättning). University of Chicago Press .
- Hermann, A. (1971). Uppkomsten av kvantteorin . Nash, CW (översättning). MIT Tryck på . ISBN 978-0-262-08047-7 . en översättning av Frühgeschichte der Quantentheorie (1899–1913) , Physik Verlag, Mosbach/Baden, 1969.
- Hettner, G. (1922). "Die Bedeutung von Rubens Arbeiten für die Plancksche Strahlungsformel" . Naturwissenschaften . 10 (48): 1033–1038. Bibcode : 1922NW.....10.1033H . doi : 10.1007/BF01565205 . S2CID 46268714 .
- Jammer, M. (1989). The Conceptual Development of Quantum Mechanics (andra upplagan). Tomash Publishers / American Institute of Physics . ISBN 978-0-88318-617-6 .
- Jauch, JM; Rohrlich, F. (1980) [1955]. Teorin om fotoner och elektroner. Den relativistiska kvantfältsteorin för laddade partiklar med en halv spin ( andra upplagan av andra upplagan). Springer . ISBN 978-0-387-07295-1 .
- Jeans, JH (1901). "Fördelningen av molekylär energi" . Royal Societys filosofiska transaktioner A . 196 (274–286): 397–430. Bibcode : 1901RSPTA.196..397J . doi : 10.1098/rsta.1901.0008 . JSTOR 90811 .
- Jeans, JH (1905a). "XI. Om energifördelningen mellan materia och eter" . Filosofisk tidskrift . 10 (55): 91–98. doi : 10.1080/14786440509463348 .
- Jeans, JH (1905b). "Om tillämpningen av statistisk mekanik på materiens och eters allmänna dynamik" . Kungliga sällskapets handlingar A . 76 (510): 296–311. Bibcode : 1905RSPSA..76..296J . doi : 10.1098/rspa.1905.0029 . JSTOR 92714 .
- Jeans, JH (1905c). "En jämförelse mellan två teorier om strålning" . Naturen . 72 (1865): 293–294. Bibcode : 1905Natur..72..293J . doi : 10.1038/072293d0 . S2CID 3955227 .
- Jeans, JH (1905d). "Om strålningens lagar" . Kungliga sällskapets handlingar A . 76 (513): 545–552. Bibcode : 1905RSPSA..76..545J . doi : 10.1098/rspa.1905.0060 . JSTOR 92704 .
- Jeffreys, H. (1973). Scientific Inference (3:e upplagan). Cambridge University Press . ISBN 978-0-521-08446-8 .
- Kangro, H. (1976). Tidig historia av Plancks strålningslag . Taylor och Francis . ISBN 978-0-85066-063-0 .
- Karplus, R.; Neuman, M. (1951). "Ljusets spridning genom ljus". Fysisk granskning . 83 (4): 776–784. Bibcode : 1951PhRv...83..776K . doi : 10.1103/PhysRev.83.776 .
- Kirchhoff, GR (1860a). "Über die Fraunhofer'schen Linien". Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin : 662–665.
- Kirchhoff, GR (1860b). "Über den Zusammenhang zwischen Emission und Absorption von Licht und Wärme". Monatsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin : 783–787.
- Kirchhoff, GR (1860c). "Über das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme and Licht" . Annalen der Physik und Chemie . 109 (2): 275–301. Bibcode : 1860AnP...185..275K . doi : 10.1002/andp.18601850205 . Översatt av Guthrie, F. som Kirchhoff, GR (1860). "Om förhållandet mellan olika kroppars strålande och absorberande krafter för ljus och värme". Filosofisk tidskrift . Serie 4. 20 : 1–21.
- Kirchhoff, GR (1862), "Über das Verhältniss zwischen dem Emissionsvermögen und dem Absorptionsvermögen der Körper für Wärme und Licht", Gessamelte Abhandlungen , Johann Ambrosius Barth, s. 571–598
- Kittel, C .; Kroemer, H. (1980). Termisk fysik (2:a upplagan). WH Freeman . ISBN 978-0-7167-1088-2 .
- Klein, MJ (1962). "Max Planck och början av kvantteorin". Arkiv för Exakta Vetenskapshistoria . 1 (5): 459–479. doi : 10.1007/BF00327765 . S2CID 121189755 .
- Kragh, H. (1999). Kvantgenerationer. En historia av fysik under det tjugonde århundradet . Princeton University Press . ISBN 978-0-691-01206-3 .
- Kragh, H. (december 2000). "Max Planck: Den motvillige revolutionären" . Fysik värld . 13 (12): 31–36. doi : 10.1088/2058-7058/13/12/34 .
- Kramm, Gerhard; Mölders, N. (2009). "Plancks Blackbody Radiation Law: Presentation i olika domäner och bestämning av den relaterade dimensionskonstanten". Journal of the Calcutta Mathematical Society . 5 (1–2): 27–61. arXiv : 0901.1863 . Bibcode : 2009arXiv0901.1863K .
- Kuhn, TS (1978). Svart-kroppsteorin och kvantdiskontinuiteten . Oxford University Press . ISBN 978-0-19-502383-1 .
- Landsberg, PT (1961). Termodynamik med kvantstatistiska illustrationer . Interscience Publishers .
- Landsberg, PT (1978). Termodynamik och statistisk mekanik . Oxford University Press . ISBN 978-0-19-851142-7 .
- Lewis, GN (1926). "Bevarandet av fotoner". Naturen . 118 (2981): 874-875. Bibcode : 1926Natur.118..874L . doi : 10.1038/118874a0 . S2CID 4110026 .
- Loudon, R. (2000). The Quantum Theory of Light (3:e upplagan). Oxford University Press . ISBN 978-0-19-850177-0 .
- Lowen, AN; Blanch, G. (1940). "Tabell över Plancks strålnings- och fotonfunktioner". Journal of the Optical Society of America . 30 (2): 70. Bibcode : 1940JOSA...30...70L . doi : 10.1364/JOSA.30.000070 .
- Lummer, O. ; Kurlbaum, F. (1898). "Der electrisch geglühte "absolut schwarze" Körper und seine Temperaturmessung". Verhandlungen der Deutschen Physikalischen Gesellschaft . 17 : 106–111.
- Lummer, O. ; Pringsheim, E. (1899). "1. Die Vertheilung der Energie in Spectrum des schwarzen Körpers und des blanken Platins; 2. Temperaturbestimmung fester glühender Körper". Verhandlungen der Deutschen Physikalischen Gesellschaft . 1 : 215-235.
- Lummer, O. ; Kurlbaum, F. (1901). "Der elektrisch geglühte "schwarze" Körper" . Annalen der Physik . 310 (8): 829–836. Bibcode : 1901AnP...310..829L . doi : 10.1002/andp.19013100809 .
- Mandel, L .; Wolf, E. (1995). Optisk koherens och kvantoptik . Cambridge University Press . ISBN 978-0-521-41711-2 .
- Mehra, J .; Rechenberg, H. (1982). Den historiska utvecklingen av kvantteorin . Vol. 1. Springer-Verlag . ISBN 978-0-387-90642-3 .
- Messiah, A. (1958). Kvantmekanik . Temmer, GG (övers.). Wiley .
- Michelson, VA (1888). "Teoretisk uppsats om fördelningen av energi i spektra av fasta ämnen" . Filosofisk tidskrift . Serie 5. 25 (156): 425–435. doi : 10.1080/14786448808628207 .
- Mihalas, D .; Weibel-Mihalas, B. (1984). Grunderna för strålningshydrodynamik . Oxford University Press . ISBN 978-0-19-503437-0 .
- Milne, EA (1930). "Stjärnornas termodynamik". Handbuch der Astrophysik . 3 (1): 63–255.
- Mohr, PJ; Taylor, BN; Newell, DB (2012). "CODATA Rekommenderade värden för de grundläggande fysiska konstanterna: 2010" ( PDF) . Recensioner av modern fysik . 84 (4): 1527–1605. arXiv : 1203.5425 . Bibcode : 2012RvMP...84.1527M . CiteSeerX 10.1.1.150.1225 . doi : 10.1103/RevModPhys.84.1527 . S2CID 103378639 .
- Paltridge, GW ; Platt, CMR (1976). Strålningsprocesser inom meteorologi och klimatologi . Elsevier . ISBN 978-0-444-41444-1 .
- Paschen, F. (1895). "Über Gesetzmäßigkeiten in den Spectren fester Körper und über ein neue Bestimmung der Sonnentemperatur". Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen (Mathematisch-Physikalische Klasse) : 294–304.
- Pauli, W. (1973). Enz, CP (red.). Vågmekanik . Margulies, S.; Lewis, HR (översättning). MIT Tryck på . ISBN 978-0-262-16050-6 .
- Planck, M. (1900a). "Über eine Verbesserung der Wien'schen Spectralgleichung" . Verhandlungen der Deutschen Physikalischen Gesellschaft . 2 : 202-204. Översatt i ter Haar, D. (1967). "Om en förbättring av Wiens ekvation för spektrumet" ( PDF) . Den gamla kvantteorin . Pergamon Press . s. 79–81. LCCN 66029628 .
- Planck, M. (1900b). "Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum" . Verhandlungen der Deutschen Physikalischen Gesellschaft . 2 : 237-245. Översatt i ter Haar, D. (1967). "Om teorin om normalspektrumets energifördelningslag" (PDF) . Den gamla kvantteorin . Pergamon Press . sid. 82. LCCN 66029628 .
- Planck, M. (1900c). "Entropie und Temperatur strahlender Wärme" . Annalen der Physik . 306 (4): 719–737. Bibcode : 1900AnP...306..719P . doi : 10.1002/andp.19003060410 .
- Planck, M. (1900d). "Öber irreversibel Strahlungsvorgänge" . Annalen der Physik . 306 (1): 69–122. Bibcode : 1900AnP...306...69P . doi : 10.1002/andp.19003060105 .
- Planck, M. (1901). "Über das Gesetz der Energieverteilung im Normalspektrum" . Annalen der Physik . 4 (3): 553–563. Bibcode : 1901AnP...309..553P . doi : 10.1002/andp.19013090310 . Översatt i Ando, K. "On the Law of Distribution of Energy in the Normal Spectrum" (PDF) . Arkiverad från originalet (PDF) den 6 oktober 2011 . Hämtad 13 oktober 2011 .
- Planck, M. (1906). Vorlesungen über die Theorie der Wärmestrahlung . Johann Ambrosius Barth. LCCN 07004527 .
- Planck, M. (1914). Teorin om värmestrålning . Översatt av Masius, M. (2:a uppl.). P. Blakistons Son & Co. OL 7154661M .
- Planck, M. (1915). Åtta föreläsningar om teoretisk fysik, hölls vid Columbia University 1909 (PDF) . Översatt av Wills, AP New York: Columbia University Press . Hämtad 11 maj 2020 – via Project Gutenberg.
- Planck, M. (1943). "Zur Geschichte der Auffindung des physikalischen Wirkungsquantums". Naturwissenschaften . 31 (14–15): 153–159. Bibcode : 1943NW.....31..153P . doi : 10.1007/BF01475738 . S2CID 44899488 .
- Rayleigh, Lord (1900). "LIII. Anmärkningar om lagen om fullständig strålning" . Filosofisk tidskrift . Serie 5. 49 (301): 539–540. doi : 10.1080/14786440009463878 .
- Rayleigh, Lord (1905). "Den dynamiska teorin om gaser och strålning" . Naturen . 72 (1855): 54–55. Bibcode : 1905Natur..72...54R . doi : 10.1038/072054c0 . S2CID 4057048 .
- Razavy, M. (2011). Heisenbergs kvantmekanik . World Scientific . ISBN 978-981-4304-10-8 .
- Rubens, H .; Kurlbaum, F. (1900a). "Öber die Emission langer Wellen durch den schwarzen Körper". Verhandlungen der Deutschen Physikalischen Gesellschaft . 2 :181.
- Rubens, H .; Kurlbaum, F. (1900b). "Över die Emission langwelliger Wärmestrahlen durch den schwarzen Körper bei verschiedenen Temperaturen". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin : 929–941. Översatt i Rubens, H. ; Kurlbaum, F. (1901). "Om värmestrålningen av långa våglängder som sänds ut av svarta kroppar vid olika temperaturer". The Astrophysical Journal . 14 : 335-348. Bibcode : 1901ApJ....14..335R . doi : 10.1086/140874 .
- Rybicki, GB; Lightman, AP (1979). Strålningsprocesser i astrofysik . John Wiley & Sons . ISBN 978-0-471-82759-7 .
- Sharkov, EA (2003). "Svartkroppsstrålning" (PDF) . Passiv mikrovågsfjärravkänning av jorden . Springer . ISBN 978-3-540-43946-2 .
- Schiff, LI (1949). Kvantmekanik . McGraw-Hill .
- Schirrmacher, A. (2001). Experimenterande teori: bevisen för Kirchhoffs strålningslag före och efter Planck . Münchner Zentrum für Wissenschafts und Technikgeschichte.
- Schwinger, J. (2001). Englert, B.-G. (red.). Kvantmekanik: symbolik för atommätningar . Springer . ISBN 978-3-540-41408-7 .
- Scully, MO ; Zubairy, MS (1997). Kvantoptik . Cambridge University Press . ISBN 978-0-521-43458-4 .
- Siegel, DM (1976). "Balfour Stewart och Gustav Robert Kirchhoff: två oberoende förhållningssätt till "Kirchhoffs strålningslag" " . Isis . 67 (4): 565–600. doi : 10.1086/351669 . PMID 794025 . S2CID 37368520 .
- Siegel, R .; Howell, JR (2002). Thermal Radiation Heat Transfer, Volym 1 (4:e upplagan). Taylor och Francis . ISBN 978-1-56032-839-1 .
- Sommerfeld, A. (1923). Atomstruktur och spektrallinjer . Brose, HL (översättning) (från 3:e tyska uppl.). Methuen .
- Stehle, P. (1994). Ordning, kaos, ordning. Övergången från klassisk till kvantfysik . Oxford University Press . ISBN 978-0-19-507513-7 .
- Stewart, B. (1858). "En redogörelse för några experiment på strålningsvärme" . Transaktioner från Royal Society of Edinburgh . 22 : 1–20. doi : 10.1017/S0080456800031288 . S2CID 122316368 .
- ter Haar, D. (1967). Den gamla kvantteorin . Pergamon Press . LCCN 66-029628 .
- Thornton, ST; Rex, AF (2002). Modern fysik . Thomson Learning . ISBN 978-0-03-006049-6 .
- Tisza, L. (1966). Generaliserad termodynamik . MIT Tryck på .
- Tommasini, D.; Ferrando, F.; Michinel, H.; Seco, M. (2008). "Detektera foton-fotonspridning i vakuum vid exawatt-lasrar". Fysisk granskning A . 77 (1): 042101. arXiv : quant-ph/0703076 . Bibcode : 2008PhRvA..77a2101M . doi : 10.1103/PhysRevA.77.012101 .
- Tyndall, J. (1865a). "Über leuchtende und dunkle Strahlung" . Annalen der Physik und Chemie . 200 (1): 36–53. Bibcode : 1865AnP...200...36T . doi : 10.1002/andp.18652000103 .
- Tyndall, J. (1865b). Värme betraktas som ett rörelsesätt . D. Appleton & Company .
- Wien, W. (1896). "Över die Energievertheilung im Emissionsspectrum eines schwarzen Körpers" . Annalen der Physik und Chemie . 294 (8): 662–669. Bibcode : 1896AnP...294..662W . doi : 10.1002/andp.18962940803 .
- Wilson, AH (1957). Termodynamik och statistisk mekanik . Cambridge University Press .
externa länkar
- Sammanfattning av strålning
- Radiation of a Blackbody – interaktiv simulering för att leka med Plancks lag
- Scienceworld-inlägg om Plancks lag
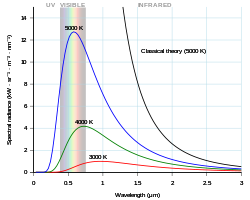















































![{\displaystyle E=\left[3+W\left({\frac {-3}{e^{3}}}\right)\right]k_{\mathrm {B} }T\approx 2.821\ k_{\mathrm {B} }T,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d557a4a8de3b7d175ec1632230e774b325c0fa)
![{\displaystyle E=\left[5+W\left({\frac {-5}{e^{5}}}\right)\right]k_{\mathrm {B} }T\approx 4.965\ k_{\mathrm {B} }T,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7483001560692520562815f31a45e2ec231bba39)





![{\displaystyle E=\left[{\frac {\pi ^{4}}{30\ \zeta (3)}}\right]k_{\mathrm {B} }T\approx 2.701\ k_{\mathrm {B} }T,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/538cd5d72259f8da2c70a860fdc3231a0df5a1e5)











































