Lambert W funktion

Produktlogaritmen Lambert W-funktionen plottad i det komplexa planet från −2 − 2 i till 2 + 2 i

Grafen för y = W ( x ) för reella x < 6 och y > −4 . Den övre grenen (blå) med y ≥ −1 är grafen för funktionen W ₀ (huvudgren), den nedre grenen (magenta) med y ≤ −1 är grafen för funktionen W ₋₁ . Minsta värdet på x är {−1/ e ,−1}

Inom matematiken är Lambert w W -funktionen , även kallad omega-funktionen eller produktlogaritmen f ( w ) = we ^, en flervärdig funktion , nämligen grenarna av den omvända relationen till funktionen , där w är vilket komplext tal som helst och e ^w är exponentialfunktionen . _

För varje heltal k finns det en gren, betecknad med W _k ​​( z ) , som är en komplext värderad funktion av ett komplext argument. W ₀ är känd som huvudgrenen . Dessa funktioner har följande egenskap: om z och w är några komplexa tal, då

$we^{w}=z$

håller om och bara om

$w=W_{k}(z)\ \ {\text{ för något heltal }}k.$

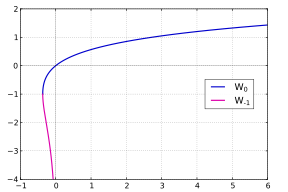
När det bara handlar om reella tal räcker det med de två grenarna W ₀ och W ₋₁ : för reella tal x och y ekvationen

$ye^{y}=x$

kan endast lösas för y om x ≥ − 1 / e ; vi får ₀ y = W ( x ) om x ≥ 0 och de två värdena ₀ y = W ( x ) och y = W ₋₁ ( x ) om − 1 / e ≤ x < 0 .

Lambert W -relationen kan inte uttryckas i termer av elementära funktioner . Det är användbart i kombinatorik , till exempel vid uppräkning av träd . Det kan användas för att lösa olika ekvationer som involverar exponentialer (t.ex. maxima för Planck- , Bose-Einstein- och Fermi-Dirac- distributionerna) och förekommer även i lösningen av fördröjningsdifferentialekvationer , såsom y ′( t ) = a y ( t − 1) . Inom biokemi , och i synnerhet enzymkinetik , beskrivs en lösning i öppen form för tidsförloppskinetikanalys av Michaelis-Menten-kinetiken i termer av Lambert W -funktionen.

Huvudgrenen av Lambert W -funktionen i det komplexa planet, plottad med domänfärgning . Notera grenen som skärs längs den negativa reella axeln, som slutar på − 1 / e .

Modulen för huvudgrenen av Lambert W -funktionen, färgad enligt arg W ( z )

Terminologi

Lambert W -funktionen är uppkallad efter Johann Heinrich Lambert . Huvudgrenen W ₀ betecknas Wp i Digital Library of Mathematical Functions och grenen W ₋₁ betecknas där Wm .

Notationskonventionen som väljs här (med W ₀ och W ₋₁ ) följer den kanoniska referensen på Lambert W -funktionen av Corless, Gonnet, Hare, Jeffrey och Knuth .

Namnet "produktlogaritm" kan förstås så här: Eftersom den . ^inversa funktionen av f ( w ) = e ^w kallas logaritmen , är det vettigt att kalla produktens inversa "funktion" för "produktlogaritm" (Teknisk anmärkning: liksom den komplexa logaritmen är den flervärdig och W beskrivs därför som den omvända relationen snarare än den inversa funktionen.) Den är relaterad till Omega-konstanten , vilket är lika med ₀ W (1) .

Historia

Lambert övervägde först den relaterade Lamberts transcendentala ekvation 1758, vilket ledde till en artikel av Leonhard Euler 1783 som diskuterade det speciella fallet med vi ^w .

Ekvationen som Lambert ansåg var

$x=x^{m}+q.$

Euler omvandlade denna ekvation till formen

$x^{a}-x^{b}=(ab)cx^{a+b}.$

Båda författarna härledde en serielösning för sina ekvationer.

När Euler hade löst denna ekvation ansåg han fallet a = b . Han tog gränser och härledde ekvationen

$\ln x=cx^{a}.$

Han satte sedan a = 1 och fick en konvergent serielösning för den resulterande ekvationen, uttryckande x i termer av c .

Efter att ha tagit derivator med avseende på x och viss manipulation erhålls standardformen för Lambert-funktionen.

1993 rapporterades det att Lambert W -funktionen ger en exakt lösning på den kvantmekaniska dubbelbrunnars Dirac deltafunktionsmodell för lika laddningar - ett grundläggande problem inom fysiken. På grund av detta insåg Rob Corless och utvecklare av Maple- datoralgebrasystemet att "Lambert W-funktionen har använts i stor utsträckning inom många områden, men på grund av olika notation och frånvaron av ett standardnamn var medvetenheten om funktionen inte lika hög. som det borde ha varit."

Ett annat exempel där denna funktion finns är i Michaelis–Menten kinetik .

Även om det ansågs allmänt att Lambert W -funktionen inte kan uttryckas i termer av elementära ( Liouvillian ) funktioner, dök det första publicerade beviset inte upp förrän 2008.

Elementära egenskaper, grenar och utbud

Räckvidden för W -funktionen, som visar alla grenar. De svarta kurvorna (inklusive den verkliga axeln) utgör bilden av den verkliga axeln, de orangea kurvorna är bilden av den imaginära axeln. Den lila kurvan är bilden av en liten cirkel runt punkten z = 0 ; de röda kurvorna är bilden av en liten cirkel runt punkten z = − 1 / e .

Plotta den imaginära delen av W[n,x+iy] för grenar n=-2,-1,0,1,2. Plottet liknar det för den flervärdiga komplexa logaritmfunktionen förutom att avståndet mellan ark inte är konstant och anslutningen av huvudarket är annorlunda

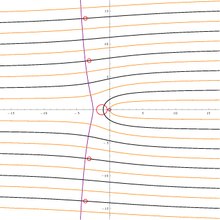
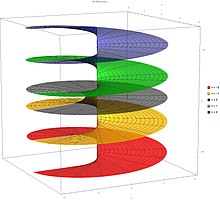
Det finns oräkneligt många grenar av W -funktionen, betecknade med W _k ​​( z ) , för heltal k ; ₀ W ( z ) är huvudgrenen (eller huvudgrenen). ₀ W ( z ) definieras för alla komplexa tal z medan Wk _. ( z ) med k ≠ 0 är definierade för alla icke-noll z Vi har ₀ W (0) = 0 och lim z →0 W _k ( z ) = −∞ för alla k ≠ 0 .

Grenpunkten för huvudgrenen är vid z = − 1 / e , med ett grensnitt som sträcker sig till −∞ längs den negativa reella axeln. Detta grensnitt skiljer huvudgrenen från de två grenarna W ₋₁ och W ₁ . I alla grenar W _k med k ≠ 0 , finns det en grenpunkt vid z = 0 och en gren skuren längs hela den negativa reella axeln.

Funktionerna W _k ( z ), k ∈ Z är alla injektiva och deras intervall är disjunkta. Omfånget för hela den flervärdiga funktionen W är det komplexa planet. Bilden av den reella axeln är föreningen av den reella axeln och quadratrixen av Hippias , den parametriska kurvan w = − t cot t + it .

Omvänd

Regioner i det komplexa planet för vilka ${\displaystyle W(n,ze^{z})=z} ,$ där z = x + iy . De mörkare gränserna för en viss region ingår i den ljusare regionen av samma färg. Punkten vid {−1, 0} ingår i både $n=-1$ (blå) regionen och $n=0$ (grå) region. Horisontella rutnätslinjer är i multiplar av π .

Avståndsdiagrammet ovan avgränsar också områdena i det komplexa planet där det enkla inversa förhållandet $W(n,ze^{z})=z$ är sant. f = ze ^z antyder att det finns ett n så att ${\displaystyle z=W(n,f)=W(n,ze^{z})} ,$ där n beror på värdet av z . Värdet på heltal n ändras abrupt när ze ^z är vid grensnittet av ${\displaystyle W(n,ze^{z})} ,$ vilket betyder att ze ^z ≤ 0 , förutom för $n=0$ där det är ze ^z ≤ −1/ e .

Om du definierar ${\displaystyle z=x+iy} ,$ där x och y är reella, och uttrycker e ^z i polära koordinater, ser man att

${\begin{aligned}ze^{z}&=(x+iy)e^{x}(\cos y+i\sin y)\\&=e^{x}(x\cos yy \sin y)+ie^{x}(x\sin y+y\cos y).\\\end{aligned}}$

För ${\displaystyle n\neq 0} är$ grensnittet för $W(n,ze^{z})$ den icke-positiva reella axeln, så att

$x\sin y+y\cos y=0\Högerpil x=-y/\tan(y),$

och

$(x\cos yy\sin y)e^{x}\leq 0.$

För $n=0$ är grensnittet för $W[n,ze^{z}]$ den reella axeln med $-\infty <z\leq -1/e$ , så att ojämlikheten blir

$(x\cos yy\sin y)e^{x}\leq -1/e.$

Inom de regioner som avgränsas av ovanstående finns inga diskontinuerliga förändringar i $W(n,ze^{z})$ , och de regionerna anger var W - funktionen helt enkelt är inverterbar, dvs. $W(n,ze^{z})=z$ .

Kalkyl

Derivat

Genom implicit differentiering kan man visa att alla grenar av W uppfyller differentialekvationen

$z(1+W){\frac {dW}{dz}}=W\quad {\text{för }}z\neq -{\frac {1}{e}}.$

( W är inte differentierbar för z = − 1 / e .) Som en konsekvens får vi följande formel för derivatan av W :

${\frac {dW}{dz}}={\frac {W(z)}{z(1+W(z))}}\quad {\text{för }}z\inte \in \ vänster\{0,-{\frac {1}{e}}\höger\}.$

Med hjälp av identiteten e ^{W ( z )} = z / W ( z ) får vi följande ekvivalenta formel:

${\frac {dW}{dz}}={\frac {1}{z+e^{W(z)}}}\quad {\text{för }}z\neq -{\frac { 1}{e}}.$

Vid det ursprung vi har

$W'_{0}(0)=1.$

Väsentlig

Funktionen W ( x ) , och många andra uttryck som involverar W ( x ) , kan integreras med hjälp av substitutionen w = W ( x ) , dvs x = we ^w :

${\begin{aligned}\int W(x)\,dx&=xW(x)-x+e^{W(x)}+C\\&=x\left(W(x)-1 +{\frac {1}{W(x)}}\right)+C.\end{aligned}}$

(Den sista ekvationen är vanligare i litteraturen men är odefinierad vid x = 0 ). En konsekvens av detta (om man använder det faktum att ₀ W ( e ) = 1 ) är identiteten

$\int _{0}^{e}W_{0}(x)\,dx=e-1.$

Asymptotiska expansioner

Taylor -serien av W ₀ runt 0 kan hittas med hjälp av Lagranges inversionssats och ges av

$W_{0}(x)=\summa _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}x^{n}= xx^{2}+{\tfrac {3}{2}}x^{3}-{\tfrac {8}{3}}x^{4}+{\tfrac {125}{24}}x^ {5}-\cdots .$

Konvergensradien är 1 / e , vilket framgår av förhållandetestet . Funktionen som definieras av denna serie kan utökas till en holomorf funktion definierad på alla komplexa tal med en gren skuren längs intervallet (−∞, − 1 / e ] ; denna holomorfa funktion definierar huvudgrenen av Lambert W -funktionen.

För stora värden på x är W ₀ asymptotisk till

${\begin{aligned}W_{0}(x)&=L_{1}-L_{2}+{\frac {L_{2}}{L_{ 1}}}+{\frac {L_{2}\left(-2+L_{2}\right)}{2L_{1}^{2}}}+{\frac {L_{2}\left( 6-9L_{2}+2L_{2}^{2}\höger)}{6L_{1}^{3}}}+{\frac {L_{2}\left(-12+36L_{2}- 22L_{2}^{2}+3L_{2}^{3}\höger)}{12L_{1}^{4}}}+\cdots \\[5pt]&=L_{1}-L_{2 }+\summa _{l=0}^{\infty }\summa _{m=1}^{\infty }{\frac {(-1)^{l}\left[{\begin{smallmatrix}l +m\\l+1\end{smallmatrix}}\right]}{m!}}L_{1}^{-lm}L_{2}^{m},\end{aligned}}$

där L ₁ = ln x , L ₂ = ln ln x , och [
^{l + m} _{l + 1} ] är ett icke-negativt stirlingtal av det första slaget . Med endast de två första termerna av expansionen,

$W_{0}(x)=\ln x-\ln \ln x+{\mathcal {o}}(1).$

Den andra reella grenen, W ₋₁ , definierad i intervallet [− 1 / e , 0) , har en approximation av samma form som x närmar sig noll, med i detta fall L ₁ = ln(− x ) och L ₂ = ln(−ln(− x )) .

Heltal och komplexa potenser

Heltalspotens för W ₀ medger också enkla Taylor (eller Laurent ) serieexpansioner vid noll:

$W_{0}(x)^{2}=\summa _{n=2}^{\infty }{\frac {-2\left(-n\right)^{n-3}}{ (n-2)!}}x^{n}=x^{2}-2x^{3}+4x^{4}-{\tfrac {25}{3}}x^{5}+18x^ {6}-\cdots .$

Mer allmänt, för r ∈ Z , ger Lagrange-inversionsformeln

$W_{0}(x)^{r}=\summa _{n=r}^{\infty }{\frac {-r\left(-n\right)^{nr-1 }}{(nr)!}}x^{n},$

som i allmänhet är en Laurent-serie av order r . På motsvarande sätt kan det senare skrivas i form av en Taylor-expansion av potenserna ₀ W ( x ) / x :

$\left({\frac {W_{0}(x)}{x}}\right)^{r}=e^{-rW_{0}(x)}=\ summa _{n=0}^{\infty }{\frac {r\left(n+r\right)^{n-1}}{n!}}\left(-x\right)^{n} ,$

som gäller för alla r ∈ C och | x | < 1 / e .

Gränser och ojämlikheter

Ett antal icke-asymptotiska gränser är kända för Lambert-funktionen.

Hoorfar och Hassani visade att följande gräns gäller för x ≥ e :

$\ln x-\ln \ln x+{\frac {\ln \ln x}{2\ln x}}\leq W_{0}(x)\leq \ln x-\ln \ln x+{ \frac {e}{e-1}}{\frac {\ln \ln x}{\ln x}}.$

De visade också den allmänna gränsen

$W_{0}(x)\leq \log \left({\frac {x+y}{1+\log (y)}}\höger),$

för varje $y>1/e$ och $x\geq -1/e$ , med likhet endast för $x=y\log(y)$ . Bindningen gör att många andra gränser kan göras, som att ta $y=x+1$ som ger gränsen

$W_{0}(x)\leq \log \left({\frac {2x+1}{1+\log(x+1)}}\right).$

2013 bevisades att grenen W ₋₁ kan avgränsas enligt följande:

$-1-{\sqrt {2u}}-u< W_{-1}\left(-e^{-u-1}\right)<-1-{\sqrt {2u}}-{\tfrac {2}{3}}u\quad {\text{för }}u>0.$

Roberto Iacono och John P. Boyd utökade gränserna enligt följande:

$\ln \left({\frac {x}{\ln x}}\right)-{\frac {\ln \left({\frac {x}{\ln x}}\right)}{ 1+\ln \left({\frac {x}{\ln x}}\höger)}}\ln \left(1-{\frac {\ln \ln x}{\ln x}}\höger) \leq W_{0}(x)\leq \ln \left({\frac {x}{\ln x}}\höger)-\ln \left(\left(1-{\frac {\ln \ln x}{\ln x}}\right)\left(1-{\frac {\ln \left(1-{\frac {\ln \ln x}{\ln x}}\right)}{1+ \ln \left({\frac {x}{\ln x}}\right)}}\right)\right).$

Identiteter

En plot av W _j ( x e ^x ) där blå är för j =0 och röd är för j =−1. Den diagonala linjen representerar intervallen där W _j ( x e ^x )= x

Produktlogaritmen Lambert W-funktionen W 2(z) plottad i det komplexa planet från -2-2i till 2+2i

Några få identiteter följer av definitionen:

${\begin{aligned}W_{0}(xe^{x}) &=x&{\text{för }}x&\geq -1,\\W_{-1}(xe^{x})&=x&{\text{för }}x&\leq -1.\end{aligned }}$

Observera att eftersom f ( x ) = xe ^x inte är injektiv , gäller det inte alltid att W ( f ( x )) = x , ungefär som med de inversa trigonometriska funktionerna . För fixerad x < 0 och x ≠ −1 har ekvationen xe ^x = ye ^y två reella lösningar i y , varav den ena naturligtvis är y = x . Då, för i = 0 och x < −1 , liksom för i = −1 och x ∈ (−1, 0) , är y = W _i ( xe ^x ) den andra lösningen.

Några andra identiteter:

${\displaystyle {\begin{aligned}&W(x)e^{W(x)}=x,\quad {\text{därför:}}\\[5pt]&e^{W(x)}={\ frac {x}{W(x)}},\qquad e^{-W(x)}={\frac {W(x)}{x}},\qquad e^{nW(x)}=\ left({\frac {x}{W(x)}}\right)^{n}.\end{aligned}}} ln$

$\ln W_{0}(x)=\ln x-W_{0}(x)\quad {\text{for }}x>0.$

$W_{0}\left(x\ln x\right)=\ln x\quad {\text{and}}\quad e^{W_{0}\left(x\ln x\right)} =x\quad {\text{för }}{\frac {1}{e}}\leq x.$

$W_{-1}\left(x\ln x\right)=\ln x\quad {\text{and}}\quad e^{W_{-1}\left(x\ln x\right )}=x\quad {\text{för }}0<x\leq {\frac {1}{e}}.$

${\displaystyle {\begin{aligned}&W(x)=\ln {\frac {x}{W(x)}}&&{\text{för } }x\geq -{\frac {1}{e}},\\[5pt]&W\left({\frac {nx^{n}}{W\left(x\right)^{n-1} }}\right)=nW(x)&&{\text{för }}n,x>0\end{aligned}}} ($

som kan utökas till andra n och x om rätt gren väljs).

$W(x)+W(y)=W\left(xy\left({\frac {1 }{W(x)}}+{\frac {1}{W(y)}}\right)\right)\quad {\text{för }}x,y>0.$

Ersätter −ln x i definitionen:

${\begin{aligned}W_{0}\left(-{\frac {\ln x}{x}}\right)&=-\ln x&{\text{för }}0&<x\leq e,\\[5pt]W_{-1}\left(-{\frac {\ln x}{x}}\right)&=-\ln x&{\text{för }}x&>e.\end {Justerat}}$

Med Eulers itererade exponentiella h ( x ) :

${\begin{aligned}h(x)&=e^{- W(-\ln x)}\\&={\frac {W(-\ln x)}{-\ln x}}\quad {\text{för }}x\neq 1.\end{aligned} }$

Särskilda värden

Följande är speciella värden för huvudgrenen:

${\displaystyle W\left(-{\frac {\pi }{2}}\right)={\frac {i\pi}{2}}.} W ($

$displaystyle W\left(-{\frac {1}{e}}\right)=-1.}$

$W\left(2\ln 2\right)= \ln 2.$

${\displaystyle W\left(x\ln x\right)=\ln x\ {\text{ tillhandahållen }}\ x\geqslant 1/e\approx 0,36788.} W ( ) = 0.$

$0 )=0.}$

$W(1)=\Omega =\left(\int _{-\infty }^{\infty }{\frac {dt}{\left(e^{t} -t\right)^{2}+\pi ^{2}}}\right)^{-1}-1\approx 0,56714329\ldots$ ( omega-konstanten ).

$W(1)=e^{-W(1)}=\ln \left({\frac {1}{W(1)}}\right)=-\ln W(1).$

$W(e)=1.$

$W\left(e^{1+e}\right)=e.$

$W(-1)\approx -0,31813+1,33723i.$

Framställningar

Huvudgrenen av Lambert-funktionen kan representeras av en riktig integral, på grund av Poisson:

$-{\frac {\pi }{2}}W(-x)=\int _{0}^{\pi }{\frac {\sin \left({\tfrac {3}{2} }t\right)-xe^{\cos t}\sin \left({\tfrac {5}{2}}t-\sin t\right)}{1-2xe^{\cos t}\cos( t-\sin t)+x^{2}e^{2\cos t}}}\sin \left({\tfrac {1}{2}}t\right)\,dt\quad {\text{ för }}|x|<{\frac {1}{e}}.$

På den bredare domänen − 1 / e ≤ x ≤ e , hittades den betydligt enklare representationen av Mező:

$W(x)={\frac {1}{\pi }}\operatörsnamn {Re} \int _{0}^{\pi }\ln \left({\frac {e^{e^{ it}}-xe^{-it}}{e^{e^{it}}-xe^{it}}}\right)\,dt.$

En annan representation av huvudgrenen hittades av samma författare och tidigare av Kalugin-Jeffrey-Corless:

$W(x)={\frac {1}{\pi }}\int _{0}^{\pi }\log \left(1+x{\frac {\sin t}{t}} e^{t\cot t}\right)dt.$

Följande fortsatta bråkrepresentation gäller även för huvudgrenen:

$W(x)={\cfrac {x}{1+{\cfrac {x}{1+{\cfrac {x}{2+{\cfrac {5x}{3+{\cfrac {17x} {10+{\cfrac {133x}{17+{\cfrac {1927x}{190+{\cfrac {13582711x}{94423+\ddots }}}}}}}}}}}}}}}.$

Även om | W ( x ) | < 1 :

$W(x)={\cfrac {x}{\exp {\cfrac {x}{\exp {\cfrac {x}{\ddots }}}}}}.$

I sin tur, om | W ( x ) | >e , då

$W(x)=\ln {\cfrac {x}{\ln {\cfrac {x}{\ln {\cfrac {x}{\ddots }}}}}}.$

Andra formler

Bestämda integraler

Det finns flera användbara definitiva integralformler som involverar huvudgrenen av W -funktionen, inklusive följande:

${\begin{aligned}&\int _{0}^{\pi}W\left(2\cot ^{2}x\right)\sec ^{2}x\,dx=4{\ sqrt {\pi }}.\\[5pt]&\int _{0}^{\infty }{\frac {W(x)}{x{\sqrt {x}}}}\,dx=2{ \sqrt {2\pi }}.\\[5pt]&\int _{0}^{\infty }W\left({\frac {1}{x^{2}}}\right)\,dx ={\sqrt {2\pi }}.\end{aligned}}$

Den första identiteten kan hittas genom att skriva den Gaussiska integralen i polära koordinater .

Den andra identiteten kan härledas genom att göra substitutionen u = W ( x ) , vilket ger

${\begin{aligned}x&=ue^{u},\\[5pt]{\frac {dx}{du}}&=(u+1)e^{u}.\end{aligned} }$

Således

${\begin{aligned}\int _{0}^{\infty }{\frac {W(x)}{x{\sqrt {x}}}}\,dx&=\int _{0} ^{\infty }{\frac {u}{ue^{u}{\sqrt {ue^{u}}}}}(u+1)e^{u}\,du\\[5pt]&= \int _{0}^{\infty }{\frac {u+1}{\sqrt {ue^{u}}}}du\\[5pt]&=\int _{0}^{\infty } {\frac {u+1}{\sqrt {u}}}{\frac {1}{\sqrt {e^{u}}}}du\\[5pt]&=\int _{0}^{ \infty }u^{\tfrac {1}{2}}e^{-{\frac {u}{2}}}du+\int _{0}^{\infty }u^{-{\tfrac { 1}{2}}}e^{-{\frac {u}{2}}}du\\[5pt]&=2\int _{0}^{\infty }(2w)^{\tfrac { 1}{2}}e^{-w}\,dw+2\int _{0}^{\infty }(2w)^{-{\tfrac {1}{2}}}e^{-w }\,dw&&\quad (u=2w)\\[5pt]&=2{\sqrt {2}}\int _{0}^{\infty }w^{\tfrac {1}{2}}e ^{-w}\,dw+{\sqrt {2}}\int _{0}^{\infty }w^{-{\tfrac {1}{2}}}e^{-w}\,dw \\[5pt]&=2{\sqrt {2}}\cdot \Gamma \left({\tfrac {3}{2}}\right)+{\sqrt {2}}\cdot \Gamma \left( {\tfrac {1}{2}}\right)\\[5pt]&=2{\sqrt {2}}\left({\tfrac {1}{2}}{\sqrt {\pi }}\ höger)+{\sqrt {2}}\left({\sqrt {\pi }}\right)\\[5pt]&=2{\sqrt {2\pi }}.\end{aligned}}$

Den tredje identiteten kan härledas från den andra genom att göra substitutionen u = x ⁻² och den första kan också härledas från den tredje genom substitutionen z = 1 / √ 2 tan x .

Förutom z längs grensnittet (−∞, − 1 / e ] (där integralen inte konvergerar), kan huvudgrenen av Lambert W -funktionen beräknas med följande integral:

${\begin{aligned}W(z)&={\frac {z}{2\pi }}\int _{-\ pi }^{\pi }{\frac {\left(1-\nu \cot \nu \right)^{2}+\nu ^{2}}{z+\nu \csc \nu e^{-\ nu \cot \nu }}}\,d\nu \\[5pt]&={\frac {z}{\pi }}\int _{0}^{\pi }{\frac {\left(1 -\nu \cot \nu \right)^{2}+\nu ^{2}}{z+\nu \csc \nu e^{-\nu \cot \nu }}}\,d\nu ,\ end{aligned}}$

där de två integraluttrycken är ekvivalenta på grund av integrandens symmetri.

Obestämda integraler

$$\int {\frac {W(x)}{x}}\,dx\;=\;{\ frac {W(x)^{2}}{2}}+W(x)+C$$

1:a beviset

Introducera substitutionsvariabel $u=W(x)\rightarrow ue^{u}=x\;\ ;\;\;{\frac {d}{du}}ue^{u}=(u+1)e^{u}$

$\int {\frac {W(x)}{x}}\,dx\;=\;\ int {\frac {u}{ue^{u}}}(u+1)e^{u}\,du$

$\int {\frac {W(x)}{x}}\,dx\;=\;\int {\frac {\cancel {\color {OliveGreen}{u}}}{{\cancel { \color {OliveGreen}{u}}}{\cancel {\color {BrickRed}{e^{u}}}}}}\left(u+1\right){\cancel {\color {BrickRed}{e ^{u}}}}\,du$

$\int {\frac {W(x)}{x}}\,dx\;= \;\int u+1\,du$

$\int {\frac {W(x)}{x}}\,dx\;=\;{\frac {u^{2}}{2}}+u+C$

$u=W(x)$

$\int {\frac {W(x)}{x }}\,dx\;=\;{\frac {W(x)^{2}}{2}}+W(x)+C$

2:a beviset

$W(x)e^{W(x)}=x\högerpil {\frac {W(x) )}{x}}=e^{-W(x)}$

$\int {\frac {W(x)}{x}}\,dx\;=\;\int e^{- W(x)}\,dx$

$u=W(x)\högerpil ue^{u}=x\;\;\; \;{\frac {d}{\,du}}ue^{u}=\left(u+1\right)e^{u}$

$\int {\frac {W(x)}{x}}\,dx\;=\;\int e^{-u}(u+1)e^{u}\,du$

$\int {\frac {W(x)}{x}}\,dx\;=\;\int {\avbryt {\color {OliveGreen}{e^{-u}}}}\left(u+1\right){\cancel {\color {OliveGreen}{e^{u}}}}\,du$

$\int {\frac {W(x)}{x}}\,dx\;=\;\int u+1\,du$

$\int {\frac {W(x)}{x}}\,dx\;=\;{\frac {u^{2 }}{2}}+u+C$

$u=W(x)$

$\int {\frac {W(x)}{x}}\,dx\;=\;{\ frac {W(x)^{2}}{2}}+W(x)+C$

$$\int W\left(Ae^{Bx}\right)\ ,dx\;=\;{\frac {W\left(Ae^{Bx}\right)^{2}}{2B}}+{\frac {W\left(Ae^{Bx}\right)} {B}}+C$$

Bevis

$\int W\left(Ae^{Bx}\right)\,dx\;=\;\int W\ vänster(Ae^{Bx}\höger)\,dx$

$u=Bx\högerpil {\frac {u}{B}}=x\;\;\;\;{\frac {d }{du}}{\frac {u}{B}}={\frac {1}{B}}$

$\int W\left(Ae^{Bx}\right)\,dx\;=\;\int W \left(Ae^{u}\right){\frac {1}{B}}du$

$v=e^{u}\högerpil \ln \left(v\right)=u\;\; \;\;{\frac {d}{dv}}\ln \left(v\right)={\frac {1}{v}}$

$\int W\left(Ae^{Bx}\right)\,dx\;=\;{\frac {1}{B}}\int {\frac {W\left(Av\right)}{v}}dv$

$w=Av\rightarrow {\frac {w}{A}}=v\;\;\;\;{\frac {d }{dw}}{\frac {w}{A}}={\frac {1}{A}}$

$\int W\left(Ae^{Bx}\right)\,dx\;=\;{ \frac {1}{B}}\int {\frac {{\cancel {\color {OliveGreen}{A}}}W(w)}{w}}{\cancel {\color {Olivgrön}{\frac {1}{A}}}}dw$

$t=W\left(w\right)\rightarrow te^{t}=w\; \;\;\;{\frac {d}{dt}}te^{t}=\left(t+1\right)e^{t}$

$\int W\left(Ae^{Bx}\right)\,dx\;= \;{\frac {1}{B}}\int {\frac {t}{te^{t}}}\left(t+1\right)e^{t}dt$

$\int W\left(Ae^{Bx}\right)\,dx\;= \;{\frac {1}{B}}\int {\frac {\cancel {\color {OliveGreen}{t}}}{{\cancel {\color {OliveGreen}{t}}}{\cancel { \color {BrickRed}{e^{t}}}}}}\left(t+1\right){\cancel {\color {BrickRed}{e^{t}}}}dt$

$\int W\left(Ae^{Bx}\right)\,dx\;=\;{\frac {1} {B}}\int t+1dt$

$\int W\left(Ae^{Bx}\right)\,dx\;=\;{\frac {t ^{2}}{2B}}+{\frac {t}{B}}+C$

$t=W\left(w\right)$

$\int W\left(Ae^{Bx}\right)\,dx\;=\ ;{\frac {W\left(w\right)^{2}}{2B}}+{\frac {W\left(w\right)}{B}}+C$

$w=Av$

$\int W\left(Ae^{Bx}\right)\,dx\; =\;{\frac {W\left(Av\right)^{2}}{2B}}+{\frac {W\left(Av\right)}{B}}+C$

$v=e^{u}$

$\int W\left(Ae^{Bx}\right)\,dx \;=\;{\frac {W\left(Ae^{u}\right)^{2}}{2B}}+{\frac {W\left(Ae^{u}\right)}{B }}+C$

$u=Bx$

$\int W\left(Ae^{Bx}\right)\ ,dx\;=\;{\frac {W\left(Ae^{Bx}\right)^{2}}{2B}}+{\frac {W\left(Ae^{Bx}\right)} {B}}+C$

$$\int {\frac {W(x)}{x^{2}}} \,dx\;=\;\operatörsnamn {Ei} \left(-W(x)\right)-e^{-W(x)}+C$$

Bevis

Introducera substitutionsvariabel $u=W(x)$ , vilket ger oss $ue^{u}=x$ och ${\frac {d}{du}}ue^{u}=\left(u+1\right)e^{u}$

${\begin{aligned}\int {\frac {W(x)}{x^{2}}}\,dx\;&= \;\int {\frac {u}{\left(ue^{u}\right)^{2}}}\left(u+1\right)e^{u}du\\&=\;\ int {\frac {u+1}{ue^{u}}}du\\&=\;\int {\frac {u}{ue^{u}}}du\;+\;\int {\ frac {1}{ue^{u}}}du\\&=\;\int e^{-u}du\;+\;\int {\frac {e^{-u}}{u}} du\end{aligned}}$

$v=-u\rightarrow -v=u\;\;\;\;{\frac {d}{dv}}-v =-1$

$\int {\frac {W(x)}{x^{2}}}\ ,dx\;=\;\int e^{v}\left(-1\right)dv\;+\;\int {\frac {e^{-u}}{u}}du$

$\int {\frac {W(x)}{x^{2}}}\,dx\;= \;-e^{v}+\operatörsnamn {Ei} \left(-u\right)+C$

$v=-u$

$\int {\frac {W(x)}{x^{2}}}\,dx\; =\;-e^{-u}+\operatörsnamn {Ei} \left(-u\right)+C$

$u=W(x)$

${\begin{aligned}\int {\frac {W(x)}{x^{2}}}\,dx\;&=\;-e^{-W(x)}+\operatörsnamn {Ei} \left(-W(x)\right)+C\\&=\;\operatörsnamn {Ei} \left(-W(x)\right)-e^{-W(x)}+C \end{aligned}}$

Ansökningar

Lösa ekvationer

Lambert W -funktionen används för att lösa ekvationer där den okända kvantiteten förekommer både i basen och i exponenten, eller både inom och utanför en logaritm. Strategin är att konvertera en sådan ekvation till en av formen ze ^z = w och sedan lösa för z med hjälp av W -funktionen.

Till exempel ekvationen

$3^{x}=2x+2$

(där x är ett okänt reellt tal) kan lösas genom att skriva om det som

${\begin{aligned}&(x+1)\ 3^{-x}= {\frac {1}{2}}&({\mbox{multiplicera med }}3^{-x}/2)\\\Leftrightarrow \ &(-x-1)\ 3^{-x-1} =-{\frac {1}{6}}&({\mbox{multiplicera med }}{-}1/3)\\\Vänsterhögerpil \ &(\ln 3)(-x-1)\ e^{ (\ln 3)(-x-1)}=-{\frac {\ln 3}{6}}&({\mbox{multiplicera med }}\ln 3)\end{aligned}}$

Denna sista ekvation har den önskade formen och lösningarna för verkligt x är:

$(\ln 3 )(-x-1)=W_{0}\left({\frac {-\ln 3}{6}}\right)\ \ \ {\textrm {eller}}\ \ \ (\ln 3)( -x-1)=W_{-1}\left({\frac {-\ln 3}{6}}\right)$

och sålunda:

$x=-1-{\frac {W_{0}\left(-{\frac {\ln 3}{6}}\right)}{\ln 3}}=-0,79011\ldots \ \ { \textrm {eller}}\ \ x=-1-{\frac {W_{-1}\left(-{\frac {\ln 3}{6}}\right)}{\ln 3}}=1,44456 \ldots$

Generellt är lösningen på

$x=a+b\,e^{cx}$

är:

$x=a-{\frac {1}{c}}W(-bc\,e^{ac})$

där a , b och c är komplexa konstanter, där b och c inte är lika med noll, och W -funktionen är av valfri heltalsordning.

Viskösa flöden

Granulära och skräpflödesfronter och avlagringar, och fronterna av viskösa vätskor i naturliga händelser och i laboratorieexperiment kan beskrivas genom att använda Lambert–Eulers omega-funktion enligt följande:

$H(x)=1+W\left((H(0)-1 )e^{(H(0)-1)-{\frac {x}{L}}}\höger),$

där H ( x ) är skräpflödeshöjden, x är kanalen nedströms, L är den enhetliga modellparametern som består av flera fysiska och geometriska parametrar för flödet, flödeshöjden och den hydrauliska tryckgradienten.

I rörflöde är Lambert W-funktionen en del av den explicita formuleringen av Colebrook-ekvationen för att hitta Darcy-friktionsfaktorn . Denna faktor används för att bestämma tryckfallet genom ett rakt rör när flödet är turbulent .

Tidsberoende flöde i enkla grenhydrauliksystem

Den huvudsakliga grenen av Lambert W -funktionen användes inom området maskinteknik , i studien av tidsberoende överföring av newtonska vätskor mellan två reservoarer med varierande fria ytnivåer, med användning av centrifugalpumpar. Lambert W -funktionen gav en exakt lösning på vätskeflödet i både laminära och turbulenta regimer:

$${\begin{aligned}Q_{\text{turb}}&={\frac {Q_{i}}{\zeta _{i}}}W_{0}\left[\zeta _{i} \,e^{(\zeta _{i}+\beta t/b)}\right]\\Q_{\text{lam}}&={\frac {Q_{i}}{\xi _{i }}}W_{0}\left[\xi _{i}\,e^{\left(\xi _{i}+\beta t/(b-\Gamma _{1})\right)}\ höger]\end{aligned}}$$

där $Q_{i}$ är den initiala flödeshastigheten och $t$ är tid.

Neuroimaging

Lambert W -funktionen användes inom området neuroimaging för att länka cerebralt blodflöde och syreförbrukningsförändringar inom en hjärnvoxel, till motsvarande blodsyresättningsnivåberoende (BOLD) signal.

Kemiteknik

Lambert W -funktionen användes inom området kemiteknik för att modellera den porösa elektrodfilmtjockleken i en glasartad kolbaserad superkondensator för elektrokemisk energilagring. Lambert W -funktionen visade sig vara den exakta lösningen för en termisk aktiveringsprocess i gasfas där tillväxt av kolfilm och förbränning av samma film konkurrerar med varandra.

Kristalltillväxt

I kristalltillväxten kan fördelningen av löst ämne erhållas genom att använda Scheil-ekvationen . Så den negativa principen för Lambert W-funktionen kan användas för att beräkna fördelningskoefficienten, ${\textstyle k}$ :

${\begin{aligned}&k={\frac {W( Z)}{\ln(1-fs)}}\\&Z={\frac {C_{S}}{C_{0}}}(1-fs)\ln(1-fs)\end{aligned} }$

Materialvetenskap

Lambert W -funktionen användes inom området för epitaxiell filmtillväxt för bestämning av filmtjockleken på den kritiska dislokationen . Detta är den beräknade tjockleken av en epitaxiell film, där filmen på grund av termodynamiska principer kommer att utveckla kristallografiska dislokationer för att minimera den elastiska energin som lagras i filmerna. Innan Lambert W applicerades för detta problem måste den kritiska tjockleken bestämmas genom att lösa en implicit ekvation. Lambert W förvandlar det till en explicit ekvation för analytisk hantering med lätthet.

Porösa medier

Lambert W -funktionen har använts inom området för vätskeflöde i porösa medier för att modellera lutningen av ett gränssnitt som separerar två gravitationsmässigt segregerade vätskor i en homogen lutad porös bädd med konstant dopp och tjocklek där den tyngre vätskan, injiceras i bottenänden, tränger undan tändvätskan som produceras i samma takt från den övre änden. Lösningens huvudgren motsvarar stabila förskjutningar medan −1-grenen gäller om förskjutningen är instabil med den tyngre vätskan som rinner under den lättare vätskan.

Bernoulli-tal och Todd-släkte

Ekvationen (kopplad med genereringsfunktionerna för Bernoulli-tal och Todd-släktet ):

$Y={\frac {X}{1-e^{X}}}$

kan lösas med hjälp av de två reella grenarna W ₀ och W ₋₁ :

$X(Y)={\begin{cases}W_{-1}\left(Ye^{Y}\right)-W_{ 0}\left(Ye^{Y}\right)=Y-W_{0}\left(Ye^{Y}\right)&{\text{för }}Y<-1,\\W_{0} \left(Ye^{Y}\right)-W_{-1}\left(Ye^{Y}\right)=Y-W_{-1}\left(Ye^{Y}\right)&{\ text{för }}-1<Y<0.\end{cases}}$

Denna applikation visar att grenskillnaden för W -funktionen kan användas för att lösa andra transcendentala ekvationer.

Statistik

Centroiden för en uppsättning histogram definierade med avseende på den symmetriserade Kullback–Leibler-divergensen (även kallad Jeffreys-divergensen) har en sluten form med Lambert W -funktionen.

Samling av tester för infektionssjukdomar

Att lösa den optimala gruppstorleken för att samla tester så att minst en individ är infekterad involverar Lambert W -funktionen.

Exakta lösningar av Schrödinger-ekvationen

Lambert W- funktionen uppträder i en kvantmekanisk potential, som ger den femte – bredvid de för den harmoniska oscillatorn plus centrifugal, Coulomb plus inverskvadrat, Morse och invers kvadratrotspotential – exakt lösning till den stationära en- dimensionell Schrödinger-ekvation i termer av de konfluenta hypergeometriska funktionerna. Potentialen ges som

$V={\frac {V_{0}}{1+W\left(e^{-{\frac {x}{\sigma }}}\right)}}.$

En egenhet med lösningen är att var och en av de två grundläggande lösningarna som utgör den allmänna lösningen av Schrödinger-ekvationen ges av en kombination av två sammanflytande hypergeometriska funktioner av ett argument proportionellt mot

$z=W\left(e^{-{\frac {x}{\sigma }}}\right).$

Lambert W -funktionen förekommer också i den exakta lösningen för den bundna tillståndsenergin för den endimensionella Schrödinger-ekvationen med en dubbel deltapotential .

Exakt lösning av QCD-kopplingskonstanten

I Quantum Chromodynamik , kvantfältteorin för Strong -interaktionen , beräknas kopplingskonstanten α s {\displaystyle \alpha _{\text{s}}} perturbatively, ordningen n motsvarar Feynman $inklusive$ n kvantloopar . Den första ordningen, n=1, lösningen är exakt (i den ordningen) och analytisk. Vid högre order, n>1, finns det ingen exakt och analytisk lösning och man använder vanligtvis en iterativ metod för att ge en ungefärlig lösning. Men för andra ordningen, n=2, ger Lambert-funktionen en exakt (om icke-analytisk) lösning.

Exakta lösningar av Einsteins vakuumekvationer

I Schwarzschilds metriska lösning av Einsteins vakuumekvationer behövs W -funktionen för att gå från Eddington–Finkelstein-koordinaterna till Schwarzschild-koordinaterna. Av denna anledning förekommer det också i konstruktionen av Kruskal-Szekeres-koordinaterna .

Resonanser för delta-skalpotentialen

Delta-skalpotentialens s-vågsresonanser kan skrivas exakt i termer av Lambert W -funktionen.

Termodynamisk jämvikt

Om en reaktion involverar reaktanter och produkter som har värmekapacitet som är konstant med temperaturen så lyder jämviktskonstanten K

$\ln K={\frac {a}{T}}+b+c\ln T$

för vissa konstanter a , b och c . När c (lika med Δ C _p / R ) inte är noll kan vi hitta värdet eller värdena på T där K är lika med ett givet värde enligt följande, där vi använder L för ln T .

${\begin{aligned}-a&=(b-\ln K)T+cT\ln T\\&=(b-\ln K)e^{L}+cLe^{L}\\[ 5pt]-{\frac {a}{c}}&=\left({\frac {b-\ln K}{c}}+L\right)e^{L}\\[5pt]-{\ frac {a}{c}}e^{\frac {b-\ln K}{c}}&=\left(L+{\frac {b-\ln K}{c}}\right)e^{ L+{\frac {b-\ln K}{c}}}\\[5pt]L&=W\left(-{\frac {a}{c}}e^{\frac {b-\ln K} {c}}\right)+{\frac {\ln Kb}{c}}\\[5pt]T&=\exp \left(W\left(-{\frac {a}{c}}e^{ \frac {b-\ln K}{c}}\right)+{\frac {\ln Kb}{c}}\right).\end{aligned}}$

Om a och c har samma tecken blir det antingen två lösningar eller ingen (eller en om argumentet för W är exakt − 1 / e ). (Den övre lösningen kanske inte är relevant.) Om de har motsatta tecken kommer det att finnas en lösning.

Fasseparation av polymerblandningar

Vid beräkningen av fasdiagrammet för termodynamiskt inkompatibla polymerblandningar enligt Edmond-Ogston-modellen formuleras lösningarna för binodala och bindelinjer i termer av Lambert W -funktioner.

Wiens förskjutningslag i ett D-dimensionellt universum

Wiens förskjutningslag uttrycks som $\nu _{\max }/T=\alpha =\mathrm {const}$ . Med $x=h\nu _{\max }/k_{\mathrm {B} }T$ och $d\ rho _{T}\left(x\right)/dx=0$ , där $\rho _{T}$ är den spektrala energitätheten, finner man $e^{-x}=1-{\frac {x}{ D}}$ . Lösningen $x=D+W\left(-De^{-D}\right)$ visar att den spektrala energitätheten är beroende av universums dimensionalitet .

AdS/CFT-korrespondens

De klassiska korrigeringarna av ändlig storlek av spridningsförhållandena för gigantiska magnoner, enkla spikar och GKP-strängar kan uttryckas i termer av Lambert W -funktionen.

Epidemiologi

I t → ∞ -gränsen för SIR-modellen har andelen mottagliga och återhämtade individer en lösning i termer av Lambert W -funktionen.

Fastställande av flygtiden för en projektil

Den totala tiden för färden för en projektil som upplever luftmotstånd proportionellt mot dess hastighet kan bestämmas i exakt form med hjälp av Lambert W -funktionen.

Elektromagnetisk ytvågsutbredning

Den transcendentala ekvationen som förekommer vid bestämningen av utbredningsvågantalet för en elektromagnetisk axiellt symmetrisk ytvåg (en enkel TM01-mode med låg dämpning) som utbreder sig i en cylindrisk metalltråd ger upphov till en ekvation som u ln u = v ( där u och v klumpar ihop de geometriska och fysiska faktorerna för problemet), vilket löses med Lambert W -funktionen. Den första lösningen på detta problem, på grund av Sommerfeld circa 1898, innehöll redan en iterativ metod för att bestämma värdet på Lambert W -funktionen.

Ortogonala banor av riktiga ellipser

Familjen av ellipser $x^{2}+(1-\varepsilon ^{2})y^{2}=\varepsilon ^{2}$ centrerad vid $(0,0)$ parametriseras av excentricitet $\varepsilon$ . De ortogonala banorna för denna familj ges av differentialekvationen $\left({\frac {1}{y}}+y\right)dy=\left({\frac {1}{x}}-x\right) dx$ vars allmänna lösning är familjen $y^{2}=$$W_{0}(x^{2}\ exp(-2C-x^{2}))$ .

Generaliseringar

Standard Lambert W -funktionen uttrycker exakta lösningar på transcendentala algebraiska ekvationer (i x ) av formen:

$$e^{-cx}=a_{0}(xr)$$

 

 

 

 

()

där a ₀ , c och r är reella konstanter. Lösningen är

$$x=r+{\frac {1}{c}}W\left({\frac {c\,e^{-cr}}{a_{0}}}\right).$$

Generaliseringar av Lambert W -funktionen inkluderar:

• En tillämpning på allmän relativitet och kvantmekanik ( kvantgravitation ) i lägre dimensioner, i själva verket en länk (okänd före 2007) mellan dessa två områden, där den högra sidan av ( 1 ) ersätts av ett kvadratiskt polynom i x :
  $$e^{-cx}=a_{0}\left(x-r_{1}\right)\left(x- r_{2}\höger),$$

   

   

   

   

  ()

  där r ₁ och r ₂ är reella distinkta konstanter, rötterna till det andragradspolynomet. Här är lösningen en funktion som har ett enda argument x men termer som r _i och a ₀ är parametrar för den funktionen. I detta avseende liknar generaliseringen den hypergeometriska funktionen och Meijer G -funktionen men den tillhör en annan klass av funktioner. När r ₁ = r ₂ , båda sidor av ( 2 ) kan faktoriseras och reduceras till ( 1 ) och därmed reduceras lösningen till den för standard W -funktionen. Ekvation ( 2 ) uttrycker ekvationen som styr dilatonfältet , från vilken härleds metriken för R = T eller linjärt tvåkroppsgravitationsproblem i 1 + 1 dimensioner (en rumsdimension och en tidsdimension) för fallet med ojämn vila massor, såväl som egenenergierna för den kvantmekaniska dubbelbrunns Dirac deltafunktionsmodellen för ojämlika laddningar i en dimension.

• Analytiska lösningar av egenenergierna i ett specialfall av det kvantmekaniska trekroppsproblemet , nämligen den (tredimensionella) vätemolekylen-jonen . Här ersätts den högra sidan av ( 1 ) av ett förhållande av oändlig ordningspolynom i x :
  $$e^{-cx}=a_{0}{\frac {\displaystyle \prod _{i=1}^{\infty }(x-r_{i})}{\displaystyle \prod _{i=1}^{\infty }(x-s_{i})}}$$

   

   

   

   

  ()

  där r _i och s _i är distinkta reella konstanter och x är en funktion av egenenergin och det interna kärnavståndet R . Ekvation ( 3 ) med dess specialiserade fall uttryckta i ( 1 ) och ( 2 ) är relaterad till en stor klass av fördröjningsdifferentialekvationer . GH Hardys begrepp om en "falsk derivata" ger exakta multipla rötter till specialfall av ( 3 ).

Tillämpningar av Lambert W -funktionen i grundläggande fysikaliska problem är inte uttömda ens för standardfallet uttryckt i ( 1 ) som nyligen sett inom området atom-, molekyl- och optisk fysik .

Tomter

• Plots av Lambert W -funktionen på det komplexa planet
• 

  ₀ z = Re( W ( x + iy ))

• 

  ₀ z = Im( W ( x + iy ))

• 

  z = | ₀ W ( x + iy ) |

• 

  Överlagring av de tre föregående tomterna

Numerisk utvärdering

W - funktionen kan approximeras med Newtons metod , med successiva approximationer till w = W ( z ) (så z = vi ^w ) är

$w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}+w_{j}e^ {w_{j}}}}.$

W - funktionen kan också approximeras med Halleys metod ,

$w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}\left(w_{j} +1\right)-{\dfrac {\left(w_{j}+2\right)\left(w_{j}e^{w_{j}}-z\right)}{2w_{j}+2 }}}}$

ges i Corless et al. att beräkna W .

För verklig ${\displaystyle x\geq -1/e} ,$ skulle den kunna approximeras med den kvadratiska rekursiva formeln för R. Iacono och JP Boyd:

$w_{n+1}(x)={\frac {w_{n}(x)}{1+w_{n}(x)}}\left(1+\log \left({\frac) {x}{w_{n}(x)}}\höger)\höger).$

Lajos Lóczi bevisar att genom att välja lämplig $w_{0}(x)$ ,

• om $x\in (e,\infty )$ : $w_{0} (x)=\log(x)-\log(\log(x)),$
• om $x\in (0,e):$$w_{0}(x)=x/e,$
• om $x\in (-1/e,0):$
  • för huvudgrenen $W_{0}$ : $w_{0}(x )={\frac {ex}{1+ex+{\sqrt {1+ex}}}}\log(1+{\sqrt {1+ex}}),$
  • för grenen $W_{-1}$ :
    • $w_{0}(x)=-1-{\sqrt {2(1+ex)}},$ för $x\in (-1/e,-1/4],$
    • $w_{0}(x)=\log(-x)-\log(-\log(- x)),$ för $x\in (-1/4,0),$

man kan bestämma det maximala antalet iterationssteg i förväg för vilken precision som helst:

• om $x\in (e,\infty )$ (sats 2.4): $0<W_{0}(x)-w_{n}(x)<\left(\log(1+1/e)\right)^{2^{n}},$
• om $x\in (0,e)$ (sats 2.9): ${ \displaystyle 0<W_{0}(x)-w_{n}(x)<{\frac {\left(1-1/e\right)^{2^{n}-1}}{5}} ,}$
• om $x\in (-1/e,0):$
  • för huvudgrenen $W_{0}$ (sats 2.17): $0<w_{n}(x) -W_{0}(x)<\left(1/10\right)^{2^{n}},$
  • för grenen $W_{-1}$ (sats 2.23): $0<W_{-1}(x)-w_{n}(x)<\left(1/2\right)^{2^{n}}.$

programvara

Lambert W -funktionen är implementerad som LambertW i Maple, lambertw i GP (och glambertW i PARI ), lambertw i Matlab , även lambertw i Octave med specfun -paketet, som lambert_w i Maxima, som ProductLog (med ett tyst alias LambertW ) i Mathematica , som lambertw i Python scipy s specialfunktionspaket, som LambertW i Perls nteorimodul , och som gsl_sf_lambert_W0 , fungerar gsl_sf_lambert_Wm1 i specialfunktionsdelen av GNU Scientific Library (GSL). I Boost C++-biblioteken är anropen lambert_w0 , lambert_wm1 , lambert_w0_prime och lambert_wm1_prime . I R är Lambert W -funktionen implementerad som lambertW0 och lambertWm1 fungerar i lamW- paketet.

C++-kod för alla grenar av den komplexa Lambert W -funktionen är tillgänglig på István Mezős hemsida.

Se även

• Wright Omega funktion
• Lamberts trinomialekvation
• Lagrange inversionssats
• Experimentell matematik
• Holstein–sillmetoden
• R = T -modell
• Ross π lemma

Anteckningar

•    Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996). "Om Lambert W -funktionen" (PDF) . Framsteg inom beräkningsmatematik . 5 : 329-359. arXiv : 1809.07369 . doi : 10.1007/BF02124750 . ISSN 1019-7168 . S2CID 29028411 . Arkiverad från originalet (PDF) 2010-12-14 . Hämtad 2007-03-10 .
• Chapeau-Blondeau, F.; Monir, A. (2002). "Utvärdering av Lambert W -funktionen och tillämpning på generering av generaliserat Gaussiskt brus med exponent 1/2" ( PDF) . IEEE Trans. Signalprocess . 50 (9). doi : 10.1109/TSP.2002.801912 . Arkiverad från originalet (PDF) 2012-03-28 . Hämtad 2004-03-10 .
•     Francis; et al. (2000). "Kvantitativ allmän teori för periodisk andning". Cirkulation . 102 (18): 2214–21. CiteSeerX 10.1.1.505.7194 . doi : 10.1161/01.cir.102.18.2214 . PMID 11056095 . S2CID 14410926 . (Lambert-funktionen används för att lösa fördröjningsdifferentiell dynamik i mänskliga sjukdomar.)
• Hayes, B. (2005). "Varför W ?" (PDF) . Amerikansk vetenskapsman . 93 (2): 104–108. doi : 10.1511/2005.2.104 . Arkiverad (PDF) från originalet 2022-10-10.
•    Roy, R.; Olver, FWJ (2010), "Lambert W function" , i Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (red.), NIST Handbook of Mathematical Functions , Cambridge University Press, ISBN 978-0-521-19225-5 , MR 2723248
•   Stewart, Seán M. (2005). "En ny elementär funktion för våra läroplaner?" (PDF) . Australian Senior Mathematics Journal . 19 (2): 8–26. ISSN 0819-4564 . Arkiverad (PDF) från originalet 2022-10-10.
• Veberic, D., "Ha kul med Lambert W ( x ) Function" arXiv:1003.1628 (2010) ;   Veberic, D. (2012). "Lambert W -funktion för tillämpningar inom fysik". Datorfysik kommunikation . 183 (12): 2622–2628. arXiv : 1209.0735 . Bibcode : 2012CoPhC.183.2622V . doi : 10.1016/j.cpc.2012.07.008 . S2CID 315088 .
•   Chatzigeorgiou, I. (2013). "Gränser för Lambert-funktionen och deras tillämpning på avbrottsanalys av användarsamarbete". IEEE kommunikationsbrev . 17 (8): 1505–1508. arXiv : 1601.04895 . doi : 10.1109/LCOMM.2013.070113.130972 . S2CID 10062685 .

externa länkar

• National Institute of Science and Technology Digital Library – Lambert W
• MathWorld – Lambert W -Funktion
• Beräknar Lambert W -funktionen
• Corless et al. Anteckningar om Lambert W forskning
• GPL C++ implementering med Halleys och Fritschs iteration.
• Specialfunktioner för GNU Scientific Library – GSL
• [3]