Termodynamikens andra lag

Termodynamikens andra lag är en fysisk lag baserad på universell erfarenhet av värme- och energiomvandlingar . Ett enkelt uttalande av lagen är att värme alltid rör sig från varmare föremål till kallare föremål (eller "nedför"), om inte energi i någon form tillförs för att vända värmeflödets riktning . En annan definition är: "Inte all värmeenergi kan omvandlas till arbete i en cyklisk process ."

Termodynamikens andra lag i andra versioner fastställer begreppet entropi som en fysisk egenskap hos ett termodynamiskt system . Det kan användas för att förutsäga huruvida processer är förbjudna trots att man följer kravet på bevarande av energi som uttrycks i termodynamikens första lag och tillhandahåller nödvändiga kriterier för spontana processer . Den andra lagen kan formuleras genom observationen att entropin i isolerade system som lämnas till spontan evolution inte kan minska, eftersom de alltid kommer till ett tillstånd av termodynamisk jämvikt där entropin är högst vid den givna inre energin. En ökning av den kombinerade entropin av system och omgivningar står för irreversibiliteten hos naturliga processer, ofta hänvisade till i begreppet tidens pil .

Historiskt sett var den andra lagen ett empiriskt fynd som accepterades som ett axiom för termodynamisk teori . Statistisk mekanik ger en mikroskopisk förklaring av lagen i termer av sannolikhetsfördelningar av tillstånden för stora sammansättningar av atomer eller molekyler . Den andra lagen har kommit till uttryck på många sätt. Dess första formulering, som föregick den korrekta definitionen av entropi och baserades på kaloriteori , är Carnots sats , formulerad av den franska vetenskapsmannen Sadi Carnot , som 1824 visade att effektiviteten av omvandling av värme till arbete i en värmemotor har en övre begränsa. Den första rigorösa definitionen av den andra lagen baserad på begreppet entropi kom från den tyske vetenskapsmannen Rudolf Clausius på 1850-talet och inkluderade hans uttalande att värme aldrig kan passera från en kallare till en varmare kropp utan att någon annan förändring, kopplad därmed, inträffar vid samma tid.

Termodynamikens andra lag tillåter definitionen av begreppet termodynamisk temperatur , som också förlitar sig på termodynamikens nollte lag .

Introduktion

Värme som strömmar från varmt vatten till kallt vatten

Termodynamikens första lag ger definitionen av den inre energin i ett termodynamiskt system och uttrycker dess förändring för ett slutet system i termer av arbete och värme . Det kan kopplas till lagen om energibevarande . Den andra lagen handlar om riktningen av naturliga processer. Den hävdar att en naturlig process bara pågår i en mening och inte är reversibel. Till exempel, när en väg för ledning eller strålning görs tillgänglig, strömmar värme alltid spontant från en varmare till en kallare kropp. Sådana fenomen redovisas i termer av entropiförändringar . Om ett isolerat system som innehåller distinkta delsystem initialt hålls i intern termodynamisk jämvikt genom inre uppdelning av ogenomträngliga väggar mellan delsystemen, och sedan någon operation gör väggarna mer permeabla, så utvecklas systemet spontant för att nå en slutlig ny intern termodynamisk jämvikt, och dess total entropi, $S$ , ökar.

I en reversibel eller kvasistatisk , idealiserad process för överföring av energi som värme till ett slutet termodynamiskt system av intresse, (som tillåter inträde eller utträde av energi – men inte överföring av materia), från ett termodynamiskt hjälpsystem, ett oändligt litet inkrement ( $\mathrm {d} S$ ) i entropin för systemet av intresse definieras som ett resultat av en oändlig överföring av värme ( $\delta Q$ ) till systemet av intresse, dividerat av den vanliga termodynamiska temperaturen $(T)$ för systemet av intresse och det termodynamiska hjälpsystemet:

$\mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,{\text{(slutet system; idealiserad, reversibel process)}}.$

Olika notationer används för en oändligt liten mängd värme $(\delta )$ och oändlig ändring av entropi $(\mathrm {d})$ eftersom entropi är en funktion av tillstånd , medan värme , liksom arbete, är det inte.

För en faktiskt möjlig infinitesimal process utan utbyte av massa med omgivningen kräver den andra lagen att ökningen i systementropin uppfyller ojämlikheten

$\mathrm {d} S>{\frac {\delta Q}{T_{\text{surr}}}}\,\,\,\,\,\,\,\,\,\,\ ,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(slutet system; faktiskt möjligt, oåterkallelig process).}}$

Detta beror på att en allmän process för detta fall (inget massutbyte mellan systemet och dess omgivning) kan innefatta arbete som utförs på systemet av dess omgivning, vilket kan ha friktions- eller viskösa effekter inuti systemet, eftersom en kemisk reaktion kan vara i framsteg, eller för att värmeöverföringen faktiskt bara sker irreversibelt, driven av en ändlig skillnad mellan systemtemperaturen ( T ) och temperaturen i omgivningen ( T _surr ).

Observera att likheten fortfarande gäller för rent värmeflöde (endast värmeflöde, ingen förändring i kemisk sammansättning och massa),

$\mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,{\text{(faktiskt möjlig kvasistatisk oåterkallelig process utan kompositionsändring).}}$

som ligger till grund för den exakta bestämningen av den absoluta entropin för rena ämnen från uppmätta värmekapacitetskurvor och entropiförändringar vid fasövergångar, dvs genom kalorimetri.

Genom att införa en uppsättning interna variabler $\xi$ för att beskriva avvikelsen för ett termodynamiskt system från ett kemiskt jämviktstillstånd i fysikalisk jämvikt (med det erforderliga väldefinierade enhetliga trycket P och temperaturen T ), kan man registrera likheten

$\mathrm {d} S={\frac {\delta Q}{T}}-{\frac {1}{T}}\summa _{j}\,\Xi _{j}\,\ delta \xi _{j}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ ,\,{\text{(slutet system; faktiskt möjlig kvasistatisk oåterkallelig process).}}$

Den andra termen representerar arbete av interna variabler som kan störas av yttre påverkan, men systemet kan inte utföra något positivt arbete via interna variabler. Detta uttalande introducerar omöjligheten av att vända det termodynamiska systemets evolution i tiden och kan betraktas som en formulering av termodynamikens andra princip – formuleringen, som naturligtvis är likvärdig med formuleringen av principen i termer av entropi .

Termodynamikens nollte lag tillåter i sitt vanliga korta uttalande att två kroppar i en termisk jämviktsrelation har samma temperatur, särskilt att en testkropp har samma temperatur som en termometrisk referenskropp. För en kropp i termisk jämvikt med en annan finns det oändligt många empiriska temperaturskalor, i allmänhet respektive beroende på egenskaperna hos en speciell termometrisk referenskropp. Den andra lagen tillåter en distingerad temperaturskala, som definierar en absolut, termodynamisk temperatur , oberoende av egenskaperna hos någon speciell termometrisk referenskropp.

Olika lagförklaringar

Termodynamikens andra lag kan uttryckas på många specifika sätt, de mest framträdande klassiska uttalandena är uttalandet av Rudolf Clausius (1854), uttalandet av Lord Kelvin (1851) och uttalandet i axiomatisk termodynamik av Constantin Carathéodory (1909). Dessa uttalanden gör lagen i allmänna fysiska termer med hänvisning till omöjligheten av vissa processer. Clausius och Kelvins uttalanden har visat sig vara likvärdiga.

Carnots princip

Det historiska ursprunget till termodynamikens andra lag var i Sadi Carnots teoretiska analys av värmeflödet i ångmaskiner (1824). Mittpunkten i den analysen, nu känd som en Carnot-motor , är en idealisk värmemotor som drivs i det begränsande läget av extrem långsamhet som kallas kvasistatisk, så att värme- och arbetsöverföringarna sker mellan delsystem som alltid är i sina egna inre tillstånd av termodynamisk jämvikt . Det representerar den teoretiska maximala verkningsgraden för en värmemotor som arbetar mellan två givna termiska eller värmereservoarer vid olika temperaturer. Carnots princip erkändes av Carnot vid en tidpunkt då kaloriteorin representerade den dominerande förståelsen av värmens natur, före erkännandet av termodynamikens första lag och före det matematiska uttrycket av begreppet entropi. Tolkad i ljuset av den första lagen är Carnots analys fysiskt likvärdig med termodynamikens andra lag och förblir giltig idag. Några exempel från hans bok är:

... varhelst det finns en temperaturskillnad kan drivkraft produceras.

Produktionen av drivkraft beror då i ångmaskiner inte på en faktisk förbrukning av kalorier, utan på dess transport från en varm kropp till en kall kropp ...

Värmens drivkraft är oberoende av de medel som används för att realisera den; dess kvantitet bestäms enbart av temperaturerna i kropparna mellan vilka sker, slutligen, överföringen av kalorier.

I moderna termer kan Carnots princip uttryckas mer exakt:

Effektiviteten för en kvasistatisk eller reversibel Carnot-cykel beror endast på temperaturen i de två värmebehållarna och är densamma, oavsett arbetsämne. En Carnot-motor som drivs på detta sätt är den mest effektiva möjliga värmemotorn med dessa två temperaturer.

Clausius uttalande

Den tyske vetenskapsmannen Rudolf Clausius lade grunden för termodynamikens andra lag 1850 genom att undersöka sambandet mellan värmeöverföring och arbete. Hans formulering av den andra lagen, som publicerades på tyska 1854, är känd som Clausius uttalande :

Värme kan aldrig övergå från en kallare till en varmare kropp utan att någon annan därmed sammanhängande förändring sker samtidigt.

Clausius uttalande använder begreppet "värmepassage". Som vanligt i termodynamiska diskussioner betyder detta "nettoöverföring av energi som värme", och syftar inte på bidragande överföringar åt det ena och det andra.

Värme kan inte spontant strömma från kalla regioner till varma regioner utan att externt arbete utförs på systemet, vilket framgår av t.ex. vanlig erfarenhet av kylning . I ett kylskåp överförs värme från kallt till varmt, men endast när det tvingas fram av en extern agent, kylsystemet.

Kelvin uttalanden

Lord Kelvin uttryckte den andra lagen i flera formuleringar.

Det är omöjligt för en självverkande maskin, utan hjälp av någon extern instans, att överföra värme från en kropp till en annan vid en högre temperatur.

Det är omöjligt, med hjälp av livlösa material, att härleda mekanisk effekt från någon del av materia genom att kyla den under temperaturen för det kallaste av de omgivande föremålen.

Likvärdighet mellan Clausius- och Kelvin-uttalandena

Härled Kelvin Statement från Clausius Statement

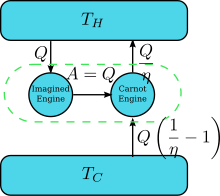
Anta att det finns en motor som bryter mot Kelvins uttalande: dvs en som tappar värme och omvandlar den helt till arbete (den dränerade värmen omvandlas helt till arbete) på ett cykliskt sätt utan något annat resultat. Para ihop den nu med en omvänd Carnot-motor som visas i den högra bilden. Verkningsgraden för en normal värmemotor är η och därför är verkningsgraden för den omvända värmemotorn 1/ η . Nettoeffekten och den enda effekten av det kombinerade motorparet är att överföra värme ${\textstyle \Delta Q=Q\left({\frac {1}{\eta }}-1\ höger)}$ från den kallare reservoaren till den varmare, vilket strider mot Clausius-påståendet. Detta är en konsekvens av termodynamikens första lag , att det totala systemets energi ska förbli densamma; ${\textstyle {\text{Input}}+{\text{Output}}=0\implies (Q+Q_{c})-{\frac { Q}{\eta }}=0}$ , så därför ${\textstyle Q_{c}=Q\left({\frac {1}{\eta }}-1\right )}$ , där (1) teckenkonventionen för värme används där värme som kommer in i (utgår från) en motor är positiv (negativ) och (2) ${\frac {Q}{\eta }}$ erhålls genom definitionen av motorns verkningsgrad när motorns drift inte är omvänd. En överträdelse av Kelvins uttalande innebär alltså en överträdelse av Clausius uttalandet, dvs. Clausius uttalandet innebär Kelvins uttalande. Vi kan bevisa på ett liknande sätt att Kelvin-påståendet innebär Clausius-påståendet, och därför är de två likvärdiga.

Plancks förslag

Planck erbjöd följande förslag som härrörde direkt från erfarenhet. Detta betraktas ibland som hans uttalande av den andra lagen, men han ansåg det som en utgångspunkt för härledningen av den andra lagen.

Det är omöjligt att konstruera en motor som fungerar i en hel cykel och som inte ger någon effekt förutom höjning av en vikt och kylning av en värmebehållare.

Samband mellan Kelvins uttalande och Plancks proposition

Det är nästan vanligt i läroböcker att tala om lagens "Kelvin–Planck-uttalande", som till exempel i texten av ter Haar och Wergeland . Denna version, även känd som värmemotorförklaringen , av den andra lagen säger att

Det är omöjligt att utforma en cykliskt fungerande anordning, vars enda effekt är att absorbera energi i form av värme från en enda termisk reservoar och att leverera en motsvarande mängd arbete .

Plancks uttalande

Planck angav den andra lagen enligt följande.

Varje process som sker i naturen fortskrider i den meningen att summan av entropierna för alla kroppar som deltar i processen ökar. I gränsen, dvs för reversibla processer, förblir summan av entropierna oförändrad.

Ganska likt Plancks uttalande är Uhlenbecks och Fords för irreversibla fenomen .

... i en irreversibel eller spontan förändring från ett jämviktstillstånd till ett annat (som till exempel temperaturutjämningen av två kroppar A och B, när de bringas i kontakt) ökar entropin alltid.

Principen för Carathéodory

Constantin Carathéodory formulerade termodynamik på en rent matematisk axiomatisk grund. Hans uttalande av den andra lagen är känd som principen om Carathéodory, som kan formuleras enligt följande:

I varje grannskap av något tillstånd S i ett adiabatiskt slutet system finns det tillstånd som är otillgängliga från S.

Med denna formulering beskrev han begreppet adiabatisk tillgänglighet för första gången och gav grunden för ett nytt delområde av klassisk termodynamik, ofta kallad geometrisk termodynamik . Det följer av Carathéodorys princip att den kvantitet energi som kvasistatiskt överförs som värme är en holonomisk processfunktion , med andra ord, $\delta Q=TdS$ .

Även om det nästan är brukligt i läroböcker att säga att Carathéodorys princip uttrycker den andra lagen och att behandla den som likvärdig med Clausius- eller Kelvin-Plancks uttalanden, så är det inte fallet. För att få allt innehåll i den andra lagen behöver Carathéodorys princip kompletteras med Plancks princip, att isokoriskt arbete alltid ökar den inre energin i ett slutet system som från början befann sig i sin egen inre termodynamiska jämvikt.

Plancks princip

1926 skrev Max Planck en viktig artikel om grunderna i termodynamiken. Han angav principen

Den inre energin i ett slutet system ökas genom en adiabatisk process, under vars varaktighet systemets volym förblir konstant.

Denna formulering nämner inte värme och nämner inte temperatur, inte ens entropi, och förlitar sig inte nödvändigtvis implicit på dessa begrepp, men den antyder innehållet i den andra lagen. Ett närbesläktat uttalande är att "friktionstryck aldrig fungerar positivt." Planck skrev: "Produktionen av värme genom friktion är irreversibel."

Utan att nämna entropi, denna princip av Planck anges i fysiska termer. Det är mycket nära besläktat med Kelvins uttalande precis ovan. Det är relevant att för ett system med konstant volym och moltal är entropin en monoton funktion av den inre energin. Ändå är denna princip av Planck faktiskt inte Plancks föredragna uttalande av den andra lagen, som citeras ovan, i ett tidigare underavsnitt av detta avsnitt av denna artikel, och förlitar sig på begreppet entropi.

Ett uttalande som i viss mening kompletterar Plancks princip görs av Borgnakke och Sonntag. De erbjuder det inte som ett fullständigt uttalande av den andra lagen:

... det finns bara ett sätt på vilket entropin i ett [slutet] system kan minskas, och det är att överföra värme från systemet.

Till skillnad från Plancks ovanstående princip, är denna uttryckligen i termer av entropiförändring. Borttagning av materia från ett system kan också minska dess entropi.

Påstående för ett system som har ett känt uttryck för sin inre energi som en funktion av dess omfattande tillståndsvariabler

Den andra lagen har visat sig vara ekvivalent med att den inre energin U är en svagt konvex funktion , när den skrivs som en funktion av omfattande egenskaper (massa, volym, entropi, ...).

Följderna

Evig rörelse av det andra slaget

Huvudartikel: Perpetual motion

Före upprättandet av den andra lagen hade många människor som var intresserade av att uppfinna en evighetsmaskin försökt kringgå begränsningarna i termodynamikens första lag genom att utvinna den massiva inre energin i miljön som maskinens kraft. En sådan maskin kallas en "perpetual motion machine of the second kind". Den andra lagen förklarade omöjligheten av sådana maskiner.

Carnots sats

Carnots teorem (1824) är en princip som begränsar den maximala verkningsgraden för alla möjliga motorer. Effektiviteten beror enbart på temperaturskillnaden mellan de varma och kalla termiska reservoarerna. Carnots sats säger:

• Alla irreversibla värmemotorer mellan två värmebehållare är mindre effektiva än en Carnot-motor som arbetar mellan samma behållare.
• Alla reversibla värmemotorer mellan två värmebehållare är lika effektiva med en Carnot-motor som arbetar mellan samma behållare.

I hans idealmodell kunde värmen från kalori omvandlat till arbete återställas genom att vända cykelns rörelse, ett koncept som senare kallas termodynamisk reversibilitet . Carnot postulerade dock vidare att en del kalorier går förlorade och inte omvandlas till mekaniskt arbete. Därför kunde ingen riktig värmemotor inse Carnot-cykelns reversibilitet och dömdes till att vara mindre effektiv.

Även om det formulerades i termer av kalorier (se den föråldrade kaloriteorin ), snarare än entropi , var detta en tidig insikt i den andra lagen.

Clausius ojämlikhet

Clausius -satsen (1854) säger att i en cyklisk process

$\oint {\frac {\delta Q}{T_{\text{surr}}}}\leq 0.$

Jämlikheten gäller i det reversibla fallet och den strikta olikheten gäller i det irreversibla fallet, med T _surr som temperaturen på värmebadet (omgivningen) här. Det reversibla fallet används för att introducera tillståndsfunktionen entropin . Detta beror på att i cykliska processer är variationen av en tillståndsfunktion noll från tillståndsfunktionalitet.

Termodynamisk temperatur

Huvudartikel: Termodynamisk temperatur

För en godtycklig värmemotor är verkningsgraden:

$\eta ={\frac {|W_{n}|}{q_{H}}}={\frac {q_{H}+q_{C}}{q_{H}}}=1-{ \frac {|q_{C}|}{|q_{H}|}}$

 

 

 

 

()

där W _n är det nettoarbete som utförs av motorn per cykel, q _H > 0 är den värme som tillförs motorn från en het reservoar, och q _C = - | q _C | < 0 är spillvärme som avges till en kall reservoar från motorn. Effektiviteten beror alltså endast på förhållandet | q _C | / | q _H |.

Carnots teorem säger att alla reversibla motorer som arbetar mellan samma värmereservoarer är lika effektiva. Således måste varje reversibel värmemotor som arbetar mellan temperaturerna TH och T _C ha samma verkningsgrad, det vill säga verkningsgraden är endast en funktion av temperaturer _:

${\frac {|q_{C}|}{|q_{H}|}}=f(T_{H},T_{C}).$

 

 

 

 

()

Dessutom måste en reversibel värmemotor som arbetar mellan temperaturerna T ₁ och T ₃ ha samma verkningsgrad som en som består av två cykler, en mellan T ₁ och en annan (mellanliggande) temperatur T ₂ , och den andra mellan T ₂ och T ₃ , där Ti _{_} > T2 _{_} > T3 _{_} . Detta beror på att om en del av tvåtaktsmotorn är dold så att den känns igen som en motor mellan reservoarerna vid temperaturerna T ₁ och T ₃ , då måste verkningsgraden för denna motor vara densamma som den andra motorn samtidigt reservoarer. Om vi ​​väljer motorer så att arbetet utfört av entaktsmotorn och tvåtaktsmotorn är samma, så skrivs verkningsgraden för varje värmemotor som nedan.

$\eta _{1}=1-{\frac {|q_{3}|}{|q_{1}|}}=1-f(T_{ 1},T_{3})$ ,

$\eta _{2}=1-{\frac {|q_{2}|}{|q_{1}|}}=1-f(T_{ 1},T_{2})$ ,

$\eta _{3}=1-{\frac {|q_{3}|}{|q_{2}|}}=1-f(T_{ 2},T_{3})$ .

_motorerna 2 och 3 gör tvåtaktsmotorn där det finns den mellanliggande reservoaren vid T2 . Vi har också använt det faktum att värmen $q_{2}$ passerar genom den mellanliggande termiska reservoaren vid $T_{2}$ utan att förlora sin energi. (Dvs $q_{2}$ går inte förlorad under sin passage genom reservoaren vid $T_{2}$ .) Detta faktum kan bevisas genom följande.

${\begin{aligned}&{{\eta }_{2}}=1-{\frac {|{{q}_{2}}|}{|{{q}_{1}} |}}\till |{{w}_{2}}|=|{{q}_{1}}|-|{{q}_{2}}|,\\&{{\eta }_ {3}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{2}}^{*}|}}\till |{{w}_{ 3}}|=|{{q}_{2}}^{*}|-|{{q}_{3}}|,\\&|{{w}_{2}}|+|{ {w}_{3}}|=(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}}^{* }|-|{{q}_{3}}|),\\&{{\eta }_{1}}=1-{\frac {|{{q}_{3}}|}{| {{q}_{1}}|}}={\frac {(|{{w}_{2}}|+|{{w}_{3}}|)}{|{{q}_ {1}}|}}={\frac {(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^ {*}|-|{{q}_{3}}|)}{|{{q}_{1}}|}}.\\\end{aligned}}$

För att få konsistensen i den sista ekvationen måste värmen $q_{2}$ som flygs från motorn 2 till mellanbehållaren vara lika med värmen $q_{2}^{ *}$ flög ut från behållaren till motorn 3.

Sedan

$f(T_{1},T_{3})={\frac {|q_{3}|}{|q_{1}|}}={\frac {|q_{2}||q_{ 3}|}{|q_{1}||q_{2}|}}=f(T_{1},T_{2})f(T_{2},T_{3}).$

Betrakta nu fallet där $T_{1}$ är en fast referenstemperatur: temperaturen för vattnets trippelpunkt är 273,16 Kelvin; $T_{1}=273,16 K$ . Sedan för alla T ₂ och T ₃ ,

$f(T_{2},T_{3})={\frac {f(T_{1},T_{3})}{f(T_{1},T_{2})}}={ \frac {273.16{\text{ K}}\cdot f(T_{1},T_{3})}{273.16{\text{ K}}\cdot f(T_{1},T_{2})} }.$

Därför, om termodynamisk temperatur T * definieras av

$T^{*}=273.16{\text{ K}}\cdot f(T_{1},T)$

då är funktionen f , sett som en funktion av termodynamiska temperaturer, helt enkelt

$f(T_{2},T_{3})=f(T_{2}^ {*},T_{3}^{*})={\frac {T_{3}^{*}}{T_{2}^{*}}},$

och referenstemperaturen T ₁ * = 273,16 K × f ( T ₁ , T ₁ ) = 273,16 K. (Varje referenstemperatur och vilket positivt numeriskt värde som helst kan användas – valet här motsvarar Kelvin- skalan.)

Entropi

Huvudartikel: Entropi (klassisk termodynamik)

Enligt Clausius jämlikhet , för en reversibel process

$\oint {\frac {\delta Q}{T}}=0$

Det betyder att linjeintegralen $\int _{L}{\frac {\delta Q}{T}}$ är vägoberoende för reversibla processer.

Så vi kan definiera en tillståndsfunktion S som kallas entropi, som för en reversibel process eller för ren värmeöverföring uppfyller

$dS={\frac {\delta Q}{T}}$

Med detta kan vi bara erhålla skillnaden i entropi genom att integrera ovanstående formel. För att erhålla det absoluta värdet behöver vi termodynamikens tredje lag , som säger att S = 0 vid absolut noll för perfekta kristaller.

För vilken irreversibel process som helst, eftersom entropi är en tillståndsfunktion, kan vi alltid koppla de initiala och terminala tillstånden med en imaginär reversibel process och integrera på den vägen för att beräkna skillnaden i entropi.

Vänd nu den reversibla processen och kombinera den med den nämnda irreversibla processen. Att tillämpa Clausius-ojämlikheten på denna slinga, med T _surr som temperaturen i omgivningen,

$-\Delta S+\int {\frac {\delta Q}{T_{surr}}}=\oint { \frac {\delta Q}{T_{surr}}}\leq 0$

Således,

$\Delta S\geq \int {\frac {\delta Q}{T_{surr}}}$

där jämlikheten gäller om omvandlingen är reversibel.

Lägg märke till att om processen är en adiabatisk process så är ${\displaystyle \delta Q=0} ,$ så $\Delta S\geq 0$ .

Energi, tillgängligt nyttigt arbete

Se även: Exergi

Ett viktigt och avslöjande idealiserat specialfall är att överväga att tillämpa den andra lagen på scenariot med ett isolerat system (kallat det totala systemet eller universum), som består av två delar: ett delsystem av intresse och delsystemets omgivning. Dessa omgivningar föreställs vara så stora att TR _de kan betraktas som en obegränsad värmereservoar vid temperatur och tryck PR – så att oavsett _hur mycket värme som överförs till (eller från) delsystemet, temperaturen på omgivningen kommer att förbli T _R ; och oavsett hur mycket volymen PR _av delsystemet expanderar (eller drar ihop sig), kommer trycket i omgivningen att förbli .

Vilka förändringar som än sker i dS och dS _R i delsystemets entropier och omgivningarna individuellt, får entropin S _tot för det isolerade totala systemet inte minska enligt termodynamikens andra lag:

$dS_{\mathrm {tot} }=dS+dS_{R}\geq 0$

Enligt termodynamikens första lag är förändringen dU i delsystemets inre energi summan av värmen δq som läggs till delsystemet, minus allt arbete δw som utförs av delsystemet, plus eventuell kemisk nettoenergi. gå in i delsystemet d Σ μ _iR N _i , så att:

$dU=\delta q-\delta w+d\left(\sum \mu _{iR}N_{i}\right)$

där μ _iR är de kemiska potentialerna för kemiska arter i den yttre omgivningen.

Nu är värmen som lämnar reservoaren och kommer in i delsystemet

${\displaystyle \delta q=T_{R}(-dS_{R})\leq T_{R}dS$

där vi först har använt definitionen av entropi i klassisk termodynamik (alternativt, inom statistisk termodynamik, kan sambandet mellan entropiförändring, temperatur och absorberad värme härledas); och sedan den andra lagen ojämlikhet från ovan.

Det följer därför att varje nätverk δw som utförs av delsystemet måste lyda

$\delta w\leq -dU+T_{R}dS+\sum \mu _{iR}dN_{i}$

Det är användbart att separera arbetet δw som utförs av delsystemet i det användbara arbetet δw _u som kan utföras av delsystemet, utöver det arbete p _R dV som utförs enbart genom att delsystemet expanderar mot det omgivande yttre trycket, ger följande relation för det användbara arbete (exergi) som kan utföras:

$\delta w_{u}\leq -d\left(U-T_{R}S+p_{ R}V-\sum \mu _{iR}N_{i}\right)$

Det är bekvämt att definiera den högra sidan som den exakta derivatan av en termodynamisk potential, kallad tillgängligheten eller exergin E för delsystemet,

$E=U-T_{R}S+p_{R}V-\sum \mu _{iR}N_{i}$

Den andra lagen innebär därför att för varje process som kan anses vara uppdelad helt enkelt i ett delsystem och en obegränsad temperatur- och tryckbehållare som den är i kontakt med,

$dE+\delta w_{u}\leq 0$

dvs förändringen i delsystemets exergi plus det nyttiga arbete som utförs av delsystemet (eller förändringen i delsystemets exergi minus eventuellt arbete, utöver det som görs av tryckbehållaren, som utförs på systemet) måste vara mindre än eller lika med noll .

Sammanfattningsvis, om ett korrekt oändligt reservoarliknande referenstillstånd väljs som systemomgivningen i den verkliga världen, då förutspår den andra lagen en minskning av E för en irreversibel process och ingen förändring för en reversibel process.

$dS_{tot}\geq 0$ är ekvivalent med $dE+\delta w_{u}\leq 0$

Detta uttryck tillsammans med det associerade referenstillståndet tillåter en konstruktör som arbetar i den makroskopiska skalan (över den termodynamiska gränsen ) att använda den andra lagen utan att direkt mäta eller beakta entropiförändringar i ett totalt isolerat system. ( Se även processingenjör ). Dessa förändringar har redan beaktats genom antagandet att det aktuella systemet kan nå jämvikt med referenstillståndet utan att ändra referenstillståndet. En effektivitet för en process eller samling av processer som jämför den med det reversibla idealet kan också hittas ( Se andra lagen effektivitet .)

Detta förhållningssätt till den andra lagen används i stor utsträckning inom ingenjörspraktik , miljöredovisning , systemekologi och andra discipliner.

Riktning av spontana processer

Den andra lagen bestämmer om en föreslagen fysisk eller kemisk process är förbjuden eller kan inträffa spontant. För isolerade system tillhandahålls ingen energi av omgivningen och den andra lagen kräver att endast systemets entropi måste öka: Δ S > 0. Exempel på spontana fysikaliska processer i isolerade system inkluderar följande:

• 1) Värme kan överföras från ett område med högre temperatur till en lägre temperatur (men inte tvärtom).
• 2) Mekanisk energi kan omvandlas till termisk energi (men inte tvärtom).
• 3) Ett löst ämne kan flytta från ett område med högre koncentration till ett område med lägre koncentration (men inte tvärtom).

Men för vissa icke-isolerade system som kan utbyta energi med sin omgivning, byter omgivningen tillräckligt med värme med systemet, eller gör tillräckligt med arbete på systemet, så att processerna sker i motsatt riktning. Detta är möjligt förutsatt att den totala entropiförändringen av systemet plus omgivningen är positiv enligt den andra lagen: Δ S _tot = Δ S + Δ S _R > 0. För de tre exemplen ovan:

• 1) Värme kan överföras från ett område med lägre temperatur till en högre temperatur i ett kylskåp eller i en värmepump . Dessa maskiner måste ge tillräckligt arbete till systemet.
• 2) Termisk energi kan omvandlas till mekaniskt arbete i en värmemotor , om tillräckligt med värme också avges till omgivningen.
• 3) Ett löst ämne kan flytta från ett område med lägre koncentration till ett område med högre koncentration i den biokemiska processen för aktiv transport , om tillräckligt arbete tillhandahålls av en koncentrationsgradient av en kemikalie som ATP eller av en elektrokemisk gradient .

Den andra lagen i kemisk termodynamik

För en spontan kemisk process i ett slutet system vid konstant temperatur och tryck utan icke- PV- arbete, omvandlas Clausius-olikheten Δ S > Q/T _surr till ett villkor för förändringen i Gibbs fria energi

$\Delta G<0$

eller d G < 0. För en liknande process vid konstant temperatur och volym måste förändringen i Helmholtz fria energi vara negativ, $\Delta A<0$ . Ett negativt värde på förändringen i fri energi ( G eller A ) är alltså en nödvändig förutsättning för att en process ska vara spontan. Detta är den mest användbara formen av termodynamikens andra lag inom kemi, där fri energiförändringar kan beräknas från tabulerade bildningsentalpier och standardmolära entropier av reaktanter och produkter. Det kemiska jämviktstillståndet vid konstant T och p utan elektriskt arbete är d G = 0.

Historia

Se även: Entropins historia

Nicolas Léonard Sadi Carnot i traditionell uniform av en student vid École Polytechnique

Den första teorin om omvandling av värme till mekaniskt arbete beror på Nicolas Léonard Sadi Carnot 1824. Han var den första som korrekt insåg att effektiviteten av denna omvandling beror på skillnaden i temperatur mellan en motor och dess omgivning.

Rudolf Clausius insåg betydelsen av James Prescott Joules arbete med bevarande av energi och var den förste som formulerade den andra lagen under 1850, i denna form: värme flödar inte spontant från kalla till varma kroppar. Även om det är allmänt känt nu, var detta i strid med den då populära kaloriteorin om värme, som ansåg värme som en vätska. Därifrån kunde han härleda principen om Sadi Carnot och definitionen av entropi (1865).

Etablerat under 1800-talet, säger Kelvin-Planck uttalande av den andra lagen, " Det är omöjligt för någon enhet som arbetar på en cykel att ta emot värme från en enda reservoar och producera en nettomängd arbete." Detta visades vara likvärdigt med Clausius uttalande.

Den ergodiska hypotesen är också viktig för Boltzmann -metoden. Den säger att över långa tidsperioder är tiden som spenderas i någon region av fasrummet för mikrotillstånd med samma energi proportionell mot volymen av denna region, dvs att alla tillgängliga mikrotillstånd är lika sannolika över en lång tidsperiod. På motsvarande sätt står det att tidsgenomsnitt och medelvärde över den statistiska ensemblen är samma.

Det finns en traditionell doktrin, som börjar med Clausius, att entropi kan förstås i termer av molekylär "störning" inom ett makroskopiskt system . Denna doktrin är föråldrad.

Redovisning av Clausius

Rudolf Clausius

År 1865 uttalade den tyske fysikern Rudolf Clausius vad han kallade den "andra grundläggande satsen i den mekaniska värmeteorin " i följande form:

$\int {\frac {\delta Q}{T}}=-N$

där Q är värme, T är temperatur och N är "ekvivalensvärdet" för alla okompenserade transformationer involverade i en cyklisk process. Senare, 1865, skulle Clausius komma att definiera "ekvivalensvärde" som entropi. I hälarna på denna definition, samma år, lästes den mest kända versionen av den andra lagen i en presentation på Philosophical Society of Zurich den 24 april, där Clausius, i slutet av sin presentation, avslutar:

Universums entropi tenderar till ett maximum.

Detta uttalande är den mest kända formuleringen av den andra lagen. På grund av lösheten i dess språk, t.ex. universum , såväl som avsaknaden av specifika förhållanden, t.ex. öppna, stängda eller isolerade, tar många människor detta enkla påstående som att termodynamikens andra lag gäller praktiskt taget alla tänkbara ämnen. Det är inte sant; detta uttalande är bara en förenklad version av en mer utökad och exakt beskrivning.

När det gäller tidsvariation är det matematiska uttalandet i den andra lagen för ett isolerat system som genomgår en godtycklig transformation:

${\frac {dS}{dt}}\geq 0$

var

S är systemets entropi och

t är tiden .

Likhetstecknet gäller efter utjämning. Ett alternativt sätt att formulera den andra lagen för isolerade system är:

${\frac {dS}{dt}}={\dot {S}}_{i}$ med ${\dot {S}}_ {i}\geq 0$

med ${\dot {S}}_{i}$ summan av hastigheten för entropiproduktion av alla processer i systemet. Fördelen med denna formulering är att den visar effekten av entropiproduktionen. Entropiproduktionshastigheten är ett mycket viktigt begrepp eftersom det bestämmer (begränsar) effektiviteten hos termiska maskiner. Multiplicerat med omgivningstemperaturen $T_{a}$ ger det den så kallade förbrukade energin $P_{diss}=T_{a}{\dot {S }}_{i}$ .

Uttrycket för den andra lagen för slutna system (så att tillåta värmeväxling och flytta gränser, men inte utbyte av materia) är:

${\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}_{ i}$ med ${\dot {S}}_{i}\geq 0$

Här

${\dot {Q}}$ är värmeflödet in i systemet

$T$ är temperaturen vid den punkt där värmen kommer in i systemet.

Jämlikhetstecknet gäller i det fall att endast reversibla processer äger rum inne i systemet. Om irreversibla processer äger rum (vilket är fallet i verkliga system i drift) gäller >-tecknet. Om värme tillförs systemet på flera ställen måste vi ta den algebraiska summan av motsvarande termer.

För öppna system (som även tillåter utbyte av materia):

${\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S} }+{\dot {S}}_{i}$ med ${\dot {S}}_{i}\geq 0$

Här är ${\dot {S}}$ flödet av entropi in i systemet associerat med flödet av materia som kommer in i systemet. Det ska inte förväxlas med tidsderivatan av entropin. Om materia tillförs på flera ställen måste vi ta den algebraiska summan av dessa bidrag.

Statistisk mekanik

Statistisk mekanik ger en förklaring till den andra lagen genom att postulera att ett material är sammansatt av atomer och molekyler som är i konstant rörelse. En speciell uppsättning positioner och hastigheter för varje partikel i systemet kallas ett mikrotillstånd i systemet och på grund av den konstanta rörelsen ändrar systemet hela tiden sitt mikrotillstånd. Statistisk mekanik postulerar att varje mikrotillstånd som systemet kan befinna sig i är lika sannolikt att inträffa i jämvikt, och när detta antagande görs leder det direkt till slutsatsen att den andra lagen måste gälla i statistisk mening. Det vill säga, den andra lagen kommer att hålla i genomsnitt, med en statistisk variation i storleksordningen 1/ √ N där N är antalet partiklar i systemet. För vardagliga (makroskopiska) situationer är sannolikheten att den andra lagen kommer att överträdas praktiskt taget noll. Men för system med ett litet antal partiklar kan termodynamiska parametrar, inklusive entropin, visa signifikanta statistiska avvikelser från det som förutsägs av den andra lagen. Klassisk termodynamisk teori behandlar inte dessa statistiska variationer.

Härledning från statistisk mekanik

Ytterligare information: H-sats

Det första mekaniska argumentet i den kinetiska teorin om gaser att molekylära kollisioner innebär en utjämning av temperaturer och därmed en tendens till jämvikt berodde på James Clerk Maxwell 1860; Ludwig Boltzmann med sin H-sats från 1872 hävdade också att på grund av kollisioner borde gaser över tiden tendera mot Maxwell-Boltzmann-fördelningen .

På grund av Loschmidts paradox måste härledningar av den andra lagen göra ett antagande om det förflutna, nämligen att systemet är okorrelerat någon gång i det förflutna; detta möjliggör enkel probabilistisk behandling. Detta antagande är vanligtvis tänkt som ett gränsvillkor , och därmed är den andra lagen i slutändan en konsekvens av de initiala förhållandena någonstans i det förflutna, förmodligen i början av universum (Big Bang ), även om andra scenarier också har föreslagits.

Givet dessa antaganden, inom statistisk mekanik, är den andra lagen inte ett postulat, utan snarare en konsekvens av det fundamentala postulatet , även känt som det lika föregående sannolikhetspostulatet, så länge man är tydlig med att enkla sannolikhetsargument endast tillämpas på framtid, medan det för det förflutna finns ytterligare informationskällor som berättar att det var låg entropi. Den första delen av den andra lagen, som säger att entropin i ett termiskt isolerat system bara kan öka, är en trivial konsekvens av postulatet för lika föregående sannolikhet, om vi begränsar begreppet entropi till system i termisk jämvikt . Entropin för ett isolerat system i termisk jämvikt som innehåller en energimängd $E$ är:

$S=k_{\mathrm {B} }\ln \left[\Omega \left(E\right)\right]$

där $\Omega \left(E\right)$ är antalet kvanttillstånd i ett litet intervall mellan $E$ och $E+\delta E$ . Här $\delta E$ ett makroskopiskt litet energiintervall som hålls fast. Strängt taget betyder detta att entropin beror på valet av $\delta E$ . I den termodynamiska gränsen (dvs. i gränsen för oändligt stor systemstorlek), beror den specifika entropin (entropin per volymenhet eller per massenhet) inte av $\delta E$ .

Antag att vi har ett isolerat system vars makroskopiska tillstånd specificeras av ett antal variabler. Dessa makroskopiska variabler kan t.ex. referera till den totala volymen, kolvarnas positioner i systemet etc. Då $\Omega$ att bero på värdena för dessa variabler. Om en variabel inte är fixerad (t.ex. klämmer vi inte en kolv i ett visst läge), då eftersom alla tillgängliga tillstånd är lika sannolika i jämvikt, kommer den fria variabeln i jämvikt att vara sådan att Ω {\displaystyle \ $}$ är maximerad vid den givna energin i det isolerade systemet eftersom det är den mest sannolika situationen i jämvikt.

Om variabeln initialt var fixerad till något värde sedan vid frisläppandet och när den nya jämvikten har uppnåtts, det faktum att variabeln kommer att justera sig själv så att $\Omega$ maximeras, innebär att entropin kommer att ha ökat eller kommer att har förblivit detsamma (om värdet som variabeln fixerades till råkade vara jämviktsvärdet). Anta att vi utgår från en jämviktssituation och att vi plötsligt tar bort en begränsning för en variabel. Sedan direkt efter att vi gjort detta finns det ett antal $\Omega$ tillgängliga mikrotillstånd, men jämvikten har ännu inte uppnåtts, så de faktiska sannolikheterna för att systemet är i något tillgängligt tillstånd är ännu inte lika med den tidigare sannolikheten av $1/\Omega$ . Vi har redan sett att i det slutliga jämviktstillståndet kommer entropin att ha ökat eller förblivit densamma i förhållande till det tidigare jämviktstillståndet. Boltzmanns H-sats bevisar dock att kvantiteten H ökar monotont som funktion av tiden under det mellanliggande tillståndet utanför jämvikt.

Härledning av entropiförändringen för reversibla processer

Den andra delen av den andra lagen säger att entropiförändringen av ett system som genomgår en reversibel process ges av:

$dS={\frac {\delta Q}{T}}$

där temperaturen definieras som:

${\frac {1}{k_{\mathrm {B} }T}}\equiv \beta \equiv {\frac {d \ln \left[\Omega \left(E\right)\right]}{dE}}$

Se här för motiveringen till denna definition. Antag att systemet har någon extern parameter, x , som kan ändras. I allmänhet kommer systemets energiegentillstånd att bero på x . Enligt adiabatiska sats , inom gränsen för en oändligt långsam förändring av systemets Hamiltonian, kommer systemet att stanna i samma energiegentillstånd och därmed ändra sin energi i enlighet med energiförändringen i energiegentillståndet det befinner sig i.

Den generaliserade kraften, $Xdx$ , som motsvarar den externa variabeln x definieras så att är det arbete som utförs av systemet om x ökas med ett belopp dx . Till exempel, om x är volymen så är X trycket. Den generaliserade kraften för ett system som är känt för att vara i energiegentillstånd $E_{r}$ ges av:

$X=-{\frac {dE_{r}}{dx}}$

Eftersom systemet kan vara i vilket energiegentillstånd som helst inom intervallet $\delta E$ , definierar vi den generaliserade kraften för systemet som förväntningsvärdet för uttrycket ovan:

$X=-\left\langle {\frac {dE_{r}}{dx}}\right\rangle \,$

För att utvärdera medelvärdet partitionerar vi $\Omega \left(E\right)$ energiegentillstånden genom att räkna hur många av dem som har ett värde för ${\frac {dE_ {r}}{dx}}$ inom ett intervall mellan $Y$ och $Y+\delta Y$ . Genom att ringa detta nummer ${\displaystyle \Omega _{Y}\left(E\right)} ,$ har vi:

$\Omega \left(E\right)=\summa _{Y}\Omega _{Y}\left(E\right)\,$

Genomsnittet som definierar den generaliserade kraften kan nu skrivas:

$X=-{\frac {1}{\Omega \left(E\right)}}\summa _{Y}Y\Omega _ {Y}\left(E\right)\,$

Vi kan relatera detta till derivatan av entropin med avseende på x vid konstant energi E enligt följande. Antag att vi ändrar x till x + dx . Då $\Omega \left(E\right)$ att ändras eftersom energiegentillstånden beror på x , vilket gör att energiegentillstånd flyttas in i eller utanför intervallet mellan $E$ och $E+\delta E$ . Låt oss återigen fokusera på energiegentillstånden för vilka ${\textstyle {\frac {dE_{r}}{dx}}}$ ligger inom intervallet mellan $Y$ och $Y+\delta Y$ . Eftersom dessa energiegentillstånd ökar i energi med Ydx , flyttas alla sådana energiegentillstånd som ligger i intervallet från E – Ydx till E från under E till över E. Det finns

$N_{Y}\left(E\right)={\frac {\Omega _{Y}\left(E\right)}{ \delta E}}Ydx\,$

sådana energiegentillstånd. Om $Ydx\leq \delta E$ , kommer alla dessa energiegentillstånd att flytta in i området mellan $E$ och $E+\delta E$ och bidra till en ökning av $\Omega$ . Antalet energiegentillstånd som rör sig från under $E+\delta E$ till över $E+\delta E$ ges av $N_ {Y}\left(E+\delta E\right)$ . Skillnaden

$N_{Y}\left(E\right)-N_{Y}\left(E+\delta E\right)\,$

är alltså nettobidraget till ökningen av $\Omega$ . Observera att om Y dx är större än $\delta E$ kommer det att finnas energiegentillstånd som rör sig från under E till ovanför $E+\delta E$ . De räknas i både $N_{Y}\left(E\right)$ och $N_{Y}\left(E+\delta E\right )$ , därför är uttrycket ovan också giltigt i det fallet.

Att uttrycka ovanstående uttryck som en derivata med avseende på E och summera över Y ger uttrycket:

$\left({\frac {\partial \Omega }{\partial x }}\right)_{E}=-\summa _{Y}Y\left({\frac {\partial \Omega _{Y}}{\partial E}}\right)_{x}=\left ({\frac {\partial \left(\Omega X\right)}{\partial E}}\right)_{x}\,$

Den logaritmiska derivatan av $\Omega$ med avseende på x ges alltså av:

$\left({\frac {\partial \ln \left(\Omega \right)}{\partial x} }\right)_{E}=\beta X+\left({\frac {\partial X}{\partial E}}\right)_{x}\,$

Den första termen är intensiv, dvs den skalas inte med systemstorlek. Däremot skalar den sista termen som den omvända systemstorleken och kommer därmed att försvinna i den termodynamiska gränsen. Vi har alltså funnit att:

$\left({\frac {\partial S}{\partial x}}\right)_{E}={\frac {X}{T}}\,$

Att kombinera detta med

$\left({\frac {\partial S}{\partial E}}\right)_{x}={\frac {1}{T}}\,$

ger:

$dS=\left({\frac {\partial S }{\partial E}}\right)_{x}dE+\left({\frac {\partial S}{\partial x}}\right)_{E}dx={\frac {dE}{T} }+{\frac {X}{T}}dx={\frac {\delta Q}{T}}\,$

Härledning för system som beskrivs av den kanoniska ensemblen

Om ett system är i termisk kontakt med ett värmebad vid någon temperatur T då, i jämvikt, ges sannolikhetsfördelningen över energiegenvärdena av den kanoniska ensemblen :

$P_{j}={\frac {\exp \left(-{\frac {E_{j}}{k_{\mathrm {B} } T}}\höger)}{Z}}$

Här är Z en faktor som normaliserar summan av alla sannolikheter till 1, denna funktion är känd som partitionsfunktionen . Vi betraktar nu en oändligt liten reversibel förändring i temperaturen och i de yttre parametrar som energinivåerna beror på. Det följer av den allmänna formeln för entropin:

$S=-k_{\mathrm {B} }\sum _{j}P_{j}\ln \left(P_{j}\right )$

den där

$dS=-k_{\mathrm {B} }\summa _{j}\ln \left(P_{j}\right)dP_ {j}$

Att infoga formeln för $P_{j}$ för den kanoniska ensemblen här ger:

$dS= {\frac {1}{T}}\summa _{j}E_{j}dP_{j}={\frac {1}{T}}\summa _{j}d\left(E_{j}P_ {j}\right)-{\frac {1}{T}}\sum _{j}P_{j}dE_{j}={\frac {dE+\delta W}{T}}={\frac { \delta Q}{T}}$

Initiala förhållanden vid Big Bang

Som utvecklats ovan, tros det att termodynamikens andra lag är ett resultat av de initiala förhållandena med mycket låg entropi vid Big Bang . Ur statistisk synpunkt var det mycket speciella förhållanden. Å andra sidan var de ganska enkla, eftersom universum - eller åtminstone den del av det som det observerbara universum utvecklats från - verkar ha varit extremt enhetligt.

Detta kan verka något paradoxalt, eftersom enhetliga förhållanden (t.ex. blandade snarare än separerade gaser) i många fysiska system har hög entropi. Paradoxen är löst när man inser att gravitationssystem har negativ värmekapacitet , så att när gravitationen är viktig har enhetliga förhållanden (t.ex. gas med enhetlig densitet) faktiskt lägre entropi jämfört med olikformiga (t.ex. svarta hål i tomt utrymme). Ytterligare ett tillvägagångssätt är att universum hade hög (eller till och med maximal) entropi givet dess storlek, men när universum växte kom det snabbt ur termodynamisk jämvikt, dess entropi ökade endast något jämfört med ökningen av maximal möjlig entropi, och därför har den kom fram till en mycket låg entropi jämfört med det mycket större möjliga maximum givet dess senare storlek.

När det gäller anledningen till att initiala förhållanden var sådana, är ett förslag att kosmologisk inflation var tillräckligt för att utplåna icke-jämnhet, medan en annan är att universum skapades spontant där skapelsemekanismen antyder lågentropi initiala förhållanden.

Levande organismer

Det finns två principiella sätt att formulera termodynamik, (a) genom passager från ett tillstånd av termodynamisk jämvikt till ett annat, och (b) genom cykliska processer, genom vilka systemet lämnas oförändrat, samtidigt som den totala entropin i omgivningen ökar. Dessa två sätt hjälper till att förstå livets processer. Levande organismers termodynamik har övervägts av många författare, såsom Erwin Schrödinger , Léon Brillouin och Isaac Asimov .

Till en rättvis uppskattning kan levande organismer betraktas som exempel på (b). Ungefär, ett djurs fysiska tillstånd cyklar för varje dag, vilket lämnar djuret nästan oförändrat. Djur tar i sig mat, vatten och syre, och som ett resultat av ämnesomsättningen ger de ut nedbrytningsprodukter och värme. Växter tar in strålningsenergi från solen, som kan ses som värme, och koldioxid och vatten. De ger ut syre. På så sätt växer de. Så småningom dör de, och deras kvarlevor ruttnar bort och förvandlas till största delen tillbaka till koldioxid och vatten. Detta kan ses som en cyklisk process. Sammantaget kommer solljuset från en högtemperaturkälla, solen, och dess energi leds till en lägre temperatursänka, dvs strålas ut i rymden. Detta är en ökning av entropin i växtens omgivning. Således följer djur och växter termodynamikens andra lag, betraktad i termer av cykliska processer.

Vidare står levande organismers förmåga att växa och öka i komplexitet, samt att bilda korrelationer med sin omgivning i form av anpassning och minne, inte i motsats till den andra lagen – snarare liknar den allmänna resultat som följer av den. : Enligt vissa definitioner resulterar en ökning av entropin också i en ökning av komplexiteten, och för ett ändligt system som interagerar med ändliga reservoarer är en ökning av entropin ekvivalent med en ökning av korrelationerna mellan systemet och reservoarerna.

Levande organismer kan betraktas som öppna system, eftersom materia passerar in och ut från dem. Termodynamik hos öppna system betraktas för närvarande ofta i termer av passager från ett tillstånd av termodynamisk jämvikt till ett annat, eller i termer av flöden i approximationen av lokal termodynamisk jämvikt. Problemet för levande organismer kan ytterligare förenklas genom approximationen att anta ett stabilt tillstånd med oföränderliga flöden. Allmänna principer för entropiproduktion för sådana approximationer är föremål för en orolig aktuell debatt eller forskning .

Gravitationssystem

Vanligtvis har system för vilka gravitationen inte är viktig en positiv värmekapacitet , vilket innebär att deras temperatur stiger med deras inre energi. Därför, när energi strömmar från ett högtemperaturobjekt till ett lågtemperaturobjekt, sjunker källtemperaturen medan diskbänkstemperaturen höjs; temperaturskillnader tenderar därför att minska med tiden.

Detta är inte alltid fallet för system där gravitationskraften är viktig: system som är bundna av sin egen gravitation, som stjärnor, kan ha negativ värmekapacitet. När de drar ihop sig minskar både deras totala energi och entropi men deras inre temperatur kan öka . Detta kan ha betydelse för protostjärnor och till och med gasjätteplaneter som Jupiter . När entropin för den svartkroppsstrålning som emitteras av kropparna är inkluderad, kan systemets totala entropi dock visas öka även när planetens eller stjärnans entropi minskar.

Eftersom gravitationen är den viktigaste kraften som verkar på kosmologiska skalor, kan det vara svårt eller omöjligt att tillämpa den andra lagen på universum som helhet.

Icke-jämviktstillstånd

Huvudartikel: Non-equilibrium thermodynamics

Teorin om klassisk eller jämviktstermodynamik är idealiserad. Ett huvudpostulat eller antagande, ofta inte ens uttryckligen, är förekomsten av system i sina egna interna tillstånd av termodynamisk jämvikt. I allmänhet är ett område av rymden som innehåller ett fysiskt system vid en given tidpunkt, som kan finnas i naturen, inte i termodynamisk jämvikt, läs på de mest stringenta termer. I lösare termer, ingenting i hela universum är eller har någonsin varit i exakt termodynamisk jämvikt.

För fysisk analys är det ofta tillräckligt bekvämt att göra ett antagande om termodynamisk jämvikt . Ett sådant antagande kan förlita sig på försök och misstag för att motivera det. Om antagandet är motiverat kan det ofta vara mycket värdefullt och användbart eftersom det gör teorin om termodynamiken tillgänglig. Element i jämviktsantagandet är att ett system observeras vara oföränderligt under en obestämd lång tid, och att det finns så många partiklar i ett system att dess partikelformiga natur kan ignoreras helt. Under ett sådant jämviktsantagande finns det i allmänhet inga makroskopiskt detekterbara fluktuationer . Det finns ett undantag, fallet med kritiska tillstånd , som för blotta ögat uppvisar fenomenet kritisk opalescens . För laboratoriestudier av kritiska tillstånd behövs exceptionellt långa observationstider.

I alla fall innebär antagandet om termodynamisk jämvikt, när det väl har gjorts, som en konsekvens att ingen förmodad kandidat "fluktuation" förändrar systemets entropi.

Det kan lätt hända att ett fysiskt system uppvisar interna makroskopiska förändringar som är tillräckligt snabba för att ogiltigförklara antagandet om entropins beständighet. Eller att ett fysiskt system har så få partiklar att den partikelformiga naturen visar sig i observerbara fluktuationer. Då ska antagandet om termodynamisk jämvikt överges. Det finns ingen okvalificerad allmän definition av entropi för icke-jämviktstillstånd.

Det finns mellanliggande fall, där antagandet om lokal termodynamisk jämvikt är en mycket bra approximation, men strängt taget är det fortfarande en approximation, inte teoretiskt ideal.

För icke-jämviktssituationer i allmänhet kan det vara användbart att överväga statistiska mekaniska definitioner av andra kvantiteter som bekvämt kan kallas 'entropi', men de bör inte förväxlas eller sammanblandas med termodynamisk entropi korrekt definierad för den andra lagen. Dessa andra storheter tillhör verkligen den statistiska mekaniken, inte till termodynamiken, den andra lagens primära område.

Fysiken för makroskopiskt observerbara fluktuationer ligger utanför ramen för denna artikel.

Tidens pil

Se även: Tidens pil och Entropi (tidens pil)

Termodynamikens andra lag är en fysisk lag som inte är symmetrisk mot omkastning av tidsriktningen. Detta strider inte mot symmetrier som observeras i fysikens grundläggande lagar (särskilt CPT-symmetri ) eftersom den andra lagen gäller statistiskt på tidsasymmetriska randvillkor. Den andra lagen har varit relaterad till skillnaden mellan att röra sig framåt och bakåt i tiden, eller till principen att orsak föregår effekt ( tidens orsakspil eller kausalitet ).

Oåterkallelighet

Irreversibilitet i termodynamiska processer är en konsekvens av den asymmetriska karaktären hos termodynamiska operationer, och inte av några inre irreversibla mikroskopiska egenskaper hos kropparna. Termodynamiska operationer är makroskopiska externa ingrepp som påtvingas de deltagande organen, inte härledda från deras inre egenskaper. Det finns välrenommerade "paradoxer" som uppstår när man inte inser detta.

Loschmidts paradox

Huvudartikel: Loschmidts paradox

Loschmidts paradox , även känd som reversibilitetsparadoxen, är invändningen att det inte ska vara möjligt att härleda en irreversibel process från den tidssymmetriska dynamik som beskriver den mikroskopiska utvecklingen av ett makroskopiskt system.

Enligt Schrödinger , "Det är nu ganska uppenbart på vilket sätt du måste omformulera entropilagen – eller för den delen, alla andra irreversibla uttalanden – så att de kan härledas från reversibla modeller. Du får inte tala av ett isolerat system men åtminstone av två, som du för tillfället kan betrakta som isolerade från resten av världen, men inte alltid från varandra." De två systemen är isolerade från varandra av väggen, tills den avlägsnas genom den termodynamiska operationen, som föreskrivs i lagen. Den termodynamiska driften är externt pålagd, inte föremål för de reversibla mikroskopiska dynamiska lagarna som styr systemens beståndsdelar. Det är orsaken till irreversibiliteten. Lagförklaringen i denna artikel överensstämmer med Schrödingers råd. Orsak-verkan-relationen ligger logiskt före den andra lagen, inte härledd från den.

Poincarés återfallsteorem

Huvudartikel: Poincarés återfallsteorem

Poincarés återfallsteoremet betraktar en teoretisk mikroskopisk beskrivning av ett isolerat fysiskt system. Detta kan betraktas som en modell av ett termodynamiskt system efter att en termodynamisk operation har tagit bort en innervägg. Systemet kommer efter tillräckligt lång tid att återgå till ett mikroskopiskt definierat tillstånd mycket nära det initiala. Poincarés återkomsttid är den tid som förflutit fram till återkomsten. Den är oerhört lång, troligen längre än universums liv, och beror känsligt på geometrin hos väggen som togs bort av den termodynamiska operationen. Återkommandesatsen kan uppfattas som uppenbarligen motsägelsefull termodynamikens andra lag. Mer uppenbart är det dock helt enkelt en mikroskopisk modell av termodynamisk jämvikt i ett isolerat system som bildas genom att en vägg avlägsnas mellan två system. För ett typiskt termodynamiskt system är upprepningstiden så stor (många många gånger längre än universums livstid) att man för alla praktiska ändamål inte kan observera upprepningen. Man skulle ändå kunna tänka sig att man kunde vänta på att Poincaré återkommer och sedan sätta in väggen som togs bort av den termodynamiska operationen igen. Det är då uppenbart att uppkomsten av irreversibilitet beror på den fullständiga oförutsägbarheten av Poincaré-upprepningen endast med tanke på att det initiala tillståndet var ett av termodynamisk jämvikt, vilket är fallet i makroskopisk termodynamik. Även om man kunde vänta på det, har man ingen praktisk möjlighet att välja rätt ögonblick för att sätta in väggen igen. Poincarés återfallssats ger en lösning på Loschmidts paradox. Om ett isolerat termodynamiskt system kunde övervakas över allt fler multiplar av den genomsnittliga Poincaré-återfallstiden, skulle systemets termodynamiska beteende bli invariant under tidsomkastning.

James Clerk Maxwell

Maxwells demon

Huvudartikel: Maxwells demon

James Clerk Maxwell föreställde sig en behållare uppdelad i två delar, A och B . Båda delarna är fyllda med samma gas vid lika temperaturer och placerade bredvid varandra, åtskilda av en vägg. En imaginär demon som observerar molekylerna på båda sidor vaktar en mikroskopisk falllucka i väggen. När en snabbare än genomsnittet molekyl från A flyger mot falluckan, öppnar demonen den och molekylen kommer att flyga från A till B. Medelhastigheten för molekylerna i B kommer att ha ökat medan de i A kommer att ha avtagit i genomsnitt. Eftersom medelmolekylär hastighet motsvarar temperaturen, minskar temperaturen i A och ökar i B , i motsats till termodynamikens andra lag.

Ett svar på denna fråga föreslogs 1929 av Leó Szilárd och senare av Léon Brillouin . Szilárd påpekade att en verklig Maxwells demon skulle behöva ha något sätt att mäta molekylär hastighet, och att handlingen att skaffa information skulle kräva en energiförbrukning.

Maxwells "demon" ändrar upprepade gånger väggens permeabilitet mellan A och B . Den utför därför termodynamiska operationer i mikroskopisk skala, inte bara att observera vanliga spontana eller naturliga makroskopiska termodynamiska processer.

Citat

Lagen att entropin alltid ökar har, tror jag, den högsta positionen bland naturlagarna . Om någon påpekar för dig att din husdjursteori om universum inte håller med Maxwells ekvationer – så mycket värre för Maxwells ekvationer. Om det visar sig motsägas av observation – ja, dessa experimentalister klurar på saker ibland. Men om din teori visar sig vara emot termodynamikens andra lag kan jag inte ge dig något hopp; det finns inget annat än att kollapsa i djupaste förnedring.

— Sir Arthur Stanley Eddington , The Nature of the Physical World (1927)

Det har varit nästan lika många formuleringar av den andra lagen som det har varit diskussioner om den.

— Filosof/fysiker PW Bridgman , (1941)

Clausius är författaren till det sibylliska yttrandet, "Universums energi är konstant; universums entropi tenderar till ett maximum." Målen för kontinuumtermomekaniken slutar långt ifrån att förklara "universum", men inom den teorin kan vi lätt härleda ett explicit uttalande på vissa sätt som påminner om Clausius, men som bara hänvisar till ett blygsamt objekt: en isolerad kropp av ändlig storlek.

-   Truesdell, C. , Muncaster, RG (1980). Fundamentals of Maxwells Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics , Academic Press, New York, ISBN 0-12-701350-4 , sid. 17.

Se även

• Termodynamikens nolllag
• Termodynamikens första lag
• Termodynamikens tredje lag
• Ojämlikhet mellan Clausius och Duhem
• Fluktuationssats
• Universums värmedöd
• Termodynamikens historia
• Jarzynski jämställdhet
• Termodynamikens lagar
• Maximal entropi termodynamik
• Kvanttermodynamik
• Reflektioner över eldens drivkraft
• Relativistisk värmeledning
• Termisk diod
• Termodynamisk jämvikt

Källor

•    Adkins, CJ (1983). Jämviktstermodynamik (1:a uppl. 1968, 3:e uppl.). Cambridge Storbritannien: Cambridge University Press. ISBN 0-521-25445-0 . OCLC 9132054 .
•   Atkins, PW , de Paula, J. (2006). Atkins' Physical Chemistry , åttonde upplagan, WH Freeman, New York, ISBN 978-0-7167-8759-4 .
•   Attard, P. (2012). Non-equilibrium Thermodynamics and Statistical Mechanics: Foundations and Applications , Oxford University Press, Oxford UK, ISBN 978-0-19-966276-0 .
•   Baierlein, R. (1999). Thermal Physics , Cambridge University Press, Cambridge UK, ISBN 0-521-59082-5 .
•   Bailyn, M. (1994). A Survey of Thermodynamics , American Institute of Physics, New York, ISBN 0-88318-797-3 .
•    Blundell, Stephen J. ; Blundell, Katherine M. (2010). Begrepp i termisk fysik (2:a uppl.). Oxford: Oxford University Press . doi : 10.1093/acprof:oso/9780199562091.001.0001 . ISBN 9780199562107 . OCLC 607907330 .
• Boltzmann, L. (1896/1964). Föreläsningar om gasteori , översatt av SG Brush, University of California Press, Berkeley.
•   Borgnakke, C., Sonntag., RE (2009). Fundamentals of Thermodynamics , sjunde upplagan, Wiley, ISBN 978-0-470-04192-5 .
• Buchdahl, HA (1966). The Concepts of Classical Thermodynamics , Cambridge University Press, Cambridge UK.
• Bridgman, PW (1943). The Nature of Thermodynamics , Harvard University Press, Cambridge MA.
•   Callen, HB (1960/1985). Thermodynamics and an Introduction to Thermostatistics , (1:a upplagan 1960) 2:a upplagan 1985, Wiley, New York, ISBN 0-471-86256-8 .
•   C. Carathéodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik" . Matematiska Annalen . 67 (3): 355–386. doi : 10.1007/bf01450409 . S2CID 118230148 . Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können. (s.363) . En översättning kan hittas här . Även en mestadels tillförlitlig översättning finns hos Kestin, J. (1976). The Second Law of Thermodynamics , Dowden, Hutchinson & Ross, Stroudsburg PA.
•   Carnot, S. (1824/1986). Reflections on the motive power of fire , Manchester University Press, Manchester UK, ISBN 0-7190-1741-6 . Också här.
• Chapman, S. , Cowling, TG (1939/1970). Den matematiska teorin om olikformiga gaser. An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases , tredje upplagan 1970, Cambridge University Press, London.
• Clausius, R. (1850). "Ueber Die Bewegende Kraft Der Wärme Und Die Gesetze, Welche Sich Daraus Für Die Wärmelehre Selbst Ableiten Lassen" . Annalen der Physik . 79 (4): 368–397, 500–524. Bibcode : 1850AnP...155..500C . doi : 10.1002/andp.18501550403 . hdl : 2027/uc1.$b242250 . Hämtad 26 juni 2012 . Översatt till engelska: Clausius, R. (juli 1851). "Om värmens rörliga kraft och lagarna om själva värmens natur som kan härledas därifrån" . London, Edinburgh och Dublin Philosophical Magazine och Journal of Science . 4:a. 2 (VIII): 1–21, 102–119. doi : 10.1080/14786445108646819 . Hämtad 26 juni 2012 .
• Clausius, R. (1854). "Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie" (PDF) . Annalen der Physik . xciii (12): 481–506. Bibcode : 1854AnP...169..481C . doi : 10.1002/andp.18541691202 . Hämtad 24 mars 2014 . Översatt till engelska: Clausius, R. (juli 1856). "På en modifierad form av den andra grundläggande satsen i den mekaniska värmeteorin" . London, Edinburgh och Dublin Philosophical Magazine och Journal of Science . 4:a. 2:86 . _ Hämtad 24 mars 2014 . Omtryckt i: Clausius, R. (1867). Den mekaniska teorin om värme – med dess tillämpningar på ångmaskinen och på kroppars fysiska egenskaper . London: John van Voorst . Hämtad 19 juni 2012 . utgåvor:PwR_Sbkwa8IC.
•   Denbigh, K. (1954/1981). Principerna för kemisk jämvikt. With Applications in Chemistry and Chemical Engineering , fjärde upplagan, Cambridge University Press, Cambridge UK, ISBN 0-521-23682-7 .
•   Eu, BC (2002). Generaliserad termodynamik. Thermodynamics of Irreversible Processes and Generalized Hydrodynamics , Kluwer Academic Publishers, Dordrecht, ISBN 1-4020-0788-4 .
• Gibbs, JW (1876/1878). Om jämvikten mellan heterogena ämnen, Trans. Conn. Acad. , 3 : 108–248, 343–524, omtryckt i The Collected Works of J. Willard Gibbs, Ph.D, LL. D. , redigerad av WR Longley, RG Van Name, Longmans, Green & Co., New York, 1928, volym 1, s. 55–353.
•   Griem, HR (2005). Principles of Plasma Spectroscopy (Cambridge Monographs on Plasma Physics) , Cambridge University Press, New York ISBN 0-521-61941-6 .
•   Glansdorff, P., Prigogine, I. (1971). Termodynamisk teori om struktur, stabilitet och fluktuationer , Wiley-Interscience, London, 1971, ISBN 0-471-30280-5 .
•    Grandy, Walter T. (2008). Entropi och makroskopiska systems tidsutveckling . Oxford New York: Oxford University Press. ISBN 978-0-19-954617-6 . OCLC 190843367 .
•   Greven, A., Keller, G., Warnecke (redaktörer) (2003). Entropy , Princeton University Press, Princeton NJ, ISBN 0-691-11338-6 .
• Guggenheim, EA (1949). 'Statistical basis of thermodynamics', Research , 2 : 450–454.
• Guggenheim, EA (1967). Termodynamik. An Advanced Treatment for Chemists and Physicists , femte reviderade upplagan, North Holland, Amsterdam.
• Gyarmati, I. (1967/1970) Non-equilibrium Thermodynamics. Fältteori och variationsprinciper , översatt av E. Gyarmati och WF Heinz, Springer, New York.
•   Kittel, C. , Kroemer, H. (1969/1980). Thermal Physics , andra upplagan, Freeman, San Francisco, CA, ISBN 0-7167-1088-9 .
•   Kondepudi, D., Prigogine, I. (1998). Modern Thermodynamics: From Heat Engines to Dissipative Structures , John Wiley & Sons, Chichester, ISBN 0-471-97393-9 .
•   Lebon, G., Jou, D., Casas-Vázquez, J. (2008). Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers , Springer-Verlag, Berlin, ISBN 978-3-540-74252-4 .
•   Lieb, EH; Yngvason, J. (1999). "Fysiken och matematiken i termodynamikens andra lag". Fysiska rapporter . 310 (1): 1–96. arXiv : cond-mat/9708200 . Bibcode : 1999PhR...310...1L . doi : 10.1016/S0370-1573(98)00082-9 . S2CID 119620408 .
• Lieb, EH, Yngvason, J. (2003). The Entropy of Classical Thermodynamics, s. 147–195, kapitel 8 i Entropy , Greven, A., Keller, G., Warnecke (redaktörer) (2003).
•   Mandl, F. (1988). Statistisk fysik (andra upplagan). Wiley & Sons . ISBN 978-0-471-91533-1 .
•   Maxwell, JC (1867). "Om den dynamiska teorin om gaser". Phil. Trans. R. Soc. Lond . 157 : 49–88. doi : 10.1098/rstl.1867.0004 . S2CID 96568430 .
•   Müller, I. (1985). Thermodynamics , Pitman, London, ISBN 0-273-08577-8 .
• Müller, I. (2003). Entropy in Nonequilibrium, s. 79–109, kapitel 5 av Entropy , Greven, A., Keller, G., Warnecke (redaktörer) (2003).
•   Münster, A. (1970), Classical Thermodynamics , översatt av ES Halberstadt, Wiley–Interscience, London, ISBN 0-471-62430-6 .
• Pippard, AB (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics , originalpublikation 1957, nytryck 1966, Cambridge University Press, Cambridge UK.
• Planck, M. (1897/1903). Treatise on Thermodynamics , översatt av A. Ogg, Longmans Green, London, sid. 100.
• Planck. M. (1914). The Theory of Heat Radiation , en översättning av Masius, M. av den andra tyska upplagan, P. Blakistons Son & Co., Philadelphia.
• Planck, M. (1926). Über die Begründung des zweiten Hauptsatzes der Thermodynamik, Sitzungsberichte der Preussischen Akademie der Wissenschaften: Physikalisch-mathematische Klasse : 453–463.
• Pokrovskii VN (2005) Utökad termodynamik i ett diskret system, Eur. J. Phys. vol. 26, 769-781.
• Pokrovskii, Vladimir N. (2013). "En härledning av de huvudsakliga relationerna mellan termodynamiken i icke-jämvikt" . ISRN Termodynamik . 2013 : 1–9. doi : 10.1155/2013/906136 .
•   Quinn, TJ (1983). Temperatur , Academic Press, London, ISBN 0-12-569680-9 .
•   Rao, YVC (2004). En introduktion till termodynamik . Universitetspressen. sid. 213. ISBN 978-81-7371-461-0 .
• Roberts, JK, Miller, AR (1928/1960). Heat and Thermodynamics , (första upplagan 1928), femte upplagan, Blackie & Son Limited, Glasgow.
• Schrödinger, E. (1950). Irreversibilitet, Proc. R. Ir. Acad. , A53 : 189-195.
• ter Haar, D. , Wergeland, H. (1966). Elements of Thermodynamics , Addison-Wesley Publishing, Reading MA.
• Thomson, W. (1851). "Om den dynamiska teorin om värme, med numeriska resultat härledda från Mr Joules motsvarighet till en termisk enhet, och M. Regnaults observationer om ånga" . Transaktioner från Royal Society of Edinburgh . XX (del II): 261–268, 289–298. Även publicerad i Thomson, W. (december 1852). "Om den dynamiska teorin om värme, med numeriska resultat härledda från Mr Joules motsvarighet till en termisk enhet, och M. Regnaults observationer om ånga" . Philos. Mag . 4. IV (22): 13 . Hämtad 25 juni 2012 .
• Thomson, W. (1852). Om naturens universella tendens att försvinna mekanisk energi Philosophical Magazine, Ser. 4, sid. 304.
• Tisza, L. (1966). Generalized Thermodynamics , MIT Press, Cambridge MA.
•   Truesdell, C. (1980). The Tragicomical History of Thermodynamics 1822–1854 , Springer, New York, ISBN 0-387-90403-4 .
• Uffink, J. (2001). Bluffa dig i termodynamikens andra lag, Stud. Hist. Phil. Mod. Phys. , 32 (3): 305-394.
•   Uffink, J. (2003). Irreversibility and the Second Law of Thermodynamics, kapitel 7 i Entropy , Greven, A., Keller, G., Warnecke (redaktörer) (2003), Princeton University Press, Princeton NJ, ISBN 0-691-11338-6 .
• Uhlenbeck, GE , Ford, GW (1963). Föreläsningar i statistisk mekanik , American Mathematical Society, Providence RI.
• Zemansky, MW (1968). Värme och termodynamik. An Intermediate Textbook , femte upplagan, McGraw-Hill Book Company, New York.

Vidare läsning

•   Goldstein, Martin och Inge F., 1993. Kylskåpet och universum . Harvard Univ. Tryck. Kap. 4–9 innehåller en introduktion till den andra lagen, en lite mindre teknisk än denna post. ISBN 978-0-674-75324-2
•   Leff, Harvey S. och Rex, Andrew F. (red.) 2003. Maxwell's Demon 2: Entropi, klassisk och kvantinformation, beräkningar . Bristol Storbritannien; Philadelphia PA: Institute of Physics . ISBN 978-0-585-49237-7
•   Halliwell, JJ (1994). Fysiskt ursprung av tidsasymmetri . Cambridge. ISBN 978-0-521-56837-1 . (teknisk).
• Carnot, Sadi (1890). Thurston, Robert Henry (red.). Reflektioner om värmens drivkraft och om maskiner som är anpassade för att utveckla den kraften . New York: J. Wiley & Sons. ( fulltext av 1897 ed. ) ( html Arkiverad 2007-08-18 på Wayback Machine )
•   Stephen Jay Kline (1999). The Low-Down on Entropy and Interpretive Thermodynamics , La Cañada, CA: DCW Industries. ISBN 1-928729-01-0 .
•    Kostic, M (2011). Återbesök den andra lagen om energinedbrytning och generering av entropi: från Sadi Carnots geniala resonemang till holistisk generalisering . AIP Conf. Proc . AIP Conference Proceedings. Vol. 1411. s. 327–350. Bibcode : 2011AIPC.1411..327K . CiteSeerX 10.1.1.405.1945 . doi : 10.1063/1.3665247 . ISBN 978-0-7354-0985-9 . även vid [1] .

externa länkar

• Stanford Encyclopedia of Philosophy : " Philosophy of Statistical Mechanics " – av Lawrence Sklar.
• Termodynamikens andra lag i MIT-kursen Unified Thermodynamics and Propulsion från Prof. ZS Spakovszky
• ET Jaynes , 1988, " The evolution of Carnot's princip ," i GJ Erickson och CR Smith (red.) Maximum-Entropy and Bayesian Methods in Science and Engineering, Vol. 1: sid. 267.
• Caratheodory, C., "Undersökning av termodynamikens grunder," övers. av DH Delphenich
• The Second Law of Thermodynamics , BBC Radio 4-diskussion med John Gribbin, Peter Atkins och Monica Grady ( In Our Time , 16 december 2004)
• "The Second Law Mystique" , ​​Alexey Nikulov och Daniel Sheehan, Entropy , 2004
• Journal of the International Society for the History of Philosophy of Science, 2012