Naturliga tal objekt

I kategoriteorin är ett objekt med naturliga tal ( NNO ) ett objekt som har en rekursiv struktur som liknar naturliga tal . Mer exakt, i en kategori E med ett terminalobjekt 1, ges ett NNO N av:

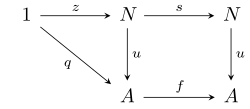
1. ett globalt element z : 1 → N , och
2. en pil s : N → N ,

så att för alla objekt A av E , globalt element q : 1 → A , och pil f : A → A , det finns en unik pil u : N → A så att:

1. u ∘ z = q , och
2. u ∘ s = f ∘ u .

Med andra ord, triangeln och kvadraten i följande diagram pendlar.

Paret ( q , f ) kallas ibland rekursionsdata för u , givet i form av en rekursiv definition :

1. ⊢ u ( z ) = q
2. y ∈ _E N ⊢ u ( s y ) = f ( u ( y ))

Ovanstående definition är den universella egenskapen hos NNO, vilket betyder att de definieras upp till kanonisk isomorfism . Om pilen u enligt definitionen ovan bara måste existera, det vill säga unikhet krävs inte, så kallas N en svag NNO.

Motsvarande definitioner

NNO i kartesiska slutna kategorier (CCC) eller topoi definieras ibland på följande ekvivalenta sätt (på grund av Lawvere ): för varje par av pilar g : A → B och f : B → B , finns det ett unikt h : N × A → B så att kvadraterna i följande diagram pendlar.

Samma konstruktion definierar svaga NNO i kartesiska kategorier som inte är kartesiska stängda.

I en kategori med ett terminalobjekt 1 och binära samprodukter (betecknade med +), kan en NNO definieras som den initiala algebra för endofunktorn som verkar på objekt med X ↦ 1 + X och på pilar med f ↦ id ₁ + f .

Egenskaper

• Varje NNO är ett initialobjekt i kategorin diagram av formen

$1{\xrightarrow {~\quad q\quad ~}}A{\xrightarrow {~\quad f\quad ~ }}A$

• Om en kartesisk sluten kategori har svaga NNO, så har varje del av den också en svag NNO.
• NNO:er kan användas för icke-standardiserade modeller av typteori på ett sätt som är analogt med icke-standardiserade analysmodeller. Sådana kategorier (eller topoi) tenderar att ha "oändligt många" icke-standardiserade naturliga tal. (Som alltid finns det enkla sätt att få icke-standardiserade NNO:er; till exempel om z = sz , i vilket fall kategorin eller topos E är trivial.)
• Freyd visade att z och s bildar ett samproduktdiagram för NNO; också, ! _N : N → 1 är en utjämnare av s och 1 _N , dvs varje par av globala element i N är sammankopplade med hjälp av s ; dessutom kännetecknar detta par fakta alla NNO:er.

Exempel

• I Set , kategorin för mängder , är de naturliga standardtalen ett NNO. Ett terminalobjekt i Set är en singleton , och en funktion ur en singleton plockar ut ett enda element i en mängd. De naturliga talen 𝐍 är ett NNO där z är en funktion från en singelton till 𝐍 vars bild är noll, och s är efterföljande funktion . (Vi kunde faktiskt tillåta z att välja ut vilken som helst element av 𝐍, och den resulterande NNO skulle vara isomorf till denna.) Man kan bevisa att diagrammet i definitionen pendlar med matematisk induktion .
• I kategorin typer av Martin-Löfs typteori (med typer som objekt och funktioner som pilar) är den normala naturliga taltypen nat en NNO. Man kan använda recursorn för nat för att visa att lämpligt diagram pendlar.
• Antag att ${\mathcal {E}}$ är en Grothendieck-topos med terminalobjekt $\top$ och att ${\mathcal {E}} \simeq \mathbf {Shv} ({\mathfrak {C}},J)$ för viss Grothendieck-topologi $J$ i kategorin ${\mathfrak {C}}$ . Sedan om $\Gamma _{\mathbb {N} }$ är den konstanta förstaven på ${\displaystyle {\mathfrak {C}}} , då$ är NNO i ${\mathcal {E}}$ sköljning av $\Gamma _{\mathbb {N} }$ och kan visas i formen
  $$\mathbb {N} _{\mathcal {E}}\cong \left(\Gamma _{\mathbb {N} }\right)^{++}\cong \coprod _{n\in \mathbb {N} }\top .$$

Se även

• Peanos axiom för aritmetiken
• Kategorisk logik

•    Johnstone, Peter T. (2002). Sketcher of an Elephant: a Topos Theory Compendium . Oxford: Oxford University Press. ISBN 0198534256 . OCLC 50164783 .
• Lawvere, William (2005) [1964]. "En elementär teori om kategorin uppsättningar (lång version) med kommentarer" . Omtryck i teori och tillämpningar av kategorier . 11 : 1–35.

externa länkar

• Föreläsningsanteckningar från Robert Harper som diskuterar NNO:er i avsnitt 2.2: https://www.cs.cmu.edu/~rwh/courses/hott/notes/notes_week3.pdf
• Ett blogginlägg av Clive Newstead på n -Category Cafe: https://golem.ph.utexas.edu/category/2014/01/an_elementary_theory_of_the_ca.html
• Anteckningar om datatyper som algebror för endofunctors av datavetaren Philip Wadler : http://homepages.inf.ed.ac.uk/wadler/papers/free-rectypes/free-rectypes.txt
• Anteckningar om nLab : https://ncatlab.org/nlab/show/ETCS