Harmonisk fyrhörning
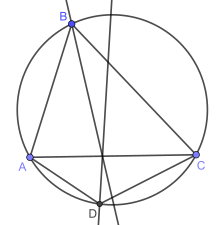
Inom euklidisk geometri är en harmonisk fyrhörning , eller harmonisk fyrhörning , en fyrhörning som kan skrivas in i en cirkel ( cyklisk fyrhörning ) där produkterna av längderna på motsatta sidor är lika. Den har flera viktiga egenskaper.
Egenskaper
Låt ABCD vara en harmonisk fyrhörning och M mittpunkten av diagonalen AC . Sedan:
- Tangenter till den omskrivna cirkeln vid punkterna A och C och den räta linjen BD antingen skär varandra i en punkt eller är inbördes parallella .
- Vinklarna ∠BMC och ∠DMC är lika.
- Vinklarnas bisektrar vid B och D skär varandra på diagonalen AC .
- En diagonal BD av fyrhörningen är en symmedian av vinklarna vid B och D i trianglarna ∆ ABC och ∆ ADC .
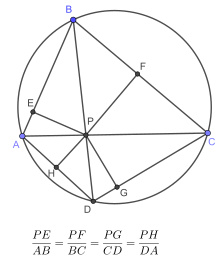
- Skärningspunkten för diagonalerna är belägen mot sidorna av fyrhörningen till proportionella avstånd till längden på dessa sidor.
Vidare läsning
- Gallatly, W. "Den harmoniska fyrhörningen." §124 i The Modern Geometry of the Triangle, 2nd ed. London: Hodgson, s. 90 och 92, 1913.
Kategorier: