Tangentiell fyrhörning

En tangentiell fyrhörning med sin incirkel

I euklidisk geometri är en tangentiell fyrhörning (ibland bara tangent fyrhörning ) eller omskriven fyrhörning en konvex fyrhörning vars sidor alla kan tangera en singelcirkel inom fyrhörningen. Denna cirkel kallas incirkeln av fyrhörningen eller dess inskrivna cirkel, dess centrum är incenter och dess radie kallas inradius . Eftersom dessa fyrhörningar kan ritas kring eller avgränsa deras incirklar, har de också kallats omskrivbara fyrhörningar , omskrivbara fyrhörningar och omskrivbara fyrhörningar . Tangentiala fyrhörningar är ett specialfall av tangentiella polygoner .

Andra mindre frekvent använda namn för denna klass av fyrhörningar är inskriptbar fyrhörning , inskrivbar fyrhörning , inskrivbar fyrhörning , cirkumcyklisk fyrhörning och samcyklisk fyrhörning . På grund av risken för förväxling med en fyrhörning som har en omsluten cirkel, som kallas en cyklisk fyrhörning eller inskriven fyrhörning, är det att föredra att inte använda något av de fem sista namnen.

Alla trianglar kan ha en incirkel, men inte alla fyrhörningar har det. Ett exempel på en fyrhörning som inte kan vara tangentiell är en rektangel som inte är kvadratisk . Avsnittskarakteriseringarna nedan anger vilka nödvändiga och tillräckliga villkor en fyrhörning måste uppfylla för att kunna ha en incirkel.

Speciella fall

Exempel på tangentiella fyrhörningar är drakarna , som inkluderar romberna , som i sin tur inkluderar kvadraterna . Drakarna är exakt de tangentiella fyrhörningarna som också är ortodiagonala . En högerdrake är en drake med en omsluten cirkel . Om en fyrhörning är både tangentiell och cyklisk kallas den för en bicentrisk fyrhörning , och om den är både tangentiell och en trapets , kallas den tangentiell trapets .

Karakteriseringar

I en tangentiell fyrhörning möts de fyra vinkelhalveringslinjerna i mitten av incirkeln. Omvänt måste en konvex fyrhörning där de fyra vinkelhalveringslinjerna möts i en punkt vara tangentiell och den gemensamma punkten är mitten.

Enligt Pitotsatsen summerar de två paren av motsatta sidor i en tangentiell fyrhörning till samma totala längd, vilket är lika med halvperimetern s av fyrhörningen:

$a+c=b+d={\frac {a+b+c+d}{2}}=s.$

Omvänt en konvex fyrhörning där a + c = b + d måste vara tangentiell.

Om motsatta sidor i en konvex fyrhörning ABCD (som inte är en trapets ) skär varandra vid E och F , så är den tangentiell om och endast om någon av

$\displaystyle BE+BF=DE+DF$

eller

$\displaystyle AE-EC=AF-FC:$

nödvändigt och tillräckligt villkor är att en konvex fyrhörning ABCD är tangentiell om och endast om cirklarna i de två trianglarna ABC och ADC tangerar varandra.

En karakterisering av vinklarna som bildas av diagonal BD och de fyra sidorna av en fyrhörning ABCD beror på Iosifescu. Han bevisade 1954 att en konvex fyrhörning har en incirkel om och bara om

$\tan {\frac {\angle ABD}{2}}\cdot \tan {\frac {\angle BDC}{2}}=\tan {\frac {\angle ADB}{2}}\cdot \tan {\frac {\angle DBC}{2}}.$

En tangentiell fyrhörning (i blått) med sin incirkel (streckad linje) och de fyra yttre tangentcirklarna (i rött), var och en tangent till en given sida och förlängningarna av de intilliggande sidorna.

Vidare är en konvex fyrhörning med på varandra följande sidor a , b , c , d tangentiell om och endast om

$R_{a}R_{c}=R_{b}R_{d}$

där Ra , Rb , Rc , Rd är radierna i cirklarna som externt tangerar sidorna _{a ,} b , c , d respektive förlängningarna av de intilliggande två sidorna för varje _{sida .}

Flera karakteriseringar är kända i de fyra subtrianglarna som bildas av diagonalerna.

Kontaktpunkter och tangentlängder

En gential fyrhörning (i blått) och dess kontaktfyrhörning (i grönt) som förenar de fyra kontaktpunkterna mellan incirkeln och sidorna. Visade också tangens ackord som förenar motsatta kontaktpunkter (i rött) och tangentlängderna på sidorna

Incirkeln är tangent till varje sida vid en kontaktpunkt . Dessa fyra punkter definierar en ny fyrhörning inuti den initiala fyrhörningen: kontaktfyrhörningen, som är cyklisk eftersom den är inskriven i den initiala fyrhörningens incirkel.

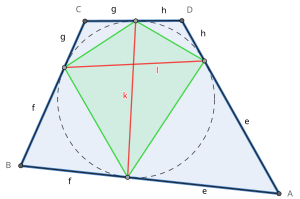
De åtta tangentlängderna ( e , f , g , h i figuren till höger) av en tangentiell fyrhörning är linjesegmenten från en vertex till kontaktpunkterna. Från varje vertex finns det två kongruenta tangentlängder.

De två tangens ackord ( k och l i figuren) i en tangentiell fyrhörning är linjesegmenten som förbinder kontaktpunkter på motsatta sidor. Dessa är också diagonalerna för kontaktfyrhörningen.

Område

Icke-trigonometriska formler

Arean K för en tangentiell fyrhörning ges av

$\displaystyle K=r\cdot s,$

där s är halvperimetern och r är inradius . En annan formel är

$\displaystyle K={\tfrac {1}{2}}{\sqrt {p^{2}q^{2}-( ac-bd)^{2}}}$

vilket ger arean i form av diagonalerna p , q och sidorna a , b , c , d på den tangentiella fyrhörningen.

Arean kan också uttryckas i termer av bara de fyra tangentlängderna . Om dessa är e , f , g , h , så har den tangentiella fyrhörningen arean

$\displaystyle K={\sqrt {(e+f+g+h)(efg+fgh+ghe+hef)}}.$

Dessutom kan arean av en tangentiell fyrhörning uttryckas i termer av sidorna a, b, c, d och de successiva tangentlängderna e, f, g, h som

$K={\sqrt {abcd-(eg-fh)^{2}}}.$

Eftersom t.ex. = fh om och endast om den tangentiella fyrhörningen också är cyklisk och därmed bicentrisk, visar detta att den maximala arean ${\sqrt {abcd}}$ inträffar om och endast om den tangentiella fyrhörningen är bicentrisk.

Trigonometriska formler

En trigonometrisk formel för arean i termer av sidorna a , b , c , d och två motsatta vinklar är

$\displaystyle K={\sqrt {abcd}}\sin {\frac {A+C}{2}}={\sqrt {abcd}}\sin {\frac {B+D}{2}} .$

För givna sidolängder är arean maximal när fyrhörningen också är cyklisk och därmed en bicentrisk fyrhörning . Då $K={\sqrt {abcd}}$ eftersom motsatta vinklar är kompletterande vinklar . Detta kan bevisas på annat sätt med hjälp av kalkyl .

En annan formel för arean av en tangentiell fyrhörning ABCD som involverar två motsatta vinklar är

$K=\left(IA\cdot IC+IB\cdot ID\right)\sin {\frac {A+C }{2}}$

där jag är mitten.

Faktum är att området kan uttryckas i termer av bara två intilliggande sidor och två motsatta vinklar som

$K=ab\sin {\frac {B}{2}}\csc {\frac {D}{2}}\sin {\frac {B+D}{2}}.$

Ännu en områdesformel är

$K={\tfrac {1}{2}}|(ac-bd)\tan {\theta }|,$

där θ är någon av vinklarna mellan diagonalerna. Denna formel kan inte användas när den tangentiella fyrhörningen är en drake, eftersom θ är 90° och tangentfunktionen inte är definierad.

Ojämlikheter

uppfyller arean av en tangentiell fyrhörning med sidorna a , b , c , d

$K\leq {\sqrt {abcd}}$

med jämlikhet om och bara om det är en bicentrisk fyrhörning .

Enligt TA Ivanova (1976) uppfyller semiperimetern s för en tangentiell fyrhörning

$s\geq 4r$

där r är inradius. Det finns likhet om och bara om fyrhörningen är en kvadrat . Det betyder att för området K = rs finns olikheten

$K\geq 4r^{2}$

med likhet om och endast om den tangentiella fyrhörningen är en kvadrat.

Partitionsegenskaper

Tangentiell fyrhörning med inradius r

De fyra linjesegmenten mellan incirkelns centrum och punkterna där den tangerar fyrhörningen delar upp fyrhörningen i fyra högra drakar .

Om en linje skär en tangentiell fyrhörning i två polygoner med lika stora ytor och lika omkretsar , så går den linjen genom mitten .

Inradius

Inradien i en tangentiell fyrhörning med på varandra följande sidor a , b , c , d ges av

$r={\frac {K}{s}}={\frac {K}{a+c}}={\frac {K}{ b+d}}$

där K är arean av fyrhörningen och s är dess halvperimeter. För en tangentiell fyrhörning med givna sidor är inradien maximal när fyrhörningen också är cyklisk (och därmed en bicentrisk fyrhörning ) .

När det gäller tangentlängderna har incirkeln radie

$\displaystyle r={\sqrt {\frac {efg+fgh+ghe+hef}{e+f+g+h}}}.$

Inradien kan också uttryckas i termer av avstånden från mitten I till hörnen på den tangentiella fyrhörningen ABCD . Om u = AI , v = BI , x = CI och y = DI , då

$r=2{\sqrt {\frac {(\sigma -uvx)(\sigma -vxy)(\sigma -xyu)(\sigma -yuv)}{uvxy(uv+xy )(ux+vy)(uy+vx)}}}$

där $\sigma ={\tfrac {1}{2}}(uvx+vxy+xyu+yuv)$ .

Om cirklarna i trianglarna ABC , BCD , CDA , DAB har radier $r_{1},r_{2},r_{3},r_{4}$ , då ges inradien för en tangentiell fyrhörning ABCD av

$r={\frac {G+{ \sqrt {G^{2}-4r_{1}r_{2}r_{3}r_{4}(r_{1}r_{3}+r_{2}r_{4})}}}{2( r_{1}r_{3}+r_{2}r_{4})}}$

där $G=r_{1}r_{2}r_{3}+r_{ 2}r_{3}r_{4}+r_{3}r_{4}r_{1}+r_{4}r_{1}r_{2}$ .

Vinkelformler

Om e , f , g och h är tangentlängderna från hörnen A , B , C respektive D till de punkter där incirkeln är tangent till sidorna av en tangentiell fyrhörning ABCD , så kan fyrhörningens vinklar beräknas från

$\sin {\frac {A}{2} }={\sqrt {\frac {efg+fgh+ghe+hef}{(e+f)(e+g)(e+h)}}},$

$\sin {\frac {B}{2}}={\sqrt {\frac {efg+fgh +ghe+hef}{(f+e)(f+g)(f+h)}}},$

$\sin {\frac {C}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(g+e)( g+f)(g+h)}}},$

$\sin {\frac {D}{2}}={\sqrt {\frac {efg+fgh+ghe+hef}{(h+e)(h+f)(h+g)}}} .$

Vinkeln mellan tangens ackord k och l ges av

$\sin {\varphi }={\sqrt {\frac {(e+f+g+h)(efg+fgh+ghe+hef)}{(e+f)(f+g)(g+ h)(h+e)}}}.$

Diagonaler

Om e , f , g och h är tangentlängderna från A , B , C respektive D till de punkter där incirkeln tangerar sidorna av en tangentiell fyrhörning ABCD , då är längderna på diagonalerna p = AC och q = BD är

$\displaystyle p={\sqrt {{\frac {e+g}{f+h}} {\Big (}(e+g)(f+h)+4fh{\Big )}}},$

$\displaystyle q={\sqrt {{\frac {f+h}{e+g}}{\Big (}(e+g)(f+h)+4eg{\Big )}}}.$

Tangens ackord

Om e , f , g och h är tangentlängderna för en tangentiell fyrhörning, så är längderna på tangenterna

$\displaystyle k={\ frac {2(efg+fgh+ghe+hef)}{\sqrt {(e+f)(g+h)(e+g)(f+h)}}},$

$\displaystyle l={\frac {2(efg+fgh+ghe +hef)}{\sqrt {(e+h)(f+g)(e+g)(f+h)}}}$

där tangensackordet av längden k förbinder sidorna av längderna a = e + f och c = g + h , och den med längden l förbinder sidorna av längderna b = f + g och d = h + e . Kvadratförhållandet för tangency ackord uppfyller

${\frac {k^{2}}{l^{2}}}={\frac {bd}{ac}}.$

De två tangency ackorden

• är vinkelräta om och endast om den tangentiella fyrhörningen också har en omsluten cirkel (den är bicentrisk ).
• ha lika långa om och endast om den tangentiella fyrhörningen är en drake .

Tangentackordet mellan sidorna AB och CD i en tangentiell fyrhörning ABCD är längre än den mellan sidorna BC och DA om och endast om bimedianen mellan sidorna AB och CD är kortare än den mellan sidorna BC och DA .

Om tangentiell fyrhörning ABCD har tangenspunkter W på AB och Y på CD , och om tangensackord WY skär diagonalen BD vid M , då förhållandet mellan tangentlängderna ${\tfrac {BW}{DY}}$ är lika med förhållandet ${\tfrac {BM}{DM}}$ för segmenten av diagonal BD .

Kolinjära punkter

Konstruktion av Newtonlinjen (i rött) för en tangentiell fyrhörning (i blått), som visar inriktningen av mitten I , mittpunkterna för diagonalerna M ₁ och M ₂ och mitten M ₃ av segmentet JK (i grönt) som sammanfogar skärningspunkten mellan motsatta sidor.

Om M ₁ och M ₂ är mittpunkterna för diagonalerna AC respektive BD i en tangentiell fyrhörning ABCD med mitten I , och om paren av motsatta sidor möts vid J och K med M ₃ som mittpunkten av JK , då är punkterna M ₃ , M1 _{_} , I och M2 _{_} är kolinjära . Linjen som innehåller dem är fyrhörningens Newtonlinje .

Om förlängningarna av motsatta sidor i en tangentiell fyrhörning skär vid J och K , och förlängningarna av motsatta sidor i dess kontaktfyrhörning skär vid L och M , då är de fyra punkterna J , L , K och M kolinjära.

En tangentiell fyrhörning är uppdelad i fyra trianglar som möts i dess centrum I , deras ortocenter (lila) och skärningspunkten mellan diagonalerna P (i grönt) är alla kolinjära.

Om incirkeln tangerar sidorna AB , BC , CD , DA vid T ₁ , T ₂ , T ₃ , T ₄ respektive, och om N ₁ , N ₂ , N ₃ , N ₄ är de isotomiska konjugaten av dessa punkter med med avseende på motsvarande sidor (det vill säga AT ₁ = BN ₁ och så vidare), så definieras Nagelpunkten för den tangentiella fyrhörningen som skärningspunkten mellan linjerna N ₁ N ₃ och N ₂ N ₄ . Båda dessa linjer delar omkretsen av fyrhörningen i två lika delar. Ännu viktigare är att Nagel-punkten N , "areacentroiden" G och mitten I är kolinjära i denna ordning, och NG = 2 GI . Denna linje kallas Nagel-linjen för en tangentiell fyrhörning.

I en tangentiell fyrhörning ABCD med incenter I och där diagonalerna skär varandra vid P , låt H _X , H _Y , H _Z , H _W vara ortocenterna för trianglarna AIB , BIC , CID , DIA . Då är punkterna P , H _X , H _Y , H _Z , H _W kolinjära.

Samtidiga och vinkelräta linjer

De två diagonalerna och de två tangensackorden är samtidiga . Ett sätt att se detta är som ett begränsande fall av Brianchons sats , som säger att en hexagon vars alla sidor tangerar ett enda koniskt snitt har tre diagonaler som möts i en punkt. Från en tangentiell fyrhörning kan man bilda en hexagon med två 180° vinklar, genom att placera två nya hörn vid två motsatta tangenspunkter; alla sex sidorna av denna hexagon ligger på linjer som tangerar den inskrivna cirkeln, så dess diagonaler möts vid en punkt. Men två av dessa diagonaler är desamma som diagonalerna för den tangentiella fyrhörningen, och den tredje diagonalen av hexagonen är linjen genom två motsatta tangenspunkter. Att upprepa samma argument med de andra två tangenspunkterna fullbordar beviset på resultatet.

Om förlängningarna av motsatta sidor i en tangentiell fyrhörning skär vid J och K , och diagonalerna skär vid P , är JK vinkelrät mot förlängningen av IP där I är mitten.

I mitten

Mitten av en tangentiell fyrhörning ligger på dess Newtonlinje (som förbinder diagonalernas mittpunkter).

Förhållandet mellan två motsatta sidor i en tangentiell fyrhörning kan uttryckas i termer av avstånden mellan mitten I och hörnen enl.

${\frac {AB}{CD}}={\frac {IA\cdot IB}{IC\cdot ID}},\quad \quad {\frac {BC}{DA}}={\frac { IB\cdot IC}{ID\cdot IA}}.$

Produkten av två intilliggande sidor i en tangentiell fyrhörning ABCD med mitten I uppfyller

$AB\cdot BC=IB^{2}+{\frac {IA\cdot IB\cdot IC}{ID}}.$

Om I är mitten av en tangentiell fyrhörning ABCD , då

$IA\cdot IC+IB\cdot ID={\sqrt {AB\cdot BC\cdot CD\cdot DA}}.$

Incenter I i en tangentiell fyrhörning ABCD sammanfaller med "vertex centroid" av fyrhörningen om och endast om

$IA\cdot IC=IB\cdot ID.$

Om M _p och M _q är mittpunkterna för diagonalerna AC respektive BD i en tangentiell fyrhörning ABCD med mitten I , då

${\frac {IM_{p}}{IM_{q}}}={\frac {IA\ cdot IC}{IB\cdot ID}}={\frac {e+g}{f+h}}$

där e , f , g och h är tangentlängderna vid A , B , C respektive D. Genom att kombinera den första likheten med en tidigare egenskap, sammanfaller den tangentiella fyrhörningens "vertexcentroid" med incenter om och endast om incenter är mittpunkten av linjesegmentet som förbinder diagonalernas mittpunkter.

Om en fyrstavslänkning görs i form av en tangentiell fyrhörning, kommer den att förbli tangentiell oavsett hur kopplingen böjs, förutsatt att fyrhörningen förblir konvex. (Således, till exempel, om en kvadrat deformeras till en romb förblir den tangentiell, dock till en mindre incirkel). Om en sida hålls i ett fast läge, då fyrhörningen böjs, spårar mitten ut en cirkel med radien ${\sqrt {abcd}}/s$ där a,b,c ,d är sidorna i följd och s är semiperimetern.

Karakteriseringar i de fyra subtrianglarna

Chao och Simeonovs karaktärisering i termer av cirklarnas radier inom var och en av fyra trianglar

I de icke-överlappande trianglarna APB , BPC , CPD , DPA som bildas av diagonalerna i en konvex fyrhörning ABCD , där diagonalerna skär varandra vid P , finns följande karakteriseringar av tangentiella fyrhörningar.

Låt r ₁ , r ₂ , r ₃ och r ₄ beteckna radierna för cirklarna i de fyra trianglarna APB , BPC , CPD , respektive DPA . Chao och Simeonov bevisade att fyrhörningen är tangentiell om och bara om

${\frac {1}{r_{1}}}+{\frac {1}{r_{3}}}={\frac {1}{r_{2}}}+{\frac {1 }{r_{4}}}.$

Denna karaktärisering hade redan bevisats fem år tidigare av Vaynshtejn. I lösningen på hans problem gavs en liknande karaktärisering av Vasilyev och Senderov. Om h ₁ , h ₂ , h ₃ och h ₄ anger höjderna i samma fyra trianglar (från diagonalskärningen till sidorna av fyrhörningen), så är fyrhörningen tangentiell om och endast om

${\frac {1}{h_{1}}}+{\frac {1}{h_{3}}}={\frac {1}{h_{2}}}+{\frac {1 }{h_{4}}}.$

En annan liknande karaktärisering gäller exradii r _a , r _b , r _c och r _d i samma fyra trianglar (de fyra excirklarna är var och en tangent till en sida av fyrhörningen och förlängningarna av dess diagonaler). En fyrhörning är tangentiell om och endast om

${\frac {1}{r_{a}}}+{\frac {1}{r_{c}}}={\frac {1}{r_{b}}}+{\frac {1 }{r_{d}}}.$

Om R ₁ , R ₂ , R ₃ och R ₄ anger radierna i de omslutna cirklarna av trianglarna APB , BPC , CPD , respektive DPA , så är fyrhörningen ABCD tangentiell om och endast om

$R_{1}+R_{3}=R_{2}+R_{4}.$

År 1996 var Vaynshtejn förmodligen den första som bevisade en annan vacker karaktärisering av tangentiella fyrhörningar, som senare har dykt upp i flera tidningar och webbplatser. Det sägs att när en konvex fyrhörning delas i fyra icke-överlappande trianglar av sina två diagonaler, så är centrumen för de fyra trianglarna koncykliska om och endast om fyrhörningen är tangentiell. Faktum är att incenterna bildar en ortodiagonal cyklisk fyrhörning . Ett relaterat resultat är att cirklarna kan bytas ut mot cirklarna till samma trianglar (tangens till sidorna av fyrhörningen och förlängningarna av dess diagonaler). Således är en konvex fyrhörning tangentiell om och endast om excenterna i dessa fyra excirklar är hörn av en cyklisk fyrhörning .

En konvex fyrhörning ABCD , med diagonaler som skär varandra vid P , är tangentiell om och endast om de fyra excenterna i trianglarna APB , BPC , CPD , och DPA mittemot hörnen B och D är koncykliska. Om Ra _Rb , , Rc _exradii och Rd är _om i trianglarna APB , BPC , CPD respektive DPA mittemot hörnen så _B och D , är ett annat villkor att fyrhörningen är tangentiell om och endast

${\frac {1}{R_{a}}}+{\frac {1}{R_{c}}}={\frac {1}{R_{b}}}+{\frac {1 }{R_{d}}}.$

Vidare är en konvex fyrhörning ABCD med diagonaler som skär vid P tangentiell om och endast om

${\frac {a}{\triangle (APB)}}+{ \frac {c}{\triangle (CPD)}}={\frac {b}{\triangle (BPC)}}+{\frac {d}{\triangle (DPA)}}$

där ∆( APB ) är arean av triangeln APB .

Beteckna segmenten som den diagonala skärningspunkten P delar diagonalen AC i som AP = p ₁ och PC = p ₂ , och på samma sätt delar P diagonalen BD i segmenten BP = q ₁ och PD = q ₂ . Då är fyrhörningen tangentiell om och endast om någon av följande likheter är sann:

$ap_{2}q_{2}+cp_{1}q_{1}=bp_{1}q_{ 2}+dp_{2}q_{1}$

eller

${\frac {(p_{1}+q_{1}-a)(p_{2}+q_ {2}-c)}{(p_{1}+q_{1}+a)(p_{2}+q_{2}+c)}}={\frac {(p_{2}+q_{1 }-b)(p_{1}+q_{2}-d)}{(p_{2}+q_{1}+b)(p_{1}+q_{2}+d)}}$

eller

${\frac {(a+p_{1}-q_{1})(c+p_{2}-q_{2})}{(a-p_{1}+q_{1})(c -p_{2}+q_{2})}}={\frac {(b+p_{2}-q_{1})(d+p_{1}-q_{2})}{(b-p_ {2}+q_{1})(d-p_{1}+q_{2})}}.$

Villkor för att en tangentiell fyrhörning ska vara en annan typ av fyrhörning

Romb

En tangentiell fyrhörning är en romb om och endast om dess motsatta vinklar är lika.

Drake

En tangentiell fyrhörning är en drake om och endast om något av följande villkor är sant:

• Ytan är hälften av produkten av diagonalerna .
• Diagonalerna är vinkelräta .
• De två linjesegmenten som förbinder motsatta tangenspunkter har lika långa längder.
• Ett par motsatta tangentlängder har lika långa.
• Bimedianerna har lika långa .
• Produkterna från motsatta sidor är lika.
• Mitten av incirkeln ligger på diagonalen som är symmetriaxeln.

Bicentrisk fyrhörning

En bicentrisk fyrhörning ABCD : kontaktfyrhörningen (rosa) är ortodiagonal.

Om incirkeln är tangent till sidorna AB , BC , CD , DA vid W , X , Y , Z respektive, så är en tangentiell fyrhörning ABCD också cyklisk (och därmed bicentrisk ) om och bara om något av följande villkor gäller:

• WY är vinkelrät mot XZ
• $AW\cdot CY=BW\cdot DY$
• ${\frac {AC}{BD}}={\frac {AW+CY}{BX+DZ}}$

Den första av dessa tre betyder att kontaktfyrsidan WXYZ är en ortodiagonal fyrhörning .

En tangentiell fyrhörning är bicentrisk om och endast om dess inradius är större än den för någon annan tangentiell fyrhörning med samma sekvens av sidolängder.

Tangentiell trapets

Om incirkeln tangerar sidorna AB och CD vid W respektive Y , är en tangentiell fyrhörning ABCD också en trapets med parallella sidor AB och CD om och endast om

$AW\cdot DY=BW\cdot CY$

och AD och BC är de parallella sidorna av en trapets om och endast om

$AW\cdot BW=CY\cdot DY.$

Se även

• Omskriven cirkel
• Extangentiell fyrhörning
• Tangentiell triangel
• Tangentiell polygon

externa länkar

• Weisstein, Eric W. , "Tangential Quadrilateral" , MathWorld