D 6 polytop
 6-demikub |
 6-ortoplex |
I 6-dimensionell geometri finns det 47 enhetliga polytoper med D 6- symmetri, varav 16 är unika och 31 delas med B 6 -symmetri. Det finns två vanliga former, 6-ortoplex och 6-demikub med 12 respektive 32 hörn.
De kan visualiseras som symmetriska ortografiska projektioner i Coxeter-plan i D 6 Coxeter-gruppen och andra undergrupper.
Grafer
Symmetriska ortografiska projektioner av dessa 16 polytoper kan göras i D 6 , D 5 , D 4 , D 3 , A 5 , A 3 , Coxeter planen . A k har [k+1] symmetri, Dk har [ 2(k-1)] symmetri. B 6 ingår också även om bara hälften av dess [12] symmetri finns i dessa polytoper.
Dessa 16 polytoper visas var och en i dessa 7 symmetriplan, med hörn och kanter ritade, och hörn färgade av antalet överlappande hörn i varje projektiv position.
| # | Coxeter plan grafer |
Coxeter diagram Namn |
||||||
|---|---|---|---|---|---|---|---|---|
|
B 6 [12/2] |
D 6 [10] |
D 5 [8] |
D 4 [6] |
D 3 [4] |
A 5 [6] |
A 3 [4] |
||
| 1 |  |
 |
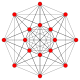 |
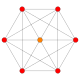 |
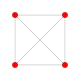 |
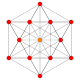 |
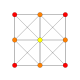 |
= 6-demikub Hemihexeract (hax) |
| 2 |  |
 |
 |
 |
 |
 |
 |
= cantic 6-kub Trunkated hemihexeract (thax) |
| 3 |  |
 |
 |
 |
 |
 |
 |
= runkisk 6-kub Liten romberad hemihexeract (sirhax) |
| 4 |  |
 |
 |
 |
 |
 |
 |
= sterisk 6-kub liten prismatad hemihexeract (sophax) |
| 5 |  |
 |
 |
 |
 |
 |
 |
= pentisk 6-kub Liten cellad demihexeract (sochax) |
| 6 |  |
 |
 |
 |
 |
 |
 |
= runcicantic 6-kub Stor romberad hemihexeract (girhax) |
| 7 |  |
 |
 |
 |
 |
 |
 |
= sterikantisk 6-kub Prismatotruncated hemihexeract (pitax) |
| 8 |  |
 |
 |
 |
 |
 |
 |
= steriruncic 6-kub Prismatorhombated hemihexeract (prohax) |
| 9 |  |
 |
 |
 |
 |
 |
 |
= Stericantic 6-kuber Cellitruncated hemihexeract (cathix) |
| 10 |  |
 |
 |
 |
 |
 |
 |
= Pentiruncic 6-kuber Cellirhombated hemihexeract (crohax) |
| 11 |  |
 |
 |
 |
 |
 |
 |
= Pentisterisk 6-kub celliprismatad hemihexeract (cophix) |
| 12 |  |
 |
 |
 |
 |
 |
 |
= Steriruncicantic 6-kub Stor prismatad hemihexeract (gophax) |
| 13 |  |
 |
 |
 |
 |
 |
 |
= Pentiruncicantic 6-kuber Celligreatorhombated hemihexeract (cagrohax) |
| 14 |  |
 |
 |
 |
 |
 |
 |
= Pentistericantic 6-kuber Celliprismatotruncated hemihexeract (capthix) |
| 15 |  |
 |
 |
 |
 |
 |
 |
= Pentisteriruncic 6-kub celliprismatorhomberad hemihexeract (caprohax) |
| 16 |  |
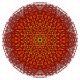 |
 |
 |
 |
 |
 |
= Pentisteriruncicantic 6-kub Stor cellad hemihexeract (gochax) |
-
HSM Coxeter :
- HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
-
Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
- (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
- Klitzing, Richard. "6D enhetliga polytoper (polypeta)" .