Verkligt koordinatutrymme

Kartesiska koordinater identifierar punkter på det euklidiska planet med par av reella tal

I matematik är det reella koordinatutrymmet för dimension n , betecknat R ⁿ eller $\mathbb {R} ^{n}$ , mängden av n -tuplarna av reella tal , det vill säga mängden av alla sekvenser av n reella tal. Med komponentvis addition och skalär multiplikation är det ett verkligt vektorrum , och dess element kallas koordinatvektorer .

Koordinaterna över vilken bas som helst av elementen i ett reellt vektorrum bildar ett reellt koordinatutrymme av samma dimension som vektorrummets. På liknande sätt bildar de kartesiska koordinaterna för punkterna i ett euklidiskt utrymme med dimension n ett verkligt koordinatrum av dimension n .

Dessa en till en överensstämmelse mellan vektorer, punkter och koordinatvektorer förklarar namnen på koordinatutrymme och koordinatvektor . Det gör det möjligt att använda geometriska termer och metoder för att studera verkliga koordinatutrymmen, och omvänt att använda metoder för kalkyl i geometri. Detta tillvägagångssätt för geometri introducerades av René Descartes på 1600-talet. Det används ofta, eftersom det gör det möjligt att lokalisera punkter i euklidiska utrymmen och beräkna med dem.

Definition och strukturer

För alla naturliga tal n består mängden Rn ⁾ av alla n - tuplar av reella tal ( R . Det kallas det " n -dimensionella verkliga rummet" eller det "verkliga n -rummet".

Ett element av R ⁿ är alltså en n -tuppel, och skrivs

$$(x_{1},x_{2},\ldots ,x_{n})$$

där varje x _i är ett reellt tal. Så Rn ^, i multivariabelkalkyl är domänen för en funktion av flera reella variabler och codomänen för en funktion med reell vektorvärderad funktion delmängder av för några n .

Det verkliga n -utrymmet har flera ytterligare egenskaper, särskilt:

• Med komponentvis addition och skalär multiplikation är det ett verkligt vektorrum . Varje n -dimensionellt reellt vektorrum är isomorft till det.
• Med punktprodukten (summan av termen för termprodukt av komponenterna) är det ett inre produktrum . Varje n -dimensionellt verkligt inre produktutrymme är isomorft för det.
• Som varje inre produktutrymme är det ett topologiskt utrymme och ett topologiskt vektorrum .
• Det är ett euklidiskt utrymme och ett verkligt affint utrymme , och varje euklidiskt eller affint utrymme är isomorft till det.
• Det är ett analytiskt grenrör och kan betraktas som prototypen av alla Rn ^grenrör , eftersom ett grenrör per definition är, nära varje punkt, isomorft till en öppen delmängd av .
• Det är en algebraisk variant , och varje verklig algebraisk variant är en delmängd av Rn ^.

Dessa egenskaper och strukturer hos Rn ^statistik gör det grundläggande inom nästan alla områden av matematik och deras tillämpningsområden, såsom , sannolikhetsteori och många delar av fysiken .

Domänen för en funktion av flera variabler

Huvudartiklar: Multivariabelkalkyl och Real multivariabelfunktion

Rn ^Vilken funktion som helst f ( x ₁ , x ₂ , ..., x _n ) av n reella variabler kan betraktas som en funktion på (det vill säga med Rn ^. som sin domän ) Användningen av det reella n -utrymmet, istället för flera variabler som betraktas separat, kan förenkla notation och föreslå rimliga definitioner. Betrakta, för n = 2 , en funktionssammansättning av följande form:

$$F(t)=f(g_{1}(t),g_{2}(t)),$$

där funktionerna g ₁ och g ₂ är kontinuerliga . Om

• ∀ x ₁ ∈ R : f ( x ₁ , ·) är kontinuerlig (med x ₂ )
• ∀ x ₂ ∈ R : f (·, x ₂ ) är kontinuerlig (med x ₁ )

då är F inte nödvändigtvis kontinuerligt. Kontinuitet är ett starkare villkor: kontinuiteten för f i den naturliga R ² -topologin ( diskuteras nedan ), även kallad multivariabel kontinuitet , vilket är tillräckligt för kontinuitet i sammansättningen F .

Vektor utrymme

Koordinatutrymmet R ⁿ bildar ett n -dimensionellt vektorrum över fältet av reella tal med tillägg av linjäritetsstrukturen och betecknas ofta fortfarande R ⁿ . Operationerna på Rn som ^ett vektorrum definieras typiskt av

$$\mathbf {x} +\mathbf {y} =(x_{1}+y_{1} ,x_{2}+y_{2},\ldots ,x_{n}+y_{n})$$

$$\alpha \mathbf {x} =(\alpha x_{1},\alpha x_{2},\ldots ,\alpha x_{n}).$$

Nollvektorn ges av

$$\mathbf {0} =(0,0,\ldots ,0)$$

och den additiva inversen av vektorn x ges av

$$-\mathbf {x} =(-x_{1},-x_{2},\ldots ,-x_{n}).$$

Denna struktur är viktig eftersom varje n -dimensionellt reellt vektorrum är isomorft med vektorrummet Rn ^.

Matrisnotation

Huvudartikel: Matrix (matematik)

I standardmatrisnotation skrivs varje element i ^Rn vanligtvis som en kolumnvektor

$$\mathbf {x} ={\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix }}$$

och ibland som en radvektor :

$$\mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}.$$

Koordinatutrymmet Rn ^de kan då tolkas som utrymmet för alla n × 1 kolumnvektorer , eller alla 1 × n radvektorer med vanliga matrisoperationerna addition och skalär multiplikation .

Linjära transformationer från R ⁿ till Rm ^som kan sedan skrivas som m × n matriser verkar på elementen i R ⁿ via vänstermultiplikation (när elementen i Rn ^när är kolumnvektorer) och på element i ^Rm via högermultiplikation ( de är radvektorer). Formeln för vänstermultiplikation, ett specialfall av matrismultiplikation , är:

$$(A{\mathbf {x} })_{k}=\summa _{l=1}^{n}A_{kl} x_{l}$$

All linjär transformation är en kontinuerlig funktion (se nedan ). En matris definierar också en öppen karta från Rn ^med till Rm ^är om och endast om matrisens rangordning lika m .

Standardbas

Huvudartikel: Standardbas

Koordinatutrymmet Rn ^: kommer med en standardbas

$${\begin{aligned}\mathbf {e} _{1}& =(1,0,\ldots ,0)\\\mathbf {e} _{2}&=(0,1,\ldots ,0)\\&{}\;\;\vdots \\\mathbf { e} _{n}&=(0,0,\ldots ,1)\end{aligned}}$$

För att se att detta är en grund, notera att en godtycklig vektor i R ⁿ kan skrivas unikt i formen

$$\mathbf {x} =\sum _{i=1}^{n}x_{i}\mathbf {e} _{i}.$$

Geometriska egenskaper och användningsområden

Orientering

Rn ^Det faktum att reella tal , till skillnad från många andra fält , utgör ett ordnat fält ger en orienteringsstruktur på . Varje linjär karta med full rang av R ⁿ till sig själv antingen bevarar eller omvänder orienteringen av rymden beroende på tecknet för determinanten för dess matris. Om man permuterar koordinater (eller, med andra ord, element av basen), kommer den resulterande orienteringen att bero på permutationens paritet .

Diffeomorfismer av Rn ^Jacobian eller domäner i den klassificeras också till orienteringsbevarande och orienteringsreverserande, genom att de undviker noll . Det har viktiga konsekvenser för teorin om differentialformer , vars tillämpningar inkluderar elektrodynamik .

En annan manifestation av denna struktur är att punktreflektionen i R ⁿ har olika egenskaper beroende på jämnheten hos n . För jämn n bevarar den orienteringen, medan den för udda n är omvänd (se även felaktig rotation ) .

Affint utrymme

Ytterligare information: Affine space

Rn ^som förstås som ett affint utrymme är samma utrymme, där R ⁿ ett vektorrum verkar genom translationer . Omvänt måste en vektor förstås som en " skillnad mellan två punkter", vanligtvis illustrerad av ett riktat linjesegment som förbinder två punkter. Distinktionen säger att det inte finns något kanoniskt val av var ursprunget ska gå i ett affint n -utrymme, eftersom det kan översättas var som helst.

Konvexitet

n - simplexet (se nedan ) är den konvexa standarduppsättningen, som mappas till varje polytop, och är skärningspunkten mellan det standard ( n + 1) affina hyperplanet (standardaffina rymden) och standarden ( n + 1) orthant (standard) kon).

Ytterligare information: Konvex analys

I ett verkligt vektorrum, såsom Rn ^av , kan man definiera en konvex kon , som innehåller alla icke-negativa linjära kombinationer dess vektorer. Motsvarande koncept i ett affint utrymme är en konvex uppsättning , som endast tillåter konvexa kombinationer (icke-negativa linjära kombinationer som summerar till 1).

universell algebras språk är ett vektorrum en algebra över det universella vektorrummet R ^∞ av ändliga sekvenser av koefficienter, motsvarande ändliga summor av vektorer, medan ett affinutrymme är en algebra över det universella affina hyperplanet i detta utrymme (av finita sekvenser summerande till 1), en kon är en algebra över den universella orthanten (av finita sekvenser av icke-negativa tal), och en konvex mängd är en algebra över den universella simplexen (av finita sekvenser av icke-negativa tal summerande till 1). Detta geometriserar axiomen i termer av "summor med (eventuella) begränsningar av koordinaterna".

Ett annat koncept från konvex analys är en konvex funktion från R ⁿ till reella tal, som definieras genom en olikhet mellan dess värde på en konvex kombination av punkter och summan av värden i de punkter med samma koefficienter.

Euklidiskt utrymme

Huvudartiklar: Euklidiskt rymd och kartesiskt koordinatsystem

Den prickiga produkten

$$\mathbf {x} \cdot \mathbf {y} =\summa _{ i=1}^{n}x_{i}y_{i}=x_{1}y_{1}+x_{2}y_{2}+\cdots +x_{n}y_{n}$$

definierar normen | x | = √ x ⋅ x på vektorrummet R ⁿ . Om varje vektor har sin euklidiska norm , då är avståndet för valfritt par av punkter

$$d(\mathbf {x} ,\mathbf {y} )=\|\mathbf {x } -\mathbf {y} \|={\sqrt {\sum _{i=1}^{n}(x_{i}-y_{i})^{2}}}$$

definieras och tillhandahåller en Rn ^metrisk rymdstruktur på förutom dess affina struktur.

Rn ^gäller vektorrumsstrukturen antas prickprodukten och det euklidiska avståndet vanligtvis existera i utan speciella förklaringar. Det verkliga n -utrymmet och ett euklidiskt n -rum är dock strängt taget distinkta objekt. Varje euklidiskt n -rum har ett koordinatsystem där prickprodukten och det euklidiska avståndet har den form som visas ovan, kallad kartesisk . Men det finns många kartesiska koordinatsystem på ett euklidiskt utrymme.

Omvänt definierar ovanstående formel för den euklidiska metriken den euklidiska standardstrukturen på Rn ^, men det är inte den enda möjliga. Egentligen definierar vilken positiv-definitiv kvadratisk form q som helst sitt eget "avstånd" √ q ( x − y ) , men den skiljer sig inte mycket från den euklidiska i den meningen att

$$\exists C_{1}>0,\ \exists C_{2}>0,\ \forall \mathbf {x} ,\mathbf {y} \in \mathbb {R} ^{n}:C_{ 1}d(\mathbf {x} ,\mathbf {y} )\leq {\sqrt {q(\mathbf {x} -\mathbf {y} )}}\leq C_{2}d(\mathbf {x } ,\mathbf {y} ).$$

En sådan ändring av metriken bevarar en del av dess egenskaper, till exempel egenskapen att vara ett komplett metriskt utrymme . Detta innebär också att all linjär transformation i full rang av R ⁿ , eller dess affina transformation , inte förstorar avstånden mer än med någon fast C ₂ , och inte gör avstånden mindre än 1 / C ₁ gånger, ett fast ändligt antal gånger mindre .

Ovannämnda ekvivalens av metriska funktioner förblir giltig om √ q ( x − y ) ersätts med M ( x − y ) , där M är en konvex positiv homogen funktion av grad 1, dvs en vektornorm (se Minkowski-avstånd för användbara exempel) . På grund av detta faktum att någon "naturlig" metrik på R ⁿ inte skiljer sig särskilt från den euklidiska metriken, skiljer sig R ^{n inte alltid från ett euklidiskt} n -rum ens i professionella matematiska arbeten.

I algebraisk och differentialgeometri

Även om definitionen av ett grenrör inte kräver att dess modellutrymme ska vara ^Rn , är detta val det vanligaste och nästan exklusiva i differentialgeometri .

Å andra sidan anger Whitneys inbäddningssatser att alla verkliga differentierbara m -dimensionella grenrör kan bäddas in i R ^{2 m} .

Andra framträdanden

Andra strukturer som betraktas på Rn ⁾ inkluderar en av ett pseudo-euklidiskt utrymme , symplektisk struktur (jämn n och kontaktstruktur (udda n ). Alla dessa strukturer, även om de kan definieras på ett koordinatfritt sätt, tillåter standardformer (och någorlunda enkla) i koordinater.

Rn ^; är också ett reellt vektorunderrum av ^Cn som är invariant mot komplex konjugation se även komplexisering .

Polytoper i R ⁿ

Se även: Linjär programmering och konvex polytop

Det finns tre familjer av polytoper som har enkla representationer i R ⁿ -rum, för vilket n som helst , och som kan användas för att visualisera vilket affint koordinatsystem som helst i ett verkligt n -rum. Vertices i en hyperkub har koordinater ( x ₁ , x ₂ , ..., x _n ) där varje x _k antar ett av endast två värden, typiskt 0 eller 1. Däremot kan två valfria tal väljas istället för 0 och 1 , till exempel −1 och 1. En n -hyperkub kan ses som den kartesiska produkten av n identiska intervall (som enhetsintervallet [0,1] ) på den reella linjen. Som en n -dimensionell delmängd kan den beskrivas med ett system med 2 n olikheter :

$${\begin{matrix}0\leq x_{1}\leq 1\\\vdots \\0\leq x_{n}\leq 1\end{matris }}$$

för [0,1] och

$${\begin{matrix}|x_{1}|\leq 1\\\vdots \\|x_{n}|\leq 1\end{matrix}}$$

för [−1,1] .

Varje vertex av korspolytopen har, för vissa k , xk k _- koordinaten lika med ±1 och alla andra koordinater lika med 0 (så att det är den : te standardbasvektorn upp till tecken ). Detta är en dubbel polytop av hyperkub. Som en n -dimensionell delmängd kan den beskrivas med en enda olikhet som använder absolutvärdesoperationen :

$$\sum _{k=1}^{n}|x_{k}|\leq 1\,,$$

men detta kan uttryckas med ett system med 2 ⁿ linjära olikheter också.

Den tredje polytopen med helt enkelt uppräknade koordinater är standardsimplexet , vars hörn är n standardbasvektorer och ursprunget (0, 0, ..., 0) . Som en n -dimensionell delmängd beskrivs den med ett system av n + 1 linjära olikheter:

$${\begin{matrix}0\leq x_{1}\\\vdots \\0\leq x_{n}\\\summa \ gränser _{k=1}^{n}x_{k}\leq 1\end{matris}}$$

Ersättning av alla "≤" med "<" ger interiörer av dessa polytoper.

Topologiska egenskaper

Den topologiska strukturen av Rn ^vanlig (kallad standardtopologi , euklidisk topologi eller topologi ) kan erhållas inte bara från kartesisk produkt . Den är också identisk med den naturliga topologin som induceras av euklidisk metrik som diskuterats ovan : en mängd är öppen i den euklidiska topologin om och bara om den innehåller en öppen boll runt var och en av dess punkter. Rn ^. är också ett linjärt topologiskt utrymme (se kontinuiteten i linjära kartor ovan), och det finns bara en möjlig (icke-trivial) topologi som är kompatibel med dess linjära struktur Rn ^Eftersom det finns många öppna linjära kartor från Rn ^kan till sig själv som inte är isometrier , det finnas många euklidiska strukturer på som motsvarar samma topologi. Egentligen beror det inte mycket på den linjära strukturen: det finns många icke-linjära Rn ^{diffeomorfismer} ( och andra homeomorfismer) av på sig själv, eller dess delar som en euklidisk öppen boll eller det inre av en hyperkub ).

R ⁿ har den topologiska dimensionen n . Ett viktigt resultat på topologin av R ⁿ , som är långt ifrån ytligt, är Brouwers invarians av domän . Varje delmängd av Rn ^Rn ( ^till med dess subrymdstopologi ) som är homeomorf en annan öppen delmängd av är själv öppen. En omedelbar konsekvens av detta är att R ^m inte är homeomorf till R ⁿ om m ≠ n – ett intuitivt "uppenbart" resultat som ändå är svårt att bevisa.

Rn ⁱ motsats till en naiv uppfattning, är det möjligt att kartlägga ett mindre dimensionellt [ verkligt utrymme kontinuerligt och surjektivt på . En kontinuerlig (men inte jämn) rymdfyllande kurva (en bild av R1 ^. ) är möjlig

Exempel

Tom kolumnvektor, det enda elementet i R 0

n ≤ 1

Fall av 0 ≤ n ≤ 1 ger inget nytt: R ¹ är den reella linjen , medan R ⁰ (utrymmet som innehåller den tomma kolumnvektorn) är en singelton , förstås som ett nollvektorutrymme . Det är dock användbart att inkludera dessa som triviala fall av teorier som beskriver olika n .

n = 2

Både hyperkub och korspolytop i R ² är kvadrater , men koordinater för hörn är ordnade på olika sätt

Ytterligare information: Tvådimensionellt utrymme

Se även: SL2(R)

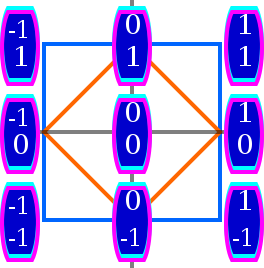
Fallet med ( x,y ) där x och y är reella tal har utvecklats som det kartesiska planet P . Ytterligare struktur har fästs med euklidiska vektorer som representerar riktade linjesegment i P . Planet har också utvecklats som fältförlängningen $\mathbb {C}$ genom att lägga till rötter av X ² + 1 = 0 till det reella fältet $\mathbb {R} .$ Roten i verkar på P som ett kvartsvarv med moturs orientering. Denna rot genererar gruppen {i, –1, –i, +1} ≅ ℤ/4ℤ. När ( x,y ) skrivs x + y i är det ett komplext tal .

En annan gruppåtgärd med ℤ/2ℤ, där aktören har uttryckts som j, använder linjen y = x för involutionen av att vända planet ( x,y ) ↦ ( y,x ), ett utbyte av koordinater. I det här fallet skrivs punkter i P x + y j och kallas delade-komplexa tal . Dessa tal, med koordinatvis addition och multiplikation enligt jj =+1, bildar en ring som inte är ett fält.

En annan ringstruktur på P använder ett nilpotent e för att skriva x + y e för ( x,y ) . Verkan av e på P reducerar planet till en linje: Det kan dekomponeras i projektionen i x-koordinaten och sedan kvartsvända resultatet till y-axeln: e ( x + y e) = x e eftersom e ² = 0. Ett tal x + y e är ett dubbeltal . De dubbla talen bildar en ring, men eftersom e inte har någon multiplikativ invers, genererar den inte en grupp så åtgärden är inte en gruppåtgärd.

Exklusive (0,0) från P ger [ x : y ] projektiva koordinater som beskriver den verkliga projektiva linjen, ett endimensionellt rum. Eftersom ursprunget är exkluderat, finns åtminstone ett av förhållandena x / y och y / x . Sedan [ x : y ] = [ x / y : 1] eller [ x : y ] = [1 : y / x ]. Den projektiva linjen P ¹ ( R ) är ett topologiskt grenrör som täcks av två koordinatdiagram , [ z : 1 ] → z eller [1 : z ] → z , som bildar en atlas . För punkter som täcks av båda diagrammen övergångsfunktionen multiplikativ inversion på ett öppet område av punkten, vilket ger en homeomorfism som krävs i en mångfald. En tillämpning av den verkliga projektiva linjen finns i Cayley-Klein metrisk geometri.

n = 3

Kub (hyperkuben) och oktaeder (korspolytopen) av R ³ . Koordinater visas inte

Huvudartikel: Tredimensionellt utrymme

n = 4

Ytterligare information: Fyrdimensionellt utrymme

R ⁴ kan föreställas med det faktum att 16 punkter ( x ₁ , x ₂ , x ₃ , x ₄ ) , där varje x _k är antingen 0 eller 1, är hörn av en tesserakt (bilden), 4-hyperkuben (se ovan ).

Den första stora användningen av R ⁴ är en rumtidsmodell : tre rumsliga koordinater plus en temporal . Detta förknippas vanligtvis med relativitetsteorin , även om fyra dimensioner användes för sådana modeller sedan Galilei . Valet av teori leder dock till en annan struktur: i galileisk relativitet är t - koordinaten privilegierad, men i einsteinsk relativitet är det inte det. Special relativitetsteori utspelar sig i Minkowskis rymden . Allmän relativitetsteori använder krökta utrymmen, som kan ses som R ⁴ med en krökt metrisk för de flesta praktiska ändamål. Ingen av dessa strukturer ger ett (positivt-definitivt ) mått på R4 ^.

Euklidisk R ⁴ lockar också matematikers uppmärksamhet, till exempel på grund av dess relation till quaternions , en 4-dimensionell verklig algebra själva. Se rotationer i 4-dimensionell euklidisk rymd för lite information.

I differentialgeometri är n = 4 det enda fallet där Rn ^. medger en icke-standardiserad differentialstruktur : se exotiska R ⁴

Normer på R ⁿ

Man skulle kunna definiera många normer på vektorrummet R ⁿ . Några vanliga exempel är

• p -normen , definierad av ${\textstyle \|\mathbf {x} \|_{p}:={\sqrt[{p}]{\summa _{i=1}^{n}|x_{i}|^{p }}}}$ för alla $\mathbf {x} \in \mathbb {R} ^{n}$ där $p$ är ett positivt heltal. Fallet $p=2$ är mycket viktigt, eftersom det är exakt den euklidiska normen .
• ∞ $\infty$ -norm eller maxnorm , definierad av $=\max\{x_{1},\dots ,x_{n}\}}$$\|\mathbf {x} \|_{\infty$ för alla $\mathbf {x} \in \mathbb {R} ^{n}$ . Detta är gränsen för alla p-normer : ${\textstyle \|\mathbf {x} \|_{\infty }=\lim _{p\to \infty }{\sqrt[{p}]{\sum _{i=1}^{n }|x_{i}|^{p}}}}$ .

användbart resultat är att varje norm definierad på Rn ^. är ekvivalent Detta innebär att för två godtyckliga normer $\|\cdot \|$ och $\|\cdot \|'$ på R ⁿ kan du alltid hitta positiva reella tal ${ \displaystyle \alpha ,\beta >0}$ , så att

$$\alpha \cdot \|\mathbf {x} \|\leq \|\mathbf {x} \|'\cdot \beta \|\mathbf {x} \|$$

för alla $\mathbf {x} \in \mathbb {R} ^{n}$ .

Detta definierar en ekvivalensrelation på uppsättningen av alla normer på Rn ^. Med detta resultat kan du kontrollera att en sekvens av vektorer i R ⁿ konvergerar med $\|\cdot \|$ om och bara om den konvergerar med $\|\cdot \|'$ .

Här är en skiss på hur ett bevis på detta resultat kan se ut:

På grund av ekvivalensrelationen är det tillräckligt att visa att varje norm på R ⁿ är ekvivalent med den euklidiska normen $\|\cdot \|_{2}$ . Låt $\|\cdot \|$ vara en godtycklig norm på R ⁿ . Beviset är uppdelat i två steg:

• Vi visar att det finns ett $\beta >0$ , så att $\|\mathbf {x} \|\leq \beta \cdot \|\ mathbf {x} \|_{2}$ för alla $\mathbf {x} \in \mathbb {R} ^{n}$ . I det här steget använder du det faktum att varje $\mathbf {x} =(x_{1},\dots ,x_{n})\i \mathbb {R} ^{n}$ kan representeras som en linjär kombination av standardbasen : x $\textstyle \mathbf {x} =\summa _{i=1}^ {n}e_{i}\cdot x_{i}}$ . Sedan med Cauchy–Schwarz-ojämlikheten
  $$\|\mathbf {x} \|=\left\|\sum _{i=1}^{n}e_{i}\cdot x_{i}\right \|\leq \sum _{i=1}^{n}\|e_{i}\|\cdot |x_{i}|\leq {\sqrt {\sum _{i=1}^{n} \|e_{i}\|^{2}}}\cdot {\sqrt {\sum _{i=1}^{n}|x_{i}|^{2}}}=\beta \cdot \ |\mathbf {x} \|_{2},$$
  där ${\textstyle \beta :={\sqrt {\sum _{i=1}^{n}\|e_{i}\|^{2}} }}$ .
• Nu måste vi hitta ett $\alpha >0$ , så att $\alpha \cdot \|\mathbf {x} \|_{2}\ leq \|\mathbf {x} \|$ för alla $\mathbf {x} \in \mathbb {R} ^{n}$ . Antag att det inte finns någon sådan $\alpha$ . Då finns det för varje $k\in \mathbb {N}$ a $\mathbf {x} _{k}\in \mathbb {R} ^{n}$ , så att $\|\mathbf {x} _{k}\|_{2}>k\cdot \|\mathbf {x} _{k} \|$ . Definiera en andra sekvens $({\tilde {\mathbf {x} }}_{k})_{k\in \mathbb {N} }$ med ${\textstyle {\tilde {\mathbf {x} }}_{k}:={\frac {\mathbf {x} _{k}}{\|\mathbf {x} _ {k}\|_{2}}}}$ . Denna sekvens är begränsad eftersom $\|{\tilde {\mathbf {x} }}_{k}\|_{2}=1$ . Så på grund av Bolzano–Weierstrass-satsen finns det en konvergent undersekvens $({\tilde {\mathbf {x} }}_{k_{j}})_{j\in \mathbb {N} }$ med limit $\mathbf {a} \in$ R ⁿ . Nu visar vi att $\|\mathbf {a} \|_{2}=1$ men ${\displaystyle \mathbf {a} =\mathbf {0} } ,$ vilket är en motsägelse. Det är
  $$\$$
  eftersom $\|\mathbf {a} -{\tilde {\mathbf {x} }}_{k_{j}}\|\to 0$ och $0\leq {\frac {\|\mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_ {j}}\|_{2}}}<{\frac {1}{k_{j}}}$ , alltså ${\frac {\| \mathbf {x} _{k_{j}}\|}{\|\mathbf {x} _{k_{j}}\|_{2}}}\till 0$ . Detta innebär $\|\mathbf {a} \|=0$ , så $\mathbf {a} =\mathbf {0}$ . Å andra sidan $\|\mathbf {a} \|_{2}=1$ , eftersom $\|\mathbf {a} \|_{2}=\left\|\lim _{j\to \infty }{\tilde {\mathbf {x } }}_{k_{j}}\right\|_{2}=\lim _{j\to \infty }\left\|{\tilde {\mathbf {x} }}_{k_{j} }\right\|_{2}=1$ . Detta kan aldrig vara sant, så antagandet var falskt och det finns en sådan $\alpha >0$ .

Se även

• Exponential object , för teoretisk förklaring av den upphöjda notationen
• Geometriskt utrymme
• Verkligt projektivt utrymme

Fotnoter

•   Kelley, John L. (1975). Allmän topologi . Springer-Verlag. ISBN 0-387-90125-6 .
•   Munkres, James (1999). Topologi . Prentice-Hall. ISBN 0-13-181629-2 .