Polygram (geometri)
I geometri kan en generaliserad polygon kallas ett polygram och namnges specifikt av dess antal sidor. Alla polygoner är polygram, men kan också inkludera frånkopplade uppsättningar av kanter, som kallas en sammansatt polygon . Till exempel har ett vanligt pentagram , {5/2}, 5 sidor och det vanliga hexagrammet , {6/2} eller 2{3}, har 6 sidor uppdelade i två trianglar.
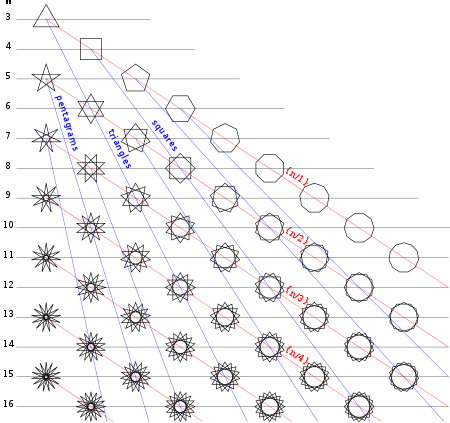
Ett regelbundet polygram { p / q } kan antingen vara i en uppsättning vanliga stjärnpolygoner (för gcd ( p , q ) = 1, q > 1) eller i en uppsättning regelbundna polygoner (om gcd( p , q ) > 1).
Etymologi
Polygramnamnen kombinerar ett numeriskt prefix , såsom penta- , med det grekiska suffixet -gram (som i detta fall genererar ordet pentagram ). Prefixet är normalt en grekisk kardinal , men synonymer som använder andra prefix finns. Suffixet -gram kommer från γραμμῆς ( grammos ) som betyder en linje.
Generaliserade regelbundna polygoner
Ett vanligt polygram, som en allmän regelbunden polygon , betecknas med dess Schläfli-symbol { p / q }, där p och q är relativt primtal (de delar inga faktorer) och q ≥ 2. För heltal p och q kan det övervägas som konstruerad genom att ansluta var q: te punkt av p -punkter som är regelbundet fördelade i en cirkulär placering.
 {5/2} |
 {7/2} |
 {7/3} |
 {8/3} |
 {9/2} |
 {9/4} |
 {10/3} ... |
Regelbundna sammansatta polygoner
I andra fall där n och m har en gemensam faktor tolkas ett polygram som en lägre polygon, { n / k , m / k }, med k = gcd( n , m ), och roterade kopior kombineras som en sammansatt polygon . Dessa figurer kallas vanliga sammansatta polygoner .
| Trianglar... | Rutor... | Pentagoner... | Pentagram... | ||||
|---|---|---|---|---|---|---|---|
.svg) {6/2}= 2{3} |
.svg) {9/3}= 3{3} |
.svg) {12/4}= 4{3} |
.svg) {8/2}= 2{4} |
.svg) {12/3}= 3{4} |
.svg) {10/2}= 2{5} |
.svg) {10/4}= 2{5/2} |
.svg) {15/6}= 3{5/2} |
Se även
- Cromwell, P.; Polyhedra , CUP, Hbk. 1997, ISBN 0-521-66432-2 . Pbk. (1999), ISBN 0-521-66405-5 . sid. 175
- Grünbaum, B. och GC Shephard; Tilings and Patterns , New York: WH Freeman & Co., (1987), ISBN 0-7167-1193-1 .
- Grünbaum, B.; Polyhedra with Hollow Faces, Proc of NATO-ASI Conference on Polytopes ... etc. (Toronto 1993) , ed T. Bisztriczky et al., Kluwer Academic (1994) s. 43–70.
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Kapitel 26. s. 404: Regular star-polytopes Dimension 2)
- Robert Lachlan, en elementär avhandling om modern ren geometri . London: Macmillan, 1893, sid. 83 polygram. [1]
- Branko Grünbaum , Metamorphoses of polygons , publicerad i The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, ( 1994)