Injektiv objekt

Inom matematiken , särskilt inom kategoriteorin , är begreppet injektivt objekt en generalisering av begreppet injektiv modul . Detta begrepp är viktigt inom kohomologi , i homotopileori och i teorin om modellkategorier . Den dubbla föreställningen är ett projektivt objekt .

Definition

Ett objekt Q är injektivt om, givet en monomorfism f : X → Y , vilket g : X → Q som helst kan utökas till Y .

Ett objekt $Q$ i en kategori $\mathbf {C}$ sägs vara injektivt om för varje monomorfism $f:X\to Y$ och varje morfism $g:X\to Q$ det finns en morfism $h:Y\to Q$ som förlänger $g$ till $Y$ , dvs. $h\circ f=g$ .

Det vill säga att varje morfism $X\to Q$ påverkar varje monomorfism $X\hookrightarrow Y$ .

Morfismen $h$ i definitionen ovan behöver inte vara unikt bestämd av $f$ och $g$ .

I en lokalt liten kategori motsvarar det att kräva att hom-funktionen $\operatorname {Hom} _{\mathbf {C} }(-,Q)$ bär monomorfismer i ${ \displaystyle \mathbf {C} }$ till surjektiva uppsättningskartor.

I Abeliska kategorier

Begreppet injektivitet formulerades först för abelska kategorier , och detta är fortfarande ett av dess primära tillämpningsområden. När $\mathbf {C}$ är en abelsk kategori, är ett objekt Q av $\mathbf {C}$ injektiv om och endast om dess hom-funktion Hom _C (–, Q ) är exakt .

Om $0\to Q\to U\to V\to 0$ är en exakt sekvens i $\mathbf {C}$ så att Q är injektiv, då delas sekvensen .

Tillräckligt med injektiver och injektiva skrov

Kategorin $\mathbf {C}$ sägs ha tillräckligt med injektiver om det för varje objekt X av $\mathbf {C}$ finns en monomorfism från X till ett injektivt objekt.

En monomorfism g i $\mathbf {C}$ kallas en essentiell monomorfism om för någon morfism f , den sammansatta fg är en monomorfism endast om f är en monomorfism.

Om g är en essentiell monomorfism med domän X och en injektiv kodomän G , så kallas G ett injektivt skrov av X. Det injektiva skrovet bestäms sedan unikt av X upp till en icke-kanonisk isomorfism.

Exempel

• I kategorin abelska grupper och grupphomomorfismer , Ab , är ett injektivt objekt nödvändigtvis en delbar grupp . Om man antar valets axiom är begreppen likvärdiga.
• I kategorin (vänster) moduler och modulhomomorfismer , R - Mod , är ett injektivt objekt en injektiv modul . R - Mod har injektiva skrov (som en konsekvens har R - Mod tillräckligt med injektiver).
• I kategorin metriska utrymmen, Met , är ett injektivt objekt ett injektivt metriskt utrymme , och det injektiva skrovet i ett metriskt utrymme är dess snäva spännvidd .
• I kategorin ₀ T- rum och kontinuerliga avbildningar är ett injektivt objekt alltid en Scott-topologi på ett kontinuerligt gitter , och därför är det alltid sobert och lokalt kompakt .

Används

Om en abelsk kategori har tillräckligt med injektiver kan vi bilda injektivupplösningar , dvs för ett givet objekt X kan vi bilda en lång exakt sekvens

$0\to X\to Q^{0}\to Q^{1}\to Q^{2}\to \cdots$

och man kan sedan definiera de härledda funktorerna för en given funktion F genom att applicera F på denna sekvens och beräkna homologin för den resulterande (inte nödvändigtvis exakta) sekvensen. Detta tillvägagångssätt används för att definiera Ext- och Tor- funktioner och även de olika kohomologiteorierna inom gruppteori , algebraisk topologi och algebraisk geometri . Kategorierna som används är typiskt funktionskategorier eller kategorier av skivor av O _X -moduler över något ringmärkt utrymme ( X , O _X ) eller, mer allmänt, någon Grothendieck-kategori .

Generalisering

Ett objekt Q är H -injektiv om, givet h : A → B i H , någon f : A → Q faktorer genom h .

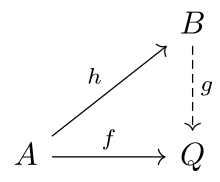
Låt $\mathbf {C}$ vara en kategori och låt ${\mathcal {H}}$ vara en klass av morfismer av $\mathbf {C}$ .

Ett objekt $Q$ av $\mathbf {C}$ sägs vara ${\mathcal {H}}$ -injektiv om för varje morfism $f :A\to Q$ och varje morfism $h:A\to B$ i ${\mathcal {H}}$ finns det en morfism $g :B\to Q$ med $g\circ h=f$ .

Om ${\mathcal {H}}$ är klassen av monomorfismer , är vi tillbaka till de injektiva objekten som behandlades ovan.

Kategorin $\mathbf {C}$ sägs ha tillräckligt med ${\mathcal {H}}$ -injektiver om det finns för varje objekt X av ${\displaystyle \mathbf {C} } .$ en ${\mathcal {H}}$ -morfism från X till ett ${\mathcal {H}}$ -injektivt objekt.

En ${\mathcal {H}}$ -morfism g i $\mathbf {C}$ kallas ${\displaystyle {\mathcal {H}}} -$ väsentlig om för någon morfism f , sammansatt fg är i ${\mathcal {H}}$ endast om f är i ${\mathcal {H}}$ .

Om g är en ${\mathcal {H}}$ -essentiell morfism med domän X och en ${\mathcal {H}}$ -injektiv koddomän G , då kallas G en ${\mathcal {H}}$ -injektiv skrov av X .

Exempel på H -injektiva objekt

• I kategorin för enkla uppsättningar är de injektiva objekten med avseende på klassen ${\mathcal {H}}$ av anodyna tillägg Kan-komplex .
• I kategorin partiellt ordnade uppsättningar och monotona kartor bildar de kompletta gittren de injektiva objekten för klassen ${\mathcal {H}}$ av orderinbäddningar , och Dedekind–MacNeilles komplettering av en partiellt ordnad uppsättning är dess ${\mathcal {H}}$ -injektiv skrov.

Se även

• Projektivt objekt

Anteckningar

• Jiri Adamek, Horst Herrlich, George Strecker. Abstrakta och konkreta kategorier: The joy of cats, Kapitel 9, Injective Objects and Essential Embeddings, Republished in Reprints and Applications of Categories, nr. 17 (2006) s. 1-507 , Wiley (1990).
• J. Rosicky, Injektivitet och tillgängliga kategorier
• ₀ F. Cagliari och S. Montovani, T -reflektion och injicerande skrov av fiberutrymmen