E 6 polytop
 2 21 |
 1 22 |
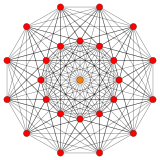
I 6-dimensionell geometri finns det 39 enhetliga polytoper med E 6 symmetri. De två enklaste formerna är 2 21 och 1 22 polytoper, sammansatta av 27 respektive 72 hörn .
De kan visualiseras som symmetriska ortografiska projektioner i Coxeter-plan av E 6 Coxeter-gruppen och andra undergrupper.
Grafer
Symmetriska ortografiska projektioner av dessa 39 polytoper kan göras i E 6 , D 5 , D 4 , D 2 , A 5 , A 4 , A 3 Coxeter plan . A k har k+1 symmetri, Dk har 2 (k-1) symmetri och E6 har 12 symmetri .
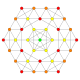
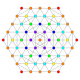
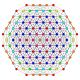
Grafer med sex symmetriplan visas för 9 av de 39 polytoperna i E 6 -symmetrin. Topparna och kanterna ritade med hörn färgade av antalet överlappande hörn i varje projektiv position.
| # | Coxeter plan grafer |
Coxeter diagram Namn |
|||||
|---|---|---|---|---|---|---|---|
|
Aut(E 6 ) [18/2] |
E 6 [12] |
D 5 [8] |
D 4 / A 2 [6] |
A 5 [6] |
D 3 / A 3 [4] |
||
| 1 |  |
 |
 |
 |
 |
 |
2 21 Icosihepta-heptacontidipeton (jak) |
| 2 | 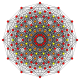 |
 |
 |
 |
 |
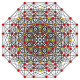
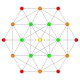
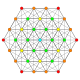
Rectified 2 21 Rectified icosihepta-heptacontidipeton (rojak) |
|
| 3 |  |
 |
 |
 |
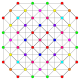 |
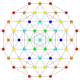
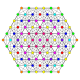
Trirectified 221 Trirectified icosihepta-heptacontidipeton (harjak) |
|
| 4 |  |
 |
 |
 |
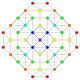 |
Trunkerad 2 21 Trunkerad icosihepta-heptacontidipeton (tojak) |
|
| 5 |  |
 |
 |
 |
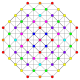 |
Kantellerad 2 21 Kantellerad icosihepta-heptacontidipeton |
|
| # | Coxeter plan grafer |
Coxeter diagram Namn |
||||||
|---|---|---|---|---|---|---|---|---|
|
Aut(E 6 ) [18] |
E 6 [12] |
D 5 [8] |
D 4 / A 2 [6] |
A 5 [6] |
D 6 / A 4 [10] |
D 3 / A 3 [4] |
||
| 6 | 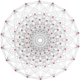 |
 |
 |
 |
 |
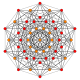 |
 |
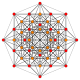
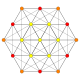
1 22 Pentacontatetrapeton (mån) |
| 7 |  |
 |
 |
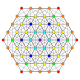 |
 |
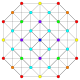 |
Rectified 1 22 / Birectified 2 21 Rectified pentacontatetrapeton (ram) |
|
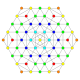
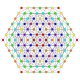
| 8 | 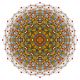 |
 |
 |
 |
 |
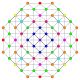 |
Birectified 1 22 Birectified pentacontatetrapeton (barm) |
|
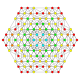
| 9 |  |
 |
 |
 |
 |
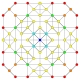 |
Trunkerad 1 22 Trunkerad pentacontatetrapeton (tim) |
|
-
HSM Coxeter :
- HSM Coxeter, Regular Polytopes , 3:e upplagan, Dover New York, 1973
-
Kaleidoscopes: Selected Writings of HSM Coxeter , redigerad av F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Wiley::Kaleidoscopes: Selected Skrifter av HSM Coxeter
- (Papper 22) HSM Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Papper 23) HSM Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
- (Papper 24) HSM Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45]
- NW Johnson : Theory of Uniform Polytopes and Honeycombs , Ph.D. Avhandling, University of Toronto, 1966
- Klitzing, Richard. "6D enhetliga polytoper (polypeta)" .
Kategori: