Dupin cyklid

En Dupin-cykel

Inom matematiken är en Dupin-cyklid eller cyklid av Dupin vilken geometrisk inversion som helst av en standardtorus , cylinder eller dubbelkon . I synnerhet är dessa senare själva exempel på Dupin-cyklider. De upptäcktes av (och uppkallades efter) Charles Dupin i hans avhandling från 1803 under Gaspard Monge . Den viktigaste egenskapen hos en Dupin-cyklid är att den är en kanalyta (hölje av en enparameterfamilj av sfärer) på två olika sätt. Denna egenskap betyder att Dupin-cyklider är naturliga objekt i Lie-sfärens geometri .

Dupin-cyklider är ofta helt enkelt kända som cyklider , men den senare termen används också för att hänvisa till en mer allmän klass av kvartsytor som är viktiga i teorin om separation av variabler för Laplace-ekvationen i tre dimensioner.

Dupin-cyklider undersöktes inte bara av Dupin utan också av A. Cayley , JC Maxwell och Mabel M. Young .

Dupin-cyklider används i datorstödd design eftersom cyklidplåster har rationella representationer och är lämpliga för att blanda kanalytor (cylinder, koner, tori och andra).

Definitioner och egenskaper

Det finns flera likvärdiga definitioner av Dupin-cyklider. I $\mathbb {R} ^{3}$ kan de definieras som bilderna under valfri inversion av tori, cylindrar och dubbla koner. Detta visar att klassen av Dupin-cyklider är invariant under Möbius (eller konforma) transformationer . I det komplexa utrymmet $\mathbb {C} ^{3}$ kan dessa tre senare varianter mappas till varandra genom inversion, så Dupin-cyklider kan definieras som inversioner av torus (eller cylindern eller den dubbla kon).

Eftersom en standardtorus är omloppsbanan för en punkt under en tvådimensionell abelisk undergrupp av Möbiusgruppen, följer det att cykliderna också är det, och detta ger ett andra sätt att definiera dem.

En tredje egenskap som kännetecknar Dupin-cyklider är att deras krökningslinjer är alla cirklar (möjligen genom punkten i oändligheten) . På motsvarande sätt är krökningssfärerna, som är de sfärer som tangerar ytan med radier lika med reciproka av de huvudsakliga krökningarna vid tangentpunkten, konstanta längs motsvarande krökningslinjer: de är tangentsfärerna som innehåller motsvarande krökningslinjer som stora cirklar . Återigen på motsvarande sätt degenererar båda arken av fokalytan till koner. Det följer att vilken Dupin-cyklid som helst är en kanalyta (dvs höljet av en enparameterfamilj av sfärer) på två olika sätt, och detta ger en annan karaktärisering.

Definitionen i termer av sfärer visar att klassen av Dupin-cyklider är invariant under den större gruppen av alla Lie-sfäromvandlingar ; vilka två Dupin-cykler som helst är Lie-ekvivalenta . De bildar (i någon mening) den enklaste klassen av Lie-invarianta ytor efter sfärerna, och är därför särskilt betydelsefulla i Lie-sfärgeometrin .

Definitionen betyder också att en Dupin-cyklid är enveloppen för en-parameterfamiljen av sfärer som tangerar tre givna ömsesidigt tangentiella sfärer. Det följer att det tangerar oändligt många Soddys hexlet -konfigurationer av sfärer.

Parametrisk och implicit representation

(CS): En Dupin-cyklid kan representeras på två sätt som enveloppen av en enparametrisk penna av sfärer, dvs det är en kanalyta med två riktlinjer . Direktrissparet är fokala koniska och består antingen av en ellips och en hyperbel eller av två paraboler. I det första fallet definierar man cykliden som elliptisk , i det andra fallet som parabolisk . I båda fallen är konikerna inneslutna i två ömsesidigt ortogonala plan. I extrema fall (om ellipsen är en cirkel) urartar hyperbeln till en linje och cykliden är en rotationstorus.

En ytterligare speciell egenskap hos en cykel är:

(CL): Varje krökningslinje för en Dupin-cyklid är en cirkel .

Elliptiska cyklider

En elliptisk cyklid kan representeras parametriskt med följande formler (se avsnittet Cyklid som kanalyta ):

Betydelsen av designparametrarna $a,b,c,d$ : $d$ är radien för den genererande sfären vid ellipsens co-vertex De två cirklarna i xz-plan med mittpunkter $(\pm a,0,0)$ har radier $d\mp c$ . Här: $a=1,\;b=0,98\to c=0,199$ och $d=0,3$

$x={\frac {d(ca\cos u\cos v)+ b^{2}\cos u}{ac\cos u\cos v}}\ ,$

$y ={\frac {b\sin u(ad\cos v)}{ac\cos u\cos v}}\ ,$

$z={\frac {b\sin v(c\cos ud)}{ac\cos u\cos v}}\ ,$

$0\leq u,v<2\pi \ .$

Siffrorna $a,b,c,d$ är semi-dur och semi-mollaxlar och $c$ ellipsens linjära excentricitet:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1,z=0\ .$

Hyperbeln ${\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b ^{2}}}=1,y=0$ är fokalkonen till ellipsen. Det betyder: Ellipsens brännpunkter/punktpunkter är hyperbelns hörn/härdar. De två koniska formerna bildar de två degenererade fokalytorna av cykliden.

$d$ kan betraktas som medelradien för de genererande sfärerna.

För $u=const$ , $v=const$ respektive får man ytans krökningslinjer (cirklar).

Den motsvarande implicita representationen är:

$(x^{2}+y^{2}+z^{2}+b^{2}-d^{2})^{2}-4(ax-cd)^{2}- 4b^{2}y^{2}=0\ .$

I fallet med $a=b$ får man $c=0$ , dvs ellipsen är en cirkel och hyperbeln degenererar till en linje. Motsvarande cyklider är tori av revolution.

(ellipt.) Dupin-cyklider för designparametrar a,b,c,d
$d=0$	$0<d<c$	$d=c$	$c<d$	$d=a$	$a<d$
symm. horncykel	horncykel	horncykel	ringcykel	ringcykel	spindelcykel

Mer intuitiva designparametrar är skärningspunkterna mellan cykliden och x-axeln. Se avsnittet Cykla genom 4 punkter på x-axeln .

Paraboliska cyklider

En parabolisk cyklid kan representeras av följande parametriska representation (se avsnittet Cyklid som kanalyta ):

parabolisk cyklid med dess direktriser (fokala paraboler)

$x={\frac {p}{2}}\,{\frac {2v^{ 2}+k(1-u^{2}-v^{2})}{1+u^{2}+v^{2}}}\ ,$

$y=pu\,{\frac {v^{2}+k}{1+u^{2}+v^{2}}}\ ,$

$z=pv\,{\frac {1+u^{2}-k}{1+u^{2}+v^{2}}} \ ,$

$-\infty <u,v<\infty \ .$

Talet $p$ bestämmer formen på båda parabolerna, som är fokala koniska:

$y^{2}=p^{2}-2px,\ z=0\$ och $\ z^{2}=2px,\ y=0\ .$

$k$ bestämmer förhållandet mellan diametrarna för de två hålen (se diagram). $k=0,5$ betyder: båda diametrarna är lika. För diagrammet är $k=0,7$ .

En motsvarande implicit representation är

$\left(x+\left({\frac {k}{2}}-1\right)p\right)\left(x^{2}+y^{2}+z^{2}- {\frac {k^{2}p^{2}}{4}}\right)+pz^{2}=0\ .$

paraboliska Dupin-cyklider för designparametrar p=1, k
$k=0,5$	$k=1$	$k=1,5$
ringcykel	horncykel	horncykel

Anmärkning : Genom att visa cirklarna uppstår luckor som orsakas av nödvändig begränsning av parametrarna $u,v$ .

Cyklid som kanalyta

Dupin-cyklid som kanalyta ( hölje av en familj av sfärer)

Det finns två sätt att generera en elliptisk Dupin-cyklid som en kanalyta . Den första använder en ellips som riktlinje, den andra en hyperbel:

Ellips som regissör

I xy-planet är riktningen ellipsen med ekvation

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{ 2}}}=1\ ,\ z=0\quad$ och $\ a>b$ .

Den har den parametriska representationen

$\ x=a\cos \varphi \;,\ y=b\sin \varphi \;,\ z=0\ .$

$a$ är semi-dur och $b$ semi-mollaxeln. $c$ är ellipsens linjära excentricitet. Därför: $c^{2}=a^{2}-b^{2}$ . Radierna för de genererande sfärerna är

$r(\varphi )=dc\cos \varphi \ .$

$d$ är en designparameter. Det kan ses som medelvärdet av sfärernas radier. I fallet med $c=0$ är ellipsen en cirkel och cykliden en rotationstorus med $d$ radien för den genererande cirkeln (generatris).

I diagrammet: $\;a=1,\;b=0,99,\ d=0,25\;$ .

Maxwell: Egenskapen för direktrixellipsens foci. Ellipsen är en uppsättning av de blå och lila cirklarna på samma avstånd.

Maxwell egendom

Följande enkla relation mellan det faktiska sfärcentrumet (ellipspunkten) och motsvarande sfärradie beror på Maxwell:

• Skillnaden/summan av sfärens radie och avståndet för sfärens centrum (ellipspunkt) från en (men fast) av brännpunkterna är konstant.

Bevis

Ellipsens brännpunkter $\ E=(a\cos \varphi ,b\sin \varphi ,0)\$ är $\ F_{i}=(\pm c,0,0)\$ . Om man väljer $\ F_{1}=(c,0,0)\$ och beräknar avståndet $\ |EF_{1}|\$ , man får $\ |EF_{1}|=ac\cos \varphi \$ . Tillsammans med radien för den faktiska sfären (se ovan) får man $\ |EF_{1}|-r=ad\$ . Att välja det andra fokuset ger: $\ |EF_{2}|+r=a+d\ .$

Därav:

I xy-planet är höljena av sfärernas cirklar två cirklar med ellipsens foci som centrum och radierna $a\pm d$ (se diagram).

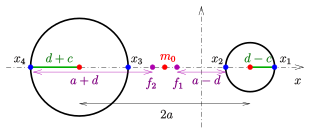
Cykla genom 4 punkter på x-axeln

Bestämma designparametrarna a,b,c,d som hör till de givna realerna $x_{1},x_{2},x_{3},x_{4}$

topp: ringcykel med $x_{1}=3,x_{2}=1,x_{3}=-3 ,x_{4}=-7$ mitten: horncykel med $x_{1}=1,x_{2}= 3,x_{3}=-3,x_{4}=-7$ botten: spindelcykel med $x_{1 }=3,x_{2}=-3,x_{3}=1,x_{4}=-7$

Maxwell-egenskapen ger anledning till att bestämma en ringcyklid genom att föreskriva dess skärningspunkter med x-axeln:

Givet: Fyra punkter $x_{1}>x_{2}>x_{3}>x_{4}$ på x-axeln (se diagram).

Önskas: Center $m_{0}$ , halvaxlar $a,b$ , linjär excentricitet $c$ och foci för direktrixellipsen och parametern $d$ för motsvarande ringcyklid.

Från Maxwell-egendomen härrör man

$2(a+d)=x_{1}-x_{4}\;,\quad \ 2(ad)=x_{2}-x_{3}\ .$

Lösning för $a,c$ ger

$a={\frac {1}{4}}\left(x_{1}+x_{2}-x_{3} -x_{4}\right),\quad$$d={\frac {1}{4}}\left(x_{1}-x_{2}+x_{3}-x_{4}\right)\ .$

Foci (på x-axeln) är

$f_{1}={\frac {1}{2}}(x_{2}+x_ {3}),\quad f_{2}={\frac {1}{2}}(x_{1}+x_{4})$ och därmed

$c={\frac {1}{4}}\left(-x_{1}+x_{2}+x_{3}-x_{4} \right)\;,\quad \ b={\sqrt {a^{2}-c^{2}}}\$

Mitten av de fokala konerna (ellips och hyperbel) har x-koordinaten

$m_{0}={\frac {1}{4}}\left(x_{1}+x_{2}+x_{3}+x_{4}\right)\ .$

Om man vill visa cykliden med hjälp av den parametriska representationen ovan måste man överväga skiftet $m_{0}$ i mitten!

Betydelsen av ordningen på talen $x_{1},x_{2},x_{3},x_{4}$

(Beräkningen ovan förutsätter $x_{1}>x_{2}>x_{3}>x_{4}$ , se diagram.)

(H) Att byta $x_{1},x_{2}$ genererar en horncyklid. (S) Att byta $x_{2},x_{3}$ genererar en spindelcykel. (H1) För $x_{1}=x_{2}=2$ får man en 1-hornscykel. (R) För $x_{2}=x_{3}=0$ får man en ringcykel som rör sig vid utgångspunkten.

Parallella ytor

Parallella ytor av en ringcyklid med parametrarna $a=1,b=0,98,\ d=0,30,0,45,0,60$

Genom att öka eller minska parameter $d$ , så att typen inte ändras, får man parallella ytor (liknar parallella kurvor ) av samma typ (se diagram).

Hyperbel som riktlinje

Det andra sättet att generera ringcykliden som kanalyta använder den fokala hyperbeln som riktlinje. Den har ekvationen

Cyklid med två berörande sfärer med centrum på direktrixhyperbolen

${\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1\ ,\ y=0\ .$

I detta fall berör sfärerna cykliden utifrån vid den andra familjen av cirklar (krökningslinjer). Till varje arm av hyperbeln hör en underfamilj av cirklar. En familjs sfärer omsluter cykliden (i diagrammet: lila). Den andra familjens sfärer berörs utifrån av cykliden (blå).

Parametrisk representation av hyperbeln:

$(\pm c\cosh \psi ,0,b\sinh \psi )\ .$

Radierna för motsvarande sfärer är

$R(\psi )=a\cosh \psi \mp d\ .$

I fallet med en torus ( $c=0$ ) degenererar hyperbeln till torusaxeln.

Maxwell-egenskap för hyperbelfallet. Hyperbelarmen $H_{+}$ är en kurva på samma avstånd för båda de grå cirklarna.

Maxwell-property (hyperbolfall)

Fokus för hyperbeln $\;H_{\pm }(\psi )=(\pm c\cosh \psi ,0, b\sinh \psi )\;$ är $\;F_{i}=(\pm a,0,0)\;$ . Avståndet för hyperbelpunkten $\;H_{+}(\psi )=(c\cosh \psi ,0,b\sinh \ psi )\;$ till fokus $F_{1}$ är $\;|H_{+}F_{1}|=a\cosh \psi -c\;$ och tillsammans med sfärens radie $R_{+}(\psi )=a\cosh \psi -d$ man får $\;|H_{+}F_{1}|-R_{+}=dc\;$ . Analogt får man $\;|H_{+}F_{2}|-R_{+}=d+c\;$ . För en punkt på hyperbelns andra arm härleder man ekvationerna: $\;R_{-}-|H_{-}F_{1}|=dc\;,\ R_{-}-|H_{-}F_{2}|=d+c\;.$

Därav:

I xz-planet cirklarna för sfärerna med centrum $H_{\pm }(\psi )$ och radier $R_{\pm }(\psi )$ har de två cirklarna (i diagrammet grå) med mittpunkter $F_{1/2}=(\pm a,0,0)$ och radien $d\mp c$ som kuvert.

Punktkonstruktion

Härledning av den parametriska representationen

Elliptisk cyklid

Ellipsen och hyperbeln (fokala koner) är de degenererade fokalytorna av den elliptiska cykliden. För alla par $E,H$ av punkter i ellipsen och hyperbeln gäller följande (på grund av definitionen av en fokal yta):

1) Linjen ${\overline {EH}}$ är en normal för cykeln och

2) motsvarande punkt $P$ för cykeln delar ackordet $EH$ med relation $r:R$ (se diagram).

Från den parametriska representationen av fokalkonikerna och sfärernas radier

Ellips: $\quad \ \ \ E(u)=(a\cos u ,b\sin u,0),\quad r(u)=dc\cos u\ \ ,$

Hyperbel: $\quad H(v)=({\frac {c}{\cos v}},0,b\tan v),\quad R(u)={\frac {a}{\cos v} }-d\ .$

man får motsvarande punkt $P$ för cykeln (se diagram):

$\ P(u,v)={\frac {R(v)}{r(u)+R(v)}}\;E(u)+{\frac {r(u)}{r (u)+R(v)}}\;H(v)\ .$

(För den ovanliga men bekväma parametriska representationen av hyperbeln: se hyperbel .)

Beräkning i detalj leder till den parametriska representationen av den elliptiska cykliden som ges ovan .

Om man använder den parametriska representationen som ges i artikeln om kanalytor, så består i allmänhet bara en familj av parametriska kurvor av cirklar.

Parabolisk cyklid

Generering av en parabolisk cyklid som kanalyta

Härledningen av den parametriska representationen för det paraboliska fallet går analogt:

Med de parametriska representationerna av fokalparabolerna (degenererade fokalytor) och sfärernas radier:

$P_{1}(u)=\left({\ frac {p}{2}}(1-u^{2}),pu,0\right),\quad r_{1}={\frac {p}{2}}(1-k+u^{ 2})\;$

$P_{2}(v)=\left({\ frac {p}{2}}v^{2},0,pv\right),\qquad \qquad r_{2}={\frac {p}{2}}(k+v^{2})\$

man får

$\ P(u,v)={\frac {r_{2}(v)}{r_{1}(u)+r_{2}(v)}}\;P_{1}(u) +{\frac {r_{1}(u)}{r_{1}(u)+r_{2}(v)}}\;P_{2}(v)$

som ger den parametriska representationen ovan av en parabolisk cyklid.

Dupin-cyklider och geometriska inversioner

En fördel för undersökningar av cyklider är egenskapen:

(I): Vilken Dupin-cyklid som helst är bilden av antingen en rät cirkulär cylinder eller en rät cirkulär dubbelkon eller en rotationstorus genom en inversion (reflektion vid en sfär).

Inversionen vid sfären med ekvation $x^{2}+y^{2}+z^{2}=R^{2}$ kan beskrivas analytiskt med :

$(x,y,z)\högerpil {\frac {R^{2}\cdot (x,y,z)}{x^{2}+y^{2}+z^{2}} }\ .$

De viktigaste egenskaperna hos en inversion vid en sfär är:

1. Sfärer och cirklar mappas på samma objekt.
2. Plan och linjer som innehåller ursprunget (inversionscentrum) kartläggs på sig själva.
3. Plan och linjer som inte innehåller origo mappas på sfärer eller cirklar som passerar origo.
4. En inversion är ofrivillig (identisk med den inversa mappningen).
5. En inversion bevarar vinklar.

Man kan kartlägga godtyckliga ytor genom en inversion. Formlerna ovan ger i alla fall parametriska eller implicita representationer av bildytan, om ytorna är givna parametriskt eller implicit. Vid en parametrisk yta får man:

$(x(u,v),y(u,v),z(u,v))\högerpil {\frac {R^{2}\cdot (x(u,v),y(u, v),z(u,v))}{x(u,v)^{2}+y(u,v)^{2}+z(u,v)^{2}}}\ .$

ringcyklid genererad av en inversion av en cylinder vid en sfär (magenta)

parabolisk ringcyklid genererad av en inversion av en cylinder som innehåller ursprunget

horncyklid genererad av en inversion av en kon

ringcyklid genererad av en inversion av en torus

Men: Endast vid rätt cirkulära cylindrar och koner och rotationstorier får man Dupin-cyklider och vice versa.

Exempel cylinder

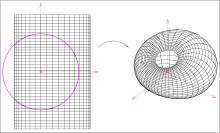
a) Eftersom linjer, som inte innehåller origo, kartläggs av en inversion vid en sfär (i bild: magenta) på cirklar som innehåller origo, är bilden av cylindern en ringcyklid med ömsesidigt berörande cirklar i origo. Eftersom bilderna av linjesegmenten, som visas i bilden, visas cirkelsegment på linjen som bilder. Sfärerna som berör cylindern på insidan kartläggs på en första penna av sfärer som genererar cykliden som en kanalyta. Bilderna av cylinderns tangentplan blir den andra pennan av sfärer som berör cykliden. De senare passerar genom ursprunget. b) Det andra exemplet inverserar en cylinder som innehåller origo. Linjer som passerar origo mappas på sig själva. Därför är ytan obegränsad och en parabolisk cyklid.

Exempel kon

Linjerna som genererar konen är avbildade på cirklar, som skär varandra vid origo och bilden av konens vertex. Bilden av konen är en dubbelhornscyklid. Bilden visar bilderna av linjesegmenten (av konen), som faktiskt är cirkelsegment.

Exempel torus

Båda cirklarpennorna på torusen (visas på bilden) är avbildade på motsvarande cirklarpennor på cykliden. I händelse av en självkorsande torus skulle man få en spindelcykel.

Villarceau cirklar

Ringcykel med Villarceau-cirklar

Eftersom Dupin-ringcyklider kan ses som bilder av tori via lämpliga inversioner och en inversion kartlägger en cirkel på en cirkel eller linje, bildar bilderna av Villarceau- cirklarna ytterligare två familjer av cirklar på en cyklid (se diagram).

Bestämma designparametrarna $a,b,c,d$

Formeln för inversionen av en parametrisk yta (se ovan) ger en parametrisk representation av en cyklid (som inversion av en torus) med cirklar som parametriska kurvor. Men poängen i ett parametriskt nät är inte väl fördelade. Så det är bättre att beräkna designparametrarna $a,b,c,d$ och att använda den parametriska representationen ovan:

Cyklid (blå) som bild genom en inversion av en torus (svart) vid enhetssfären (röd)

Givet: En torus, som förskjuts från standardpositionen längs x-axeln. Låt vara $x_{1},x_{2},x_{3},x_{4}$ skärningspunkterna mellan torus och x-axeln (se diagram) . Alla inte noll. Annars skulle inversionen av torus inte vara en ringcyklid. Önskas: halvaxlar $a,b$ och linjär excentricitet $c$ för ellipsen (directrix) och parameter $d$ för ringcykliden, som är bilden av torus under inversionen vid enhetssfären.

Inversionen mappar $x_{i}$ till ${\displaystyle {\tfrac {1}{x_{i}}}} ,$ som är x-koordinaterna för 4 punkter i ringcykliden ( se diagram). Från sektionen Cykla genom 4 punkter på x-axeln får man

$a={\frac {1}{4}}\left({\frac {1}{x_{1 }}}+{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}-{\frac {1}{x_{4}}}\right),\ quad$$d={\frac {1}{4}}\left(-{\frac {1}{ x_{1}}}+{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right )\$ och

$c={\frac {1}{4}}\left ({\frac {1}{x_{1}}}-{\frac {1}{x_{2}}}-{\frac {1}{x_{3}}}+{\frac {1}{ x_{4}}}\right)\;,\quad \ b={\sqrt {a^{2}-c^{2}}}\$

Mitten av fokalkonikerna har x-kordinaten

$m_{0}={\frac {1}{4}}\left({\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+{ \frac {1}{x_{3}}}+{\frac {1}{x_{4}}}\right)\ .$

Separation av variabler

Dupin-cyklider är ett specialfall av ett mer allmänt begrepp om en cyklid, vilket är en naturlig förlängning av begreppet en quadric yta . Medan en kvadric kan beskrivas som nollmängden av andra ordningens polynom i kartesiska koordinater ( x ₁ , x ₂ , x ₃ ), ges en cyklid av nollmängden av ett andra ordningens polynom i ( x ₁ , x ₂ , x ₃ , r2 ) ^, där r2 = x ₁ ² + x ₂ ² + x ₃ ^{2 .} Det är alltså en kvartsyta i kartesiska koordinater, med en ekvation av formen:

$Ar^{4 }+\summa _{i=1}^{3}P_{i}x_{i}r^{2}+\summa _{i,j=1}^{3}Q_{ij}x_{i} x_{j}+\summa _{i=1}^{3}R_{i}x_{i}+B=0$

där Q är en 3x3 matris, P och R är 3-dimensionella vektorer och A och B är konstanter.

Familjer av cyklider ger upphov till olika cyklidiska koordinatgeometrier.

I Maxime Bôchers avhandling från 1891, Ueber die Reihenentwickelungen der Potentialtheorie , visades att Laplace-ekvationen i tre variabler kan lösas med hjälp av separation av variabler i 17 konformt distinkta kvadriska och cyklidiska koordinatgeometrier. Många andra cyklidiska geometrier kan erhållas genom att studera R-separation av variabler för Laplace-ekvationen.

Se även

• Inversion av kurvor och ytor (tyska)

externa länkar

• Dupin cykler på MathCurve

Anteckningar

•   Cecil, Thomas E. (1992), Lie sphere geometri , New York: Universitext, Springer-Verlag, ISBN 978-0-387-97747-8 .
• Eisenhart, Luther P. (1960), "§133 Cyclides of Dupin", A Treatise on the Differential Geometry of Curves and Surfaces , New York: Dover, s. 312–314 .
•   Hilbert, David ; Cohn-Vossen, Stephan (1999), Geometry and the Imagination , American Mathematical Society, ISBN 0-8218-1998-4 .
•   Moon, Parry; Spencer, Domina Eberle (1961), Fältteorihandbok: inklusive koordinatsystem, differentialekvationer och deras lösningar , Springer, ISBN 0-387-02732-7 .
• O'Connor, John J.; Robertson, Edmund F. (2000), "Pierre Charles François Dupin" , MacTutor History of Mathematics arkiv .
• Pinkall, Ulrich (1986), "§3.3 Cyclides of Dupin", i G. Fischer (red.), Mathematical Models from the Collections of Universities and Museums , Braunschweig, Tyskland: Vieweg, s. 28–30 .
• Miller, Willard (1977), Symmetry and Separation of Variables .
• A. Cayley (1873) "On the cyclide", Quarterly Journal of Pure and Applied Mathematics 12: sid. 148–163.
• V. Chandru, D. Dutta, CM Hoffmann (1989) "On the geometri of Dupin cyclides", The Visual Computer. (5), sid. 277–290.
• C. Dupin (1822) Applications de Geometrie et de Mechanique. Bachelier, Paris.
•   F. Klein, W. Blaschke (1926) Vorlesungen Über Höhere Geometrie. Springer-Verlag, ISBN 978-3-642-98494-5 , sid. 56.
• JC Maxwell (1868) "On the cyclide", Quarterly Journal of Pure and Applied Mathematics 9: sid. 111–126.
•   MJ Pratt (1989) Cyclide Blending in Solid Modelling. I: Wolfgang Strasser, Hans-Peter Seidel (Hrsg.): Theory and Practice in Geometric Modelling. Springer-Verlag, ISBN 0-387-51472-4 , sid. 235.
• YL Srinivas, V. Kumar, D. Dutta (1996) "Surface design using cyclide patches", Computer-Aided Design 28(4): 263–276.
• Mabel M. Young (1916) "Dupin's cyclide as a self-dual surface", American Journal of Mathematics 38(3): 269–286

externa länkar

• Weisstein, Eric W. "Cyclide" . MathWorld .
• E. Berberich, M. Kerber: Arrangemang på ytor av Genus One: Tori och Dupin cyklider.