Parallell kurva

Ej att förväxla med parallell transport .

Parallella kurvor för grafen för $y=1,5\sin(x)$ för avstånd $d=0,25,\dots ,1,5$

Två definitioner av en parallell kurva: 1) envelopp av en familj av kongruenta cirklar, 2) med ett fast normalavstånd

De parallella kurvorna för en cirkel (röd) är också cirklar

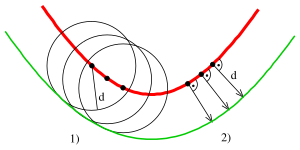
En parallell av en kurva är enveloppen av en familj av kongruenta cirklar centrerade på kurvan. Det generaliserar begreppet parallella (raka) linjer . Det kan också definieras som en kurva vars punkter ligger på ett konstant normalt avstånd från en given kurva. Dessa två definitioner är inte helt likvärdiga eftersom den senare förutsätter jämnhet , medan den förra inte gör det.

I datorstödd design är den föredragna termen för en parallellkurva offsetkurva . (I andra geometriska sammanhang termen offset också syfta på translation .) Offsetkurvor är viktiga till exempel vid numeriskt styrd bearbetning , där de beskriver till exempel formen på snittet som görs av ett runt skärverktyg i en tvåaxlig maskin. Formen på skäret är förskjutet från skärarens bana med ett konstant avstånd i riktningen vinkelrätt mot skärbanan vid varje punkt.

Inom området för 2D- datorgrafik , känd som vektorgrafik , är den (ungefärliga) beräkningen av parallella kurvor involverad i en av de grundläggande ritoperationerna, som kallas strykning, som vanligtvis tillämpas på polylinjer eller polybeziers (som i sig själva kallas banor) i det fältet.

Förutom i fallet med en linje eller cirkel har de parallella kurvorna en mer komplicerad matematisk struktur än stamfaderkurvan. Till exempel, även om progenitorkurvan är jämn , kanske dess förskjutningar inte är det; denna egenskap illustreras i den översta figuren, med en sinuskurva som progenitorkurva. I allmänhet, även om en kurva är rationell , kanske dess offset inte är det. Till exempel är förskjutningarna för en parabel rationella kurvor, men förskjutningarna för en ellips eller en hyperbel är inte rationella, även om dessa progenitorkurvor i sig är rationella.

Begreppet generaliserar också till 3D- ytor , där det kallas en förskjuten yta eller parallell yta . Att öka en fast volym med en (konstant) avståndsförskjutning kallas ibland för dilatation . Den motsatta operationen kallas ibland beskjutning . Förskjutna ytor är viktiga vid numeriskt styrd bearbetning , där de beskriver formen på snittet som görs av en pinnfräs med kulnäsa på en treaxlig maskin. Andra former av skärbitar kan modelleras matematiskt av generella förskjutna ytor.

Parallellkurva för en parametriskt given kurva

Om det finns en regelbunden parametrisk representation ${\vec {x}}=(x(t),y(t))$ av den givna kurvan tillgänglig, den andra definitionen av en parallellkurva (s. ovan) leder till följande parametriska representation av parallellkurvan med avstånd $|d|$ :

${\vec {x}}_{d}(t)={\vec {x}}(t)+d{ \vec {n}}(t)$ med enheten normal ${\vec {n}}(t)$ .

I kartesiska koordinater:

$x_{d}(t)=x(t)+{\frac { d\;y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}$

$y_{d}(t)=y(t)-{\frac {d\;x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{ 2}}}}\ .$

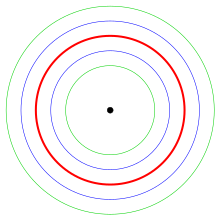
Avståndsparametern $d$ kan vara negativ. I det här fallet får man en parallell kurva på motsatta sidan av kurvan (se diagram över en cirkels parallella kurvor). Man kan enkelt kontrollera att en parallell kurva för en linje är en parallell linje i sunt förnuft, och att den parallella kurvan för en cirkel är en koncentrisk cirkel.

Geometriska egenskaper:

• ${\vec {x}}'_{d}(t)\parallel {\vec {x}}'(t),\quad$ det betyder: tangentvektorerna för en fast parameter är parallella.
• $k_{d}(t)={\frac {k(t)}{1+dk(t)}},\quad$ med $k(t)$ kurvaturen för den givna kurvan och $k_{d}(t)$ kurvaturen för parallellkurvan för parameter $\displaystyle t }$ { .
• $R_{d}(t)=R(t)+d,\quad$ med $R(t)$ radien för krökning för den givna kurvan och $R_{d}(t)$ krökningsradien för den parallella kurvan för parameter $t$ .
• När de finns är de oskulerande cirklarna till parallella kurvor vid motsvarande punkter koncentriska.
• När det gäller parallella linjer är en normal linje till en kurva också normal till dess paralleller.
• När parallella kurvor konstrueras kommer de att ha spetsar när avståndet från kurvan matchar krökningsradien . Det här är de punkter där kurvan berör evolutionen .
• Om stamfaderkurvan är en gräns för en plan mängd och dess parallellkurva är utan självskärningar, är den senare gränsen för Minkowski-summan av den plana mängden och skivan med den givna radien.

Om den givna kurvan är polynom (vilket betyder att $x(t)$ och $y(t)$ är polynom), så är de parallella kurvorna vanligtvis inte polynom. I CAD-området är detta en nackdel, eftersom CAD-system använder polynom eller rationella kurvor. För att få åtminstone rationella kurvor måste kvadratroten av representationen av parallellkurvan vara lösbar. Sådana kurvor kallas pytagoreiska hodografkurvor och undersöktes av RT Farouki.

Parallella kurvor av en implicit kurva

Parallella kurvor för den implicita kurvan (röd) med ekvation $x^{4}+y^{4}-1=0$

I allmänhet är den analytiska representationen av en parallell kurva av en implicit kurva inte möjlig. Endast för de enkla fallen av linjer och cirklar kan de parallella kurvorna lätt beskrivas. Till exempel:

Linje $\;f(x,y)=x+y-1=0\;$ → avståndsfunktion: ${\displaystyle \;h(x,y)={\frac {x+y-1}{\sqrt {2}}}=d\;} (Hesse normalform$ )

Cirkel $\;f(x,y)=x^{2}+y^{2}-1=0\;$ → avståndsfunktion: $\;h(x,y)={\sqrt {x^{2}+y^{2}}}-1=d\;.$

Generellt sett, förutsatt att vissa förhållanden antas, kan man bevisa förekomsten av en orienterad avståndsfunktion $h(x,y)$ . I praktiken måste man behandla det numeriskt. Med tanke på parallella kurvor är följande sant:

• Parallellkurvan för avstånd d är nivåuppsättningen h $\displaystyle h(x,y)=d}$ ​​för motsvarande orienterade avståndsfunktion $h$ .

Avståndsfunktionens egenskaper:

• $|\operatörsnamn {grad} h({\vec {x}})|=1\;,$
• $h({\vec {x}}+d\operatörsnamn {grad} h({\vec {x} }))=h({\vec {x}})+d\;,$
• $\operatörsnamn {grad} h({\vec {x}}+d\operatörsnamn {grad} h({\vec {x}}))=\operatörsnamn {grad} h({\vec {x}} )\;.$

Exempel: Diagrammet visar parallella kurvor för den implicita kurvan med ekvation $\;f(x,y)=x^{4}+y^{4}-1=0\;.$ Anmärkning: Kurvorna $\;f(x,y)=x^{4}+y^{4}-1=d\;$ är inte parallella kurvor, eftersom $\;|\operatörsnamn {grad} f(x,y)|=1\;$ är inte sant i intresseområdet.

Ytterligare exempel

Involuter av en cirkel

• Involuterna i en given kurva är en uppsättning parallella kurvor . Till exempel: evolventerna i en cirkel är parallella spiraler (se diagram).

Och:

• En parabel har som (tvåsidiga) förskjutningar rationella kurvor av grad 6.
• En hyperbel eller en ellips har som (tvåsidiga) förskjutningar en algebraisk kurva på grad 8.
• En Bézier-kurva av grad n har som (tvåsidiga) förskjutningar av algebraiska kurvor av grad 4 n − 2 . Speciellt har en kubisk Bezier-kurva som (tvåsidiga) förskjutningar av algebraiska kurvor av grad 10.

Parallell kurva till en kurva med hörn

Parallella kurvor till en kurva med en diskontinuerlig normal runt ett hörn

När du bestämmer skärbanan för en del med ett skarpt hörn för bearbetning måste du definiera den parallella (offset) kurvan till en given kurva som har en diskontinuerlig normal i hörnet. Även om den givna kurvan inte är jämn vid det skarpa hörnet, kan dess parallellkurva vara jämn med en kontinuerlig normal, eller så kan den ha spetsar när avståndet från kurvan matchar krökningsradien vid det skarpa hörnet.

Vanliga fans

Som beskrivits ovan , den parametriska representationen av en parallell kurva, ${\vec {x}}_{d}(t)$ , till en given kurva, ${\vec {x}}(t)$ , med avstånd $|d|$ är:

${\vec {x}}_{d}(t)={\vec {x}}(t)+d{ \vec {n}}(t)$ med enheten normal ${\vec {n}}(t)$ .

Vid ett skarpt hörn ( $t=t_{c}$ ), normalen till ${\vec {x}}(t_{c})$ ges av ${\vec {n}}(t_{c})$ är diskontinuerlig, vilket betyder den ensidiga gränsen för normalen från vänster ${\vec {n}}(t_{c}^{-})$ är olik gränsen från höger ${\vec {n}}(t_{c}^{+})$ . Matematiskt,

${\vec {n}}( t_{c}^{-})=\lim _{t\to t_{c}^{-}}{\vec {n}}(t)\neq {\vec {n}}(t_{c} ^{+})=\lim _{t\to t_{c}^{+}}{\vec {n}}(t)$ .

Normal fläkt för att definiera parallella kurvor runt ett skarpt hörn

Vi kan dock definiera en normal fläkt ${\vec {n}}_{f}(\alpha )$ som ger en interpolant mellan ${\ vec {n}}(t_{c}^{-})$ och ${\vec {n}}(t_{c}^{+})$ och använd ${\vec {n}}_{f}(\alpha )$ i stället för ${\vec {n}}(t_{c})$ vid det skarpa hörnet:

${\vec {n}}_{f}(\alpha )={\frac {(1-\alpha ){\vec {n}}(t_{c}^{-})+\ alfa {\vec {n}}(t_{c}^{+})}{\lVert (1-\alpha ){\vec {n}}(t_{c}^{-})+\alpha {\ vec {n}}(t_{c}^{+})\rVert }},\quad$ där $0<\alpha <1$ .

Den resulterande definitionen av den parallella kurvan ${\vec {x}}_{d}(t)$ ger det önskade beteendet:

${\vec {x}}_{d}(t)={\begin{cases}{\vec {x}}(t)+d{\vec {n}}( t),&{\text{if }}t<t_{c}{\text{ eller }}t>t_{c}\\{\vec {x}}(t_{c})+d{\vec {n}}_{f}(\alpha ),&{\text{if }}t=t_{c}{\text{ där }}0<\alpha <1\end{cases}}$

Algoritmer

I allmänhet är den parallella kurvan för en Bézier-kurva inte en annan Bézier-kurva, ett resultat bevisat av Tiller och Hanson 1984. I praktiken används alltså approximationstekniker. Varje önskad noggrannhetsnivå är möjlig genom att upprepade gånger dela upp kurvan, även om bättre tekniker kräver färre underavdelningar för att uppnå samma nivå av noggrannhet. En undersökning från 1997 av Elber, Lee och Kim citeras flitigt, även om bättre tekniker har föreslagits på senare tid. En modern teknik baserad på kurvanpassning , med referenser och jämförelser med andra algoritmer, samt JavaScript-källkod med öppen källkod, publicerades i ett blogginlägg i september 2022.

En annan effektiv algoritm för avräkning är nivåmetoden som beskrivs av Kimmel och Bruckstein (1993).

Parallella (offset) ytor

Offset yta av en komplex oregelbunden form

Förskjutna ytor är viktiga vid numeriskt styrd bearbetning , där de beskriver formen på snittet som görs av en pinnfräs med kulnäsa på en treaxlig fräs. Om det finns en vanlig parametrisk representation ${\vec {x}}(u, v)=(x(u,v),y(u,v),z(u,v))$ av den givna tillgängliga ytan, generaliserar den andra definitionen av en parallell kurva (se ovan) till följande parametriska representation av den parallella ytan med avstånd $|d|$ :

${\vec {x}}_{d}(u,v)={\vec {x }}(u,v)+d{\vec {n}}(u,v)$ med enheten normal ${\vec {n}}_{d}(u,v)={{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}} \over {|{{\partial {\vec {x}} \over \partial u}\times {\partial {\vec {x}} \over \partial v}}|}}$ .

Avståndsparameter $d$ kan också vara negativ. I det här fallet får man en parallell yta på motsatt sida av ytan (se liknande diagram på en cirkels parallella kurvor). Man kontrollerar lätt: en parallell yta av ett plan är ett parallellt plan i sunt förnuft och den parallella ytan av en sfär är en koncentrisk sfär.

Geometriska egenskaper:

• ${\partial {\vec {x}}_{d} \over \partial u}\ parallell {\partial {\vec {x}} \over \partial u},\quad {\partial {\vec {x}}_{d} \over \partial v}\parallel {\partial {\vec {x }} \over \partial v},\quad$ det betyder: tangentvektorerna för fasta parametrar är parallella.
• ${\vec {n}}_{d}(u,v)=\pm {\vec {n}}(u, v),\quad$ det betyder: normalvektorerna för fasta parametrar matchar riktningen.
• $S_{d}=(1+dS)^{-1}S,\quad$ där $S_{d}$ och ${ \displaystyle S}$ är formoperatorerna för ${\vec {x}}_{d}$ respektive ${\vec {x}}$ .

De huvudsakliga krökningarna är formoperatorns egenvärden , de huvudsakliga krökningsriktningarna är dess egenvektorer , den Gaussiska krökningen är dess determinant , och medelkurvaturen är halva dess spår .

• $S_{d}^{-1}=S^{-1}+dI,\quad$ där $S_{d}^ {-1}$ och $S^{-1}$ är inverserna av formoperatorerna för ${\vec {x}}_{d}$ och ${\ displaystyle {\vec {x}}}$ , respektive.

De huvudsakliga krökningsradierna är egenvärdena för inversen av formoperatorn , de huvudsakliga krökningsriktningarna är dess egenvektorer , den reciproka av den Gaussiska krökningen är dess determinant , och medelkurvaturradien är halva dess spår .

Notera likheten med de geometriska egenskaperna hos parallella kurvor .

Generaliseringar

Problemet generaliserar ganska tydligt till högre dimensioner, t.ex. till förskjutna ytor, och något mindre trivialt till rörytor . Observera att terminologin för de högre dimensionella versionerna varierar ännu mer än i det plana fallet, t.ex. talar andra författare om parallella fibrer, band och rör. För kurvor inbäddade i 3D-ytor kan förskjutningen tas längs en geodetisk .

Ett annat sätt att generalisera det är (även i 2D) att överväga ett variabelt avstånd, t.ex. parametriserat av en annan kurva. Man kan till exempel stryka (kuvert) med en ellips istället för cirkel som det är möjligt till exempel i METAFONT .

Ett hölje av ellipser som bildar två generella offsetkurvor över och under en given kurva

På senare tid har Adobe Illustrator lagt till något liknande möjligheter i version CS5 , även om kontrollpunkterna för den variabla bredden är visuellt specificerade. I sammanhang där det är viktigt att skilja mellan konstant och variabel avståndskompensation används ibland förkortningarna CDO och VDO.

Allmänna offsetkurvor

Antag att du har en regelbunden parametrisk representation av en kurva, ${\vec {x}}(t)=(x(t),y( t))$ , och du har en andra kurva som kan parametreras med dess normalenhet, ${\displaystyle {\vec {d}}({\vec {n}})} ,$ där normalen av ${\displaystyle {\vec {d}}({\vec {n}})={\vec {n}}} ($ denna parametrering som normal finns för kurvor vars krökning är strikt positiv eller negativ, och därmed konvex, jämn och inte rak). Den parametriska representationen av den allmänna offsetkurvan för ${\vec {x}}(t)$ förskjuten med ${\vec {d}}({\vec {n}})$ är:

${\displaystyle {\vec {x}}_{d}(t)={\vec {x}}(t )+{\vec {d}}({\vec {n}}(t)),\quad } där n$ → $displaystyle {\vec {n}}(t)}$ är enhetens normala för ${\vec {x}}(t)$ .

Observera att trivaloffset, ${\displaystyle {\vec {d}}({\vec {n}})=d{\vec {n}}} ,$ ger dig vanlig parallell (aka, offset) kurvor.

Geometriska egenskaper:

• ${\vec {x}}'_{d}(t)\parallel {\vec {x}}'(t),\quad$ det betyder: tangentvektorerna för en fast parameter är parallella.
• När det gäller parallella linjer är en normal till en kurva också normal till dess allmänna förskjutningar.
• $t)}}}},\quad }$$k_{d}(t)={\dfrac {k(t)}{1+{\dfrac {k (t)}{k_{n$ ( med $k_{d}(t)$ krökningen för den allmänna offsetkurvan, ${ \displaystyle k(t)}$ krökningen av ${\vec {x}}(t)$ , och $k_{n}(t)$ krökningen för ${\vec {d}}({\vec {n}}(t))$ för parameter $t$ .
• ${\displaystyle R_{d}(t)=R(t)+R_{n}(t),$$R_{d}(t)$ quad krökningsradien för den allmänna offsetkurvan, $R(t)$ krökningsradien för $\displaystyle {\vec { x}}(t)}$ { , och $R_{n}(t)$ krökningsradien för ${\vec {d}}( {\vec {n}}(t))$ för parameter $t$ .
• När generella offsetkurvor konstrueras kommer de att ha cusps när kurvans krökning matchar offsetens krökning. Det här är de punkter där kurvan berör evolutionen .

Allmänna förskjutna ytor

Allmänna offsetytor beskriver formen på snitt som görs av en mängd olika skär som används av treaxliga pinnfräsar vid numeriskt styrd bearbetning . Antag att du har en regelbunden parametrisk representation av en yta, ${\displaystyle {\vec {x} }(u,v)=(x(u,v),y(u,v),z(u,v))} , och du har en$ andra yta som kan parametriseras av dess normalenhet, ${\vec {d}}({\vec {n}})$ , där normalen för ${\vec {d}}({\vec {n}})={\vec {n}}$ (denna parametrisering av normal finns för ytor vars Gaussiska krökning är strikt positiv och därmed konvex, jämn och inte platt). Den parametriska representationen av den allmänna offsetytan för ${\vec {x}}(t)$ förskjuten med ${\vec {d}}({\vec {n}})$ är:

${\displaystyle {\vec {x}}_{d}(u,v)={ \vec {x}}(u,v)+{\vec {d}}({\vec {n}}(u,v)),\quad } där n → ($ u $\ vec {n}}(u,v)}$ är enhetsnormalen för ${\vec {x}}(u,v)$ .

Observera att trivaloffset, ${\displaystyle {\vec {d}}({\vec {n}})=d{\vec {n}}},$ ger dig vanlig parallell (aka, offset) ytor.

Geometriska egenskaper:

• När det gäller parallella linjer är tangentplanet för en yta parallell med tangentplanet för dess allmänna förskjutningar.
• När det gäller parallella linjer är en normal till en yta också normal till dess allmänna förskjutningar.
• $S_{d}=(1+SS_{n}^{-1})^{-1}S,\quad$ där $S_{d},S,$ och $S_{n}$ är formoperatorerna för ${\vec {x}}_{d },{\vec {x}},$ respektive ${\vec {d}}({\vec {n}})$ .

De huvudsakliga krökningarna är formoperatorns egenvärden , de huvudsakliga krökningsriktningarna är dess egenvektorer , den Gaussiska krökningen är dess determinant , och medelkurvaturen är halva dess spår .

• $S_{d}^{-1}=S^{-1}+S_{n}^{-1},\quad$ där $S_{d}^{-1},S^{-1}$ och $S_{n}^{-1}$ är inverserna av formen operatorer för ${\vec {x}}_{d},{\vec {x}},$ och ${\vec {d}} ({\vec {n}})$ , respektive.

De huvudsakliga krökningsradierna är egenvärdena för inversen av formoperatorn , de huvudsakliga krökningsriktningarna är dess egenvektorer , den reciproka av den Gaussiska krökningen är dess determinant , och medelkurvaturradien är halva dess spår .

Observera likheten med de geometriska egenskaperna hos allmänna offsetkurvor .

Härledning av geometriska egenskaper för generella offset

De geometriska egenskaperna som anges ovan för generella offsetkurvor och ytor kan härledas för offset med godtyckliga dimensioner. Antag att du har en regelbunden parametrisk representation av en n-dimensionell yta, ${\displaystyle {\vec {x}}({\vec {u}})} ,$ där dimensionen för ${\vec {u}}$ är n-1. Antag också att du har en andra n-dimensionell yta som kan parametriseras av dess normalenhet, ${\displaystyle {\vec {d}}({\vec {n}})} ,$ där normalen för ${\displaystyle {\vec {d}}({\vec {n}})={\vec {n}}} ($ denna parametrisering som normal finns för ytor vars Gaussiska krökning är strikt positiv, och därmed konvex, slät och inte platt). Den parametriska representationen av den allmänna offsetytan för ${\vec {x}}({\vec {u}})$ förskjuten med ${\vec { d}}({\vec {n}})$ är:

${\vec {x}}_{d}({\vec {u}})= {\vec {x}}({\vec {u}})+{\vec {d}}({\vec {n}}({\vec {u}})),\quad$ där ${\displaystyle {\vec {n}}({\vec {u}})} är$ enhetsnormalen för ${\vec {x}}({\vec {u }})$ . (Trivaloffset, ${\displaystyle {\vec {d}}({\vec {n}})=d{\vec {n}}} ,$ ger dig vanliga parallella ytor .)

Lägg först märke till att normalen för ${\vec {x}}({\vec {u}})=$ normalen för ${\vec {d}}({\vec {n}}({\vec {u}}))={\vec {n}}({\vec {u}} ),$ per definition. Nu kommer vi att tillämpa differentialen wrt ${\vec {u}}$ på ${\vec {x}}_{d}$ , vilket ger oss dess tangentvektorer som spänner över dess tangentplan.

$\partial {\vec {x}}_{d}({\vec {u }})=\partial {\vec {x}}({\vec {u}})+\partial {\vec {d}}({\vec {n}}({\vec {u}}))$

Observera att tangentvektorerna för ${\vec {x}}_{d}$ är summan av tangentvektorerna för ${\vec {x}}({\ vec {u}})$ och dess offset ${\displaystyle {\vec {d}}({\vec {n}})} ,$ som delar samma enhet normal. Således delar den allmänna offsetytan samma tangentplan och normal med ${\vec {x}}({\vec {u}})$ och ${\vec {d}}({\vec {n}}({\vec {u}}))$ . Det överensstämmer med kuvertens natur.

Vi betraktar nu Weingartensekvationerna för formoperatorn , som kan skrivas som $\partial {\vec {n}}=-\partial {\vec {x}}S$ . Om $S$ är inverterbar, $\partial {\vec {x}}=-\partial {\vec {n}}S^{-1}$ . Kom ihåg att de huvudsakliga krökningarna av en yta är egenvärdena för formoperatorn, de huvudsakliga krökningsriktningarna är dess egenvektorer , Gauss krökning är dess determinant och medelkurvaturen är halva dess spår . Inversen av formoperatorn har samma värden för krökningsradier.

Genom att ersätta differentialen för ${\displaystyle {\vec {x}}_{d}} i ekvationen$ får vi:

$\partial {\vec {x}}_{d}=\partial {\vec {x}}-\partial {\vec { n}}S_{n}^{-1},\quad$ där $S_{n}$ är formoperatorn för ${\vec {d }}({\vec {n}}({\vec {u}}))$ .

Därefter använder vi Weingartens ekvationer igen för att ersätta $\partial {\vec {n}}$ :

$\partial {\vec {x}}_{d}=\partial {\vec {x}}+\partial {\vec {x}}SS_{n}^{-1},\quad$ där $S$ är formoperatorn för ${\vec {x}}({\vec { u}})$ .

Sedan löser vi $\partial {\vec {x}}$ och multiplicerar båda sidor med $-S$ för att komma tillbaka till Weingartens ekvationer , denna gång för ${ \displaystyle \partial {\vec {x}}_{d}}$ :

$\partial {\vec {x}}_{d}(I+SS_{n}^{-1})^ {-1}=\partiell {\vec {x}},$

$-\partial {\vec {x}}_{d}(I+SS_{n}^{-1})^{-1}S=-\partial {\vec {x}}S=\ partiell {\vec {n}}.$

Således, ${\displaystyle S_{d}=(I+SS_{n}^{-1})^{-1}S} ,$ och invertering av båda sidor ger oss, $S_{d}^{-1}=S^{-1}+S_{n}^{-1}$ .

Se även

• Bumpmapping
• Distansfunktion och signerad distansfunktion
• Avståndsfält
• Offset tryck
• Rörformade kvarter

• Josef Hoschek: Förskjutna kurvor i planet. I: CAD. 17 (1985), S. 77-81.
• Takashi Maekawa: En översikt över förskjutna kurvor och ytor. I: CAD. 31 (1999), S. 165-173.

Vidare läsning

• Farouki, RT; Neff, CA (1990). "Analytiska egenskaper hos planförskjutningskurvor". Datorstödd geometrisk design . 7 (1–4): 83–99. doi : 10.1016/0167-8396(90)90023-K .
•   Piegl, Les A. (1999). "Beräkning av förskjutningar av NURBS-kurvor och ytor". Datorstödd design . 31 (2): 147–156. CiteSeerX 10.1.1.360.2793 . doi : 10.1016/S0010-4485(98)00066-9 .
•   Porteous, Ian R. (2001). Geometric Differentiation: For the Intelligence of Curves and Surfaces (2nd ed.). Cambridge University Press. s. 1–25. ISBN 978-0-521-00264-6 .
•   Patrikalakis, Nicholas M.; Maekawa, Takashi (2010) [2002]. Shape Interrogation för datorstödd design och tillverkning . Springer Science & Business Media. Kapitel 11. Offsetkurvor och ytor. ISBN 978-3-642-04074-0 . Gratis onlineversion .
• Anton, François; Emiris, Ioannis Z.; Mourrain, Bernard; Teillaud, Monique (maj 2005). "O-värdet är inställt på en algebraisk kurva och en applikation på koniker". Internationell konferens om beräkningsvetenskap och dess tillämpningar . Singapore: Springer Verlag. s. 683–696.
•   Farouki, Rida T. (2008). Pythagoras-hodografkurvor: algebra och geometri oskiljaktiga . Springer Science & Business Media. s. 141–178. ISBN 978-3-540-73397-3 . Sidorna som anges är det allmänna och inledande materialet.
•   Au, CK; Ma, Y.-S. (2013). "Beräkning av offsetkurvor med hjälp av en avståndsfunktion: Att ta itu med en nyckelutmaning vid generering av skärverktygsbanor". I Ma, Y.-S. (red.). Semantisk modellering och interoperabilitet i produkt- och processteknik: A Technology for Engineering Informatics . Springer Science & Business Media. s. 259–273. ISBN 978-1-4471-5073-2 .

externa länkar

• Parallella kurvor på MathWorld
• Visual Dictionary of Plane Curves Xah Lee
• http://library.imageworks.com/pdfs/imageworks-library-offset-curve-deformation-from-Skeletal-Anima.pdf applikation till animering; patenterad som http://www.google.com/patents/US8400455
• http://www2.uah.es/fsegundo/Otros/Offset/16-SanSegundoSendraSendra-1532.pdf