Adiabatisk process

Inom termodynamik är en adiabatisk process (grekiska: adiábatos , "oframkomlig") en typ av termodynamisk process som sker utan att överföra värme eller massa mellan det termodynamiska systemet och dess miljö . Till skillnad från en isoterm process överför en adiabatisk process energi till omgivningen endast som arbete . Som ett nyckelbegrepp inom termodynamiken stöder den adiabatiska processen teorin som förklarar termodynamikens första lag .

Vissa kemiska och fysikaliska processer sker för snabbt för att energi ska komma in i eller lämna systemet som värme, vilket möjliggör en bekväm "adiabatisk approximation". Till exempel använder den adiabatiska flamtemperaturen denna approximation för att beräkna den övre gränsen för flamtemperatur genom att anta att förbränning inte förlorar någon värme till sin omgivning.

Inom meteorologi och oceanografi producerar adiabatisk kylning kondensering av fukt eller salthalt, vilket övermättar paketet . Därför måste överskottet tas bort. Där blir processen en pseudo-adiabatisk process där det flytande vattnet eller saltet som kondenserar antas avlägsnas vid bildning genom idealiserad momentan utfällning . Den pseudoadiabatiska processen definieras endast för expansion eftersom ett komprimerat paket blir varmare och förblir undermättat.

Beskrivning

En process utan överföring av värme till eller från ett system, så att $Q = 0$ , kallas adiabatiskt, och ett sådant system sägs vara adiabatiskt isolerat. Det förenklade antagandet som ofta görs är att en process är adiabatisk. Exempelvis antas kompressionen av en gas i en cylinder i en motor ske så snabbt att på tidsskalan för kompressionsprocessen kan lite av systemets energi överföras ut som värme till omgivningen. Även om cylindrarna inte är isolerade och är ganska ledande, är den processen idealiserad för att vara adiabatisk. Detsamma kan sägas vara sant för utbyggnadsprocessen av ett sådant system.

Antagandet om adiabatisk isolering är användbart och kombineras ofta med andra sådana idealiseringar för att beräkna en bra första approximation av ett systems beteende. Till exempel, enligt Laplace , när ljud färdas i en gas, finns det ingen tid för värmeledning i mediet, och därför är ljudutbredningen adiabatisk. För en sådan adiabatisk process elasticitetsmodulen ( Youngs modul ) uttryckas som $E = γP$ , där $γ$ är förhållandet mellan specifika värme vid konstant tryck och vid konstant volym ( $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} γ = C p / C v$ ) och $P$ är gasens tryck.

Olika tillämpningar av det adiabatiska antagandet

För ett slutet system kan man skriva termodynamikens första lag som: $Δ U = Q - W$ , där $Δ U$ betecknar förändringen av systemets inre energi, $Q$ mängden energi som tillförs det som värme, och $W$ det utförda arbetet. av systemet på dess omgivning.

Om systemet har så styva väggar att arbete inte kan överföras in eller ut ( $W = 0$ ), och väggarna inte är adiabatiska och energi tillförs i form av värme ( $Q > 0$ ), och det inte sker någon fasförändring, då temperaturen i systemet kommer att stiga.
Om systemet har så styva väggar att tryck-volymarbete inte kan utföras, men väggarna är adiabatiska ( $Q = 0$ ), och energi tillförs som isokoriskt (konstant volym) arbete i form av friktion eller omrörning av en trögflytande vätska inom systemet ( $W < 0$ ), och det inte sker någon fasförändring, kommer temperaturen i systemet att stiga.
Om systemväggarna är adiabatiska ( $Q = 0$ ) men inte stela ( $W \neq 0$ ), och i en fiktiv idealiserad process tillförs energi till systemet i form av friktionsfritt, icke-visköst tryck-volymarbete ( $W < 0$ ), och det inte finns någon fasförändring, kommer systemets temperatur att stiga. En sådan process kallas en isentrop process och sägs vara "reversibel". Idealiskt, om processen vänds om, skulle energin kunna återvinnas helt och hållet som arbete utfört av systemet. Om systemet innehåller en komprimerbar gas och minskar i volym, minskar osäkerheten i gasens position, och det verkar minska systemets entropi, men systemets temperatur kommer att stiga när processen är isentropisk ( $Δ S = 0$ ). Skulle arbetet läggas till på ett sådant sätt att friktion eller viskösa krafter verkar inom systemet, så är processen inte isentropisk, och om det inte sker någon fasförändring kommer temperaturen i systemet att stiga, processen sägs vara "oåterkallelig", och det arbete som lagts till systemet är inte helt återvinningsbart i form av arbete.
Om väggarna i ett system inte är adiabatiska, och energi överförs som värme, överförs entropin till systemet med värmen. En sådan process är varken adiabatisk eller isentropisk, med $Q > 0$ och $Δ S > 0$ enligt termodynamikens andra lag .

Naturligt förekommande adiabatiska processer är irreversibla (entropi produceras).

Överföringen av energi som arbete till ett adiabatiskt isolerat system kan föreställas vara av två idealiserade extrema slag. I ett sådant slag produceras ingen entropi inom systemet (ingen friktion, viskös avledning, etc.), och arbetet är endast tryck-volymarbete (betecknat med P $d V)$ . I naturen uppstår denna idealtyp endast ungefär eftersom den kräver en oändligt långsam process och inga källor till förlust.

Den andra extrema typen av arbete är isokoriskt arbete ( $d V = 0$ ), för vilket energi tillförs som arbete enbart genom friktion eller viskös avledning inom systemet. En omrörare som överför energi till en viskös vätska i ett adiabatiskt isolerat system med stela väggar, utan fasförändring, kommer att orsaka en temperaturhöjning av vätskan, men det arbetet är inte återvinningsbart. Isokoriskt arbete är oåterkalleligt. Termodynamikens andra lag konstaterar att en naturlig process, överföring av energi som arbete, alltid består åtminstone av isokoriskt arbete och ofta båda dessa extrema typer av arbete. Varje naturlig process, adiabatisk eller inte, är irreversibel, med $Δ S > 0$ , eftersom friktion eller viskositet alltid är närvarande i viss utsträckning.

Adiabatisk uppvärmning och kylning

Den adiabatiska kompressionen av en gas orsakar en ökning av temperaturen hos gasen. Adiabatisk expansion mot tryck, eller en fjäder, orsakar temperaturfall. Däremot fri expansion en isotermisk process för en idealisk gas.

Adiabatisk uppvärmning uppstår när trycket hos en gas ökas genom arbete som utförs på den av dess omgivning, t.ex. en kolv som komprimerar en gas som finns i en cylinder och höjer temperaturen där värmeledning genom väggar i många praktiska situationer kan vara långsam jämfört med kompressionstid. Detta finner praktisk tillämpning i dieselmotorer som är beroende av bristen på värmeavledning under kompressionsslaget för att höja bränsleångtemperaturen tillräckligt för att antända den.

Adiabatisk uppvärmning inträffar i jordens atmosfär när en luftmassa sjunker, till exempel i en Katabatisk vind , Foehn-vind eller Chinook-vind som flyter nedför en bergskedja. När ett luftpaket faller ner ökar trycket på paketet. På grund av denna tryckökning minskar paketets volym och dess temperatur ökar när arbetet utförs på luftpaketet, vilket ökar dess inre energi, vilket visar sig genom en ökning av temperaturen hos den luftmassan. Luftpaketet kan bara långsamt avleda energin genom ledning eller strålning (värme), och till en första approximation kan den betraktas som adiabatiskt isolerad och processen som en adiabatisk process.

Adiabatisk kylning uppstår när trycket på ett adiabatiskt isolerat system minskar, vilket gör att det kan expandera, vilket får det att utföra arbete på sin omgivning. När trycket som appliceras på ett gaspaket reduceras tillåts gasen i paketet att expandera; när volymen ökar sjunker temperaturen när dess inre energi minskar. Adiabatisk kylning sker i jordens atmosfär med orografiskt lyft och lä vinkar , och detta kan bilda pilei eller linsformiga moln .

Delvis på grund av adiabatisk kylning i bergsområden, inträffar snöfall sällan i vissa delar av Saharaöknen .

Adiabatisk kylning behöver inte involvera en vätska. En teknik som används för att nå mycket låga temperaturer (tusendelar och till och med miljondelar av en grad över absolut noll) är via adiabatisk avmagnetisering , där förändringen i magnetfältet på ett magnetiskt material används för att ge adiabatisk kylning. Dessutom kan innehållet i ett expanderande universum beskrivas (till första ordningen) som en adiabatiskt kylande vätska. (Se universums värmedöd .)

Stigande magma genomgår också adiabatisk kylning före utbrott, särskilt viktigt i fallet med magma som stiger snabbt från stora djup som kimberliter .

I jordens konvektionsmantel (astenosfären) under litosfären är manteltemperaturen ungefär en adiabat. Den lätta temperaturminskningen med grunda djup beror på att trycket minskar ju grundare materialet är i jorden.

Sådana temperaturförändringar kan kvantifieras med hjälp av den ideala gaslagen eller den hydrostatiska ekvationen för atmosfäriska processer.

I praktiken är ingen process riktigt adiabatisk. Många processer förlitar sig på en stor skillnad i tidsskalor för processen av intresse och hastigheten för värmeavledning över en systemgräns, och är således approximerade genom att använda ett adiabatiskt antagande. Det finns alltid en viss värmeförlust, eftersom det inte finns några perfekta isolatorer.

Idealisk gas (reversibel process)

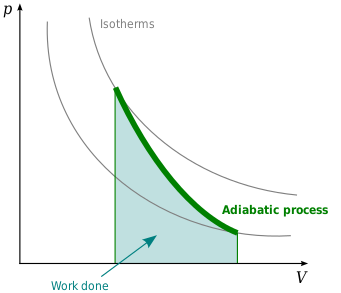
För ett enkelt ämne, under en adiabatisk process där volymen ökar, måste den inre energin hos det arbetande ämnet minska

Den matematiska ekvationen för en idealgas som genomgår en reversibel (dvs ingen entropigenerering) adiabatisk process kan representeras av den polytropiska processekvationen

PV^{\gamma }={\text{konstant}},

där $P$ är tryck, $V$ är volym och $γ$ är det adiabatiska indexet eller värmekapacitetsförhållandet definierat som

\gamma ={\frac {C_{P}}{C_{V}}}={\frac {f+2}{f}}.

Här är $C P$ den specifika värmen för konstant tryck, $C V$ är den specifika värmen för konstant volym, och $f$ är antalet frihetsgrader (3 för en monoatomisk gas, 5 för en diatomisk gas eller en gas av linjära molekyler som t.ex. koldioxid).

För en monoatomisk idealgas, $γ = 5/3 , och för .,$ en diatomisk gas $γ = 7/5, ($ som kväve och syre luftens huvudkomponenter) Observera att formeln ovan endast är tillämplig på klassiska idealgaser (det vill säga gaser långt över absolut nolltemperatur) och inte Bose-Einstein- eller Fermi-gaser .

Man kan också använda den ideala gaslagen för att skriva om ovanstående förhållande mellan $P$ och $V$ as

P^{1-\gamma }T^{\gamma }={\text{konstant}},

TV^{\gamma -1}={\text{konstant}}.

där T är den absoluta eller termodynamiska temperaturen .

Exempel på adiabatisk kompression

Kompressionsslaget i en bensinmotor kan användas som ett exempel på adiabatisk kompression. Modellantagandena är: cylinderns okomprimerade volym är en liter (1 L = 1000 cm ³ = 0,001 m ³ ); gasen inuti är luften som består av endast molekylärt kväve och syre (alltså en diatomisk gas med 5 frihetsgrader, och så $γ = 7 / 5$ ); motorns kompressionsförhållande är 10:1 (det vill säga 1 L volymen av okomprimerad gas reduceras till 0,1 L av kolven); och den okomprimerade gasen har ungefär rumstemperatur och tryck (en varm rumstemperatur på ~27 °C, eller 300 K, och ett tryck på 1 bar = 100 kPa, dvs. typiskt atmosfärstryck vid havsnivån).

_ \displaystyle {\begin{aligned}&P_{1}V_{1}^{\gamma }=\mathrm {constant} _{1}=100\,000~{\text{Pa}}\times (0,001~{ \text{m}}^{3})^{\frac {7}{5}}\\&=10^{5}\times 6.31\times 10^{-5}~{\text{Pa}} \,{\text{m}}^{21/5}=6.31~{\text{Pa}}\,{\text{m}}^{21/5},\end{aligned}}}

så den adiabatiska konstanten för detta exempel är cirka 6,31 Pa m ^4,2 .

Gasen komprimeras nu till en volym på 0,1 L (0,0001 m ³ ), vilket vi antar sker tillräckligt snabbt för att ingen värme kommer in i eller lämnar gasen genom väggarna. Den adiabatiska konstanten förblir densamma, men med det resulterande trycket okänt

{2}^{\gamma }= \mathrm {konstant} _{1}=6.31~{\text{Pa}}\,{\text{m}}^{21/5}=P\ gånger (0.0001~{\text{m}}^{ 3})^{\frac {7}{5}},}

Vi kan nu lösa det slutliga trycket

P_{2}=P_{1}\left({\frac {V_{1} {V_{2}}}\right)^{\gamma }=100\,000~{\text{Pa}}\ gånger {\text{10}}^{7/5}=2,51\ gånger 10^ {6}~{\text{Pa}}

eller 25,1 bar. Denna tryckökning är mer än ett enkelt kompressionsförhållande på 10:1 skulle indikera; detta beror på att gasen inte bara komprimeras, utan arbetet som görs för att komprimera gasen ökar också dess inre energi, vilket visar sig genom en ökning av gastemperaturen och en ytterligare ökning av trycket över vad som skulle bli resultatet av en förenklad beräkning av 10 gånger det ursprungliga trycket.

Vi kan också lösa temperaturen på den komprimerade gasen i motorcylindern med hjälp av den ideala gaslagen, PV = nRT ( n är mängden gas i mol och R gaskonstanten för den gasen). Våra initiala förhållanden är 100 kPa tryck, 1 L volym och 300 K temperatur, vår experimentella konstant ( nR ) är:

{\frac {PV}{T}}=\mathrm {konstant} _{2}={\frac {10^{5}~{\text{Pa}}\ gånger 10^{-3}~ {\text{m}}^{3}}{300~{\text{K}}}}=0,333~{\text{Pa}}\,{\text{m}}^{3}{\text {K}}^{-1}.

Vi vet att den komprimerade gasen har $V$ = 0,1 L och $P$ = 2,51 × 10 ⁶ Pa , så vi kan lösa temperaturen:

T={\frac {PV}{\mathrm {konstant} _{2}}}={\frac {2.51\times 10^{6}~{\text{Pa}}\times 10^{- 4}~{\text{m}}^{3}}{0.333~{\text{Pa}}\,{\text{m}}^{3}{\text{K}}^{-1} }}=753~{\text{K}}.

Det är en sluttemperatur på 753 K, eller 479 °C, eller 896 °F, långt över antändningspunkten för många bränslen. Detta är anledningen till att en högkompressionsmotor kräver bränslen speciellt framtagna för att inte självantända (vilket skulle orsaka knackningar på motorn när den körs under dessa temperatur- och tryckförhållanden), eller att en kompressor med en intercooler för att ge en tryckökning men med en lägre temperaturhöjning skulle vara fördelaktigt. En dieselmotor arbetar under ännu mer extrema förhållanden, med kompressionsförhållanden på 16:1 eller mer som typiskt, för att ge en mycket hög gastemperatur, vilket säkerställer omedelbar antändning av det insprutade bränslet.

Adiabatisk fri expansion av en gas

För en adiabatisk fri expansion av en idealgas , förvaras gasen i en isolerad behållare och tillåts sedan expandera i ett vakuum. Eftersom det inte finns något yttre tryck för gasen att expandera mot, är arbetet som utförs av eller på systemet noll. Eftersom denna process inte involverar någon värmeöverföring eller arbete, innebär termodynamikens första lag att den interna nettoenergiförändringen i systemet är noll. För en idealgas förblir temperaturen konstant eftersom den inre energin bara beror på temperaturen i så fall. Eftersom entropin vid konstant temperatur är proportionell mot volymen, ökar entropin i detta fall, därför är denna process oåterkallelig.

Härledning av P – V -relation för adiabatisk uppvärmning och kylning

Definitionen av en adiabatisk process är att värmeöverföringen till systemet är noll, $δQ = 0$ . Sedan, enligt termodynamikens första lag,

dU+\delta W=\delta Q=0,

()

där $dU$ är förändringen i systemets inre energi och $δW$ är arbete som utförs av systemet. Allt arbete ( $δW$ ) som utförs måste utföras på bekostnad av intern energi $U$ , eftersom ingen värme $δQ$ tillförs från omgivningen. Tryck–volymarbete $δW$ utfört av systemet definieras som

\delta W=P\,dV.

()

$P förblir$ dock inte konstant under en adiabatisk process utan förändras istället tillsammans med $V$ .

Det är önskvärt att veta hur värdena för $dP$ och $dV$ förhåller sig till varandra när den adiabatiska processen fortskrider. För en idealgas (kom ihåg idealgaslagen $PV = nRT$ ) ges den inre energin av

U=\alpha nRT=\alpha PV,

()

där $α$ är antalet frihetsgrader dividerat med 2, $R$ är den universella gaskonstanten och $n$ är antalet mol i systemet (en konstant).

Differentieringsekvation (a3) ger

dU=\alpha nR\,dT=\alpha \,d(PV)=\alpha (P\,dV+V\,dP).

()

Ekvation (a4) uttrycks ofta som $dU = nC V dT$ eftersom $C V = αR$ .

Ersätt nu ekvationerna (a2) och (a4) med ekvation (a1) för att erhålla

-P\,dV=\alpha P\,dV+\alpha V\,dP,

faktorisera $- P dV$ :

-(\alpha +1)P\,dV=\alpha V\,dP,

och dividera båda sidor med $PV$ :

-(\alpha +1){\frac {dV}{V}}=\alpha {\frac {dP}{P}}.

Efter att ha integrerat vänster och höger sida från $V 0$ till $V$ och från $P 0$ till $P$ och bytt sidor respektive,

\ln \left({\frac {P}{P_{0}}}\right)=-{\frac {\alpha +1}{\alpha }}\ln \left({\frac {V }{V_{0}}}\höger).

Exponentiera båda sidorna, ersätt $α + 1 / α$ med $γ$ , värmekapacitetsförhållandet

\left({\frac {P}{P_{0}}}\right)=\left({\frac {V}{V_{0}} }\right)^{-\gamma },

och eliminera det negativa tecknet för att få

\left({\frac {P}{P_{0}}}\right)=\left({\frac {V_{0}}{V}}\right)^{\gamma }.

Därför,

\left({\frac {P}{P_{0}}}\right)\left({\frac {V}{V_{0}}} \right)^{\gamma }=1,

och

P_{0}V_{0}^{\gamma }=PV^{\gamma }=\mathrm {konstant} .

\Delta U=\alpha RnT_{2}-\alpha RnT_{1}=\alpha Rn\Delta T.

()

Samtidigt är det arbete som utförs av tryck–volymförändringarna som ett resultat av denna process lika med

W=\int _{V_{1}}^{V_{2}}P\,dV.

()

Eftersom vi kräver att processen är adiabatisk, måste följande ekvation vara sann

\Delta U+W=0.

()

Enligt den tidigare härledningen,

PV^{\gamma }={\text{constant}}=P_{1}V_{1}^{\gamma }.

()

Omarrangering (b4) ger

P=P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }.

Att ersätta detta med (b2) ger

W=\int _{V_{1}}^{V_{2}}P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }\ ,dV.

Genom att integrera får vi uttrycket för arbete,

W=P_{1}V_{1}^{\gamma }{\frac {V_{2}^{1-\gamma }-V_{1}^{1-\gamma }}{1-\ gamma }}={\frac {P_{2}V_{2}-P_{1}V_{1}}{1-\gamma }}.

Ersätter $γ = α + 1 / α$ i andra termen,

W=-\alpha P_{1}V_{1}^{\gamma }\left(V_{2}^{1-\gamma}-V_{1}^{1-\gamma }\right) .

Ordna om,

W=-\alpha P_{1}V_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1 \höger).

Att använda den ideala gaslagen och anta en konstant molär kvantitet (som ofta händer i praktiska fall),

W=-\alpha nRT_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).

Med den kontinuerliga formeln,

{\frac {P_{2}}{P_{1}}}=\left({\frac {V_{2}}{V_{1 }}}\right)^{-\gamma },

eller

\left({\frac {P_{2}}{P_{1}}}\right)^{-{\frac {1}{\gamma }}}={\frac {V_{2}} {V_{1}}}.

Ersätter $W i det föregående uttrycket$ ,

W=-\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\höger).

Att ersätta detta uttryck och (b1) i (b3) ger

\alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^ {\frac {\gamma -1}{\gamma }}-1\right).

Förenkla,

T_{2}-T_{1}=T_{1}\left(\left({\frac { P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right),

{\frac {T_{2}}{T_{1}}}-1=\left({\frac {P_{2}}{P_{1}}}\right )^{\frac {\gamma -1}{\gamma }}-1,

T_{2}=T_{1}\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}.

Härledning av diskret formel och arbetsuttryck

Förändringen i inre energi i ett system, mätt från tillstånd 1 till tillstånd 2, är lika med

Samtidigt är det arbete som utförs av tryck–volymförändringarna som ett resultat av denna process lika med

W=\int _{V_{1}}^{V_{2}}P\,dV.

()

Eftersom vi kräver att processen är adiabatisk, måste följande ekvation vara sann

\Delta U+W=0.

()

Enligt den tidigare härledningen,

PV^{\gamma }={\text{constant}}=P_{1}V_{1}^{\gamma }.

()

Omarrangering (c4) ger

P=P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }.

Att ersätta detta med (c2) ger

W=\int _{V_{1}}^{V_{2}}P_{1}\left({\frac {V_{1}}{V}}\right)^{\gamma }\ ,dV.

Genom att integrera får vi uttrycket för arbete,

W=P_{1}V_{1}^{\gamma }{\frac {V_{2}^{1-\gamma }-V_{1}^{1-\gamma }}{1-\ gamma }}={\frac {P_{2}V_{2}-P_{1}V_{1}}{1-\gamma }}.

Ersätter $γ = α + 1 / α$ i andra termen,

W=-\alpha P_{1}V_{1}^{\gamma }\left(V_{2}^{1-\gamma}-V_{1}^{1-\gamma }\right) .

Ordna om,

W=-\alpha P_{1}V_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1 \höger).

Att använda den ideala gaslagen och anta en konstant molär kvantitet (som ofta händer i praktiska fall),

W=-\alpha nRT_{1}\left(\left({\frac {V_{2}}{V_{1}}}\right)^{1-\gamma }-1\right).

Med den kontinuerliga formeln,

{\frac {P_{2}}{P_{1}}}=\left({\frac {V_{2}}{V_{1 }}}\right)^{-\gamma },

eller

\left({\frac {P_{2}}{P_{1}}}\right)^{-{\frac {1}{\gamma }}}={\frac {V_{2}} {V_{1}}}.

Ersätter $W i det föregående uttrycket$ ,

W=-\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\höger).

Att ersätta detta uttryck och (cl) i (c3) ger

\alpha nR(T_{2}-T_{1})=\alpha nRT_{1}\left(\left({\frac {P_{2}}{P_{1}}}\right)^ {\frac {\gamma -1}{\gamma }}-1\right).

Förenkla,

T_{2}-T_{1}=T_{1}\left(\left({\frac { P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}-1\right),

{\frac {T_{2}}{T_{1}}}-1=\left({\frac {P_{2}}{P_{1}}}\right )^{\frac {\gamma -1}{\gamma }}-1,

T_{2}=T_{1}\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}.

Rita adiabater

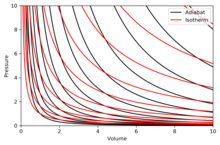
En adiabat är en kurva med konstant entropi i ett diagram. Vissa egenskaper hos adiabater på ett P – V -diagram anges. Dessa egenskaper kan avläsas från det klassiska beteendet hos idealgaser, förutom i den region där PV blir liten (låg temperatur), där kvanteffekter blir viktiga.

Varje adiabat närmar sig asymptotiskt både V -axeln och P -axeln (precis som isotermer ).
Varje adiabat skär varje isoterm exakt en gång.
En adiabat liknar en isoterm, förutom att under en expansion tappar en adiabat mer tryck än en isoterm, så den har en brantare lutning (mer vertikal).
Om isotermerna är konkava mot nordöstlig riktning (45°), så är adiabaterna konkava mot öster nordost (31°).
Om adiabater och isotermer plottas med regelbundna intervall av entropi respektive temperatur (som höjd på en konturkarta), då när ögat rör sig mot axlarna (mot sydväst), ser det att isotermernas täthet förblir konstant, men den ser tätheten av adiabater växa. Undantaget är mycket nära absolut noll, där densiteten av adiabater sjunker kraftigt och de blir sällsynta (se Nernsts sats ) . ^{[ förtydligande behövs ]}

Det högra diagrammet är ett P – V -diagram med en superposition av adiabater och isotermer:

Isotermerna är de röda kurvorna och adiabaterna är de svarta kurvorna.

Adiabaterna är isentropiska.

Volym är den horisontella axeln och tryck är den vertikala axeln.

Etymologi

Termen adiabatisk ( / ˌ æ d i ə ˈ b æ t ɪ k / ) är en anglicisering av den grekiska termen ἀδιάβατος "oframkomlig" (används av Xenophon av floder). Det används i termodynamisk mening av Rankine (1866) och antogs av Maxwell 1871 (explicit tillskriver termen Rankine). Det etymologiska ursprunget motsvarar här en omöjlighet att överföra energi som värme och att överföra materia över väggen.

Det grekiska ordet ἀδιάβατος är bildat av privativ ἀ- ("inte") och διαβατός, "framkomlig", i sin tur härstammande från διά ("genom") och βαῖνειν ("att gå, gå, komma, komma).

Begreppsmässig betydelse i termodynamisk teori

Den adiabatiska processen har varit viktig för termodynamiken sedan dess tidiga dagar. Det var viktigt i Joules arbete eftersom det gav ett sätt att nästan direkt relatera mängder värme och arbete.

Energi kan komma in i eller lämna ett termodynamiskt system omslutet av väggar som förhindrar massöverföring endast som värme eller arbete. Därför kan en mängd arbete i ett sådant system nästan direkt relateras till en ekvivalent mängd värme i en cykel med två extremiteter. Den första delen är en isokorisk adiabatisk arbetsprocess som ökar systemets inre energi ; den andra, en isokorisk och arbetslös värmeöverföring som återför systemet till sitt ursprungliga tillstånd. Följaktligen mätte Rankine mängden värme i arbetsenheter, snarare än som en kalorimetrisk kvantitet. 1854 använde Rankine en kvantitet som han kallade "den termodynamiska funktionen" som senare kallades entropi, och vid den tiden skrev han också om "kurvan för ingen värmeöverföring", som han senare kallade en adiabatisk kurva. Förutom sina två isotermiska lemmar, har Carnots cykel två adiabatiska lemmar.

För termodynamikens grunder betonades den konceptuella betydelsen av detta av Bryan, av Carathéodory och av Born. Anledningen är att kalorimetri förutsätter en typ av temperatur som redan definierats innan termodynamikens första lag, till exempel en baserad på empiriska skalor. En sådan förutsättning innebär att man gör skillnad mellan empirisk temperatur och absolut temperatur. Snarare är definitionen av absolut termodynamisk temperatur bäst att lämna tills den andra lagen är tillgänglig som en begreppsmässig grund.

På 1700-talet var lagen om energibevarande ännu inte helt formulerad eller etablerad, och värmens natur diskuterades. Ett tillvägagångssätt för dessa problem var att betrakta värme, mätt med kalorimetri, som ett primärt ämne som bevaras i kvantitet. Vid mitten av artonhundratalet erkändes det som en form av energi, och lagen om energins bevarande erkändes därmed också. Den åsikt som så småningom etablerade sig, och för närvarande betraktas som rätt, är att lagen om energibevarande är ett primärt axiom, och att värme ska analyseras som konsekvens. I detta ljus kan värme inte vara en komponent av den totala energin i en enda kropp eftersom det inte är en tillståndsvariabel utan snarare en variabel som beskriver en överföring mellan två kroppar. Den adiabatiska processen är viktig eftersom den är en logisk ingrediens i denna nuvarande syn.

Olika användningar av ordet adiabatisk

Den här artikeln är skriven utifrån makroskopisk termodynamik, och ordet adiabatisk används i denna artikel på det traditionella sättet för termodynamik, introducerat av Rankine. Det påpekas i föreliggande artikel att om till exempel en komprimering av en gas är snabb, så finns det kort tid för värmeöverföring att ske, även när gasen inte är adiabatiskt isolerad av en bestämd vägg. I denna mening sägs en snabb komprimering av en gas ibland ungefär eller löst vara adiabatisk , men ofta långt ifrån isentropisk, även när gasen inte är adiabatiskt isolerad av en bestämd vägg.

Kvantmekanik och kvantstatistisk mekanik använder dock ordet adiabatisk i en helt annan betydelse , en som ibland kan verka nästan motsatt den klassiska termodynamiska betydelsen. I kvantteorin kan ordet adiabatiskt betyda något kanske nära isentropiskt, eller kanske nästan kvasistatiskt, men användningen av ordet är väldigt olika mellan de två disciplinerna.

Å ena sidan, i kvantteorin, om ett störande element av kompressionsarbete utförs nästan oändligt långsamt (det vill säga kvasi-statiskt), sägs det ha gjorts adiabatiskt . Tanken är att formerna på egenfunktionerna ändras långsamt och kontinuerligt, så att inget kvanthopp utlöses, och förändringen är praktiskt taget reversibel. Även om antalet yrkesgrupper är oförändrade, finns det ändå förändringar i energinivåerna för en-till-en motsvarande, före och efter kompression, egentillstånd. Sålunda har en störande del av arbetet utförts utan värmeöverföring och utan införande av slumpmässiga förändringar i systemet. Max Born skriver till exempel "Egentligen är det vanligtvis det 'adiabatiska' fallet som vi har att göra med: dvs det begränsande fallet där den yttre kraften (eller reaktionen av delarna i systemet på varandra) verkar mycket långsamt. I det här fallet till en mycket hög approximation

c_{1}^{2}=1,\,\,c_{2}^{2}=0,\,\,c_{3}^{2}=0,\,... \,,

det vill säga det finns ingen sannolikhet för en övergång, och systemet är i initialtillståndet efter att störningen upphört. En sådan långsam störning är därför reversibel, som den är klassiskt."

Å andra sidan, i kvantteorin, om ett störande element av kompressionsarbete utförs snabbt, ändrar det ockupationstalen och energierna för egentillstånden i proportion till övergångsmomentintegralen och i enlighet med tidsberoende störningsteori , samt stör den funktionella formen av själva egentillstånden. I den teorin sägs en sådan snabb förändring inte vara adiabatisk , och det motsatta ordet diabatisk tillämpas på den.

Ny forskning tyder på att kraften som absorberas från störningen motsvarar hastigheten för dessa icke-adiabatiska övergångar. Detta motsvarar den klassiska processen för energiöverföring i form av värme, men med de relativa tidsskalorna omvända i kvantfallet. Kvantadiabatiska processer sker över relativt långa tidsskalor, medan klassiska adiabatiska processer sker över relativt korta tidsskalor. Det bör också noteras att begreppet "värme" (med hänvisning till mängden värmeenergi som överförs) bryts ner på kvantnivå, och den specifika formen av energi (vanligtvis elektromagnetisk) måste övervägas istället. Den lilla eller försumbara absorptionen av energi från störningen i en kvantadiabatisk process ger en bra motivering för att identifiera den som kvantanalogen av adiabatiska processer i klassisk termodynamik, och för återanvändning av termen.

Vidare, inom atmosfärisk termodynamik, är en diabatisk process en process där värme utbyts.

Inom klassisk termodynamik skulle en sådan snabb förändring fortfarande kallas adiabatisk eftersom systemet är adiabatiskt isolerat, och det finns ingen överföring av energi som värme. Den starka irreversibiliteten av förändringen, på grund av viskositet eller annan entropiproduktion , påverkar inte denna klassiska användning.

För en gasmassa, i makroskopisk termodynamik, används ord så att en kompression ibland löst eller ungefärlig sägs vara adiabatisk om den är tillräckligt snabb för att undvika värmeöverföring, även om systemet inte är adiabatiskt isolerat. Men i kvantstatistisk teori kallas en komprimering inte adiabatisk om den är snabb, även om systemet är adiabatiskt isolerat i den klassiska termodynamiska betydelsen av termen. Orden används olika i de två disciplinerna, som nämnts ovan.

Se även

Relaterade fysikämnen

Relaterade termodynamiska processer

Allmän

Silbey, Robert J.; et al. (2004). Fysikalisk kemi . Hoboken: Wiley. sid. 55. ISBN 978-0-471-21504-2 .
Nave, Carl Rod. " Adiabatiska processer ". Hyperfysik.
Thorngren, Dr Jane R.. " Adiabatiska processer ". Daphne – A Palomar College Web Server., 21 juli 1995. Arkiverad 2011-05-09 på Wayback Machine .

externa länkar

Media relaterade till adiabatiska processer på Wikimedia Commons

Artikel i HyperPhysics Encyclopaedia