Elektriskt motstånd och konduktans

Det elektriska motståndet hos ett föremål är ett mått på dess motstånd mot flödet av elektrisk ström . Dess reciproka kvantitet är elektrisk konduktans , som mäter hur lätt en elektrisk ström passerar. Elektriskt motstånd delar några konceptuella paralleller med mekanisk friktion . SI - enheten för elektriskt motstånd är ohm ( $Ω$ ), medan elektrisk konduktans mäts i siemens (S) (tidigare kallad 'mho' och sedan representerad av $℧$ ).

Motståndet hos ett föremål beror till stor del på materialet det är gjort av. Föremål gjorda av elektriska isolatorer som gummi tenderar att ha mycket hög resistans och låg konduktans, medan föremål gjorda av elektriska ledare som metaller tenderar att ha mycket låg resistans och hög konduktans. Detta förhållande kvantifieras av resistivitet eller konduktivitet . Naturen hos ett material är dock inte den enda faktorn i resistans och konduktans; det beror också på storleken och formen på ett föremål eftersom dessa egenskaper är omfattande snarare än intensiva . Till exempel är en tråds motstånd högre om den är lång och tunn, och lägre om den är kort och tjock. Alla objekt motstår elektrisk ström, förutom supraledare , som har ett motstånd på noll.

Resistansen $R$ för ett objekt definieras som förhållandet mellan spänning $V$ över det och ström $I$ genom det, medan konduktansen $G$ är den reciproka:

R={\frac {V}{I}},\qquad G={\frac {I}{V}}={\frac {1

För en mängd olika material och förhållanden är $V$ och $I$ direkt proportionella mot varandra, och därför är $R$ och $G$ konstanter (även om de kommer att bero på föremålets storlek och form, materialet det är gjort av och andra faktorer som temperatur eller spänning ). Denna proportionalitet kallas Ohms lag och material som uppfyller den kallas ohmska material.

I andra fall, som en transformator , diod eller batteri , är $V$ och $I$ inte direkt proportionella. Förhållandet $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} V / I$ är ibland fortfarande användbart och kallas för ett kordamotstånd eller statiskt motstånd , eftersom det motsvarar den omvända lutningen av ett korda mellan origo och en $I$ - $V -$ kurva . I andra situationer kan derivatan ${\textstyle {\frac {\mathrm {d} V}{\mathrm {d} I}}}$ vara mest användbar; detta kallas differentialresistansen .

Introduktion

Den hydrauliska analogin jämför elektrisk ström som flyter genom kretsar med vatten som flyter genom rör. När ett rör (vänster) är fyllt med hår (höger) krävs ett större tryck för att uppnå samma vattenflöde. Att trycka elektrisk ström genom ett stort motstånd är som att trycka vatten genom ett rör som är igensatt med hår: Det krävs ett större tryck ( elektromotorisk kraft) för att driva samma flöde ( elektrisk ström ).

I den hydrauliska analogin är ström som flyter genom en tråd (eller motstånd ) som vatten som strömmar genom ett rör, och spänningsfallet över tråden är som tryckfallet som trycker vatten genom röret. Konduktansen är proportionell mot hur mycket flöde som sker för ett givet tryck, och motståndet är proportionellt mot hur mycket tryck som krävs för att uppnå ett givet flöde.

Spänningsfallet (dvs skillnaden mellan spänningar på ena sidan av motståndet och den andra), inte spänningen i sig , ger den drivande kraften som driver ström genom ett motstånd. I hydraulik är det liknande: tryckskillnaden mellan två sidor av ett rör, inte själva trycket, bestämmer flödet genom det. Det kan till exempel vara ett stort vattentryck ovanför röret, som försöker trycka ner vatten genom röret. Men det kan finnas ett lika stort vattentryck under röret, som försöker trycka tillbaka vatten upp genom röret. Om dessa tryck är lika, rinner inget vatten. (På bilden till höger är vattentrycket under röret noll.)

Resistansen och konduktansen hos en tråd, ett motstånd eller ett annat element bestäms mestadels av två egenskaper:

geometri (form), och
material

Geometri är viktig eftersom det är svårare att trycka vatten genom ett långt, smalt rör än ett brett, kort rör. På samma sätt har en lång, tunn koppartråd högre motstånd (lägre konduktans) än en kort, tjock koppartråd.

Material är också viktigt. Ett rör fyllt med hår begränsar vattenflödet mer än ett rent rör av samma form och storlek. På liknande sätt elektroner flöda fritt och lätt genom en koppartråd , men kan inte strömma lika lätt genom en ståltråd av samma form och storlek, och de kan i princip inte strömma alls genom en isolator som gummi , oavsett dess form. Skillnaden mellan koppar, stål och gummi är relaterad till deras mikroskopiska struktur och elektronkonfiguration , och kvantifieras av en egenskap som kallas resistivitet .

Förutom geometri och material finns det olika andra faktorer som påverkar resistans och konduktans, såsom temperatur; se nedan .

Ledare och motstånd

Ett 75 Ω motstånd , som identifieras av dess elektroniska färgkod (violett–grön–svart–guld–röd). En ohmmeter kan användas för att verifiera detta värde.

Ämnen som elektricitet kan flöda i kallas ledare . Ett stycke ledande material med en viss resistans avsedd för användning i en krets kallas ett motstånd . Ledare är gjorda av högkonduktiva material som metaller, speciellt koppar och aluminium. Resistorer, å andra sidan, är gjorda av en mängd olika material beroende på faktorer som önskat motstånd, mängd energi som den behöver för att försvinna, precision och kostnader.

Ohms lag

Ström -spänningsegenskaperna för fyra enheter: två motstånd , en diod och ett batteri . Den horisontella axeln är spänningsfall , den vertikala axeln är ström . Ohms lag är uppfylld när grafen är en rät linje genom origo. Därför är de två motstånden ohmska , men dioden och batteriet är det inte.

För många material är strömmen $I$ genom materialet proportionell mot spänningen $V$ som appliceras över det:

I\propto V

över ett brett spektrum av spänningar och strömmar. Därför är motståndet och konduktansen hos föremål eller elektroniska komponenter gjorda av dessa material konstant. Detta förhållande kallas Ohms lag , och material som lyder det kallas ohmska material. Exempel på ohmska komponenter är ledningar och motstånd . Ström -spänningsgrafen för en ohmsk enhet består av en rät linje genom origo med positiv lutning .

Andra komponenter och material som används i elektronik följer inte Ohms lag; strömmen är inte proportionell mot spänningen, så motståndet varierar med spänningen och strömmen genom dem. Dessa kallas olinjära eller icke-ohmiska . Exempel är dioder och lysrör . Ström-spänningskurvan för en icke-ohmsk enhet är en krökt linje.

Relation till resistivitet och konduktivitet

En bit resistivt material med elektriska kontakter i båda ändar.

Motståndet hos ett givet föremål beror främst på två faktorer: vilket material det är gjort av och dess form. För ett givet material är motståndet omvänt proportionellt mot tvärsnittsarean; till exempel har en tjock koppartråd lägre motstånd än en annars identisk tunn koppartråd. Även för ett givet material är motståndet proportionellt mot längden; till exempel har en lång koppartråd högre motstånd än en annars identisk kort koppartråd. Resistansen $R$ och konduktansen $G$ för en ledare med enhetligt tvärsnitt kan därför beräknas som

{\begin{aligned}R&=\rho {\frac {\ell }{A}},\\[5pt]G&=\sigma {\frac {A}{\ell }}\,.\end {Justerat}}

där $\ell$ är längden på ledaren, mätt i meter (m), $A$ är ledarens tvärsnittsarea mätt i kvadratmeter (m ² ), $σ$ ( sigma ) är den uppmätta elektriska ledningsförmågan i siemens per meter (S·m ⁻¹ ), och $ρ$ ( rho ) är den elektriska resistiviteten (även kallad specifik elektrisk resistans ) för materialet, mätt i ohm-meter (Ω·m). Resistiviteten och konduktiviteten är proportionalitetskonstanter och beror därför endast på materialet som tråden är gjord av, inte trådens geometri. Resistivitet och konduktivitet är reciproka : $\rho =1/\sigma$ . Resistivitet är ett mått på materialets förmåga att motverka elektrisk ström.

Denna formel är inte exakt, eftersom den antar att strömtätheten är helt enhetlig i ledaren, vilket inte alltid är sant i praktiska situationer. Denna formel ger dock fortfarande en bra uppskattning för långa tunna ledare som t.ex.

En annan situation för vilken denna formel inte är exakt är med växelström (AC), eftersom hudeffekten hämmar strömflödet nära mitten av ledaren. Av denna anledning skiljer sig det geometriska tvärsnittet från det effektiva tvärsnittet i vilket ström faktiskt flyter, så motståndet är högre än förväntat. På liknande sätt, om två ledare nära varandra bär växelström, ökar deras resistanser på grund av närhetseffekten . Vid kommersiell strömfrekvens är dessa effekter betydande för stora ledare som bär stora strömmar, såsom samlingsskenor i en elektrisk transformatorstation , eller stora kraftkablar som bär mer än några hundra ampere.

Resistiviteten hos olika material varierar enormt mycket: Till exempel är konduktiviteten hos teflon cirka 10 ³⁰ gånger lägre än kopparns ledningsförmåga. Löst sagt beror detta på att metaller har ett stort antal "delokaliserade" elektroner som inte sitter fast på någon plats, så de är fria att röra sig över stora avstånd. I en isolator, som teflon, är varje elektron tätt bunden till en enda molekyl så det krävs en stor kraft för att dra bort den. Halvledare ligger mellan dessa två ytterligheter. Mer information finns i artikeln: Elektrisk resistivitet och konduktivitet . För fallet med elektrolytlösningar , se artikeln: Konduktivitet (elektrolytisk) .

Resistiviteten varierar med temperaturen. I halvledare förändras resistiviteten också när de utsätts för ljus. Se nedan .

Mått

En ohmmeter

Ett instrument för att mäta resistans kallas ohmmeter . Enkla ohmmetrar kan inte mäta låga resistanser exakt eftersom resistansen hos deras mätledningar orsakar ett spänningsfall som stör mätningen, så mer exakta enheter använder fyrterminalsavkänning .

Typiska värden

Typiska motståndsvärden för valda objekt
Komponent	Motstånd (Ω)
1 meter koppartråd med 1 mm diameter	0,02
1 km luftledning ( typisk )	0,03
AA-batteri ( typiskt internt motstånd )	0,1
Glödlampa glödtråd ( typisk )	200–1000
Människokropp	1 000–100 000

Statiskt och differentiellt motstånd

Ström -spänningskurvan för en icke-ohmsk enhet (lila). Det statiska motståndet vid punkt A är den omvända lutningen av linje B genom origo. Differentialmotståndet vid A är den omvända lutningen av tangentlinjen C .

Ström -spänningskurvan för en komponent med negativt differentialresistans , ett ovanligt fenomen där ström-spänningskurvan är icke- montonisk .

Många elektriska element, såsom dioder och batterier , uppfyller inte Ohms lag . Dessa kallas icke-ohmiska eller icke-linjära , och deras ström-spänningskurvor är inte raka linjer genom origo.

Resistans och konduktans kan fortfarande definieras för icke-ohmiska element. Men till skillnad från ohmskt motstånd är det icke-linjära motståndet inte konstant utan varierar med spänningen eller strömmen genom enheten; dvs dess arbetspunkt . Det finns två typer av motstånd:

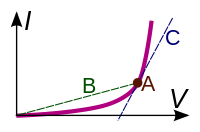
Statiskt motstånd: Detta motsvarar den vanliga definitionen av motstånd; spänningen dividerad med strömmen $R_{\mathrm {statisk} }={\frac {U}{I}}\,.$ Det är lutningen på linjen ( ackord ) från origo genom punkten på kurvan. Statiskt motstånd bestämmer effektförlusten i en elektrisk komponent. Punkter på ström-spänningskurvan i den 2:a eller 4:e kvadranten, för vilka ackordslinjens lutning är negativ, har negativ statisk resistans . Passiva enheter, som inte har någon energikälla, kan inte ha negativt statiskt motstånd. Men aktiva enheter som transistorer eller op-amps kan syntetisera negativt statiskt motstånd med feedback, och det används i vissa kretsar som gyratorer .
Differentialmotstånd: Differentialresistans är derivatan av spänningen med avseende på strömmen; lutningen för ström-spänningskurvan vid en punkt $R_{\mathrm {diff} }={\frac {{\mathrm {d} }U}{{\mathrm {d} }I}}\,.$ Om ström-spänningskurvan är icke monoton (med toppar och dalar), har kurvan en negativ lutning i vissa regioner - så i dessa regioner har enheten negativt differentialmotstånd . Enheter med negativt differentialmotstånd kan förstärka en signal som appliceras på dem och används för att göra förstärkare och oscillatorer. Dessa inkluderar tunneldioder , Gunn-dioder , IMPATT-dioder , magnetronrör och unijunction-transistorer .

AC-kretsar

Impedans och admittans

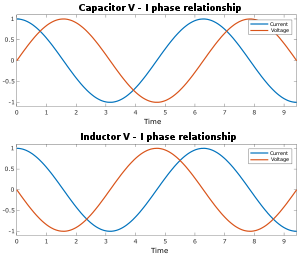
Spänningen (röd) och ström (blå) kontra tid (horisontell axel) för en kondensator (överst) och induktor (nederst). Eftersom amplituden för ström- och spänningssinusformerna är desamma är impedansens absoluta värde 1 för både kondensatorn och induktorn (i vilka enheter grafen än använder) . Å andra sidan är fasskillnaden mellan ström och spänning −90° för kondensatorn; därför är den komplexa fasen av kondensatorns impedans -90°. På liknande sätt är fasskillnaden mellan ström och spänning +90° för induktorn; därför är den komplexa fasen av induktorns impedans +90°.

När en växelström flyter genom en krets kännetecknas förhållandet mellan ström och spänning över ett kretselement inte bara av förhållandet mellan deras storlek, utan också av skillnaden i deras faser . Till exempel, i ett idealiskt motstånd , det ögonblick när spänningen når sitt maximum, når strömmen också sitt maximum (ström och spänning oscillerar i fas). Men för en kondensator eller induktor uppstår det maximala strömflödet när spänningen passerar genom noll och vice versa (ström och spänning oscillerar 90° ur fas, se bilden nedan). Komplexa tal används för att hålla reda på både fasen och storleken på ström och spänning:

{\begin{array}{cl}u(t)&=\operatörsnamn {\mathcal {R_{e}}} \left(U_{0}\cdot e^{j\omega t}\right)\\i (t)&=\operatörsnamn {\mathcal {R_{e}}} \left(I_{0}\cdot e^{j(\omega t+\varphi )}\right)\\Z&={\frac {U }{\ I\ }}\\Y&={\frac {\ 1\ }{Z}}={\frac {\ I\ }{U}}\end{array}}

var:

$t$ är tid;
$u (t)$ och $i (t)$ är spänningen respektive strömmen som funktion av tiden;
$U 0$ och $I 0$ anger amplituden för spänningen respektive strömmen;
$\omega$ är vinkelfrekvensen för AC-strömmen;
$\varphi$ är förskjutningsvinkeln;
$U$ och $I$ är den komplext värderade spänningen respektive strömmen;
$Z$ och $Y$ är den komplexa impedansen respektive admittansen ;
${\mathcal {R_{e}}}$ indikerar den reella delen av ett komplext tal ; och
$j\equiv {\sqrt {-1\ }}$ är den imaginära enheten .

Impedansen och admittansen kan uttryckas som komplexa tal som kan delas upp i reella och imaginära delar:

{\begin{aligned}Z&=R+jX\\Y&=G+jB~.\end{aligned}}

där $R$ är resistans, $G$ är konduktans, $X$ är reaktans och $B$ är susceptans . Dessa leder till de komplexa nummeridentiteterna

{\begin{aligned}R&={ \frac {G}{\ G^{2}+B^{2}\ }}\ ,\qquad &X={\frac {-B~}{\ G^{2}+B^{2}\ } }\ ,\\G&={\frac {R}{\ R^{2}+X^{2}\ }}\ ,\qquad &B={\frac {-X~}{\ R^{2} +X^{2}\ }}\ ,\end{aligned}}

som är sanna i alla fall, medan

\ R=1/G\

endast är sant i de speciella fallen av antingen DC eller reaktansfri ström.

Den komplexa vinkeln $\ \theta =\arg(Z)=-\arg(Y)\$ är fasskillnaden mellan spänningen och strömmen som passerar genom en komponent med impedans $Z$ . För kondensatorer och induktorer är denna vinkel exakt -90° respektive +90°, och $X$ och $B$ är icke noll. Idealiska motstånd har en vinkel på 0°, eftersom $X$ är noll (och därmed B $också$ ), och $Z$ och $Y$ reduceras till $R$ respektive $G.$ I allmänhet är AC-system utformade för att hålla fasvinkeln nära 0° så mycket som möjligt, eftersom det minskar den reaktiva effekten , vilket inte gör något användbart arbete vid en belastning. I ett enkelt fall med en induktiv belastning (som får fasen att öka), kan en kondensator läggas till för kompensation vid en frekvens, eftersom kondensatorns fasförskjutning är negativ, vilket för den totala impedansfasen närmare 0° igen.

$Y$ är den reciproka av $Z$ ( $\ Z=1/Y\$ ) för alla kretsar, precis som $R=1/G$ för DC-kretsar som endast innehåller motstånd , eller AC-kretsar för vilka antingen reaktansen eller susceptansen råkar vara noll ( $X$ eller $B = 0 ,$ respektive) (om en är noll, då för realistiska system måste båda vara noll).

Frekvensberoende

En nyckelfunktion hos AC-kretsar är att resistansen och konduktansen kan vara frekvensberoende, ett fenomen som kallas det universella dielektriska svaret . En orsak som nämns ovan är hudeffekten (och den relaterade närhetseffekten ). En annan anledning är att resistiviteten i sig kan bero på frekvens (se Drude-modellen , djupnivåfällor , resonansfrekvens , Kramers–Kronig-relationer , etc.)

Energiavledning och Joule-uppvärmning

Att köra ström genom ett material med motstånd skapar värme, i ett fenomen som kallas Joule-uppvärmning . På den här bilden lyser en patronvärmare , uppvärmd av Joule-uppvärmning, glödhet .

Motstånd (och andra element med motstånd) motsätter sig flödet av elektrisk ström; därför krävs elektrisk energi för att driva ström genom motståndet. Denna elektriska energi försvinner och värmer upp motståndet i processen. Detta kallas Joule-uppvärmning (efter James Prescott Joule ), även kallad ohmsk uppvärmning eller resistiv uppvärmning .

Förlusten av elektrisk energi är ofta oönskad, särskilt i fallet med överföringsförluster i kraftledningar . Högspänningsöverföring hjälper till att minska förlusterna genom att minska strömmen för en given effekt.

Å andra sidan är Joule-uppvärmning ibland användbar, till exempel i elektriska spisar och andra elektriska värmare (även kallade resistiva värmare ). Som ett annat exempel glödlampor på Joule-uppvärmning: glödtråden värms upp till en så hög temperatur att den lyser "vitvarm" med termisk strålning (även kallad glödlampa ).

Formeln för Joule-uppvärmning är:

P=I^{2}R

där

P

är effekten (energi per tidsenhet) omvandlad från elektrisk energi till termisk energi,

R

är resistansen och

I

är strömmen genom motståndet.

Beroende av andra förutsättningar

Temperaturberoende

Nära rumstemperatur ökar resistiviteten hos metaller vanligtvis när temperaturen höjs, medan resistiviteten hos halvledare vanligtvis minskar när temperaturen höjs. Resistiviteten hos isolatorer och elektrolyter kan öka eller minska beroende på systemet. För detaljerat beteende och förklaring, se Elektrisk resistivitet och konduktivitet .

Som en konsekvens ändras ofta motståndet hos ledningar, motstånd och andra komponenter med temperaturen. Denna effekt kan vara oönskad, vilket gör att en elektronisk krets inte fungerar vid extrema temperaturer. I vissa fall kommer effekten dock till god användning. När temperaturberoende resistans hos en komponent används målmedvetet kallas komponenten en resistanstermometer eller termistor . (En motståndstermometer är gjord av metall, vanligtvis platina, medan en termistor är gjord av keramik eller polymer.)

Motståndstermometrar och termistorer används vanligtvis på två sätt. För det första kan de användas som termometrar : genom att mäta motståndet kan man sluta sig till omgivningens temperatur. För det andra kan de användas i samband med Joule-uppvärmning (även kallad självuppvärmning): om det går en stor ström genom motståndet, stiger motståndets temperatur och därför ändras dess motstånd. Därför kan dessa komponenter användas i en kretsskyddande roll som liknar säkringar , eller för återkoppling i kretsar, eller för många andra ändamål. I allmänhet kan självuppvärmning förvandla ett motstånd till ett olinjärt och hysteretiskt kretselement. För mer information se Thermistor#Självuppvärmningseffekter .

Om temperaturen $T$ inte varierar för mycket, används vanligtvis en linjär approximation :

R(T)=R_{0}[1+\alpha (T-T_{0})]

där

\alpha

kallas motståndets temperaturkoefficient ,

T_{0}

är en fast referenstemperatur (vanligtvis rumstemperatur), och

R_{0}

är resistansen vid temperatur

T_{0}

. Parametern

\alpha

är en empirisk parameter anpassad från mätdata. Eftersom den linjära approximationen endast är en approximation,

\alpha

olika för olika referenstemperaturer. Av denna anledning är det vanligt att specificera temperaturen som

\alpha

uppmättes vid med ett suffix, såsom

\alpha _{15}

, och förhållandet gäller endast inom ett temperaturintervall runt referensen.

Temperaturkoefficienten $\alpha$ är typiskt +3 × 10 ⁻³ K−1 till +6 × 10 ⁻³ K−1 för metaller nära rumstemperatur. Det är vanligtvis negativt för halvledare och isolatorer, med mycket varierande storlek.

Stamberoende

Precis som en ledares resistans beror på temperatur, beror resistansen hos en ledare på töjning . Genom att sätta en ledare under spänning (en form av spänning som leder till töjning i form av sträckning av ledaren), ökar längden på den ledare som är under spänning och dess tvärsnittsarea minskar. Båda dessa effekter bidrar till att öka motståndet hos den ansträngda ledarens del. Under kompression (töjning i motsatt riktning) minskar motståndet hos den spända sektionen av ledaren. Se diskussionen om töjningsmätare för detaljer om enheter konstruerade för att dra fördel av denna effekt.

Beroende av ljusbelysning

Vissa motstånd, särskilt de som är gjorda av halvledare , uppvisar fotokonduktivitet , vilket betyder att deras motstånd ändras när ljus lyser på dem. Därför kallas de fotoresistorer (eller ljusberoende motstånd ). Dessa är en vanlig typ av ljusdetektorer .

Superledningsförmåga

Supraledare är material som har exakt noll resistans och oändlig konduktans, eftersom de kan ha $V = 0$ och $I \neq 0$ . Detta betyder också att det inte finns någon jouleuppvärmning , eller med andra ord ingen förlust av elektrisk energi. Därför, om supraledande tråd görs till en sluten slinga, flyter ström runt slingan för alltid. Supraledare kräver kylning till temperaturer nära 4 K med flytande helium för de flesta metalliska supraledare som niob- tennlegeringar, eller kylning till temperaturer nära 77 K med flytande kväve för dyra, spröda och känsliga keramiska högtemperatursupraledare . Ändå finns det många tekniska tillämpningar av supraledning, inklusive supraledande magneter .

Se även

Konduktans kvant
- Von Klitzing konstant (dess ömsesidiga)
Elektriska mätningar
Kontaktmotstånd
Elektrisk resistivitet och konduktivitet för mer information om de fysiska mekanismerna för ledning i material.
Johnson–Nyquist brus
Quantum Hall-effekt , en standard för högnoggranna motståndsmätningar.
Motstånd
RKM-kod
Serie- och parallellkretsar
Plåtmotstånd
SI elektromagnetism enheter
Termisk resistans
Spänningsdelare
Spänningsfall

Fotnoter

externa länkar

"Motståndskalkylator" . Fordonselektroniklaboratoriet. Clemson University. Arkiverad från originalet den 11 juli 2010.
"Elektronkonduktansmodeller som använder maximal entropi slumpmässiga promenader" . wolfram.com . Wolfram demonstrationsprojekt.