Väteatom
 | |
| Allmän | |
|---|---|
| Symbol | 1 H |
| Namn |
väteatom, IH, H-1, protium |
| Protoner ( Z ) | 1 |
| Neutroner ( N ) | 0 |
| Nukliddata | |
| Naturligt överflöd | 99,985 % |
| Halveringstid ( t 1/2 ) | stabil |
| Isotopmassa | 1,007825 Da |
| Snurra | 1/2 _ _ |
| Överskott av energi | 7 288 , 969 ± 0,001 keV |
| Bindande energi | 0,000 ± 0,0000 keV |
|
Isotoper av väte Fullständig tabell över nuklider | |
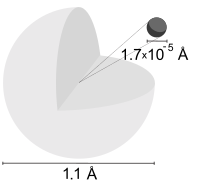
En väteatom är en atom av det kemiska elementet väte . Den elektriskt neutrala atomen innehåller en enda positivt laddad proton och en enda negativt laddad elektron bundna till kärnan av Coulomb-kraften . Atomiskt väte utgör cirka 75 % av universums baryonmassa .
I vardagslivet på jorden är isolerade väteatomer (kallade "atomärt väte") extremt sällsynta. Istället tenderar en väteatom att kombineras med andra atomer i föreningar, eller med en annan väteatom för att bilda vanlig ( diatomisk ) vätgas, H 2 . "Atomic hydrogen" och "väteatom" i vanlig engelsk användning har överlappande, men ändå distinkta, betydelser. Till exempel innehåller en vattenmolekyl två väteatomer, men innehåller inte atomärt väte (vilket skulle hänvisa till isolerade väteatomer).
Atomspektroskopi visar att det finns en diskret oändlig uppsättning tillstånd där en väteatom (eller vilken som helst) atom kan existera, i motsats till klassisk fysiks förutsägelser . Försök att utveckla en teoretisk förståelse av väteatomens tillstånd har varit viktiga för kvantmekanikens historia, eftersom alla andra atomer grovt kan förstås genom att veta i detalj om denna enklaste atomstruktur.
Isotoper
Den vanligaste isotopen , väte -1 , protium eller lätt väte , innehåller inga neutroner och är helt enkelt en proton och en elektron . Protium är stabilt och utgör 99,985 % av naturligt förekommande väteatomer.
Deuterium ( 2H ) innehåller en neutron och en proton i sin kärna. Deuterium är stabilt och utgör 0,0156 % av naturligt förekommande väte och används i industriella processer som kärnreaktorer och kärnmagnetisk resonans .
Tritium ( 3 H ) innehåller två neutroner och en proton i sin kärna och är inte stabil, sönderfaller med en halveringstid på 12,32 år. På grund av dess korta halveringstid finns tritium inte i naturen förutom i spårmängder.
Tyngre isotoper av väte skapas endast artificiellt i partikelacceleratorer och har halveringstider i storleksordningen 10–22 sekunder . De är obundna resonanser placerade bortom neutrondropplinjen ; detta resulterar i omedelbar emission av en neutron .
Formlerna nedan är giltiga för alla tre isotoper av väte, men något olika värden på Rydberg-konstanten (korrigeringsformel ges nedan) måste användas för varje väteisotop.
Vätejon
Ensamma neutrala väteatomer är sällsynta under normala förhållanden. Emellertid är neutralt väte vanligt när det är kovalent bundet till en annan atom, och väteatomer kan också existera i katjoniska och anjoniska former.
Om en neutral väteatom förlorar sin elektron blir den en katjon. Den resulterande jonen, som enbart består av en proton för den vanliga isotopen, skrivs som "H + " och kallas ibland hydron . Fria protoner är vanliga i det interstellära mediet och i solvinden . I samband med vattenlösningar av klassiska Brønsted–Lowry-syror , såsom saltsyra , är det egentligen hydronium , H 3 O + , som avses. Istället för att en bokstavlig joniserad enkel väteatom bildas överför syran vätet till H 2 O och bildar H 3 O + .
Om istället en väteatom får en andra elektron blir den en anjon. Väteanjonen skrivs som "H - " och kallas hydrid .
Teoretisk analys
Väteatomen har särskild betydelse inom kvantmekanik och kvantfältteori som ett enkelt fysiskt system för tvåkroppsproblem som har gett många enkla analytiska lösningar i sluten form.
Misslyckad klassisk beskrivning
Experiment av Ernest Rutherford 1909 visade att atomens struktur var en tät, positiv kärna med ett svagt negativt laddningsmoln runt sig. Detta väckte omedelbart frågor om hur ett sådant system skulle kunna vara stabilt. Klassisk elektromagnetism hade visat att varje accelererande laddning utstrålar energi, vilket framgår av Larmor-formeln . Om elektronen antas kretsa i en perfekt cirkel och utstrålar energi kontinuerligt, skulle elektronen snabbt spiralera in i kärnan med en falltid på:
Bohr–Sommerfeld modell
År 1913 erhöll Niels Bohr väteatomens energinivåer och spektrala frekvenser efter att ha gjort ett antal enkla antaganden för att rätta till den misslyckade klassiska modellen. Antagandena inkluderade:
- Elektroner kan bara vara i vissa, diskreta cirkulära banor eller stationära tillstånd , och därigenom ha en diskret uppsättning möjliga radier och energier.
- Elektroner avger inte strålning när de befinner sig i ett av dessa stationära tillstånd.
- En elektron kan få eller förlora energi genom att hoppa från en diskret bana till en annan.
Bohr antog att elektronens rörelsemängd kvantiseras med möjliga värden:
För , värdet
Det exakta värdet på Rydbergskonstanten antar att kärnan är oändligt massiv med avseende på elektronen. För väte-1, väte-2 ( deuterium ) och väte-3 ( tritium ) som har ändlig massa, måste konstanten modifieras något för att använda den reducerade massan av systemet, snarare än bara elektronens massa. Detta inkluderar den kinetiska energin för kärnan i problemet, eftersom den totala (elektron plus kärn) kinetiska energin är ekvivalent med den kinetiska energin för den reducerade massan som rör sig med en hastighet lika med elektronhastigheten i förhållande till kärnan. Men eftersom kärnan är mycket tyngre än elektronen, är elektronmassan och reducerad massa nästan densamma. Rydberg-konstanten R M för en väteatom (en elektron), R ges av
Det fanns fortfarande problem med Bohrs modell:
- den misslyckades med att förutsäga andra spektrala detaljer såsom fin struktur och hyperfin struktur
- den kunde bara förutsäga energinivåer med någon noggrannhet för enelektronatomer (väteliknande atomer)
- de förutsagda värdena var endast korrekta till där är finstrukturkonstanten .
De flesta av dessa brister löstes genom Arnold Sommerfelds modifiering av Bohr-modellen. Sommerfeld introducerade ytterligare två frihetsgrader, vilket gjorde det möjligt för en elektron att röra sig på en elliptisk bana som kännetecknas av dess excentricitet och deklination med avseende på en vald axel. Detta introducerade ytterligare två kvanttal, som motsvarar rörelsemängden i omloppsbanan och dess projektion på den valda axeln. Således hittades den korrekta mångfalden av tillstånd (förutom faktorn 2 som står för det ännu okända elektronspinnet). Vidare, genom att tillämpa speciell relativitet på de elliptiska banorna, lyckades Sommerfeld härleda det korrekta uttrycket för den fina strukturen av vätespektra (vilket råkar vara exakt samma som i den mest utarbetade Dirac-teorin). Men några observerade fenomen, såsom den anomala Zeeman-effekten , förblev oförklarade. Dessa problem löstes med den fulla utvecklingen av kvantmekaniken och Dirac-ekvationen . Det påstås ofta att Schrödinger-ekvationen är överlägsen Bohr-Sommerfeld-teorin när det gäller att beskriva en väteatom. Detta är inte fallet, eftersom de flesta av resultaten av båda tillvägagångssätten sammanfaller eller är mycket nära (ett anmärkningsvärt undantag är problemet med väteatomer i korsade elektriska och magnetiska fält, som inte kan lösas självständigt inom ramen för Bohr– Sommerfeld-teorin), och i båda teorierna beror de största bristerna på frånvaron av elektronspin. Det var det fullständiga misslyckandet med Bohr-Sommerfeld-teorin att förklara många-elektronsystem (som heliumatom eller vätemolekyl) som visade dess otillräcklighet i att beskriva kvantfenomen.
Schrödinger ekvation
Schrödinger-ekvationen tillåter en att beräkna de stationära tillstånden och även tidsutvecklingen för kvantsystem. Exakta analytiska svar finns tillgängliga för den icke-relativistiska väteatomen. Innan vi går till att presentera en formell redogörelse ger vi här en elementär översikt.
Med tanke på att väteatomen innehåller en kärna och en elektron, tillåter kvantmekaniken att förutsäga sannolikheten att hitta elektronen på ett givet radiellt avstånd r {\ . Den ges av kvadraten på en matematisk funktion känd som "vågfunktionen", som är en lösning av Schrödinger-ekvationen. Väteatomens lägsta energijämviktstillstånd är känt som grundtillståndet. Marktillståndsvågfunktionen är känd som vågfunktionen. Det är skrivet som:
Här är det numeriska värdet för Bohr-radien. Sannolikhetstätheten för att hitta elektronen på ett avstånd i valfri radiell riktning är det kvadratiska värdet på vågfunktionen:
1 vågfunktionen är sfäriskt symmetrisk, och ytarean på ett skal på avstånd är , så den totala sannolikheten för att elektronen är i ett skal på ett avstånd och tjockleken är
Det visar sig att detta är ett maximum vid . Det vill säga, Bohr-bilden av en elektron som kretsar kring kärnan vid radie motsvarar den mest sannolika radien. Egentligen finns det en ändlig sannolikhet att elektronen kan hittas var som helst , med sannolikheten indikerad av kvadraten på vågfunktionen. Eftersom sannolikheten för att hitta elektronen någonstans i hela volymen är enhet, är integralen av enhet. Då säger vi att vågfunktionen är ordentligt normaliserad.
indikeras grundtillståndet kvanttalen . De näst lägsta energitillstånden, strax ovanför marktillståndet, ges av kvanttalen , , och . Dessa tillstånd har alla samma energi och kallas tillstånden 2 och Det finns ett tillstånd:
En elektron i tillståndet eller finns mest sannolikt i den andra Bohr-banan med energi som ges av Bohr-formeln.
Vågfunktion
Väteatomens Hamiltonian är den radiella kinetiska energioperatorn och Coulomb-attraktionskraften mellan den positiva protonen och den negativa elektronen . Genom att använda den tidsoberoende Schrödinger-ekvationen, ignorera alla spinnkopplingsinteraktioner och använda den reducerade massan , skrivs ekvationen som:
Expandera Laplacian i sfäriska koordinater:
Detta är en separerbar , partiell differentialekvation som kan lösas i termer av speciella funktioner. När vågfunktionen separeras som produkt av funktionerna , och tre oberoende differentialfunktioner visas med A och B som separationskonstanterna:
- radiell:
- polär:
- azimut:
De normaliserade positionsvågfunktionerna , angivna i sfäriska koordinater är:
var:
- ,
- är den reducerade Bohr-radien , ,
- är ett generaliserat Laguerrepolynom av grad , och
- är en sfärisk harmonisk funktion av graden och ordningen . Observera att de generaliserade Laguerre-polynomen definieras olika av olika författare. Användningen här överensstämmer med definitionerna som används av Messias och Mathematica. På andra ställen inkluderar Laguerre-polynomet en faktor på , eller det generaliserade Laguerre-polynomet som förekommer i vätevågsfunktionen är istället.
Kvanttalen kan ha följande värden:
- ( huvudkvanttal )
- ( azimutalt kvantnummer )
- ( magnetiskt kvanttal) .
Dessutom är dessa vågfunktioner normaliserade (dvs. integralen av deras modulkvadrat är lika med 1) och ortogonala :
Vågfunktionerna i momentumrymden är relaterade till vågfunktionerna i positionsrymden genom en Fouriertransform
Lösningarna till Schrödinger-ekvationen för väte är analytiska , vilket ger ett enkelt uttryck för väteenerginivåerna och därmed frekvenserna för vätespektrallinjerna och reproducerade Bohr-modellen helt och gick utöver den. Det ger också två andra kvanttal och formen på elektronens vågfunktion ("orbital") för de olika möjliga kvantmekaniska tillstånden, vilket förklarar den anisotropa karaktären hos atombindningar.
Schrödinger-ekvationen gäller även för mer komplicerade atomer och molekyler . När det finns mer än en elektron eller kärna är lösningen inte analytisk och antingen krävs datorberäkningar eller så måste förenklade antaganden göras.
Eftersom Schrödinger-ekvationen endast är giltig för icke-relativistisk kvantmekanik, är lösningarna den ger för väteatomen inte helt korrekta. Dirac -ekvationen för relativistisk kvantteori förbättrar dessa lösningar (se nedan).
Resultat av Schrödinger-ekvationen
Lösningen av Schrödinger-ekvationen (vågekvationen) för väteatomen använder det faktum att Coulomb-potentialen som produceras av kärnan är isotrop (den är radiellt symmetrisk i rymden och beror bara på avståndet till kärnan). Även om de resulterande energiegenfunktionerna (orbitalerna ) inte nödvändigtvis är isotropa själva , följer deras beroende av vinkelkoordinaterna helt generellt från denna isotropi av den underliggande potentialen: Hamiltonianens egentillstånd ( det vill säga energiegentillstånden) kan väljas som samtidiga egentillstånd för rörelsemängdsoperatorn . Detta motsvarar det faktum att rörelsemängd bevaras i elektronens omloppsrörelse runt kärnan. Därför kan energiegentillstånden klassificeras av två vinkelmomentumkvanttal , ℓ { och (båda är heltal). Vinkelmomentets kvanttal bestämmer storleken på rörelsemängden. Det magnetiska kvanttalet bestämmer projektionen av rörelsemängden på den (godtyckligt valda) -axeln .
Förutom matematiska uttryck för total rörelsemängd och rörelsemängdsprojektion av vågfunktioner måste ett uttryck för vågfunktionernas radiella beroende hittas. Det är bara här som detaljerna för Coulomb-potentialen kommer in (som leder till Laguerre-polynom i ). Detta leder till ett tredje kvanttal, det huvudsakliga kvanttalet . Det huvudsakliga kvanttalet i väte är relaterat till atomens totala energi.
Observera att det maximala värdet för kvanttalet för vinkelmomentet begränsas av det huvudsakliga kvanttalet: det kan endast löpa upp till dvs. .
På grund av bevarande av vinkelmomentum har tillstånd med samma men olika samma energi (detta gäller för alla problem med rotationssymmetri ). Dessutom, för väteatomen, är tillstånd med samma men olika också degenererade (dvs. de har samma energi). Detta är dock en specifik egenskap hos väte och gäller inte längre för mer komplicerade atomer som har en (effektiv) potential som skiljer sig från formen (på grund av närvaron av de inre elektronerna som skärmar kärnpotential).
Om man tar hänsyn till elektronens spin adderas ett sista kvanttal, projektionen av elektronens spin vinkelmomentum längs -axeln, som kan anta två värden. Därför beskrivs varje egentillstånd för elektronen i väteatomen fullständigt av fyra kvanttal. Enligt kvantmekanikens vanliga regler kan elektronens faktiska tillstånd vara vilken som helst överlagring av dessa tillstånd. Detta förklarar också varför valet av -axeln för riktningskvantiseringen av rörelsemängdsvektorn är oväsentligt: en orbital med given och erhållen för en annan föredragen axel kan alltid representeras som en lämplig överlagring av de olika tillstånden för olika (men samma som har erhållits för .
Matematisk sammanfattning av egentillstånd för väteatomer
1928 hittade Paul Dirac en ekvation som var helt kompatibel med speciell relativitet , och (som en konsekvens) gjorde vågfunktionen till en 4-komponent " Dirac spinor " inklusive "upp" och "ner" spin komponenter, med både positiva och " negativ" energi (eller materia och antimateria). Lösningen till denna ekvation gav följande resultat, mer exakt än Schrödinger-lösningen.
Energinivåer
Energinivåerna för väte, inklusive finstruktur (exklusive Lamb shift och hyperfin struktur ), ges av Sommerfelds finstrukturuttryck :
Sammanhängande stater
De sammanhängande staterna har föreslagits som
Visualisera väteelektronens orbitaler
Bilden till höger visar de första väteatomernas orbitaler (energiegenfunktioner). Dessa är tvärsnitt av sannolikhetstätheten som är färgkodade (svart representerar noll densitet och vitt representerar den högsta densiteten). Vinkelmomentet (orbital) kvantnumret ℓ anges i varje kolumn, med den vanliga spektroskopiska bokstavskoden ( s betyder ℓ = 0, p betyder ℓ = 1, d betyder ℓ = 2). Huvudkvanttalet n (= 1, 2, 3, ...) är markerat till höger om varje rad. För alla bilder har det magnetiska kvanttalet m satts till 0, och tvärsnittsplanet är xz -planet ( z är den vertikala axeln). Sannolikhetstätheten i tredimensionellt utrymme erhålls genom att vrida den som visas här runt z -axeln.
" Grundtillståndet ", dvs tillståndet med lägst energi, i vilket elektronen vanligtvis finns, är det första, 1 s- tillståndet ( huvudkvantnivå n = 1, ℓ = 0).
Svarta linjer förekommer i var och en utom den första omloppsbanan: dessa är noderna för vågfunktionen, dvs där sannolikhetstätheten är noll. (Närmare bestämt är noderna sfäriska övertoner som uppstår som ett resultat av att lösa Schrödinger-ekvationen i sfäriska koordinater.)
Kvanttalen bestämmer layouten för dessa noder . Det finns:
- totala noder,
-
varav är vinkelnoder:
- vinkelnoder går runt -axeln (i xy -planet). (Figuren ovan visar inte dessa noder eftersom den plottar tvärsnitt genom xz -planet.)
- (de återstående vinkelnoderna) förekommer på (vertikal) axeln.
- (de återstående icke-vinkelnoderna) är radiella noder.
Funktioner som går utöver Schrödinger-lösningen
Det finns flera viktiga effekter som försummas av Schrödinger-ekvationen och som är ansvariga för vissa små men mätbara avvikelser av de verkliga spektrallinjerna från de förutsagda:
- Även om medelhastigheten för elektronen i väte bara är 1/137 av ljusets hastighet , är många moderna experiment tillräckligt exakta för att en fullständig teoretisk förklaring kräver en helt relativistisk behandling av problemet. En relativistisk behandling resulterar i en momentumökning på cirka 1 del av 37 000 för elektronen. Eftersom elektronens våglängd bestäms av dess rörelsemängd, visar orbitaler som innehåller elektroner med högre hastighet sammandragning på grund av mindre våglängder.
- Även när det inte finns något externt magnetfält , i den rörliga elektronens tröghetsram , har kärnans elektromagnetiska fält en magnetisk komponent. Elektronens spinn har ett tillhörande magnetiskt moment som interagerar med detta magnetfält. Denna effekt förklaras också av speciell relativitet, och den leder till den så kallade spin-omloppskopplingen , dvs en interaktion mellan elektronens omloppsrörelse runt kärnan och dess spin .
Båda dessa funktioner (och fler) ingår i den relativistiska Dirac-ekvationen , med förutsägelser som kommer ännu närmare experiment. Återigen kan Dirac-ekvationen lösas analytiskt i det speciella fallet med ett tvåkroppssystem, såsom väteatomen. De resulterande lösningskvanttillstånden måste nu klassificeras efter det totala rörelsemängdsmängdstalet j (som uppstår genom kopplingen mellan elektronspin och orbital rörelsemängd ). Tillstånd av samma j och samma n är fortfarande degenererade. Således förutsäger direkt analytisk lösning av 1/2 att Dirac -ekvationen 2S( 1/2 Lam - ) och 2P( ) nivåer av väte har exakt samma energi, vilket står i motsägelse till observationer ( Retherford-experiment ).
- Det finns alltid vakuumfluktuationer i det elektromagnetiska fältet , enligt kvantmekaniken. På grund av sådana fluktuationer lyfts degeneration mellan tillstånd av samma j men olika l , vilket ger dem något olika energier. Detta har visats i det berömda Lamb–Retherford-experimentet och var startpunkten för utvecklingen av teorin om kvantelektrodynamik (som kan hantera dessa vakuumfluktuationer och använder de berömda Feynman-diagrammen för approximationer med hjälp av störningsteori ). Denna effekt kallas nu för Lamb shift .
För dessa utvecklingar var det väsentligt att lösningen av Dirac-ekvationen för väteatomen kunde utarbetas exakt, så att varje experimentellt observerad avvikelse måste tas på allvar som en signal om att teorin misslyckats.
Alternativ till Schrödinger-teorin
På språket i Heisenbergs matrismekanik löstes väteatomen först av Wolfgang Pauli med en rotationssymmetri i fyra dimensioner [O(4)-symmetri] genererad av rörelsemängden och Laplace-Runge-Lenz-vektorn . Genom att utöka symmetrigruppen O(4) till den dynamiska gruppen O(4,2) inbäddades hela spektrumet och alla övergångar i en enda irreducerbar grupprepresentation.
1979 löstes den (icke-relativistiska) väteatomen för första gången inom Feynmans vägintegralformulering av kvantmekanik av Duru och Kleinert. Detta arbete utökade avsevärt tillämpningsområdet för Feynmans metod.
Se även
Böcker
- Griffiths, David J. (1995). Introduktion till kvantmekanik . Prentice Hall . ISBN 0-13-111892-7 . Avsnitt 4.2 behandlar väteatomen specifikt, men hela kapitel 4 är relevant.
- Kleinert, H. (2009). Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 4:e upplagan, Worldscibooks.com , World Scientific, Singapore (även tillgänglig online physik.fu-berlin.de )
externa länkar










































![{\displaystyle -{\frac {\hbar ^{2}}{2\mu }}\left[{\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial \psi }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}\psi }{\partial \varphi ^{2}}}\right]-{\frac {e^{2}}{4\pi \varepsilon _{0}r}}\psi =E\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fed150abb1693ab2493937b669446a54865b9562)







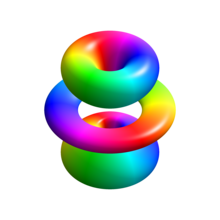






























![{\displaystyle {\begin{aligned}E_{j\,n}={}&-\mu c^{2}\left[1-\left(1+\left[{\frac {\alpha }{n-j-{\frac {1}{2}}+{\sqrt {\left(j+{\frac {1}{2}}\right)^{2}-\alpha ^{2}}}}}\right]^{2}\right)^{-1/2}\right]\\\approx {}&-{\frac {\mu c^{2}\alpha ^{2}}{2n^{2}}}\left[1+{\frac {\alpha ^{2}}{n^{2}}}\left({\frac {n}{j+{\frac {1}{2}}}}-{\frac {3}{4}}\right)\right],\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e54f0064eafaeab9e7d8b3e5e41e667a3138a7b)




![{\displaystyle {\begin{aligned}\langle r,\theta ,\varphi \mid s,\gamma ,{\bar {\Omega }}\rangle ={}&e^{-s^{2}/2}\sum _{n=0}^{\infty }(s^{n}e^{i\gamma /(n+1)^{2}}/{\sqrt {n!}})\\&{}\times \,\sum _{\ell =0}^{n}u_{n+1}^{\ell }(r)\sum _{m=-\ell }^{\ell }\left[{\frac {(2\ell )!}{(\ell +m)!(\ell -m)!}}\right]^{1/2}\left(\sin {\frac {\bar {\theta }}{2}}\right)^{\ell -m}\left(\cos {\frac {\bar {\theta }}{2}}\right)^{\ell +m}\\&{}\times \,e^{-i(m{\bar {\varphi }}+\ell {\bar {\psi }})}Y_{\ell m}(\theta ,\varphi ){\sqrt {2\ell +1}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb48ff266b61e92b9bdfcd39d562729c3910e97a)



