Tvåkroppsproblem

Den här artikeln handlar om tvåkroppsproblemet i klassisk mekanik. För den relativistiska versionen, se Tvåkroppsproblem i allmän relativitet . För karriärhanteringsproblemet för arbetande par, se Tvåkroppsproblem (karriär) .

Vänster: Två kroppar med liknande massa som kretsar kring ett gemensamt barycentrum utanför båda kropparna, med elliptiska banor — typiska för dubbelstjärnor . Till höger: Två kroppar med en "liten" skillnad i massa som kretsar kring ett gemensamt barycentrum. Storlekarna och denna typ av omloppsbana liknar Pluto-Charon-systemet (där barycentret är externt till båda kropparna), och jorden - månsystemet - där barycentret är internt i den större kroppen.

I klassisk mekanik är tvåkroppsproblemet att förutsäga rörelsen hos två massiva föremål som abstrakt ses som punktpartiklar . Problemet antar att de två objekten endast interagerar med varandra; den enda kraft som påverkar varje objekt kommer från det andra, och alla andra objekt ignoreras.

Det mest framträdande fallet av det klassiska tvåkroppsproblemet är gravitationsfallet (se även Kepler-problemet ), som uppstår inom astronomi för att förutsäga omlopp (eller flykt från omloppsbana) av objekt som satelliter , planeter och stjärnor . En tvåpunktspartikelmodell av ett sådant system beskriver nästan alltid dess beteende tillräckligt bra för att ge användbara insikter och förutsägelser.

En enklare modell för "en kropp", " centralkraftproblemet ", behandlar ett objekt som den orörliga källan till en kraft som verkar på det andra. Man försöker sedan förutsäga rörelsen hos det enda kvarvarande mobila objektet. En sådan approximation kan ge användbara resultat när ett objekt är mycket mer massivt än det andra (som med en lätt planet som kretsar kring en tung stjärna, där stjärnan kan behandlas som i huvudsak stationär).

Emellertid är enkroppsapproximationen vanligtvis onödig förutom som en språngbräda. För många krafter, inklusive gravitationskrafter, kan den allmänna versionen av tvåkroppsproblemet reduceras till ett par enkroppsproblem, vilket gör att det kan lösas fullständigt och ger en lösning som är tillräckligt enkel för att användas effektivt.

Däremot kan trekroppsproblemet (och, mer generellt, n -kroppsproblemet för n ≥ 3) inte lösas i termer av första integraler, förutom i speciella fall.

Resultat för framstående fall

Gravitation och andra omvända kvadratiska exempel

Tvåkroppsproblemet är intressant inom astronomi eftersom par av astronomiska objekt ofta rör sig snabbt i godtyckliga riktningar (så att deras rörelser blir intressanta), brett separerade från varandra (så att de inte kommer att kollidera) och ännu mer brett separerade från andra objekt ( så påverkan utifrån kommer att vara tillräckligt liten för att kunna ignoreras på ett säkert sätt).

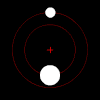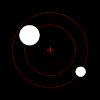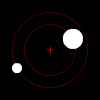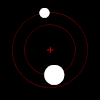
Under tyngdkraften kommer varje medlem av ett par sådana föremål att kretsa kring sin inbördes masscentrum i ett elliptiskt mönster, såvida de inte rör sig tillräckligt snabbt för att fly varandra helt, i vilket fall deras banor kommer att divergera längs andra plana koniska sektioner . Om ett föremål är mycket tyngre än det andra, kommer det att röra sig mycket mindre än det andra med hänvisning till den delade massan. Det inbördes masscentrumet kan till och med vara inuti det större föremålet.

För härledning av lösningarna på problemet, se Klassiskt centralkraftproblem eller Keplerproblem .

I princip gäller samma lösningar för makroskopiska problem som involverar objekt som interagerar inte bara genom gravitation, utan genom vilket annat attraktivt skalärt kraftfält som helst som lyder en omvänd kvadratisk lag , med elektrostatisk attraktion som det uppenbara fysiska exemplet. I praktiken uppstår sådana problem sällan. Förutom kanske i experimentella apparater eller annan specialiserad utrustning, möter vi sällan elektrostatiskt interagerande föremål som rör sig tillräckligt snabbt och i en sådan riktning att de undviker att kollidera, och/eller som är tillräckligt isolerade från sin omgivning.

Det dynamiska systemet i ett tvåkroppssystem under påverkan av vridmoment visar sig vara en Sturm-Liouville-ekvation .

Otillämpbarhet på atomer och subatomära partiklar

Även om tvåkroppsmodellen behandlar objekten som punktpartiklar, gäller klassisk mekanik endast för system av makroskopisk skala. De flesta beteenden hos subatomära partiklar kan inte förutsägas under de klassiska antagandena som ligger till grund för denna artikel eller genom att använda matematiken här.

Elektroner i en atom beskrivs ibland som "kretsar kring" dess kärna , efter en tidig gissning av Niels Bohr (detta är källan till termen " orbital "). Men elektroner kretsar faktiskt inte om kärnor i någon meningsfull mening, och kvantmekanik är nödvändig för någon användbar förståelse av elektronens verkliga beteende. Att lösa det klassiska tvåkroppsproblemet för en elektron som kretsar kring en atomkärna är missvisande och ger inte många användbara insikter.

Reduktion till två oberoende, enkroppsproblem

Det kompletta tvåkroppsproblemet kan lösas genom att omformulera det som två enkroppsproblem: ett trivialt och ett som innebär att lösa en partikels rörelse i en extern potential . Eftersom många enkroppsproblem kan lösas exakt, kan motsvarande tvåkroppsproblem också lösas.

Jacobi koordinerar för tvåkroppsproblem; Jacobi-koordinaterna är ${\boldsymbol {R}}={\frac {m_{1}}{M}}{\boldsymbol {x}}_{1 }+{\frac {m_{2}}{M}}{\boldsymbol {x}}_{2}$ och ${\boldsymbol {r}}={\boldsymbol { x}}_{1}-{\boldsymbol {x}}_{2}$ med $M=m_{1}+m_{2}\$ .

Låt x ₁ och x ₂ vara vektorpositionerna för de två kropparna, och m ₁ och m ₂ är deras massor. Målet är att bestämma banorna x ₁ ( t ) och x ₂ ( t ) för alla tider t , givet de initiala positionerna x ₁ ( t = 0) och x ₂ ( t = 0) och initialhastigheterna v ₁ ( t ) = 0) och 0) _. v2 ( t =

När den tillämpas på de två massorna, säger Newtons andra lag det

$$\mathbf {F} _{12}(\mathbf {x} _{1},\mathbf {x} _{2})=m_ {1}{\ddot {\mathbf {x} }}_{1}$$

 

 

 

 

(Ekvation)

$$\mathbf {F} _{21}(\mathbf {x} _{1},\mathbf {x} _{2})=m_ {2}{\ddot {\mathbf {x} }}_{2}$$

 

 

 

 

(Ekvation)

där F ₁₂ är kraften på massa 1 på grund av dess växelverkan med massa 2, och F ₂₁ är kraften på massa 2 på grund av dess växelverkan med massa 1. De två punkterna ovanpå x -positionsvektorerna betecknar deras andraderivata med avseende på till tid, eller deras accelerationsvektorer.

Att addera och subtrahera dessa två ekvationer frikopplar dem till två enkroppsproblem, som kan lösas oberoende av varandra. Att lägga till ekvationerna (1) och ( 2 ) resulterar i en ekvation som beskriver masscentrumets ( barycenter ) rörelse. Att subtrahera ekvation (2) från ekvation (1) resulterar däremot i en ekvation som beskriver hur vektorn r = x ₁ − x ₂ mellan massorna förändras med tiden. Lösningarna av dessa oberoende enkroppsproblem kan kombineras för att erhålla lösningarna för banorna x ₁ ( t ) och x ₂ ( t ) .

Rörelsecentrum (första enkroppsproblem)

Låt $\mathbf {R}$ vara positionen för systemets massacentrum ( barycenter ). Addering av kraftekvationerna (1) och (2) ger

$$m_{1}{\ddot {\mathbf {x} }}_{1} +m_{2}{\ddot {\mathbf {x} }}_{2}=(m_{1}+m_{2}){\ddot {\mathbf {R} }}=\mathbf {F} _ {12}+\mathbf {F} _{21}=0$$

där vi har använt Newtons tredje lag F ₁₂ = − F ₂₁ och var

$${\ddot {\mathbf {R} }}\equiv {\frac {m_{1}{\ddot {\mathbf {x} }}_{1}+m_{2}{\ddot {\mathbf {x} }}_{2}}{m_{1}+m_{2}}}.$$

Den resulterande ekvationen:

$${\ddot {\mathbf {R} }}=0$$

visar att hastigheten $\mathbf {v} ={\frac {dR}{dt}}$ för masscentrum är konstant, vilket följer att det totala rörelsemängden m ₁ v ₁ + m ₂ v ₂ är också konstant ( bevarande av momentum ). Följaktligen kan positionen R ( t ) för masscentrum alltid bestämmas från de initiala positionerna och hastigheterna.

Förskjutningsvektorrörelse (andra enkroppsproblem)

Att dividera båda kraftekvationerna med respektive massor, subtrahera den andra ekvationen från den första och arrangera om ger ekvationen

$${\ddot {\mathbf {r} }}={ \ddot {\mathbf {x} }}_{1}-{\ddot {\mathbf {x} }}_{2}=\left({\frac {\mathbf {F} _{12}}{m_ {1}}}-{\frac {\mathbf {F} _{21}}{m_{2}}}\right)=\left({\frac {1}{m_{1}}}+{\ frac {1}{m_{2}}}\right)\mathbf {F} _{12}$$

där vi återigen har använt Newtons tredje lag F ₁₂ = − F ₂₁ och där r är förskjutningsvektorn från massa 2 till massa 1, enligt definitionen ovan.

Kraften mellan de två objekten, som har sitt ursprung i de två objekten, bör endast vara en funktion av deras separation r och inte av deras absoluta positioner x ₁ och x ₂ ; annars skulle det inte finnas translationell symmetri , och fysikens lagar skulle behöva ändras från plats till plats. Den subtraherade ekvationen kan därför skrivas:

$$\mu {\ddot {\mathbf {r} }}=\mathbf {F} _{12}(\mathbf {x} _{1},\mathbf {x} _{2})=\mathbf {F} (\mathbf {r} )$$

där $\mu$ är den reducerade massan

$$\mu ={\frac {1}{{\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}}}={\frac {m_{1 }m_{2}}{m_{1}+m_{2}}}.$$

Att lösa ekvationen för r ( t ) är nyckeln till tvåkroppsproblemet. Lösningen beror på den specifika kraften mellan kropparna, som definieras av $\mathbf {F} (\mathbf {r} )$ . För fallet där $\mathbf {F} (\mathbf {r} )$ följer en omvänd kvadratisk lag , se Kepler-problemet .

När R ( t ) och r ( t ) väl har bestämts kan de ursprungliga banorna erhållas

$$\mathbf {x} _{1}(t)=\mathbf {R} (t)+{\frac {m_{2}}{m_{1}+m_{2}}}\mathbf {r} (t)$$

$$\mathbf {x} _{2}(t)=\mathbf {R} (t)-{\frac {m_{1}}{m_{1}+m_{2}}}\mathbf {r} (t)$$

vilket kan verifieras genom att ersätta definitionerna av R och r i de högra sidorna av dessa två ekvationer.

Tvåkroppsrörelsen är plan

Rörelsen av två kroppar i förhållande till varandra ligger alltid i ett plan (i masscentrumramen ) .

Bevis: Definierar systemets linjära rörelsemängd p och rörelsemängd L i systemet, med avseende på massans centrum, genom ekvationerna

$$\mathbf {L} =\mathbf {r} \times \mathbf {p} =\mathbf {r} \times \mu {\frac {d \mathbf {r} }{dt}},$$

där μ är den reducerade massan och r är den relativa positionen r ₂ − r ₁ (med dessa skrivna tar masscentrum som utgångspunkt, och alltså båda parallella med r ) är förändringshastigheten för rörelsemängden L lika med nettovridmomentet N

$$\mathbf {N} ={\frac {d\mathbf {L} }{dt}}={\dot {\ mathbf {r} }}\times \mu {\dot {\mathbf {r} }}+\mathbf {r} \times \mu {\ddot {\mathbf {r} }}\ ,$$

och använda egenskapen för vektorkorsprodukten att v × w = 0 för alla vektorer v och w som pekar i samma riktning,

$$\mathbf {N} \ =\ {\frac {d\mathbf {L} }{dt}}=\mathbf {r} \times \mathbf {F} \ ,$$

med   ^_ F = μd 2 r / dt ² .

Genom att introducera antagandet (sant för de flesta fysiska krafter, eftersom de följer Newtons starka tredje rörelselag ) att kraften mellan två partiklar verkar längs linjen mellan deras positioner, följer det att r × F = 0 och rörelsemängdsvektorn L är konstant ( konserverad). Därför är förskjutningsvektorn r och dess hastighet v alltid i planet vinkelrät mot den konstanta vektorn L .

Energi i tvåkroppssystemet

Om kraften F ( r ) är konservativ har systemet en potentiell energi U ( r ) , så den totala energin kan skrivas som

$$E_{\text{tot}}={\frac {1}{2}}m_{1}{\dot {\mathbf {x} }}_{1}^{2}+{\frac { 1}{2}}m_{2}{\dot {\mathbf {x} }}_{2}^{2}+U(\mathbf {r})={\frac {1}{2}}( m_{1}+m_{2}){\dot {\mathbf {R} }}^{2}+{1 \över 2}\mu {\dot {\mathbf {r} }}^{2}+ U(\mathbf {r} )$$

I masscentrumramen är den kinetiska energin lägst och den totala energin blir

$$E={\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}+U(\mathbf {r} )$$

Koordinaterna x ₁ och x ₂ kan uttryckas som

$$\mathbf {x} _{1}={\frac {\mu }{m_{1}}}\mathbf {r}$$

$$\mathbf {x} _{2}=-{\frac {\mu }{m_{2}}}\mathbf {r}$$

och på liknande sätt är energin E relaterad till energierna E ₁ och E ₂ som separat innehåller den kinetiska energin för varje kropp:

$${\begin{aligned}E_{1}&={\frac {\mu }{m_{1}}}E={\frac {1}{2}}m_{1 }{\dot {\mathbf {x} }}_{1}^{2}+{\frac {\mu }{m_{1}}}U(\mathbf {r} )\\[4pt]E_{ 2}&={\frac {\mu }{m_{2}}}E={\frac {1}{2}}m_{2}{\dot {\mathbf {x} }}_{2}^ {2}+{\frac {\mu }{m_{2}}}U(\mathbf {r} )\\[4pt]E_{\text{tot}}&=E_{1}+E_{2} \end{aligned}}$$

Centrala krafter

Huvudartikel: Klassiskt centralkraftproblem

För många fysiska problem är kraften F ( r ) en central kraft , dvs den är av formen

$$\mathbf {F} (\mathbf {r} )=F(r){\hat {\mathbf {r} }}$$

där r = | r | och r̂ = r / r är motsvarande enhetsvektor . Vi har nu:

$$\mu {\ddot {\mathbf {r} }}={F}(r){\hat {\mathbf {r} }}\ ,$$

där F ( r ) är negativ i fallet med en attraktionskraft.

Se även

• Energidrift
• Mittens ekvation
• Eulers trekroppsproblem
• Kepler omloppsbana
• Kepler problem
• n -kroppsproblem
• Virial teorem

Bibliografi

•   Landau LD ; Lifshitz EM (1976). Mekanik (3:e uppl.). New York: Pergamon Press . ISBN 0-08-029141-4 .
•   Goldstein H (1980). Klassisk mekanik (2:a uppl.). New York: Addison-Wesley . ISBN 0-201-02918-9 .

externa länkar

• Tvåkroppsproblem vid Eric Weissteins World of Physics