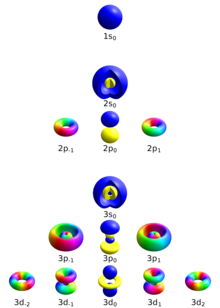Kvantnummer
| Del av en serie artiklar om |
| kvantmekanik |
|---|
Inom kvantfysik och kemi beskriver kvanttal värden på bevarade kvantiteter i ett kvantsystems dynamik . Kvanttal motsvarar egenvärden för operatorer som pendlar med Hamiltonian - kvantiteter som kan vara kända med precision samtidigt som systemets energi - och deras motsvarande egenrum. Tillsammans karaktäriserar en specifikation av alla kvanttal i ett kvantsystem fullt ut ett bastillstånd för systemet, och kan i princip mätas tillsammans .
En viktig aspekt av kvantmekaniken är kvantiseringen av många observerbara kvantiteter av intresse. I synnerhet leder detta till kvanttal som tar värden i diskreta uppsättningar av heltal eller halvheltal ; även om de kan närma sig oändligheten i vissa fall. Detta skiljer kvantmekaniken från klassisk mekanik där de värden som kännetecknar systemet såsom massa, laddning eller momentum, alla varierar kontinuerligt. Kvanttal beskriver ofta specifikt energinivåerna för elektroner i atomer, men andra möjligheter inkluderar rörelsemängd , spin , etc. En viktig familj är smakkvanttal – interna kvanttal som bestämmer typen av en partikel och dess interaktioner med andra partiklar genom grundläggande krafter . Vilket kvantsystem som helst kan ha ett eller flera kvanttal; det är alltså svårt att lista alla möjliga kvanttal.
Kvanttal som behövs för ett givet system
Antalet kvanttal varierar från system till system och har inget universellt svar. Därför måste dessa parametrar hittas för varje system som ska analyseras. Ett kvantiserat system kräver minst ett kvantnummer. Dynamiken (dvs. tidsutvecklingen) för varje kvantsystem beskrivs av en kvantoperator i form av en Hamiltonian , H . Det finns ett kvantnummer i systemet som motsvarar systemets energi; dvs ett av Hamiltonianens egenvärden . Det finns också ett kvantnummer för varje linjärt oberoende operator O som pendlar med Hamiltonian. En komplett uppsättning observerbara pendlingsvärden (CSCO) som pendlar med Hamiltonian kännetecknar systemet med alla dess kvanttal. Det finns ett ett-till-ett förhållande mellan kvanttalen och operatorerna för CSCO, där varje kvanttal tar ett av egenvärdena för dess motsvarande operator. Som ett resultat av den olika basen som godtyckligt kan väljas för att bilda en komplett uppsättning pendlingsoperatörer, kan olika uppsättningar av kvantnummer användas för beskrivningen av samma system i olika situationer.
Elektron i en atom
Fyra kvanttal kan helt beskriva en elektron i en atom:
- Huvudkvantnummer ( n )
- Azimutalt kvantnummer ( ℓ )
- Magnetiskt kvantnummer ( mℓ )
- Spin kvantnummer ( m s )
Interaktionen mellan spinn och orbital relaterar dock dessa siffror. En fullständig beskrivning av systemet kan alltså ges med färre kvanttal, om ortogonala val görs för dessa basvektorer.
Specificitet
Olika elektroner i ett system kommer att ha olika kvantantal. Till exempel den högst upptagna orbitala elektronen, den faktiska differentieringselektronen (dvs elektronen som skiljer ett element från den föregående), eller den differentierande elektronen enligt aufbau - approximationen . I lantan , som en ytterligare illustration, är de involverade elektronerna i 6:orna; 5d; och 4f orbitaler, respektive. I det här fallet är de huvudsakliga kvanttalen 6, 5 och 4.
Vanlig terminologi
Modellen som används här beskriver elektroner med fyra kvanttal, n , ℓ , m ℓ , m s , som anges nedan. Det är också den vanliga nomenklaturen i den klassiska beskrivningen av kärnpartikeltillstånd (t.ex. protoner och neutroner). En kvantbeskrivning av molekylära orbitaler kräver andra kvanttal, eftersom Hamiltonian och dess symmetri är olika.
Huvudkvantnummer
Det huvudsakliga kvanttalet beskriver elektronskalet, eller energinivån, för en elektron. Värdet på n sträcker sig från 1 till skalet som innehåller den yttersta elektronen i den atomen, dvs.
- n = 1, 2, ...
Till exempel, i cesium (Cs), finns den yttersta valenselektronen i skalet med energinivå 6, så en elektron i cesium kan ha ett n -värde från 1 till 6.
För partiklar i en tidsoberoende potential (se Schrödinger-ekvationen ) betecknar den också det n: te egenvärdet för Hamiltonian ( H ), det vill säga energin E , med bidraget på grund av rörelsemängd (termen som involverar J 2 ) utelämnad . Så detta nummer beror bara på avståndet mellan elektronen och kärnan (det vill säga den radiella koordinaten r ). Medelavståndet ökar med n . Därför sägs kvanttillstånd med olika huvudsakliga kvanttal tillhöra olika skal.
Azimutalt kvantnummer
Det azimutala kvantnumret, även känt som vinkelmomentet quantum number eller orbital quantum number , beskriver underskalet och ger storleken på den orbitala rörelsemängden genom relationen.
- L 2 = ħ 2 ℓ ( ℓ + 1)
Inom kemi och spektroskopi kallas ℓ = 0 s orbital, ℓ = 1 , p orbital, ℓ = 2 , d orbital och ℓ = 3 , f orbital.
Värdet på ℓ sträcker sig från 0 till n − 1 , så den första p-orbitalen ( ℓ = 1 ) visas i det andra elektronskalet ( n = 2 ), den första d-orbitalen ( ℓ = 2 ) visas i det tredje skalet ( n ) = 3 ), och så vidare:
- ℓ = 0, 1, 2,..., n − 1
Ett kvanttal som börjar på n = 3, ℓ = 0, beskriver en elektron i s-omloppsbanan för en atoms tredje elektronskal. Inom kemi är detta kvantnummer mycket viktigt, eftersom det anger formen på en atomomloppsbana och starkt påverkar kemiska bindningar och bindningsvinklar . Det azimutala kvantnumret kan också beteckna antalet vinkelnoder som finns i en orbital. Till exempel, för p-orbitaler, ℓ = 1 och därmed är mängden vinkelnoder i ap-orbitalen 1.
Orbitalformen ges också av azimutalt kvantnummer.
Magnetiskt kvantnummer
Det magnetiska kvantnumret beskriver den specifika omloppsbanan (eller "molnet") inom det underskalet, och ger projektionen av det omloppsmässiga vinkelmomentet längs en specificerad axel :
- Lz _ = mℓ ħ _
Värdena på m ℓ sträcker sig från − ℓ till ℓ , med heltalsintervall. [ sida behövs ]
s-underskalet ( ℓ = 0 ) innehåller bara en orbital, och därför kommer m ℓ för en elektron i en s-orbital alltid att vara 0. p-underskalet ( ℓ = 1 ) innehåller tre orbitaler (i vissa system, avbildade som tre " hantelformade" moln), så m ℓ för en elektron i ap-orbital kommer att vara −1, 0 eller 1. Underskalet d ( ℓ = 2 ) innehåller fem orbitaler, med m ℓ -värden på −2, −1, 0, 1 och 2.
Spin kvantnummer
Spinnkvantnumret beskriver elektronens inneboende rörelsemängdsrörelse inom varje orbital och ger projektionen av rörelsemängden S längs den specificerade axeln:
- S z = m s ħ .
I allmänhet sträcker sig värdena på m s från − s till s , där s är spinnkvanttalet , associerat med partikelns inneboende spinnvinkelmomentum:
- m s = − s , − s + 1, − s + 2, ..., s − 2, s − 1, s .
1/2 En , elektron har snurrtal s = 1/2 tillstånd . följaktligen kommer m s att vara ± , med hänvisning till "snurra upp" och "snurra ner" Varje elektron i varje enskild orbital måste ha olika kvanttal på grund av Pauli-uteslutningsprincipen , därför innehåller en orbital aldrig mer än två elektroner.
Regler
Det finns inga universella fasta värden för m ℓ och m s . Snarare m ℓ och m s -värdena godtyckliga . De enda begränsningarna för valen av dessa konstanter är att namnschemat som används inom en viss uppsättning beräkningar eller beskrivningar måste vara konsekvent (t.ex. kan orbitalen som upptas av den första elektronen i ap-orbitalen beskrivas som m ℓ = −1 eller m ℓ = 0 eller m ℓ = 1 , men m ℓ -värdet för nästa oparade elektron i den orbitalen måste vara annorlunda; ändå kan m ℓ som tilldelas elektroner i andra orbitaler igen vara m ℓ = −1 eller m ℓ = 0 eller m ^ = 1 ).
Dessa regler sammanfattas enligt följande:
namn Symbol Menande Värdeintervall Värdeexempel Huvudkvantnummer n skal 1 ≤ n n = 1, 2, 3, … Azimutalt kvanttal ( vinkelmomentum ) ℓ subshell (s orbital är listad som 0, p orbital som 1 etc.) 0 ≤ ℓ ≤ n − 1
för n = 3 : ℓ = 0, 1, 2 (s, p, d)Magnetiskt kvanttal (projektion av rörelsemängd ) m ℓ Orbital (orientering av orbital) − ℓ ≤ m ℓ ≤ ℓ
för ℓ = 2 : m ℓ = −2, −1, 0, 1, 2Spin kvantnummer m s elektronens spinn (− 1 / 2 = "snurra ner", 1 / 2 = "snurra upp") − s ≤ m s ≤ s
m s 1/2 för _ 1/2 en = − + elektron s = 1/2 , _ , så
Exempel : Kvanttalen som används för att referera till de yttersta valenselektronerna i en kolatom (C) , som finns i 2p atomomloppsbanan , är; n = 2 (2: m s = 1/2 . a elektronskalet), ℓ = 1 (p orbitalt underskal ), m ℓ = 1, 0, −1 , (parallella spinn)
Resultat från spektroskopi visade att upp till två elektroner kan ockupera en enda orbital. Två elektroner kan dock aldrig ha samma exakta kvanttillstånd eller samma uppsättning kvanttal enligt Hunds regler , som tar upp Pauli-uteslutningsprincipen . Ett fjärde kvanttal, som representerade spinn med två möjliga värden, lades till som ett ad hoc- antagande för att lösa konflikten; detta antagande skulle senare förklaras i detalj av relativistisk kvantmekanik och från resultaten av det berömda Stern-Gerlach-experimentet .
Bakgrund
Många olika modeller har föreslagits genom kvantmekanikens historia , men det mest framträdande nomenklatursystemet skapades från Hund-Mullikens molekylära orbitalteori av Friedrich Hund , Robert S. Mulliken och bidrag från Schrödinger , Slater och John Lennard-Jones . Detta nomenklatursystem inkorporerade Bohrs energinivåer, Hund-Mullikens orbitalteori och observationer av elektronspin baserat på spektroskopi och Hunds regler .
Totalt antal vinkelmoment
Total rörelsemängd för en partikel
När man tar hänsyn till spin-omloppsinteraktionen pendlar inte L- och S -operatorerna längre med Hamiltonian , och deras egenvärden förändras därför över tiden. Därför bör en annan uppsättning kvanttal användas. Detta set innehåller
-
Det totala rörelsemängdskvantumtalet :
- j = | ℓ ± s |
vilket ger den totala rörelsemängden genom relationen
- J 2 = ħ 2 j ( j + 1)
-
Projektionen av den totala rörelsemängden längs en specificerad axel :
- m j = − j , − j + 1, − j + 2, ..., j − 2, j − 1, j
analogt med ovanstående och uppfyller
- m j = m ℓ + m s och | mℓ _ + m s | ≤ j
-
Paritet
Detta är egenvärdet under reflektion: positivt (+1) för tillstånd som kom från jämn ℓ och negativt (−1) för tillstånd som kom från udda ℓ . Den förra är också känd som jämn paritet och den senare som udda paritet , och ges av
- P = (−1) ℓ
Tänk till exempel på följande 8 tillstånd, definierade av deras kvanttal:
n ℓ m ℓ m s ℓ + s ℓ − s m ℓ + m s (1) 2 1 1 + 1/2 _ _ 3/2 _ _ 1/2 _ _3/2 _ _ (2) 2 1 1 − 1/2 _ _ 3/2 _ _ 1/2 _ _ 1/2 _ _ (3) 2 1 0 + 1/2 _ _ 3/2 _ _ 1/2 _ _ 1/2 _ _ (4) 2 1 0 − 1/2 _ _ 3/2 _ _ 1/2 _ _ − 1/2 _ _ (5) 2 1 −1 + 1/2 _ _ 3/2 _ _ 1/2 _ _ − 1/2 _ _ (6) 2 1 −1 − 1/2 _ _ 3/2 _ _ 1/2 _ _− 3/2 _ _ (7) 2 0 0 + 1/2 _ _ 1/2 _ _ − 1/2 _ _ 1/2 _ _ (8) 2 0 0 − 1/2 _ _ 1/2 _ _ − 1/2 _ _ − 1/2 _ _
Kvanttillstånden i systemet kan beskrivas som en linjär kombination av dessa 8 tillstånd . Men i närvaro av spin-omloppsinteraktion , om man vill beskriva samma system med 8 tillstånd som är egenvektorer till Hamiltonian (dvs var och en representerar ett tillstånd som inte blandas med andra över tiden), bör vi överväga följande 8 stater:
j m j paritet 3/2 _ _ 3/2 _ _ udda kommer från stat (1) ovan 3/2 _ _ 1/2 _ _ udda kommer från staterna (2) och (3) ovan 3/2 _ _ − 1/2 _ _ udda kommer från staterna (4) och (5) ovan 3/2 _ _ − 3/2 _ _ udda kommer från stat (6) ovan 1/2 _ _ 1/2 _ _ udda kommer från staterna (2) och (3) ovan 1/2 _ _ − 1/2 _ _ udda kommer från staterna (4) och (5) ovan 1/2 _ _ 1/2 _ _ även kommer från stat (7) ovan 1/2 _ _ − 1/2 _ _ även kommer från stat (8) ovan
Nukleära rörelsemängdskvantumtal
I kärnor har hela sammansättningen av protoner och neutroner ( nukleoner ) ett resulterande rörelsemängd på grund av vinkelmomentet för varje nukleon, vanligtvis betecknat I . Om den totala rörelsemängden för en neutron är j n = ℓ + s 1/2 och för en proton är j p = ℓ + s (där s för protoner och neutroner råkar vara igen ( se not )), då är kärnvinkeln momentum kvanttal I ges av:
- Jag = | j n − j p |, | j n − j p | + 1, | j n − j p | + 2, ..., ( j n + j p ) − 2, ( j n + j p ) − 1, ( j n + j p )
Notera: Det orbitala vinkelmomentet för kärntillstånden (och atomära) tillstånd är alla heltalsmultiplar av ħ medan neutronens och protonens inneboende vinkelmoment är halvheltalsmultiplar. Det bör vara omedelbart uppenbart att kombinationen av nukleonernas inneboende spinn med deras orbitala rörelse alltid kommer att ge halvheltalsvärden för det totala spinnet, I , för alla udda A-kärnor och heltalsvärden för alla jämna A-kärnor.
Paritet med talet I används för att märka nukleära rörelsemängdstillstånd, exempel på vissa isotoper av väte (H), kol (C) och natrium (Na) är;
1 1 HI = ( _ 1/2 ) +
9 6 CI = ( _ 3/2 ) −
20 11 NaI = 2+
2 1 HI = 1+
10 6 CI = 0 +
21 11 NaI = ( _ 3/2 ) +
3 1 HI = ( _ 1/2 ) +
11 6 CI = ( _ 3/2 ) −
22 11 NaI = 3+
12 6 CI = 0 +
23 11 NaI = ( _ 3/2 ) +
13 6 CI = ( _ 1/2 ) −
24 11 NaI = 4+
14 6 CI = 0 +
25 11 NaI = ( _ 5/2 ) +
15 6 CI = ( _ 1/2 ) +
26 11 NaI = 3+
Orsaken till de ovanliga fluktuationerna i I , även om skillnader på bara en nukleon beror på det udda och jämna antalet protoner och neutroner – par av nukleoner har en total rörelsemängd på noll (precis som elektroner i orbitaler), vilket lämnar en udda eller jämna antal oparade nukleoner. Egenskapen hos kärnspinn är en viktig faktor för driften av NMR- spektroskopi inom organisk kemi , och MRI inom nuklearmedicin , på grund av det kärnmagnetiska momentet som interagerar med ett externt magnetfält .
Elementarpartiklar
Elementarpartiklar innehåller många kvanttal som vanligtvis sägs vara inneboende för dem. Det bör dock förstås att elementarpartiklarna är kvanttillstånd av standardmodellen för partikelfysik, och därför har kvanttalen för dessa partiklar samma relation till Hamiltonian för denna modell som kvanttalen för Bohr-atomen gör till dess Hamiltonian . Med andra ord, varje kvantnummer betecknar en symmetri av problemet. Det är mer användbart i kvantfältteori att skilja mellan rumtid och interna symmetrier.
Typiska kvanttal relaterade till rymdtidssymmetrier är spin (relaterat till rotationssymmetri), pariteten , C-paritet och T-paritet (relaterad till Poincarés symmetri av rymdtid ). Typiska interna symmetrier [ förtydligande behövs ] är leptonnummer och baryonnummer eller den elektriska laddningen . (För en fullständig lista över kvantnummer av detta slag, se artikeln om smak .)
Multiplikativa kvanttal
De flesta bevarade kvanttal är additiva, så i en elementarpartikelreaktion bör summan av kvanttalen vara densamma före och efter reaktionen. Vissa, vanligtvis kallade en paritet , är dock multiplikativa; dvs deras produkt är konserverad. Alla multiplikativa kvanttal tillhör en symmetri (som paritet) där att tillämpa symmetritransformationen två gånger är likvärdigt med att göra ingenting ( involution ).
Se även
Anteckningar
Vidare läsning
- Dirac, Paul AM (1982). Kvantmekanikens principer . Oxford University Press. ISBN 0-19-852011-5 .
- Griffiths, David J. (2004). Introduktion till kvantmekanik (2nd ed.) . Prentice Hall. ISBN 0-13-805326-X .
- Halzen, Francis & Martin, Alan D. (1984). QUARKS AND LEPTONS: En introduktionskurs i modern partikelfysik . John Wiley & Sons. ISBN 0-471-88741-2 .
- Eisberg, Robert Martin; Resnick, Robert (1985). Kvantfysik av atomer, molekyler, fasta ämnen, kärnor och partiklar ( 2:a upplagan). John Wiley & Sons. ISBN 978-0-471-87373-0 – via Internet Archive .