Uppskattningsstatistik

Uppskattningsstatistik , eller helt enkelt uppskattning , är ett ramverk för dataanalys som använder en kombination av effektstorlekar , konfidensintervall , precisionsplanering och metaanalys för att planera experiment, analysera data och tolka resultat. Den kompletterar hypotestestningsmetoder som nollhypotes signifikanstestning (NHST), genom att gå bortom frågan om en effekt finns eller inte, och ger information om hur stor en effekt är. Uppskattningsstatistik kallas ibland för den nya statistiken .

Det primära syftet med uppskattningsmetoder är att rapportera en effektstorlek (en punktskattning ) tillsammans med dess konfidensintervall , varav det senare är relaterat till uppskattningens precision. Konfidensintervallet sammanfattar en rad sannolika värden för den underliggande populationseffekten. Förespråkare av uppskattning ser rapportering av ett P -värde som en ohjälpsam distraktion från den viktiga verksamheten att rapportera en effektstorlek med dess konfidensintervall, och anser att uppskattning bör ersätta signifikanstestning för dataanalys.

Historia

Från och med 1929 publicerade fysikern Raymond Thayer Birge granskningsartiklar där han använde vägda medelvärdensmetoder för att beräkna uppskattningar av fysiska konstanter, en procedur som kan ses som föregångaren till modern metaanalys .

På 1960-talet antogs skattningsstatistik av icke-fysikaliska vetenskaper med utvecklingen av den standardiserade effektstorleken av Jacob Cohen .

På 1970-talet var den moderna forskningssyntesen pionjär av Gene V. Glass med den första systematiska översikten och metaanalysen för psykoterapi. Detta banbrytande arbete påverkade sedan antagandet av metaanalyser för medicinska behandlingar mer generellt.

På 1980- och 1990-talen utökades och förfinades uppskattningsmetoderna av biostatistiker inklusive Larry Hedges , Michael Borenstein, Doug Altman , Martin Gardner och många andra, med utvecklingen av den moderna (medicinska) metaanalysen .

Från och med 1980-talet blev den systematiska översikten , som användes i samband med metaanalys, en teknik som används mycket inom medicinsk forskning. Det finns över 200 000 hänvisningar till "metaanalys" i PubMed .

På 1990-talet förbjöd redaktör Kenneth Rothman användningen av p-värden från tidskriften Epidemiology ; efterlevnaden var hög bland författarna men detta förändrade inte väsentligt deras analytiska tänkande.

På 2010-talet publicerade Geoff Cumming en lärobok dedikerad till skattningsstatistik, tillsammans med programvara i Excel utformad för att lära ut effektstorlekstänkande, främst till psykologer. Också på 2010-talet användes uppskattningsmetoder alltmer inom neurovetenskapen.

År 2013 rekommenderade American Psychological Associations publikationsmanual att använda uppskattning utöver hypotestestning. Även 2013 gav dokumentet Uniform Requirements for Manuscripts Submitted to Biomedical Journals en liknande rekommendation: "Undvik att enbart förlita sig på statistisk hypotestestning, såsom P-värden, som misslyckas med att förmedla viktig information om effektstorlek."

Under 2019 skrev över 800 forskare under en öppen kommentar som uppmanade till att överge hela konceptet med statistisk signifikans.

År 2019 införde Society for Neuroscience -tidskriften eNeuro en policy som rekommenderar användning av uppskattningsgrafik som den föredragna metoden för datapresentation. Och 2022 rekommenderade International Society of Physiotherapy Journal Editors användningen av uppskattningsmetoder istället för statistiska nollhypotestest.

Trots det utbredda antagandet av metaanalys för klinisk forskning och rekommendationer från flera stora förlagsinstitutioner, används inte uppskattningsramverket rutinmässigt i primär biomedicinsk forskning.

Metodik

Många signifikanstest har en uppskattningsmotsvarighet; i nästan alla fall kan testresultatet (eller dess p-värde ) enkelt ersättas med effektstorleken och en precisionsuppskattning. Till exempel, istället för att använda Students t-test , kan analytikern jämföra två oberoende grupper genom att beräkna medelskillnaden och dess 95 % konfidensintervall . Motsvarande metoder kan användas för ett parat t-test och flera jämförelser. På liknande sätt, för en regressionsanalys, skulle en analytiker rapportera bestämningskoefficienten (R ² ) och modellekvationen istället för modellens p-värde.

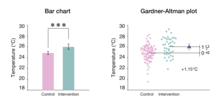
Förespråkare för skattningsstatistik varnar dock för att bara rapportera ett fåtal siffror. Det rekommenderas snarare att analysera och presentera data med hjälp av datavisualisering. Exempel på lämpliga visualiseringar inkluderar Scatter-plot för regression och Gardner-Altman-plot för två oberoende grupper. Medan historiska datagruppplottar (stapeldiagram, boxplott och fiolplottor) inte visar jämförelsen, lägger uppskattningsplott till en andra axel för att explicit visualisera effektstorleken.

Gardner–Altman-intrigen. Vänster: Ett vanligt stapeldiagram som använder asterisker för att visa att skillnaden är "statistiskt signifikant". Till höger: En Gardner–Altman-plot som visar alla datapunkter, tillsammans med medelskillnaden och dess konfidensintervall.

Gardner–Altmans handling

Gardner–Altman medelskillnadsdiagrammet beskrevs först av Martin Gardner och Doug Altman 1986; det är en statistisk graf utformad för att visa data från två oberoende grupper. Det finns också en version som är lämplig för parad data . De viktigaste instruktionerna för att göra detta diagram är följande: (1) visa alla observerade värden för båda grupperna sida vid sida; (2) placera en andra axel till höger, förskjuten för att visa medelskillnadsskalan; och (3) plotta medelskillnaden med dess konfidensintervall som en markör med felstaplar. Gardner-Altman-plottar kan genereras med DABEST-Python eller dabestr ; alternativt kan analytikern använda GUI-programvara som appen Estimation Stats .

Cumming-intrigen. En Cumming-plot som återges av webbapplikationen EstimationStats . I den övre panelen visas alla observerade värden. Effektstorlekarna, samplingsfördelningen och 95 % konfidensintervall plottas på en separat axel under rådata. För varje grupp ritas sammanfattande mätningar (medelvärde ± standardavvikelse) som mellanrumslinjer.

Cumming tomt

För flera grupper introducerade Geoff Cumming användningen av en sekundär panel för att plotta två eller flera medelskillnader och deras konfidensintervall, placerade under panelen för observerade värden; detta arrangemang möjliggör enkel jämförelse av medelskillnader ('deltas') över flera datagrupperingar. Cumming-diagram kan genereras med ESCI-paketet , DABEST eller appen Estimation Stats .

Andra metoder

Utöver medelskillnaden finns det många andra effektstorlekstyper , alla med relativa fördelar. Huvudtyper inkluderar effektstorlekar i Cohen's d -klassen av standardiserade mått och bestämningskoefficienten (R ² ) för regressionsanalys . För icke-normala fördelningar finns det ett antal mer robusta effektstorlekar, inklusive Cliffs delta och Kolmogorov-Smirnov-statistiken .

Brister i hypotesprövning

Vid hypotestestning är det primära syftet med statistiska beräkningar att erhålla ett p-värde , sannolikheten att se ett erhållet resultat, eller ett mer extremt resultat, när man antar att nollhypotesen är sann. Om p-värdet är lågt (vanligtvis < 0,05) uppmuntras den statistiska läkaren att förkasta nollhypotesen. Förespråkare för uppskattning avvisar giltigheten av hypotestestning av bland annat följande skäl:

P-värden misstolkas lätt och ofta. Till exempel är p-värdet ofta felaktigt tänkt som "sannolikheten att nollhypotesen är sann."
Nollhypotesen är alltid fel för varje uppsättning observationer: det finns alltid någon effekt, även om den är minimal.
Hypotestestning ger dikotoma ja-nej-svar, samtidigt som viktig information om magnitud förkastas.
Varje särskilt p-värde uppstår genom interaktionen av effektstorleken , urvalsstorleken (allt annat lika ger en större urvalsstorlek ett mindre p-värde) och samplingsfel .
Vid låg effekt avslöjar simulering att samplingsfel gör p-värden extremt flyktiga.

Fördelar med uppskattningsstatistik

Fördelar med konfidensintervall

Konfidensintervall beter sig på ett förutsägbart sätt. Per definition har 95 % konfidensintervall en 95 % chans att täcka det underliggande populationsmedelvärdet (μ). Denna funktion förblir konstant med ökande urvalsstorlek; det som förändras är att intervallet blir mindre. Dessutom är 95 % konfidensintervall också 83 % prediktionsintervall: ett (för experimentellt) konfidensintervall har 83 % chans att täcka ett framtida experiments medelvärde. Att känna till ett enskilt experiments 95 % konfidensintervall ger därför analytikern ett rimligt intervall för populationsmedelvärdet. Icke desto mindre ger konfidensfördelningar och posteriorfördelningar mycket mer information än en enstaka punktuppskattning eller intervall, vilket kan förvärra dikotomt tänkande enligt intervallet som täcker eller inte täcker ett "noll" värde av intresse (dvs. Neymans induktiva beteende i motsats till till Fishers).

Evidensbaserad statistik

Psykologiska studier av uppfattningen av statistik visar att rapportering av intervalluppskattningar lämnar en mer korrekt uppfattning om data än rapportering av p-värden.

Precisionsplanering

Precisionen för en uppskattning definieras formellt som 1/ varians , och liksom makt, ökar (förbättras) med ökande urvalsstorlek. Precis som kraft är en hög precisionsnivå dyr; Ansökningar om forskningsbidrag skulle helst omfatta precisions-/kostnadsanalyser. Förespråkare för uppskattning tror att precisionsplanering bör ersätta makt eftersom statistisk makt i sig är begreppsmässigt kopplad till signifikanstestning. Precisionsplanering kan göras med webbappen ESCI .

Se även