Steinitz sats

Inom polyedrisk kombinatorik , en gren av matematiken, är Steinitz sats en karakterisering av de oriktade graferna som bildas av kanterna och hörnen av tredimensionella konvexa polyedrar : de är exakt de 3-vertex-anslutna plana graferna . Det vill säga, varje konvex polyeder bildar en 3-kopplad plan graf, och varje 3-kopplad plan graf kan representeras som grafen för en konvex polyeder. Av denna anledning är de 3-kopplade plana graferna också kända som polyedriska grafer .

Detta resultat ger en klassificeringssats för de tredimensionella konvexa polyedrarna, något som inte är känt i högre dimensioner. Den ger en fullständig och rent kombinatorisk beskrivning av graferna för dessa polyedrar, vilket gör att andra resultat på dem, såsom Eberhards sats om realiseringen av polyedrar med givna typer av ansikten, lättare kan bevisas, utan hänvisning till dessa formers geometri. . Dessutom har det använts i grafritning , som ett sätt att konstruera tredimensionella visualiseringar av abstrakta grafer. Branko Grünbaum har kallat detta teorem "det viktigaste och djupaste kända resultatet på 3-polytoper ."

Teoremet förekommer i en publikation från 1922 av Ernst Steinitz , efter vilken den är uppkallad. Det kan bevisas genom matematisk induktion (som Steinitz gjorde), genom att hitta minimienergitillståndet för ett tvådimensionellt fjädersystem och lyfta resultatet till tre dimensioner, eller genom att använda cirkelpackningssatsen . Flera förlängningar av satsen är kända, där polyedern som realiserar en given graf har ytterligare begränsningar; till exempel är varje polyedergraf grafen för en konvex polyeder med heltalskoordinater, eller grafen för en konvex polyeder vars alla kanter tangerar en gemensam mellansfär .

Definitioner och uttalande av satsen

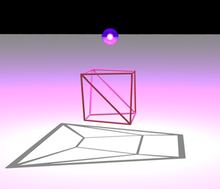
Att belysa skelettet av en konvex polyeder från en ljuskälla nära ett av dess ansikten får dess skuggor att bilda ett plant Schlegel-diagram .

En oriktad graf är ett system av hörn och kanter , där varje kant förbinder två av hörnen. Som är vanligt inom grafteorin, för Steinitzs sats är dessa grafer begränsade till att vara ändliga (hörn och kanter är ändliga mängder ) och enkla (inga två kanter förbinder samma två hörn, och ingen kant förbinder en vertex till sig själv) . Från vilken polyeder som helst kan man bilda en graf, genom att låta grafens hörn motsvara polyhedronens hörn och genom att koppla ihop två grafiska hörn med en kant närhelst de motsvarande två polyedertopparna är ändpunkterna på en kant på polyederen. Denna graf är känd som skelettet av polyhedron.

En graf är plan om den kan ritas med sina hörn som punkter i det euklidiska planet och dess kanter som kurvor som förbinder dessa punkter, så att inga två kantkurvor korsar varandra och så att punkten som representerar en vertex ligger på kurvan representerar en kant endast när spetsen är en ändpunkt på kanten. Genom Fárys sats kan varje plan ritning rätas ut så att kurvorna som representerar kanterna är linjesegment . En graf är 3-kopplad om den har mer än tre hörn och, efter att två av dess hörn har tagits bort, förblir alla andra hörn anslutna med en väg. Steinitz sats säger att dessa två villkor är både nödvändiga och tillräckliga för att karakterisera skelett av tredimensionella konvexa polyedrar: en given graf $G$ är grafen för en konvex tredimensionell polyeder, om och endast om ${\ displaystyle G}$ är plan och 3-vertex-ansluten.

Bevis

Illustration av beviset för Balinskis teorem , som visar nolluppsättningen av en linjär funktion (blå) som passerar genom två givna hörn (gul) och banorna i simplexmetoden som förbinder den återstående grafen (grön)

En riktning av Steinitz sats (den lättare riktningen att bevisa) säger att grafen för varje konvex polyeder är plan och 3-kopplad. Som visas i illustrationen kan planaritet visas genom att använda ett Schlegel-diagram : om man placerar en ljuskälla nära ena sidan av polyedern och ett plan på den andra sidan, kommer skuggorna på polyederkanterna att bilda en plan graf, inbäddad på ett sådant sätt att kanterna är raka linjesegment. 3-anslutningen för en polyedrisk graf är ett specialfall av Balinskis sats att grafen för någon $k$ -dimensionell konvex polytop är $k$ -ansluten. Anslutningen av grafen för en polytop, efter att ha tagit bort någon $k-1$ av dess hörn, kan bevisas genom att välja ytterligare en vertex ${\displaystyle v} ,$ hitta en linjär funktion som är noll på resulterande uppsättning $k$ hörn, och följa banorna som genereras av simplexmetoden för att koppla varje vertex till en av två extrema hörn av den linjära funktionen, med den valda vertexen $v$ kopplad till båda.

Den andra, svårare, riktningen i Steinitz sats säger att varje plan 3-kopplad graf är grafen för en konvex polyeder. Det finns tre standardmetoder för denna del: bevis genom induktion, lyftning av tvådimensionella Tutte-inbäddningar till tre dimensioner med Maxwell-Cremona-överensstämmelsen, och metoder som använder cirkelpackningssatsen för att generera en kanonisk polyeder .

Induktion

Δ-Y och Y-Δ transformeringar av en polyeder

Även om Steinitz ursprungliga bevis inte uttrycktes i termer av grafteori, kan det skrivas om i dessa termer, och innebär att hitta en sekvens av Δ-Y och Y-Δ-transformationer som reducerar vilken 3-kopplad plan graf som helst till $K_ {4}$ , grafen för tetraedern. En Y-Δ-transform tar bort en grad-tre vertex från en graf och lägger till kanter mellan alla dess tidigare grannar om dessa kanter inte redan fanns; den omvända transformationen, en Δ-Y-transform, tar bort kanterna på en triangel från en graf och ersätter dem med en ny grad-tre vertex intill samma tre hörn. När en sådan sekvens väl hittats kan den vändas om och omvandlas till geometriska operationer som bygger upp den önskade polyedern steg för steg med utgångspunkt från en tetraeder. Varje Y-A-transform i den omvända sekvensen kan utföras geometriskt genom att skära av en vertex på tre grader från en polyeder. En Δ-Y-transform i den omvända sekvensen kan utföras geometriskt genom att ta bort en triangulär yta från en polyeder och förlänga dess angränsande ytor tills den punkt där de möts, men bara när den trippel skärningspunkten för de tre angränsande ytorna är på bortre sidan av det borttagna ansiktet från polyedern. När den trippel skärningspunkten inte är på bortre sidan av denna yta, räcker det med en projektiv transformation av polyedern för att flytta den till rätt sida. Därför, genom induktion av antalet Δ-Y och Y-Δ transformationer som behövs för att reducera en given graf till $K_{4}$ , kan varje polyedrisk graf realiseras som en polyeder.

Ett senare arbete av Epifanov stärkte Steinitz bevis på att varje polyedrisk graf kan reduceras till $K_{4}$ genom Δ-Y och Y-Δ transformationer. Epifanov bevisade att om två hörn specificeras i en plan graf, så kan grafen reduceras till en enda kant mellan dessa terminaler genom att kombinera Δ-Y och Y-Δ transformationer med serie-parallella reduktioner . Epifanovs bevis var komplicerat och icke-konstruktivt, men det förenklades av Truemper med metoder baserade på grafiska mindretal . Truemper observerade att varje rutnätsgraf är reducerbar med Δ-Y och Y-Δ-transformationer på detta sätt, att denna reducerbarhet bevaras av grafiska minorer, och att varje plan graf är en minor av en rutnätsgraf. Denna idé kan användas för att ersätta Steinitz lemma om att det finns en reduktionssekvens. Efter detta utbyte kan resten av beviset utföras med induktion på samma sätt som Steinitz originalbevis. För dessa bevis, utförda med användning av något av sätten att hitta sekvenser av Δ-Y- och Y-Δ-transformeringar, finns det polyedriska grafer som kräver ett icke-linjärt antal steg. Mer exakt kan varje plan graf reduceras med ett antal steg som högst proportionellt mot $n^{3/2}$ , och oändligt många grafer kräver ett antal steg åtminstone proportionellt mot $n^{3/2}$ , där $n$ är antalet hörn i grafen.

En alternativ form av induktionssäkring är baserad på att ta bort kanter (och komprimera ut de två graders hörn som kan finnas kvar efter detta avlägsnande) eller att dra ihop kanterna och bilda en mindre av den givna plana grafen. Vilken polyedrisk graf som helst kan reduceras till $K_{4}$ med ett linjärt antal av dessa operationer, och återigen kan operationerna vändas och de omvända operationerna utföras geometriskt, vilket ger en polyedrisk realisering av grafen. Men även om det är enklare att bevisa att det finns en reduktionssekvens för denna typ av argument, och reduktionssekvenserna är kortare, är de geometriska stegen som behövs för att vända sekvensen mer komplicerade.

Lyft

Jämviktsspänning på grafen för en kub

En frustration som lyfter den stressade ritningen (med samma 2d-positioner) till 3d

Om en graf ritas i planet med räta linjekanter, definieras en jämviktsspänning som en tilldelning av reella tal (vikter) som inte är noll till kanterna, med egenskapen att varje vertex är i den position som ges av det viktade medelvärdet av dess grannar. Enligt Maxwell-Cremona-överensstämmelsen kan en jämviktsspänning lyftas till en bitvis linjär kontinuerlig tredimensionell yta så att kanterna som bildar gränserna mellan de plana delarna av ytan skjuter ut mot den givna ritningen. Vikten och längden av varje kant bestämmer skillnaden i lutningar av ytan på vardera sidan av kanten, och villkoret att varje vertex är i jämvikt med sina grannar är ekvivalent med villkoret att dessa lutningsskillnader får ytan att möta sig korrekt i närheten av vertexet. Positiva vikter översätts till konvexa dihedriska vinklar mellan två ytor av den bitvis linjära ytan, och negativa vikter översätts till konkava dihedriska vinklar. Omvänt kommer varje kontinuerlig styckvis linjär yta från en jämviktsspänning på detta sätt. Om en ändlig plan graf ritas och ges en jämviktsspänning på ett sådant sätt att alla inre kanter på ritningen har positiva vikter, och alla yttre kanter har negativa vikter, då genom att översätta denna spänning till en tredimensionell yta på detta sätt, och genom att sedan ersätta den plana ytan som representerar grafens utsida med dess komplement i samma plan, erhåller man en konvex polyeder, med den ytterligare egenskapen att dess vinkelräta projektion på planet inte har några korsningar.

Maxwell-Cremona-korrespondensen har använts för att erhålla polyedriska realiseringar av polyedriska grafer genom att kombinera den med en planritningsmetod av WT Tutte, Tutte- inbäddningen . Tuttes metod börjar med att fixera en sida av en polyedrisk graf i konvex position i planet. Denna yta kommer att bli den yttre ytan av en ritning av en graf. Metoden fortsätter genom att sätta upp ett system av linjära ekvationer i vertexkoordinaterna, enligt vilket varje återstående vertex ska placeras vid medelvärdet av sina grannar. Sedan, som Tutte visade, kommer detta ekvationssystem att ha en unik lösning där varje sida av grafen är ritad som en konvex polygon. Intuitivt beskriver den här lösningen mönstret som skulle erhållas genom att ersätta de inre kanterna på grafen med idealiska fjädrar och låta dem sätta sig till sitt minimala energitillstånd. Resultatet är nästan en jämviktsspänning: om man tilldelar vikt en till varje inre kant, är varje inre spets på ritningen i jämvikt. Det är dock inte alltid möjligt att tilldela de yttre kanterna negativa tal så att de också är i jämvikt. En sådan tilldelning är alltid möjlig när den yttre ytan är en triangel, och därför kan denna metod användas för att realisera vilken polyedrisk graf som helst som har en triangulär yta. Om en polyedrisk graf inte innehåller en triangulär yta, innehåller dess dubbla graf en triangel och är också polyedrisk, så man kan realisera dualen på detta sätt och sedan realisera den ursprungliga grafen som den polära polyedern för den dubbla realiseringen. En alternativ metod för att realisera polyedrar med hjälp av lyftningar undviker dualitet genom att välja vilken yta som helst med högst fem hörn som den yttre ytan. Varje polyedrisk graf har en sådan yta, och genom att välja den fasta formen på denna yta mer noggrant, kan Tutte-inbäddningen av resten av grafen lyftas.

Cirkelpackning

En polyeder realiserad från en cirkelpackning på den blå mellansfären. Varje polyedertopp representeras i packningen av sin horisontcirkel (röd). Varje ansikte representeras av cirkeln som görs av dess skärning med sfären.

Enligt en variant av cirkelpackningssatsen finns det för varje polyedrisk graf ett system av cirklar i planet eller på vilken sfär som helst, som representerar grafens hörn och ytor, så att:

varje två angränsande hörn av grafen representeras av tangentcirklar ,
var och en av två intilliggande ytor av grafen representeras av tangentcirkel,
varje par av en vertex och en yta som den berör representeras av cirklar som korsar i rät vinkel , och
alla andra par av cirklar är separerade från varandra.

Samma system av cirklar bildar en representation av den dubbla grafen genom att byta rollerna för cirklar som representerar hörn och cirklar som representerar ansikten. Från vilken som helst sådan representation på en sfär, inbäddad i det tredimensionella euklidiska rummet, kan man bilda en konvex polyeder som är kombinatoriskt ekvivalent med den givna grafen, som en skärning av halvrum vars gränser går genom ansiktscirklarna . Från varje hörn av denna polyeder är horisonten på sfären, sett från den hörn, cirkeln som representerar den. Denna horisontegenskap bestämmer den tredimensionella positionen för varje vertex, och polyedern kan på motsvarande sätt definieras som det konvexa skrovet på hörnen, placerat på detta sätt. Sfären blir mittsfär : varje kant av polyedern tangerar sfären, vid en punkt där två tangerande vertexcirklar korsar två tangentytacirklar.

Realisationer med tilläggsfastigheter

Heltalskoordinater

Det är möjligt att bevisa en starkare form av Steinitzs sats, att vilken polyedrisk graf som helst kan realiseras av en konvex polyeder vars koordinater är heltal . Till exempel kan Steinitz ursprungliga induktionsbaserade bevis förstärkas på detta sätt. Heltalen som skulle bli resultatet av Steinitzs konstruktion är dock dubbelt exponentiella i antalet hörn i den givna polyedriska grafen. Att skriva ner tal av denna storlek i binär notation skulle kräva ett exponentiellt antal bitar. Geometriskt betyder detta att vissa egenskaper hos polyedern kan ha storleken dubbelt exponentiellt större än andra, vilket gör realiseringarna som härrör från denna metod problematiska för tillämpningar i grafritning .

Efterföljande forskare har hittat lyftbaserade realiseringsalgoritmer som bara använder ett linjärt antal bitar per vertex. Det är också möjligt att lätta på kravet att koordinaterna är heltal, och tilldela koordinater på ett sådant sätt att $x$ -koordinaterna för hörnen är distinkta heltal i intervallet från 0 till $2n-4$ och de andra två koordinaterna är reella tal i enhetsintervallet , så att varje kant har minst en längd medan den övergripande polyedern har linjär volym. Vissa polyedriska grafer är kända för att kunna realiseras på rutnät av endast polynomstorlek; i synnerhet gäller detta för pyramiderna (förverkliganden av hjulgrafer ), prismor (förverkliganden av prismagrafer ) och staplade polyedrar (förverkliganden av Apolloniska nätverk ).

Ett annat sätt att ange förekomsten av heltalsrealisationer är att varje tredimensionell konvex polyeder har en kombinatoriskt ekvivalent heltalspolyeder. Till exempel är den vanliga dodekaedern inte i sig en heltalspolyeder, på grund av dess regelbundna femkantsytor, men den kan realiseras som en ekvivalent heltalspyritoeder . Detta är inte alltid möjligt i högre dimensioner, där det finns polytoper (som de konstruerade från Perles- konfigurationen ) som inte har någon heltalsekvivalent.

Lika backar

En Halin-graf är ett specialfall av en polyedrisk graf, bildad av ett plant inbäddat träd (utan grader-två hörn) genom att koppla ihop trädets löv till en cykel . För Halin-grafer kan man välja polyedriska realiseringar av en speciell typ: den yttre cykeln bildar en horisontell konvex basyta, och varannan yta ligger direkt ovanför basytan (som i polyedrarna realiserade genom lyft), med alla dessa övre ytor har samma lutning. Polyedriska ytor med lika lutande ytor över vilken baspolygon som helst (inte nödvändigtvis konvex) kan konstrueras från polygonens raka skelett , och ett likvärdigt sätt att beskriva denna insikt är att den tvådimensionella projektionen av trädet på basytan bildar dess raka yta. skelett. Beviset för detta resultat använder induktion: vilket rotat träd som helst kan reduceras till ett mindre träd genom att ta bort löven från en inre nod vars barn alla är löv, Halin-grafen som bildas från det mindre trädet har en realisering genom induktionshypotesen, och det är möjligt att modifiera denna realisering för att lägga till valfritt antal lövbarn till trädnoden vars barn togs bort.

Ange formen på ett ansikte

I vilken polyeder som helst som representerar en given polyedrisk graf ${\displaystyle G} är$ ytorna på $G$ exakt de cykler i $G$ som inte separerar $G$ i två komponenter: det vill säga att ta bort en ansiktscykel från $G$ lämnar resten av $G$ som en ansluten subgraf. Sådana cykler kallas perifera cykler . Således bestäms den kombinatoriska strukturen av ytorna (men inte deras geometriska former) unikt från grafstrukturen. En annan förstärkning av Steinitz sats, av Barnette och Grünbaum, säger att för vilken polyedrisk graf som helst, vilken yta av grafen som helst och vilken konvex polygon som representerar den ytan, är det möjligt att hitta en polyedrisk realisering av hela grafen som har den specificerade formen för det utpekade ansiktet. Detta är relaterat till ett teorem av Tutte, att vilken polyedrisk graf som helst kan ritas i planet med alla ytor konvexa och vilken form som helst för dess yttre yta. Men de plana grafritningarna som produceras med Tuttes metod lyfter inte nödvändigtvis till konvexa polyedrar. Istället bevisar Barnette och Grünbaum detta resultat med en induktiv metod. Det är också alltid möjligt, givet en polyedrisk graf $G$ och en godtycklig cykel $C$ i $G$ , att hitta en realisering för vilken $C$ bildar siluetten av förverkligandet under parallell projektion .

Tangenta sfärer

Förverkligandet av polyedrar med hjälp av cirkelpackningssatsen ger ytterligare en förstärkning av Steinitzs sats: varje 3-kopplad plan graf kan representeras som en konvex polyeder på ett sådant sätt att alla dess kanter tangerar samma enhetssfär , mittsfären av polyeder. Genom att utföra en noggrant vald Möbius-transformation av en cirkelpackning innan den omvandlas till en polyeder, är det möjligt att hitta en polyedrisk realisering som realiserar alla symmetrierna i den underliggande grafen, i den meningen att varje grafautomorfism är en symmetri av den polyedriska realiseringen . Mer generellt, om $G$ är en polyedrisk graf och $K$ är vilken slät tredimensionell konvex kropp som helst , är det möjligt att hitta en polyedrisk representation av $G$ där alla kanter är tangent till $K$ .

Cirkelpackningsmetoder kan också användas för att karakterisera graferna för polyedrar som har en circumsphere genom alla sina hörn, eller en insfär som tangerar alla deras ytor. (Polyedrarna med en circumsphere är också signifikanta i hyperbolisk geometri som de ideala polyedrarna .) I båda fallen är förekomsten av en sfär ekvivalent med lösbarheten av ett system av linjära olikheter på positiva reella variabler associerade med varje kant av grafen. I fallet med insfären måste dessa variabler summeras till exakt en på varje ansiktscykel i grafen och till mer än en för varje icke-ansiktscykel. Dubbelt, för circumsphere, måste variablerna summeras till en vid varje vertex, och mer än en över varje snitt med två eller flera hörn på varje sida av snittet. Även om det kan finnas exponentiellt många linjära olikheter att tillfredsställa, kan en lösning (om en finns) hittas i polynomtid med hjälp av ellipsoidmetoden . Värdena på variablerna från en lösning bestämmer vinklarna mellan par av cirklar i en cirkelpackning vars motsvarande polyeder har den önskade relationen till sin sfär.

Relaterade resultat

Graferna för tredimensionella icke-konvexa polyedrar kanske inte är anslutna (vänster), och även för topologiskt sfäriska polyedrar vars ytor är enkla polygoner kanske dessa grafer inte är 3-anslutna (höger).

I vilken dimension som helst som är högre än tre består det algoritmiska Steinitz-problemet i att bestämma om ett givet gitter är ytgittret av en konvex polytop . Det är osannolikt att det har polynomisk tidskomplexitet, eftersom det är NP-hårt och starkare komplett för den existentiella teorin om verkligheten, även för fyrdimensionella polytoper, enligt Richter-Geberts universalitetsteorem. Här är den existentiella teorin om realerna en klass av beräkningsproblem som kan formuleras i termer av att hitta reella variabler som uppfyller ett givet system av polynomekvationer och olikheter. För det algoritmiska Steinitz-problemet kan variablerna för ett sådant problem vara vertexkoordinaterna för en polytop, och ekvationerna och olikheterna kan användas för att specificera planheten för varje yta i det givna ytgittret och konvexiteten för varje vinkel mellan ytorna. Fullständighet innebär att alla andra problem i denna klass kan omvandlas till en likvärdig instans av det algoritmiska Steinitz-problemet, i polynomtid. Förekomsten av en sådan transformation innebär att, om det algoritmiska Steinitz-problemet har en polynomisk tidslösning, så har varje problem i den existentiella teorin om de verkliga, och varje problem i NP. Men eftersom en given graf kan motsvara mer än ett ytgitter är det svårt att utvidga detta fullständighetsresultat till problemet med att känna igen graferna för 4-polytoper. Att bestämma beräkningskomplexiteten för detta grafigenkänningsproblem är fortfarande öppet.

Forskare har också hittat grafteoretiska karakteriseringar av graferna för vissa speciella klasser av tredimensionella icke-konvexa polyedrar och fyrdimensionella konvexa polytoper. Men i båda fallen förblir det allmänna problemet olöst. Till och med problemet med att bestämma vilka kompletta grafer som är graferna för icke-konvexa polyedrar (andra än $K_{4}$ för tetraedern och $K_{7}$ för Császár-polyedern ) förblir olöst.

Eberhards sats karakteriserar delvis de multiuppsättningar av polygoner som kan kombineras för att bilda ytorna på en konvex polyeder. Det kan bevisas genom att bilda en 3-kopplad plan graf med den givna uppsättningen polygonytor och sedan tillämpa Steinitz sats för att hitta en polyedrisk realisering av den grafen.

László Lovász har visat en överensstämmelse mellan polyedriska representationer av grafer och matriser som realiserar Colin de Verdières grafinvarianter av samma grafer. Colin de Verdière-invarianten är den maximala kornkeringen av en viktad närliggande matris i grafen, under vissa ytterligare förhållanden som är irrelevanta för polyedriska grafer. Dessa är kvadratsymmetriska matriser indexerade av hörnen, med vikten av vertex $i$ i diagonalkoefficienten $M_{i,i}$ och med vikten av kanten ${\ displaystyle i,j}$ i de off-diagonala koefficienterna $M_{i,j}$ och $M_{j,i}$ . När hörn $i$ och $j$ inte är angränsande, måste koefficienten $M_{i,j}$ vara noll Denna invariant är högst tre om och endast om grafen är en plan graf . Som Lovász visar, när grafen är polyedrisk, kan en representation av den som en polyeder erhållas genom att hitta en viktad närliggande matris av kornk tre, hitta tre vektorer som bildar basen för dess nollutrymme, med hjälp av koefficienterna för dessa vektorer som koordinater för hörn på en polyeder, och skala dessa hörn på lämpligt sätt.

Historia

Historien om Steinitz sats beskrivs av Grünbaum (2007) , som noterar dess första framträdande i en kryptisk form i en publikation av Ernst Steinitz , ursprungligen skriven 1916. Steinitz gav mer detaljer i senare föreläsningsanteckningar, publicerade efter hans död 1928. Även om moderna behandlingar av Steinitz sats anger det som en grafteoretisk karakterisering av polyedrar, använde Steinitz inte grafernas språk. Den grafteoretiska formuleringen av satsen introducerades i början av 1960-talet av Branko Grünbaum och Theodore Motzkin , med dess bevis också omvandlat till grafteori i Grünbaums text Convex Polytopes från 1967 . Epifanovs arbete med Δ-Y- och Y-Δ-transformationer, vilket stärkte Steinitzs bevis, motiverades av andra problem än karakteriseringen av polyedrar. Truemper (1989) tillskriver Grünbaum att han observerat relevansen av detta arbete för Steinitzs teorem.

Maxwell-Cremona-överensstämmelsen mellan spänningsdiagram och polyedriska lyftningar utvecklades i en serie artiklar av James Clerk Maxwell från 1864 till 1870, baserad på tidigare arbeten av Pierre Varignon , William Rankine och andra, och populariserades i slutet av 1800-talet av Luigi Cremona . Observationen att denna korrespondens kan användas med Tutte-inbäddningen för att bevisa Steinitzs sats kommer från Eades & Garvan (1995) .

Cirkelpackningssatsen bevisades av Paul Koebe 1936 och (oberoende) av EM Andreev 1970 ; det populariserades i mitten av 1980-talet av William Thurston , som (trots att han citerar Koebe och Andreev) ofta krediteras som en av dess upptäckare. Andreevs version av satsen var redan formulerad som en Steinitz-liknande karaktärisering för vissa polyedrar i hyperboliska rymden , och användningen av cirkelpackning för att realisera polyedrar med mellansfärer kommer från Thurstons arbete. Problemet med att karakterisera polyedrar med inskrivna eller omskrivna sfärer, så småningom löst med en metod baserad på cirkelpackningsförverkliganden, går tillbaka till opublicerade arbeten av René Descartes omkring 1630 och till Jakob Steiner 1832; de första exemplen på polyedrar som inte har någon realisering med en circumsphere eller insphere gavs av Steinitz 1928.