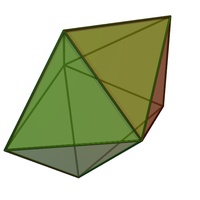
Staplad polytop

I polyedrisk kombinatorik (en gren av matematik) är en staplad polytop en polytop som bildas från en simplex genom att upprepade gånger limma en annan simplex på en av dess facetter .

Exempel

Varje simplex är i sig en staplad polytop.

I tre dimensioner är varje staplad polytop en polyeder med triangulära ytor, och flera av deltaedrarna (polyedrar med liksidiga triangelytor ) är staplade polytoper

Den fyrkantiga tetraedern till vänster är en staplad polytop, men den femkantiga bipyramiden till höger är inte

I en staplad polytop får varje nyligen tillagd simplex endast röra en av de tidigare fasetterna. Så, till exempel, är den fyrade tetraedern, en form som bildas genom att limma samman fem vanliga tetraedrar runt ett gemensamt linjesegment, en staplad polytop (den har ett litet mellanrum mellan den första och sista tetraedern). pentagonala bipyramiden som ser liknande ut är dock inte en staplad polytop, för om den bildas genom att limma ihop tetraedrar, kommer den sista tetraedern att limmas på två triangulära ytor av tidigare tetraedrar istället för bara en.

Andra icke-konvexa staplade deltaedrar inkluderar:

Tre tetraedrar	Fyra tetraedrar	Fem tetraedrar

Kombinatorisk struktur

Ett Apolloniskt nätverk , grafen för en staplad polyeder

Den oriktade grafen som bildas av hörnen och kanterna på en staplad polytop i d- dimensioner är ett ( d + 1)-träd . Närmare bestämt är graferna för staplade polytoper exakt de ( d + 1)-träd där varje d - vertexklick (komplett subgraf) finns i högst två ( d + 1)-vertexklickar. Till exempel är graferna för tredimensionella staplade polyedrar exakt de apolloniska nätverken , graferna som bildas av en triangel genom att upprepade gånger dela upp en triangulär yta av grafen i tre mindre trianglar.

En anledning till betydelsen av staplade polytoper är att bland alla d -dimensionella förenklade polytoper med ett givet antal hörn, har de staplade polytoperna minsta möjliga högre dimensionella ytor. För tredimensionella enkla polyedrar bestäms antalet kanter och tvådimensionella ytor från antalet hörn av Eulers formel , oavsett om polyedern är staplad, men detta är inte sant i högre dimensioner. Analogt är de enkla polytoperna som maximerar antalet högre dimensionella ytor för deras antal hörn de cykliska polytoperna .