Statiska krafter och virtuellt partikelutbyte

Statiska kraftfält är fält, såsom ett enkelt elektriskt , magnetiskt eller gravitationsfält , som existerar utan excitationer. Den vanligaste approximationsmetoden som fysiker använder för spridningsberäkningar kan tolkas som statiska krafter som uppstår från växelverkan mellan två kroppar förmedlade av virtuella partiklar , partiklar som existerar under endast en kort tid bestämt av osäkerhetsprincipen . De virtuella partiklarna, även kända som kraftbärare , är bosoner , med olika bosoner associerade med varje kraft.

Den virtuella partikelbeskrivningen av statiska krafter är kapabel att identifiera krafternas rumsliga form, såsom det omvända kvadratiska beteendet i Newtons lag om universell gravitation och i Coulombs lag . Den kan också förutsäga om krafterna är attraktiva eller frånstötande för liknande kroppar.

Banintegralformuleringen är det naturliga språket för att beskriva kraftbärare . Den här artikeln använder banintegralformuleringen för att beskriva kraftbärarna för spinn 0, 1 och 2 fält. Pioner , fotoner och gravitoner faller inom dessa respektive kategorier.

Det finns gränser för giltigheten av den virtuella partikelbilden. Den virtuella partikelformuleringen är härledd från en metod som kallas störningsteori som är en approximation förutsatt att interaktioner inte är för starka, och var avsedd för att sprida problem, inte bundna tillstånd som atomer. För de starka kraftbindande kvarkarna till nukleoner vid låga energier har störningsteorin aldrig visat sig ge resultat i enlighet med experiment, så giltigheten av den "kraftförmedlande partikelbilden" är tveksam. På liknande sätt misslyckas metoden för bundna tillstånd . I dessa fall måste den fysiska tolkningen omprövas. Som ett exempel kunde beräkningarna av atomstruktur i atomfysik eller av molekylstruktur i kvantkemi inte lätt upprepas, om alls, med hjälp av den "kraftförmedlande partikelbilden".

Användning av den "kraftförmedlande partikelbilden" (FMPP) är onödig i icke-relativistisk kvantmekanik , och Coulombs lag används som ges i atomfysik och kvantkemi för att beräkna både bundna och spridningstillstånd. En icke-perturbativ relativistisk kvantteori , där Lorentz-invariansen bevaras, kan uppnås genom att utvärdera Coulombs lag som en 4-rymdsinteraktion med hjälp av 3-rumspositionsvektorn för en referenselektron som lyder Diracs ekvation och kvantbanan för en andra elektron som beror bara på den skalade tiden. Kvantbanan för varje elektron i en ensemble härleds från Dirac-strömmen för varje elektron genom att sätta den lika med ett hastighetsfält gånger en kvantdensitet, beräkna ett positionsfält från tidsintegralen för hastighetsfältet och slutligen beräkna en kvantbana från positionsfältets förväntade värde. Kvantbanorna är naturligtvis spinnberoende, och teorin kan valideras genom att kontrollera att Paulis uteslutningsprincip följs för en samling fermioner .

Klassiska krafter

Kraften som en massa utövar på en annan och kraften som en laddning utövar på en annan är slående lika. Båda faller av som kvadraten på avståndet mellan kropparna. Båda är proportionella mot produkten av kropparnas egenskaper, massa vid gravitation och laddning vid elektrostatik.

De har också en slående skillnad. Två massor attraherar varandra, medan två lika laddningar stöter bort varandra.

I båda fallen verkar kropparna agera på varandra på avstånd. Begreppet fält uppfanns för att förmedla interaktionen mellan kroppar och därmed eliminera behovet av agerande på distans . Gravitationskraften förmedlas av gravitationsfältet och Coulombkraften förmedlas av det elektromagnetiska fältet .

Gravitationskraften

Gravitationskraften på en massa $m$ som utövas av en annan massa $\displaystyle M}$ { är

$$\mathbf {F} =-G{\frac {mM}{r^{2}}}\,{\hat {\mathbf {r} }}=m\mathbf {g} \left(\mathbf {r} \right),$$

där G är gravitationskonstanten , r är avståndet mellan massorna och ${\hat {\mathbf {r} }}$ är enhetsvektorn från massa $M$ till massa ${\ displaystil m}$ .

Kraften kan också skrivas

$$\mathbf {F} =m\mathbf {g} \left(\mathbf {r} \right),$$

där $\mathbf {g} \left(\mathbf {r} \right)$ är gravitationsfältet som beskrivs av fältekvationen

$$\nabla \cdot \mathbf {g} =-4\pi G\rho _{m},$$

där $\rho _{m}$ är masstätheten vid varje punkt i rymden.

Coulomb kraft

Den elektrostatiska Coulomb-kraften på en laddning $q$ som utövas av en laddning $Q$ är ( SI-enheter )

$$\mathbf {F} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {qQ}{r^{ 2}}}\mathbf {\hat {r}} ,$$

där $\varepsilon _{0}$ är vakuumpermittiviteten , $r$ är separationen av de två laddningarna och $\mathbf {\hat {r}}$ är en enhet vektor i riktningen från laddning $Q$ till laddning $q$ .

Coulomb-kraften kan också skrivas i termer av ett elektrostatiskt fält :

$$\mathbf {F} =q\mathbf {E} \left(\mathbf {r} \right),$$

var

$$\nabla \cdot \mathbf {E} ={\frac {\rho _{q}}{\varepsilon _{0}}};$$

$\rho _{q}$ är laddningstätheten vid varje punkt i rymden.

Virtuellt partikelutbyte

I störningsteorin genereras krafter genom utbyte av virtuella partiklar . Mekaniken för utbyte av virtuella partiklar beskrivs bäst med vägintegralformuleringen av kvantmekanik. Det finns dock insikter som kan erhållas utan att gå in på banintegralernas maskineri, som varför klassiska gravitationskrafter och elektrostatiska krafter faller av som den omvända kvadraten på avståndet mellan kroppar.

Path-integral formulering av virtuell-partikelutbyte

En virtuell partikel skapas av en störning av vakuumtillståndet , och den virtuella partikeln förstörs när den absorberas tillbaka till vakuumtillståndet av en annan störning. Störningarna föreställs bero på kroppar som interagerar med den virtuella partikelns fält.

Sannolikhetsamplituden

Med hjälp av naturliga enheter , ${\displaystyle \hbar =c=1} ,$ ges sannolikhetsamplituden för skapandet, fortplantningen och förstörelsen av en virtuell partikel, i vägintegralformuleringen av

$$Z\equiv \langle 0|\exp \left(-i{\hat {H}}T\right)|0\rangle =\exp \left(-iET\right)=\int D\varphi \;\exp \left(i{\mathcal {S}}[\varphi ]\right )\;=\exp \left(iW\right)$$

där ${\hat {H}}$ är Hamiltons operator , $T$ är förfluten tid, $E$ är energiförändringen på grund av störningen, ${ \displaystyle W=-ET}$ är förändringen i handlingen på grund av störningen, $\varphi$ är fältet för den virtuella partikeln, integralen är över alla banor, och den klassiska handlingen ges av

$${\mathcal {S}}[\varphi ]=\int \mathrm {d} ^{4}x\;{{\mathcal { L}}[\varphi (x)]\,}$$

där ${\mathcal {L}}[\varphi (x)]$ är lagrangisk densitet.

Här ges rumtidsmåttet av

$$\eta _{\mu \nu }={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}.$$

Banintegralen kan ofta konverteras till formen

$$Z=\int \exp \left[i\int d^{4}x\left({ \frac {1}{2}}\varphi {\hat {O}}\varphi +J\varphi \right)\right]D\varphi$$

där ${\hat {O}}$ är en differentialoperator med $\varphi$ och $J$ funktioner för rumtid . Den första termen i argumentet representerar den fria partikeln och den andra termen representerar störningen av fältet från en extern källa såsom en laddning eller en massa.

Integralen kan skrivas (se Vanliga integraler i kvantfältteori § Integraler med differentialoperatorer i argumentet )

$$Z\propto \exp \left(iW\left(J\right)\right)$$

var

$$W\left(J\right)=-{\frac {1}{2 }}\iint d^{4}x\;d^{4}y\;J\left(x\right)D\left(xy\right)J\left(y\right)$$

är förändringen i åtgärden på grund av störningarna och propagatorn D $\displaystyle D\left(xy\right)}$ är lösningen på

$${\hat {O}}D\left(xy\right)=\delta ^{4}\left(xy\right).$$

Energi av interaktion

Vi antar att det finns två punktstörningar som representerar två kroppar och att störningarna är orörliga och konstanta i tiden. Störningarna kan skrivas

$$J(x)=\left(J_{1}+J_{2},0,0,0\right)$$

$$J_{1}=a_{1}\delta ^{3}\left({\vec {x}}-{\vec {x} }_{1}\right)$$

$$J_{2}=a_{2}\delta ^{3}\left({\vec {x}}-{\vec {x} }_{2}\right)$$

där deltafunktionerna finns i rymden, är störningarna placerade vid ${\vec {x}}_{1}$ och ${\vec {x}}_{2}$ , och koefficienterna $a_{1}$ och $a_{2}$ är styrkorna hos störningarna.

Om vi ​​försummar självinteraktioner av störningarna så blir W

$$W\left(J\ höger)=-\iint d^{4}x\;d^{4}y\;J_{1}\left(x\right){\frac {1}{2}}\left[D\left( xy\right)+D\left(yx\right)\right]J_{2}\left(y\right),$$

som kan skrivas

$$W\left(J\right)=-Ta_{1}a_{2}\int {\frac {d^{3}k}{(2\pi )^{3}}}\;\; D\left(k\right)\mid _{k_{0}=0}\;\exp \left(i{\vec {k}}\cdot \left({\vec {x}}_{1} -{\vec {x}}_{2}\right)\right).$$

Här är $D\left(k\right)$ Fouriertransformen av

$${\frac {1}{2}}\left[D\left(xy\right)+D\left(yx\right)\right].$$

Slutligen är förändringen i energi på grund av de statiska störningarna i vakuumet

$$E=-{\frac {W}{T}}=a_{1}a_{2}\int {\frac {d^{3}k}{(2\pi )^{3}}} \;\;D\left(k\right)\mid _{k_{0}=0}\;\exp \left(i{\vec {k}}\cdot \left({\vec {x}} _{1}-{\vec {x}}_{2}\right)\right).$$

Om denna kvantitet är negativ är kraften attraktiv. Om den är positiv är kraften frånstötande.

Exempel på statiska, orörliga, interagerande strömmar är Yukawa-potentialen , Coulomb-potentialen i ett vakuum och Coulomb-potentialen i en enkel plasma eller elektrongas .

Uttrycket för interaktionsenergin kan generaliseras till den situation där punktpartiklarna rör sig, men rörelsen är långsam jämfört med ljusets hastighet. Exempel är Darwin-interaktionen i ett vakuum och i ett plasma .

Slutligen kan uttrycket för interaktionsenergin generaliseras till situationer där störningarna inte är punktpartiklar, utan möjligen är linjeladdningar, laddningsrör eller strömvirvlar. Exempel inkluderar: två linjeladdningar inbäddade i en plasma eller elektrongas , Coulomb-potential mellan två strömslingor inbäddade i ett magnetfält och den magnetiska interaktionen mellan strömslingor i en enkel plasma eller elektrongas . Som framgår av Coulomb-interaktionen mellan laddningsrör, som visas nedan, kan dessa mer komplicerade geometrier leda till sådana exotiska fenomen som bråkdelar av kvanttal .

Utvalda exempel

Yukawa-potentialen: Kraften mellan två nukleoner i en atomkärna

Betrakta spinn -0 Lagrangian densitet

$${\mathcal {L}}[\varphi (x)]={\frac {1}{2}}\left[\left(\partial \varphi \right)^{2}-m^{2 }\varphi ^{2}\right].$$

Rörelseekvationen för denna Lagrangian är Klein–Gordon-ekvationen

$$\partial ^{2}\varphi +m^{2}\varphi =0.$$

Om vi ​​lägger till en störning blir sannolikhetsamplituden

$$Z=\int D\varphi \;\exp \left\{i\int d^{4}x\;\left[{\frac {1}{2}}\left(\left(\partial \varphi \right)^{2}-m^{2}\varphi ^{2}\right)+J\varphi \right]\right\}.$$

Om vi ​​integrerar med delar och försummar gränstermer i oändligheten blir sannolikhetsamplituden

$$Z=\int D\varphi \;\exp \left\{i\int d^{4}x\;\left[-{\frac {1}{2}}\varphi \left(\partial ^{2}+m^{2}\right)\varphi +J\varphi \right]\right\}.$$

Med amplituden i denna form kan man se att propagatorn är lösningen på

$$-\left(\partial ^{2}+m^{2}\right)D\left(xy\right)=\delta ^{4}\left(xy\right).$$

Av detta kan man se att

$$D\left(k\right)\mid _{k_{0}=0}\;=\;-{\frac {1}{{\vec {k}}^{2}+m^{ 2}}}.$$

Energin på grund av de statiska störningarna blir (se Vanliga integraler i kvantfältteori § Yukawa Potential: Coulomb-potentialen med massa )

$$E=-{\frac {a_{1}a_{2}}{4\pi r}}\exp \left(-mr \höger)$$

med

$$r^{2}=\left({\vec {x}}_{1}-{\vec {x}}_{2}\right )^{2}$$

som är attraktiv och har ett utbud av

$${\frac {1}{m}}.$$

Yukawa föreslog att detta fält beskriver kraften mellan två nukleoner i en atomkärna. Det gjorde det möjligt för honom att förutsäga både räckvidden och massan av partikeln, nu känd som pion , som är associerad med detta fält.

Elektrostatik

Coulomb-potentialen i ett vakuum

Betrakta snurran -1 Proca Lagrangian med en störning

$${\mathcal {L}}[\varphi (x)]=- {\frac {1}{4}}F_{\mu \nu }F^{\mu \nu}+{\frac {1}{2}}m^{2}A_{\mu }A^{\ mu }+A_{\mu }J^{\mu }$$

var

$$F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu } ,$$

laddningen är bevarad

$$\partial _{\mu }J^{\mu }=0,$$

och vi väljer Lorenz-mätaren

$$\partial _{\mu }A^{\mu }=0.$$

Dessutom antar vi att det bara finns en tidsliknande komponent $J^{0}$ till störningen. I vanligt språk betyder det att det finns en laddning vid störningspunkterna, men det finns inga elektriska strömmar.

Om vi ​​följer samma procedur som vi gjorde med Yukawa-potentialen finner vi det

$${\begin{aligned}&-{\frac {\frac }{4}}\int d^{4}xF_{\mu \nu}F^{\mu \nu}=-{\frac {1}{4}}\int d^{4}x\left( \partial _{\mu }A_{\nu}-\partial _{\nu}A_{\mu}\right)\left(\partial ^{\mu }A^{\nu}-\partial ^{\ nu }A^{\mu }\right)\\={}&{\frac {1}{2}}\int d^{4}x\;A_{\nu }\left(\partial ^{2 }A^{\nu}-\partial ^{\nu}\partial _{\mu}A^{\mu }\right)={\frac {1}{2}}\int d^{4}x \;A^{\mu }\left(\eta _{\mu \nu}\partial ^{2}\right)A^{\nu},\end{aligned}}$$

vilket innebär

$$\eta _{\mu \alpha }\left(\partial ^{2} +m^{2}\right)D^{\alpha \nu}\left(xy\right)=\delta _{\mu }^{\nu}\delta ^{4}\left(xy\right)$$

och

$$D_{\mu \nu }\left(k\right)\mid _{k_{0}=0}\;=\;\eta _{\mu \nu }{\frac {1}{- k^{2}+m^{2}}}.$$

Detta ger

$$D\left(k\right)\mid _{k_{0}=0}\;=\;{\frac {1}{{ \vec {k}}^{2}+m^{2}}}$$

för den tidslika förökaren och

$$E=+{\frac {a_{1}a_{2}}{4\pi r}}\exp \left(-mr \höger)$$

som har motsatt tecken till Yukawa-fallet.

Inom gränsen för noll fotonmassa reduceras Lagrangian till Lagrangian för elektromagnetism

$$E={\frac {a_{1}a_{2}}{4\pi r}}.$$

Därför minskar energin till den potentiella energin för Coulomb-kraften och koefficienterna $a_{1}$ och $a_{2}$ är proportionella mot den elektriska laddningen. Till skillnad från Yukawa-fallet avvisar liksom kroppar varandra i detta elektrostatiska fall.

Coulombpotential i en enkel plasma- eller elektrongas

Plasmavågor

Dispersionsrelationen för plasmavågor är _

$$\omega ^{2}=\omega _{p}^{2}+\gamma \left(\omega \right){\frac {T_{e}}{m}}{\vec {k} }^{2}.$$

där $\omega$ är vågens vinkelfrekvens,

$$\omega _{p}^{2}={\frac {4\pi ne^{2}}{m}}$$

är plasmafrekvensen , $e$ är storleken på elektronladdningen , $\displaystyle m}$ { är elektronmassan , $T_{e}$ är elektrontemperaturen ( Boltzmanns konstant lika med ett ), och $\gamma \left(\omega \right)$ är en faktor som varierar med frekvensen från ett till tre. Vid höga frekvenser, i storleksordningen av plasmafrekvensen, är kompressionen av elektronvätskan en adiabatisk process och $\gamma \left(\omega \right)$ är lika med tre. Vid låga frekvenser är komprimeringen en isoterm process och $\gamma \left(\omega \right)$ är lika med ett. Retardationseffekter har försummats vid erhållande av plasma-vågspridningsförhållandet.

För låga frekvenser blir dispersionsrelationen

$${\vec {k}}^{2}+{\vec {k}}_{D}^{2}=0$$

var

$$k_{D}^{2}={\frac {4\pi ne^{2}}{T_{e}}}$$

är Debye-talet, vilket är inversen av Debye-längden . Detta tyder på att propagatorn är det

$$D\left(k\right)\mid _{k_{0}=0}\;=\;{\frac {1}{{\vec {k}}^{2}+k_{D} ^{2}}}.$$

Faktum är att om retardationseffekterna inte försummas, så är spridningsrelationen det

$$-k_{0}^{2}+{\vec {k}}^{2}+k_{D}^{ 2}-{\frac {m}{T_{e}}}k_{0}^{2}=0,$$

vilket verkligen ger den gissade propagatorn. Denna propagator är densamma som den massiva Coulomb-propagatorn med massan lika med den omvända Debye-längden. Interaktionsenergin är därför

$$E={\frac {a_{1}a_{2}}{4\pi r}}\exp \left(-k_{D}r\right).$$

Coulomb-potentialen screenas på längdskalor av en Debye-längd.

Plasmoner

I en kvantelektrongas är plasmavågor kända som plasmoner . Debye screening ersätts med Thomas–Fermi screening för att ge

$$E={\frac {a_{1}a_{2}}{4\pi r}}\exp \left(-k_{ s}r\right)$$

där inversen av Thomas–Fermi-screeningslängden är

$$k_{s}^{2}={\frac {6\pi ne^{2}}{\varepsilon _{F}}}$$

och $displaystyle \varepsilon _{F}}$${\textstyle \varepsilon _{F}={\frac {\hbar ^{2}}{2m}}\left({3\pi ^{2}n}\right)^{2/3}.}$ är Fermi-energin

Detta uttryck kan härledas från den kemiska potentialen för en elektrongas och från Poissons ekvation . Den kemiska potentialen för en elektrongas nära jämvikt är konstant och ges av

$$\mu =-e\varphi +\varepsilon _{F}$$

där $\varphi$ är den elektriska potentialen . Linjärisering av Fermi-energin till första ordningen i densitetsfluktuationen och kombination med Poissons ekvation ger skärmningslängden. Kraftbäraren är kvantversionen av plasmavågen .

Två linjeladdningar inbäddade i en plasma- eller elektrongas

Vi betraktar en laddningslinje med axel i z -riktningen inbäddad i en elektrongas

$$J_{1}\left(x\right)={\frac {a_{1}}{L_{B}}} {\frac {1}{2\pi r}}\delta ^{2}\left(r\right)$$

där $r$ är avståndet i xy -planet från laddningslinjen, $L_{B}$ är materialets bredd i z-riktningen. Den övre skriften 2 indikerar att Dirac delta-funktionen är i två dimensioner. Förökaren är

$$D\left(k\right)\mid _{k_{0}=0}\;=\;{\frac {1} {{\vec {k}}^{2}+k_{Ds}^{2}}}$$

där $k_{Ds}$ är antingen den inversa Debye–Hückel screeningslängden eller den inversa Thomas–Fermi screeninglängden .

Interaktionsenergin är

$${ \displaystyle E=\left({\frac {a_{1}\,a_{2}}{2\pi L_{B}}}\right)\int _{0}^{\infty }{\frac { k\,dk}{k^{2}+k_{Ds}^{2}}}{\mathcal {J}}_{0}(kr_{12})=\left({\frac {a_{1 }\,a_{2}}{2\pi L_{B}}}\right)K_{0}\left(k_{Ds}r_{12}\right)}$$

där ${\mathcal {J}}_{n}(x)$ och $K_{0}(x)$ är Bessel-funktioner och $r_ {12}$ är avståndet mellan de två linjeladdningarna. För att erhålla interaktionsenergin använde vi integralerna (se Vanliga integraler i kvantfältteori § Integration av den cylindriska propagatorn med massa )

$$\int _{0}^{2\pi }{\frac {d\varphi }{2\pi }}\exp \left(ip\cos \left(\varphi \right)\right)={\mathcal {J}}_{0}(p)$$

och

$$\int _{0}^{\infty }{\frac {k\,dk}{k^{2}+m^{2}}}{\mathcal {J}}_{0}(kr )=K_{0}(mr).$$

För $k_{Ds}r_{12}\ll 1$ har vi

$$K_{0}\left(k_{Ds}r_{12}\right)\rightarrow -\ln \left({\frac {k_{Ds}r_{12}}{2}}\right)+ 0,5772.$$

Coulombpotential mellan två strömslingor inbäddade i ett magnetfält

Interaktionsenergi för virvlar

Vi betraktar en laddningstäthet i rör med axel längs ett magnetfält inbäddat i en elektrongas

$$J_{1}\left(x\right)={\frac {a_{1}}{L_{ b}}}{\frac {1}{2\pi r}}\delta ^{2}{\left(r-r_{B1}\right)}$$

där $r$ är avståndet från styrcentrum , $L_{B}$ är materialets bredd i magnetfältets riktning

$$r_{B1}={\frac {{\sqrt {4\pi }}m_{1}v_{1}} {a_{1}B}}={\sqrt {\frac {2\hbar }{m_{1}\omega _{c}}}}$$

där cyklotronfrekvensen är ( gaussiska enheter )

$$\omega _{c}={\frac {a_{1}B}{{\sqrt {4\pi }}m_{1}c}}$$

och

$$v_{1}={\sqrt {\frac {2\hbar \omega _{c}}{m_{1}}}}$$

är partikelns hastighet runt magnetfältet, och B är storleken på magnetfältet. Hastighetsformeln kommer från att sätta den klassiska kinetiska energin lika med avståndet mellan Landau-nivåerna i kvantbehandlingen av en laddad partikel i ett magnetfält.

I denna geometri kan interaktionsenergin skrivas

$$E=\left({\frac {a_{1}\,a_{2}}{2\pi L_{B}}}\right)\int _{0}^{\infty }{k\;dk\ ;}D\left(k\right)\mid _{k_{0}=k_{B}=0}{\mathcal {J}}_{0}\left(kr_{B1}\right){\mathcal {J}}_{0}\left(kr_{B2}\right){\mathcal {J}}_{0}\left(kr_{12}\right)$$

där $r_{12}$ är avståndet mellan mitten av de nuvarande slingorna och ${\mathcal {J}}_{n}(x)$ är en Bessel-funktion av den första sorten. För att erhålla interaktionsenergin använde vi oss av integralen

$$\int _{0}^{2\pi }{\frac {d\varphi }{2\pi }}\exp \left(ip\cos(\varphi )\right)={\mathcal {J }}_{0}(p).$$

Elektriskt fält på grund av en densitetsstörning

Den kemiska potentialen nära jämvikt, ges av

$$\mu =-e\varphi +N\hbar \omega _{c}=N_{0}\hbar \omega _{c}$$

där $-e\varphi$ är den potentiella energin för en elektron i en elektrisk potential och $N_{0}$ och $N$ är antalet partiklar i elektrongasen i frånvaron av och i närvaro av en elektrostatisk potential, respektive.

Densitetsfluktuationen är då

$$\delta n={\frac {e\varphi }{\hbar \omega _{c}A_{M}L_{B}}}$$

där $A_{M}$ är arean av materialet i planet vinkelrätt mot magnetfältet.

Poissons ekvation ger

$$\left(k^{2}+k_{B}^{2}\right)\varphi =0$$

var

$$k_{B}^{2}={\frac {4\pi e^{2}}{\hbar \omega _{c}A_{M}L_{B}}}.$$

Förökaren är då

$$D\left(k\right)\mid _{k_{0}=k_{B}=0}={\frac { 1}{k^{2}+k_{B}^{2}}}$$

och interaktionsenergin blir

$$E=\left({\frac {a_{1}\,a_{2} }{2\pi L_{B}}}\right)\int _{0}^{\infty }{\frac {k\;dk\;}{k^{2}+k_{B}^{2 }}}{\mathcal {J}}_{0}\left(kr_{B1}\right){\mathcal {J}}_{0}\left(kr_{B2}\right){\mathcal {J }}_{0}\left(kr_{12}\right)=\left({\frac {2e^{2}}{L_{B}}}\right)\int _{0}^{\infty }{\frac {k\;dk\;}{k^{2}+k_{B}^{2}r_{B}^{2}}}{\mathcal {J}}_{0}^{ 2}\left(k\right){\mathcal {J}}_{0}\left(k{\frac {r_{12}}{r_{B}}}\right)$$

där vi i den andra likheten ( Gaussiska enheter ) antar att virvlarna hade samma energi och elektronladdning.

I analogi med plasmoner är kraftbäraren kvantversionen av den övre hybridoscillationen som är en longitudinell plasmavåg som utbreder sig vinkelrätt mot magnetfältet .

Strömmar med vinkelmomentum

Deltafunktionsströmmar

Figur 1. Interaktionsenergi vs. r för rörelsemängdstillstånd av värde ett. Kurvorna är identiska med dessa för alla värden på $l=l'$ . Längder är i enheter är i $r_{l}$ , och energin är i enheter av ${\textstyle {\frac {e^{2}}{L_{B}}}}$ . Här $r=r_{12}$ . Observera att det finns lokala minima för stora värden på $k_{B}$ .

Figur 2. Interaktionsenergi mot r för rörelsemängdstillstånd av värde ett och fem.

Figur 3. Interaktionsenergi mot r för olika värden på theta. Den lägsta energin är för ${\textstyle \theta ={\frac {\pi }{4}}}$ eller ${\frac {l}{l'}}=1$ . Den högsta energin som plottas är för ${\textstyle \theta =0,90{\frac {\pi }{4}}}$ . Längder är i enheter av $r_{ll'}$ .

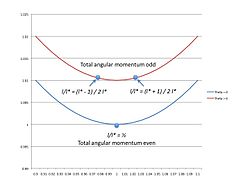
Figur 4. Jordtillståndsenergier för jämna och udda värden på vinkelmoment. Energi plottas på den vertikala axeln och r plottas på den horisontella. När den totala rörelsemängden är jämn, uppstår energiminimum när $l=l'$ eller ${\textstyle {\frac {l}{l^{*}}}= {\frac {1}{2}}}$ . När det totala vinkelmomentet är udda, finns det inga heltalsvärden för vinkelmomentet som kommer att ligga inom energiminimum. Därför finns det två tillstånd som ligger på vardera sidan av minimumet. Eftersom $l\neq l'$ är den totala energin högre än fallet när $l=l'$ för ett givet värde på $l^{* }$ .

Till skillnad från klassiska strömmar kan kvantströmslingor ha olika värden på Larmor-radien för en given energi. Landau-nivåer , energitillstånden för en laddad partikel i närvaro av ett magnetiskt fält, är flerfaldigt degenererade . Strömslingorna motsvarar rörelsemängdstillstånden hos den laddade partikeln som kan ha samma energi. Specifikt är laddningstätheten toppad runt radier av

$$r_{l}={\sqrt {l}}\;r_{B}\;\;\;l=0,1,2,\ ldots$$

där ${\displaystyle l} är$ kvanttalet för vinkelmomentet . När $l=1$ återställer vi den klassiska situationen där elektronen kretsar runt magnetfältet vid Larmor-radien . Om strömmar med två vinkelmoment $l>0$ och $l'\geq l$ samverkar, och vi antar att laddningstätheterna är deltafunktioner vid radien $r_{l }$ , då är interaktionsenergin

$$E=\left({\frac {2e^{2}}{L_{B}}}\right)\int _{0}^{\infty }{\frac {k\;dk\;} {k^{2}+k_{B}^{2}r_{l}^{2}}}\;{\mathcal {J}}_{0}\left(k\right)\;{\mathcal {J}}_{0}\left({\sqrt {\frac {l'}{l}}}\;k\right)\;{\mathcal {J}}_{0}\left(k{ \frac {r_{12}}{r_{l}}}\right).$$

Interaktionsenergin för $l=l'$ ges i figur 1 för olika värden på $k_{B}r_{l}$ . Energin för två olika värden anges i figur 2.

Kvasipartiklar

För stora värden på rörelsemängd kan energin ha lokala minima på andra avstånd än noll och oändlighet. Det kan verifieras numeriskt att minima inträffar vid

$$r_{12}=r_{ll'}={\sqrt {l+l'}}\;r_{B}.$$

Detta antyder att paret av partiklar som är bundna och åtskilda av ett avstånd $r_{ll'}$ fungerar som en enda kvasipartikel med rörelsemängd $l+l'$ .

Om vi ​​skalar längderna som $r_{ll'}$ så blir interaktionsenergin

$$E={\frac {2e^{2}}{L_{B}}}\int _{0}^{\infty }{\frac {k\,dk}{k^{2}+k_{B} ^{2}r_{ll'}^{2}}}\;{\mathcal {J}}_{0}\left(\cos \theta \,k\right)\;{\mathcal {J}} _{0}(\sin \theta \,k)\;{\mathcal {J}}_{0}{\left(k{\frac {r_{12}}{r_{ll'}}}\right )}$$

var

$$\tan \theta ={\sqrt {\frac {l}{l'}}}.$$

Värdet på $r_{12}$ där energin är minimum, ${\displaystyle r_{12}=r_{ll'}} ,$ är oberoende av förhållandet ${\textstil \tan \theta ={\sqrt {{l}/{l'}}}}$ . Men värdet av energin som minimum beror på förhållandet. Det lägsta energiminimum inträffar när

$${\frac {l}{l'}}=1.$$

När förhållandet skiljer sig från 1 är energiminimumet högre (Figur 3). Därför, för jämna värden på totalt momentum, uppstår den lägsta energin när (Figur 4)

$$l=l'=1$$

eller

$${\frac {l}{l^{*}}}={\frac {1}{2}}$$

där den totala rörelsemängden skrivs som

$$l^{*}=l+l'.$$

När den totala rörelsemängden är udda kan minima inte inträffa för $l=l'.$ De lägsta energitillstånden för udda total rörelsemängd uppstår när

$${\frac {l}{l^{*}}}=\;{\frac {l^{*}\pm 1}{2l^{*} }}$$

eller

$${\frac {l}{l^{*}}}={\frac {1}{3}},{\frac {2 }{5}},{\frac {3}{7}},{\text{etc.,}}$$

och

$${\frac {l}{l^{*}}}={\frac {2}{3}},{\frac {3 }{5}},{\frac {4}{7}},{\text{etc.,}}$$

som också visas som serier för fyllnadsfaktorn i fraktionell kvant Hall-effekt .

Laddningsdensitet spridd över en vågfunktion

Laddningsdensiteten är faktiskt inte koncentrerad till en deltafunktion. Laddningen sprids över en vågfunktion. I så fall är elektrondensiteten

$${\frac {1}{\pi r_{B}^{2}L_{B}}}{\frac {1}{n!}}\left({\frac {r}{r_{B }}}\right)^{2l}\exp \left(-{\frac {r^{2}}{r_{B}^{2}}}\right).$$

Interaktionsenergin blir

$$E=\left({\frac {2e^{2}}{L_{B}}}\right)\int _{0}^{\infty }{\frac {k\;dk\;}{k^{2}+k_{B}^{2}r_{B}^{2}}}\;M{\left(l+1,1,-{\frac {k^{2}}{4}}\right)}\;M{\left(l'+1,1,-{\frac {k^{2}}{4}}\right)}\; {\mathcal {J}}_{0}{\left(k{\frac {r_{12}}{r_{B}}}\right)}$$

där $M$ är en konfluent hypergeometrisk funktion eller Kummer-funktion . För att erhålla interaktionsenergin har vi använt integralen (se Vanliga integraler i kvantfältteori § Integration över en magnetisk vågfunktion )

$${\frac {2}{n!}}\int _{0}^{\infty }dr\;r^{2n+1}\exp \left(-r^{2}\right)J_ {0}(kr)=M\left(n+1,1,-{\frac {k^{2}}{4}}\right).$$

Liksom med deltafunktionsladdningar beror värdet på $r_{12}$ där energin är ett lokalt minimum endast på det totala rörelsemängdsrörelsen, inte på de individuella strömmarnas vinkelmoment. Liksom med deltafunktionsladdningarna ökar också energin vid minimum när förhållandet mellan vinkelmoment varierar från ett. Därför serien

$${\frac {l}{l^{*}}}={\frac {1}{3}},{\frac {2 }{5}},{\frac {3}{7}},{\text{etc.,}}$$

och

$${\frac {l}{l^{*}}}={\frac {2}{3}},{\frac {3 }{5}},{\frac {4}{7}},{\text{etc.,}}$$

förekommer också i fallet med laddningar som sprids av vågfunktionen.

Laughlin -vågfunktionen är en ansats för kvasipartikelvågfunktionen. Om väntevärdet för interaktionsenergin tas över en Laughlin-vågfunktion bevaras även dessa serier.

Magnetostatik

Darwin interaktion i ett vakuum

En laddad rörlig partikel kan generera ett magnetfält som påverkar rörelsen hos en annan laddad partikel. Den statiska versionen av denna effekt kallas Darwininteraktionen . För att beräkna detta, överväga de elektriska strömmarna i rymden som genereras av en rörlig laddning

$${\vec {J}}_{1}{\left({\vec {x}}\right )}=a_{1}{\vec {v}}_{1}\delta ^{3}{\left({\vec {x}}-{\vec {x}}_{1}\right) }$$

med ett jämförbart uttryck för ${\vec {J}}_{2}$ .

Fouriertransformen av denna ström är

$${\vec {J}}_{1}{\left({\vec {k}}\right)}=a_{1}{\vec {v}}_{1}\exp \left( i{\vec {k}}\cdot {\vec {x}}_{1}\right).$$

Strömmen kan sönderdelas i en tvärgående och en längsgående del (se Helmholtz-nedbrytning ) .

$${\vec {J}}_{1}{\left({\vec {k}}\right)}=a_{1}\left[1-{\hat {k}}{\hat { k}}\right]\cdot {\vec {v}}_{1}\exp \left(i{\vec {k}}\cdot {\vec {x}}_{1}\right)+a_ {1}\left[{\hat {k}}{\hat {k}}\right]\cdot {\vec {v}}_{1}\exp \left(i{\vec {k}}\ cdot {\vec {x}}_{1}\right).$$

Hatten indikerar en enhetsvektor . Den sista termen försvinner pga

$${\vec {k}}\cdot {\vec {J}}=-k_{0}J^{0}\rightarrow 0,$$

som är resultatet av laddningskonservering. Här $k_{0}$ eftersom vi överväger statiska krafter.

Med strömmen i denna form kan interaktionsenergin skrivas

$$E=a_{1}a_{2}\int {\frac {d^{3}k}{(2\pi )^{3}}}\;\;D\left(k\right) \mid _{k_{0}=0}\;{\vec {v}}_{1}\cdot \left[1-{\hat {k}}{\hat {k}}\right]\cdot {\vec {v}}_{2}\;\exp \left(i{\vec {k}}\cdot \left(x_{1}-x_{2}\right)\right).$$

Propagatorekvationen för Proca Lagrangian är

$$\eta _{\mu \alpha }\left(\partial ^{2}+m^{2}\right)D^{\alpha \nu}\left(xy\right)=\delta _{ \mu }^{\nu }\delta ^{4}\left(xy\right).$$

Den rymdliknande lösningen är

$$D\left(k\right)\mid _{k_{0}=0}\;=\;-{\frac {1 }{{\vec {k}}^{2}+m^{2}}},$$

Vilket ger

$$E=-a_{1}a_{2}\int {\frac {d^{3}k}{(2\pi )^{3}}}\;\;{\frac { {\vec {v}}_{1}\cdot \left[1-{\hat {k}}{\hat {k}}\right]\cdot {\vec {v}}_{2}}{ {\vec {k}}^{2}+m^{2}}}\;\exp \left(i{\vec {k}}\cdot \left(x_{1}-x_{2}\right )\höger)$$

som utvärderar till (se Vanliga integraler i kvantfältteori § Tvärpotential med massa )

$$E=-{\frac {1}{2}}{\frac {a_{1}a_{2}}{4\pi r}}e^{-mr}\left\{{\frac {2}{\left(mr\right)^{2}}}\left(e^{mr}-1\right)-{\frac {2}{mr}}\right\}{\vec {v }}_{1}\cdot \left[1+{\hat {r}}{\hat {r}}\right]\cdot {\vec {v}}_{2}$$

som reducerar till

$$E=-{\frac {1}{2}}{\frac {a_{ 1}a_{2}}{4\pi r}}{\vec {v}}_{1}\cdot \left[1+{\hat {r}}{\hat {r}}\right]\ cdot {\vec {v}}_{2}$$

inom gränsen för små m . Interaktionsenergin är det negativa av interaktionen Lagrangian. För två lika partiklar som rör sig i samma riktning är interaktionen attraktiv, vilket är motsatsen till Coulomb-interaktionen.

Darwin interaktion i ett plasma

I ett plasma är dispersionsrelationen för en elektromagnetisk våg ( $c=1$ )

$$k_{0}^{2}=\omega _{p}^{2}+{\vec {k}}^{2},$$

vilket innebär

$$D\left(k\right)\mid _{k_{0}=0}\;=\;-{\frac {1}{{\vec {k}}^{2}+\omega _ {p}^{2}}}.$$

Här är $\omega _{p}$ plasmafrekvensen . Interaktionsenergin är därför

$$E=-{\frac {1}{2}}{\frac {a_{1}a_{2}}{4\pi r}}{\vec {v}}_{1}\cdot \ vänster[1+{\hat {r}}{\hat {r}}\right]\cdot {\vec {v}}_{2}\;e^{-\omega _{p}r}\left \{{\frac {2}{\left(\omega _{p}r\right)^{2}}}\left(e^{\omega _{p}r}-1\right)-{\ frac {2}{\omega _{p}r}}\right\}.$$

Magnetisk interaktion mellan strömslingor i en enkel plasma eller elektrongas

Interaktionsenergin

Betrakta ett rör med ström som roterar i ett magnetfält inbäddat i en enkel plasma eller elektrongas. Strömmen, som ligger i planet vinkelrätt mot magnetfältet, definieras som

$${\vec {J}}_{1}({ \vec {x}})=a_{1}v_{1}{\frac {1}{2\pi rL_{B}}}\;\delta ^{2}{\left(r-r_{B1} \right)}\left({\hat {b}}\times {\hat {r}}\right)$$

var

$$r_{B1}={\frac {{\sqrt {4\pi }}m_{1}v_{1}}{a_{1}B} }$$

och ${\hat {b}}$ är enhetsvektorn i magnetfältets riktning. Här anger $L_{B}$ materialets dimension i magnetfältets riktning. Den tvärgående strömmen, vinkelrät mot vågvektorn , driver den tvärgående vågen .

Interaktionens energi är

$$E=\left({\frac {a_{1}\,a_{2}}{2\pi L_{B}}}\right)v_{1}\,v_{2}\ ,\int _{0}^{\infty }{k\;dk\;}D\left(k\right)\mid _{k_{0}=k_{B}=0}{\mathcal {J} }_{1}{\left(kr_{B1}\right)}{\mathcal {J}}_{1}{\left(kr_{B2}\right)}{\mathcal {J}}_{0 }{\left(kr_{12}\right)}$$

där $r_{12}$ är avståndet mellan mitten av de nuvarande slingorna och ${\mathcal {J}}_{n}(x)$ är en Bessel-funktion av den första sorten. För att erhålla interaktionsenergin använde vi oss av integralerna

$$\int _{0}^{2\pi }{\frac {d\varphi }{2\pi }}\exp \left(ip\cos \left(\varphi \right)\right)={\mathcal {J}}_{0}\left(p\right)$$

och

$$\int _{0}^{2\pi }{\frac {d\varphi }{2\pi }}\cos \left(\varphi \right)\exp \left(ip\cos \left( \varphi \right)\right)=i{\mathcal {J}}_{1}\left(p\right).$$

Se Vanliga integraler i kvantfältteori § Vinkelintegration i cylindriska koordinater .

En ström i ett plasma begränsat till planet vinkelrätt mot magnetfältet genererar en extraordinär våg . Denna våg genererar Hall-strömmar som interagerar och modifierar det elektromagnetiska fältet. Spridningsförhållandet för extraordinära vågor är

$$-k_{0}^{2}+{\vec {k}}^{2}+ \omega _{p}^{2}{\frac {k_{0}^{2}-\omega _{p}^{2}}{k_{0}^{2}-\omega _{H} ^{2}}}=0,$$

som ger för propagatorn

$$D\left(k\right)\mid _{k_{0}=k_{B}=0}\ ;=\;-\left({\frac {1}{{\vec {k}}^{2}+k_{X}^{2}}}\höger)$$

var

$$k_{X}\equiv {\frac {\omega _{p}^{2}}{\omega _{H}}}$$

i analogi med Darwin-propagatorn. Här ges den övre hybridfrekvensen av

$$\omega _{H}^{2}=\omega _{p}^{2}+\omega _{c}^{2},$$

cyklotronfrekvensen ges av ( Gaussiska enheter )

$$\omega _{c}={\frac {eB}{mc}},$$

och plasmafrekvensen ( gaussiska enheter )

$$\omega _{p}^{2}={\frac {4\pi ne^{2}}{m}}.$$

Här är n elektrontätheten, e är storleken på elektronladdningen och m är elektronmassan.

Interaktionsenergin blir, för som strömmar,

$$E=-\left({\ frac {a^{2}}{2\pi L_{B}}}\right)v^{2}\,\int _{0}^{\infty }{\frac {k\;dk}{{ \vec {k}}^{2}+k_{X}^{2}}}{\mathcal {J}}_{1}^{2}\left(kr_{B}\right){\mathcal { J}}_{0}\left(kr_{12}\right)$$

Gräns ​​för litet avstånd mellan strömslingor

I gränsen att avståndet mellan strömslingor är litet,

$$E=-E_{0}\;I_{1}\left(\mu \right)K_{1}\left(\mu \right)$$

var

$$E_{0}=\left({\frac {a^{2}}{2\pi L_{B}}}\right)v^{2 }$$

och

$$\mu ={\frac {\omega _{p}^{2}r_{B}}{\omega _{H}}}=k_ {X}\;r_{B}$$

och I och K är modifierade Bessel-funktioner. vi har antagit att de två strömmarna har samma laddning och hastighet.

Vi har använt integralen (se Vanliga integraler i kvantfältteori § Integration av den cylindriska propagatorn med massa )

$$\int _{o}^{\infty }{\frac {k\;dk}{k^{2}+m^{2}}}{\mathcal {J}}_{1}^{ 2}\left(kr\right)=I_{1}\left(mr\right)K_{1}\left(mr\right).$$

För liten mr blir integralen

$$I_{1}\left(mr\right)K_{1}\left(mr\right)\rightarrow {\frac {1}{2}}\left[1-{\frac {1}{8 }}\left(mr\right)^{2}\right].$$

För stor mr blir integralen

$$I_{1}\left(mr\right)K_{1}\left(mr\right)\rightarrow {\frac {1}{2}}\;\left({\frac {1}{mr }}\höger).$$

Relation till kvanthalleffekten

Screeningsvågnumret kan skrivas ( gaussiska enheter )

$$\mu ={\frac {\omega _{p}^{2}r_{B}}{\omega _{H}c}}=\left({\frac {2e^{2} r_{B}}{L_{B}\hbar c}}\right){\frac {\nu }{\sqrt {1+{\frac {\omega _{p}^{2}}{\omega _ {c}^{2}}}}}=2\alpha \left({\frac {r_{B}}{L_{B}}}\right)\left({\frac {1}{\sqrt {1+{\frac {\omega _{p}^{2}}{\omega _{c}^{2}}}}}}\right)\nu$$

där $\alpha$ är finstrukturkonstanten och fyllningsfaktorn är

$$\nu ={\frac {2\pi N\hbar c}{eBA}}$$

och N är antalet elektroner i materialet och A är arean av materialet vinkelrätt mot magnetfältet. Denna parameter är viktig i kvant-Hall-effekten och fraktionerad kvant-Hall-effekt . Fyllningsfaktorn är bråkdelen av ockuperade Landau-tillstånd vid grundtillståndsenergin.

För fall av intresse för kvanthalleffekten är $\mu$ liten. I så fall är interaktionsenergin

$$E=-{\frac {E_{0}}{2}}\left[1-{\frac {1}{8}}\mu ^ {2}\right]$$

där ( Gaussiska enheter )

$$E_{0}={4\pi }{\frac {e^{2}} {L_{B}}}{\frac {v^{2}}{c^{2}}}={8\pi }{\frac {e^{2}}{L_{B}}}\vänster ({\frac {\hbar \omega _{c}}{mc^{2}}}\right)$$

är interaktionsenergin för noll fyllningsfaktor. Vi har satt den klassiska kinetiska energin till kvantenergin

$${\frac {1}{2}}mv^{2}=\hbar \omega _{c}.$$

Gravitation

En gravitationsstörning genereras av spännings-energitensorn $T^{\mu \nu }$ ; följaktligen är Lagrangian för gravitationsfältet spin -2. Om störningarna är i vila, är den enda komponenten i spännings-energitensorn som kvarstår komponenten ${\displaystyle 00} .$ Om vi ​​använder samma trick att ge gravitonen lite massa och sedan ta massan till noll i slutet av beräkningen blir propagatorn

$$D\left(k\right)\mid _{k_{0}=0}\;=\;-{\frac { 4}{3}}{\frac {1}{{\vec {k}}^{2}+m^{2}}}$$

och

$$E=-{\frac {4}{3}}{\frac {a_{1}a_{2}}{ 4\pi r}}\exp \left(-mr\right),$$

vilket återigen är attraktivt snarare än motbjudande. Koefficienterna är proportionella mot massorna av störningarna. I gränsen för liten gravitonmassa återvinner vi det omvända kvadratiska beteendet av Newtons lag.

Till skillnad från det elektrostatiska fallet ger dock inte det korrekta resultatet att ta bosonens gräns för liten massa. En mer rigorös behandling ger en faktor en i energin snarare än 4/3.