Bundet tillstånd

Inom kvantfysik är ett bundet tillstånd ett kvanttillstånd för en partikel som är föremål för en potential så att partikeln har en tendens att förbli lokaliserad i en eller flera regioner i rymden. Potentialen kan vara extern eller den kan vara resultatet av närvaron av en annan partikel; i det senare fallet kan man på motsvarande sätt definiera ett bundet tillstånd som ett tillstånd som representerar två eller flera partiklar vars interaktionsenergi överstiger den totala energin för varje separat partikel. En konsekvens är att, givet en potentiell försvinnande i oändligheten , måste negativa energitillstånd vara bundna. I allmänhet energispektrumet för uppsättningen av bundna tillstånd diskret, till skillnad från fria partiklar, som har ett kontinuerligt spektrum.

Även om de inte är bundna tillstånd i strikt mening, anses metastabila tillstånd med en netto positiv interaktionsenergi, men lång sönderfallstid, ofta också anses vara instabila bundna tillstånd och kallas "kvasibundna tillstånd". Exempel är vissa radionuklider och elektreter .

I relativistisk kvantfältteori motsvarar ett stabilt bundet tillstånd av n partiklar med massorna $\{m_{k}\}_{k=1}^{n}$ en pol i S -matrisen med en masscentrumenergi mindre än $\textstyle \sum _{k}m_{k}$ . Ett instabilt bundet tillstånd visar sig som en pol med en komplex massacentrumenergi.

Exempel

En översikt över de olika familjerna av elementära och sammansatta partiklar, och teorierna som beskriver deras interaktioner

• En proton och en elektron kan röra sig separat; när de gör det är den totala massacentrumenergin positiv, och ett sådant par av partiklar kan beskrivas som en joniserad atom. När elektronen väl börjar "kretsa" protonen blir energin negativ och ett bundet tillstånd – nämligen väteatomen – bildas . Endast det lägsta energibundna tillståndet, grundtillståndet, är stabilt. Andra exciterade tillstånd är instabila och kommer att sönderfalla till stabila (men inte andra instabila) bundna tillstånd med mindre energi genom att sända ut en foton .
• En positronium "atom" är ett instabilt bundet tillstånd av en elektron och en positron . Det sönderfaller till fotoner .
• Varje tillstånd i den kvantharmoniska oscillatorn är bundet, men har positiv energi. Observera att ${\displaystyle \lim _{x\to \pm \infty }{V_{\text{QHO}}(x)}=\infty } ,$ så nedan gäller inte.
• En kärna är ett bundet tillstånd av protoner och neutroner ( nukleoner ).
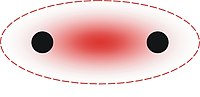
• Protonen i sig är ett bundet tillstånd av tre kvarkar (två upp och en ner ; en röd , en grön och en blå ). Men till skillnad från fallet med väteatomen kan de enskilda kvarkarna aldrig isoleras. Se fängelse .
• Modellerna Hubbard och Jaynes–Cummings–Hubbard (JCH) stöder liknande bundna tillstånd. I Hubbard-modellen kan två repulsiva bosoniska atomer bilda ett bundet par i ett optiskt gitter . JCH Hamiltonian stöder också tvåpolaritonbundna tillstånd när foton-atominteraktionen är tillräckligt stark.

Definition

Låt H vara ett komplext separerbart Hilbertrum, $U=\lbrace U(t)\mid t\in \mathbb {R} \rbrace$ vara en enparameter grupp av enhetsoperatorer på H och $\rho =\rho (t_{0})$ vara en statistisk operator på H . Låt A vara en observerbar på H och $\mu (A,\rho )$ vara den inducerade sannolikhetsfördelningen av A med avseende på ρ på Borel σ-algebra för $\mathbb {R}$ . Då är utvecklingen av ρ inducerad av U bunden med avseende på A om ${\displaystyle \lim _{R\rightarrow \infty }{\sup _{t\geq t_{0}}{\mu (A,\rho (t))(\mathbb {R} _{>R})}}=0} ,$ där $\mathbb {R} _{>R}=\lbrace x\in \mathbb {R} \mid x>R\rbrace$ .

Mer informellt finns ett bundet tillstånd inom en begränsad del av spektrumet av A . För ett konkret exempel: låt $H=L^{2}(\mathbb {R} )$ och låt A vara position. Givet kompakt stöd $\rho =\rho (0)\in H$ och $[-1,1] \subseteq \mathrm {Supp} (\rho )$ .

• Om tillståndsutvecklingen av ρ "flyttar detta vågpaket konstant åt höger", t.ex. om $[t-1,t+1 ]\in \mathrm {Supp} (\rho (t))$ för alla $t\geq 0$ , då är ρ inte bundet tillstånd med avseende på position.
• Om $\rho$ inte ändras med tiden, dvs $\rho (t)=\rho$ för alla $t\geq 0$ , då ${\ displaystyle \rho }$ är bunden med avseende på position.
• Mer allmänt: Om tillståndsutvecklingen för ρ "bara flyttar ρ inuti en avgränsad domän", så är ρ bunden med avseende på position.

Egenskaper

Låt A ha mått-space-kodomän $(X;\mu )$ . En kvantpartikel är i ett bundet tillstånd om den aldrig hittas "för långt bort från någon ändlig region $R\subseteq X$ ", dvs med hjälp av en vågfunktionsrepresentation,

$${\begin{aligned}0&=\lim _{R\to \infty }{\mathbb {P} ({\text{partikel uppmätt inuti }}X\setminus R)}\ \&=\lim _{R\to \infty }{\int _{X\setminus R}|\psi (x)|^{2}\,d\mu (x)}\end{aligned}}$$

Följaktligen, ${\textstil \int _{X}{|\psi (x)|^{2}\,d\mu (x)}}$ är ändlig. Med andra ord är ett tillstånd ett bundet tillstånd om och endast om det är ändligt normaliserbart.

Eftersom ändligt normaliserbara tillstånd måste ligga inom den diskreta delen av spektrumet, måste bundna tillstånd ligga inom den diskreta delen. Men, som Neumann och Wigner påpekade, kan ett bundet tillstånd ha sin energi placerad i kontinuumspektrat. I så fall är bundna tillstånd fortfarande en del av den diskreta delen av spektrumet, men visas som Dirac-massor i det spektrala måttet.

Positionsbundna tillstånd

Betrakta en-partikel Schrödinger-ekvationen. Om ett tillstånd har energi ${\textstil E<\max {\left(\lim _{x\to \infty }{ V(x)},\lim _{x\to -\infty }{V(x)}\right)}},$ då uppfyller vågfunktionen ψ , för vissa $X>0$

${\frac {\psi ^{\prime \prime }}{\psi }}={\frac {2m }{\hbar ^{2}}}(V(x)-E)>0{\text{ för }}x>X$

så att ψ undertrycks exponentiellt vid stora x . Därför är negativa energitillstånd bundna om V försvinner i oändligheten.

Krav

En boson med massa m _χ som förmedlar en svagt kopplad interaktion producerar en Yukawa-liknande interaktionspotential,

$V(r)=\pm {\frac {\alpha _{\chi }}{r}}e^{-{\frac {r} {\lambda \!\!\!{\frac {}{\ }}_{\chi }}}}$ ,

där ${\displaystyle \alpha _{\chi }=g^{2}/4\pi } ,$ g är mätarens kopplingskonstant och ƛ _i = ℏ / m _i c är den reducerade Compton våglängd . En skalär boson producerar en universellt attraktiv potential, medan en vektor attraherar partiklar till antipartiklar men stöter bort som par. För två partiklar med massan m ₁ och m ₂ blir systemets Bohr- radie

$a_{0}={\frac {{\lambda \!\!\!^{{}^{\underline {\ \ }}}}_{1 }+{\lambda \!\!\!^{{}^{\underline {\ \ }}}}_{2}}{\alpha _{\chi }}}$

och ger det dimensionslösa talet

$D={\frac {{\lambda \!\!\!^{{ }^{\underline {\ \ }}}}_{\chi }}{a_{0}}}=\alpha _{\chi }{\frac {{\lambda \!\!\!^{{} ^{\underline {\ \ }}}}_{\chi }}{{\lambda \!\!\!^{{}^{\underline {\ \ }}}}_{1}+{\lambda \!\!\!^{{}^{\underline {\ \ }}}}_{2}}}=\alpha _{\chi }{\frac {m_{1}+m_{2}}{ m_{\chi }}}$ .

För att det första bundna tillståndet alls ska existera är $D\gtrsim 0,8$ . Eftersom fotonen är masslös är D oändlig för elektromagnetism . För den svaga interaktionen är Z -bosonens massa 91,1876 ± 0,0021 GeV/ c ² , vilket förhindrar bildandet av bundna tillstånd mellan de flesta partiklar, eftersom den är 97,2 gånger protonens massa och 178 000 gånger elektronens massa.

Observera dock att om Higgs-interaktionen inte bröt den elektrosvaga symmetrin på den elektrosvaga skalan , så skulle den svaga SU(2) -interaktionen bli begränsande .

Se även

• Sammansatt fält
• Resonans (partikelfysik)
• Bethe–Salpeters ekvation
• Cooper par

Vidare läsning

•   Blanchard, Philippe; Brüning, Edward (2015). "Några tillämpningar av den spektrala representationen". Mathematical Methods in Physics: Distributions, Hilbert Space Operators, Variational Methods, and Applications in Quantum Physics ( 2nd ed.). Schweiz: Springer International Publishing. sid. 431. ISBN 978-3-319-14044-5 .

•   Gustafson, Stephen J.; Sigal, Israel Michael (2011). "Spektrum och dynamik". Mathematical Concepts of Quantum Mechanics (2nd ed.). Berlin, Heidelberg: Springer-Verlag. sid. 50. ISBN 978-3-642-21865-1 .

•   Ruelle, David (9 januari 2016). "En anmärkning om bundna tillstånd i teori om potentiell spridning" (PDF) . Nuovo Cimento A . 61 (juni 1969): 655–662. doi : 10.1007/BF02819607 . S2CID 56050354 . Hämtad 27 december 2021 .