Regel för marteloio

Tondo e quadro (cirkel och fyrkant) från Andrea Biancos atlas från 1436

Regeln för marteloio är en medeltida teknik för navigationsberäkning som använder kompassriktning , avstånd och en enkel trigonometrisk tabell känd som toleta de marteloio . Regeln berättade för sjömän hur man ritar traversen mellan två olika navigationskurser genom att lösa trianglar med hjälp av Toleta och grundläggande aritmetik .

De som är obekväma med att manipulera siffror kan ta till den visuella tondo e quadro (cirkel-och-kvadrat) och uppnå sitt svar med avdelare . Regeln för marteloio användes vanligen av Medelhavsnavigatörer under 1300- och 1400-talen, innan utvecklingen av astronomisk navigering .

Etymologi

Etymologin kommer från det venetianska språket . I sin atlas från 1436 introducerade den venetianske kaptenen och kartografen Andrea Bianco en siffertabell som han kallade toleta de marteloio ("marteloios tabell"), och metoden att använda den som raxon de marteloio ("reason of marteloio").

Innebörden av marteloio i sig är osäker. Den mest allmänt accepterade hypotesen, som först skickades fram av AE Nordenskiöld , är att marteloio relaterar till " hammare " ("martelo" på venetianska), och syftar på den lilla hammaren som användes för att slå i fartygsklockan ombord för att markera tidens gång . Det har föreslagits att suffixet - oio antyder att marteloio inte helt betydde själva hammaren eller hammaren, utan snarare "hamringen", med avsikt att indikera "hamringen, ljudet, racketen" från klockans byte var fjärde timmar. Eftersom det fanns många visare på däck under ett vaktbyte skulle det vara ett lägligt tillfälle för fartygets lots att beordra en ändring av bäringen (om nödvändigt).

Alternativa hypoteser (inte tillnärmelsevis lika accepterade) är att "marteloio" är en förvanskning av mari logio (som betyder "havsstyre"), eller från mare tela (som betyder "havsnätverk"), eller att det härstammar från det grekiska homartologium ( όμαρτόλογίον , som betyder "sällskapsstycke"), eller från grekiskan imeralogium ( ήμερόλογίον , som betyder "daglig beräkning") eller att det kan vara från den nordfranska matelot , som i sin tur kommer från Brenning martoaillod (meton.

Syfte

1400-talssjöman konsulterar en kompass ombord på fartyget (från John Mandeville 's Travels , 1403)

"Rule of marteloio" användes i europeisk sjöfart på medeltiden, mest notably i Medelhavet mellan 1300- och 1500-talen, även om den kan ha äldre rötter. Det var en integrerad del av navigering med "kompass och sjökort", innan tillkomsten av geografiska koordinater och utvecklingen av himmelsnavigering i Europa.

Medeltida navigering förlitade sig på två parametrar, riktning och avstånd. Ombord på fartyget bestämdes riktningen av sjömannens kompass (som dök upp omkring 1300). Avstånd mättes med dödräkning , ( dvs. avstånd = hastighet × tid), där tiden mättes med ett halvtimmesglas och hastighetsavläsningar togs med någon form av en spånlogg (den arkaiska metoden, som används i 1300- och 1400-talen, involverade att häva en bit trä eller flytgods överbord; besättningen engagerade sig i en rytmisk sång för att markera den tid det tog för chipet att flyta förbi fartygets längd).

Anonymt genuesiskt portolandiagram från ca. 1325 till ca. 1350. ( Library of Congress , Washington DC)

Att rita en kurs krävde att man kunde kompassriktningen och avståndet mellan punkt A och punkt B. Kunskap om var hamnarna låg i förhållande till varandra förvärvades av navigatörer genom lång erfarenhet till sjöss. Denna information samlades ibland och skrevs ner i en pilothandbok, känd som en portolano ("hamnbok", på italienska, motsvarande grekiska periplus , portugisiska roteiro och engelska rutter ). Dessa handböcker användes för att konstruera en klass av nautiska kartor som kallas portolan sjökort . Portolan-diagram började produceras i Genua i slutet av 1200-talet och spred sig snart till Venedig och Mallorca . Portolan-sjökort var inte rutnät av longitud- och latitudlinjer, utan snarare av ett nät av kompassrumblinjer , vilket gav sjöfararna en uppfattning om endast avståndet och riktningen mellan platserna.

32-vinds kompassros med traditionella namn (och traditionell färgkod).

Genom en handbok eller ett portolan-kort kunde en navigatör omedelbart se att till exempel Pisa låg 85 miles sydost ("Scirocco" i den traditionella kompassrosnomenklaturen ) i Genua , och så skulle ett fartyg som gav sig ut från Genua till Pisa helt enkelt behålla den bäringen för det avståndet. De flesta seglingskurser var dock inte alls så snygga. En sjöman som ville segla från Mallorca till Neapel kunde säga att den senare var rakt österut ("Levante") cirka 600 miles - men ön Sardinien ligger i vägen, därför måste fartygets bäring ändras längs rutten. Detta är lättare sagt än gjort, eftersom geografiska koordinater inte fanns under den här eran. Det enda sättet att bestämma den exakta positionen för fartyget till havs skulle vara att beräkna via tidigare bäring och tillryggalagd sträcka.

Öar var ett förutsägbart hinder – att kringgå Sardinien skulle helt enkelt vara en fråga om att segla sydost en viss sträcka och sedan ändra bäringen till nordost ("Greco") för resten. Mer problematiskt är om fartyget blåstes av sin avsedda rutt av hårda vindar, eller var tvungen att ägna sig åt att slå , ändra bäring upprepade gånger. Hur återgår den till sin avsedda kurs? Det var här regeln om marteloio kom in.

Traversproblemet

Regeln om marteloio tog upp problemet med att ändra bäring till sjöss. Närmare bestämt hjälpte det en navigator att rita traversen från en navigationskurs till en annan. Anta till exempel att ett fartyg skulle segla från Korsika till Genua , en kurs som bär rakt norrut ("Tramontana") i cirka 130 miles. Men vindarna samarbetar inte, och fartyget tvingades segla nordväst ("Maestro") i cirka 70 miles. Hur återgår den till sin ursprungliga rutt? Att återställa sin bäring mot nordost ("Greco") verkar klokt nog, men hur länge ska den segla på den bäringen? Hur skulle en navigatör veta när fartyget hade nått sin gamla rutt och borde svänga norrut igen? Hur undviker man att överskrida eller underskrida den gamla banan?

Traversproblemet: avsedd kurs AB (lager N), faktisk kurs AC (lager NV). Att beräkna ritorno (avstånd på returkurs CD , bäring NE) och avanzo (avstånd som är bra på avsedd kurs) är en fråga om att lösa triangeln ACD

Detta är ett matematiskt problem för att lösa en triangel . Om en navigatör vet hur länge fartyget har seglat på den felaktiga kursen, kan han beräkna dess aktuella avstånd från dess avsedda kurs, och uppskatta hur länge det måste segla tillbaka på en ny bäring tills det återställer sin gamla kurs. I exemplet från Korsika till Genua finns det en implicit triangel ACD , med en sida given ( AC = 70 miles på faktisk NV kurs), en 45° vinkel vid A (skillnadsvinkel mellan faktisk kurs NV och avsedd kurs N) och ytterligare en vinkel på 90° vid C (skillnadsvinkel mellan faktisk kurs NV och returkurs NE). Utmaningen för navigatören är att ta reda på hur länge man måste segla på NE returkurs (längden på sido- CD , det som kallas ritorno ) och hur långt man har avancerat på den avsedda kursen när man rätar ut (längden) av hypotenusan AD , eller det som kallas total avanzo ).

Detta är elementär trigonometri , som löser två sidor med en sida (70) och två vinklar (45° och 90°). Detta görs snabbt genom att tillämpa sinuslagen :

ger upp lösningarna ritorno = 70 miles och total avanzo = 98,99 miles. Detta innebär att om fartyget bär NE från sin nuvarande position ( C ), kommer det att nå sin ursprungliga avsedda kurs efter 70 mils segling på NE-bäringen. När den når sin korsningspunkt ( D ) kommer den att ha tillryggalagt 98,99 miles av sin ursprungliga avsedda kurs. Där kan den räta ut sin bäring N och segla de återstående 30 milen eller så till Genua.

Tyvärr kunde medeltida sjömän med de rudimentära utbildningsnivåerna från 1300- och 1400-talen inte känna till sinuslagen eller manipulera den med lätthet. Som ett resultat behövde medeltida navigatörer en enklare och mer tillgänglig beräkningsmetod.

Regler

Ramon Llulls "miliaria"

Den lärde prästen Ramon Llull från Mallorca var den första författare som hänvisade till en regel för att lösa traversproblemet med navigering. I sin Arbor Scientiae (1295), i avsnittet med frågor om geometri, skriver Llul:

Hur mäter sjömän miles till havs ( miliaria in mari ) ? Sjöfarare betraktar de fyra allmänna vindarna, det vill säga den östra, västra, norra och södra, och även ytterligare fyra vindar som ligger mellan dem, grec (NO), exaloch (SE), lebeg (SW) och maestre (NW). Och de tittar noggrant på mitten av cirkeln där vindarna (rumberna) möts i vinklar; de överväger när ett fartyg färdas med ostvinden ( levant ) 100 miles från centrum, hur många miles det skulle göra på den sydostliga ( exaloch ) vinden; och för 200 miles fördubblar de antalet genom att multiplicera och sedan vet de hur många miles det är från slutet av varje 100 miles i östlig riktning till motsvarande punkt i sydostlig riktning. Och för detta har de det här instrumentet [en matematisk tabell?] och ett diagram, rutter, nål och polstjärnan."

Vad Llull verkar försöka förklara är att ett fartyg som faktiskt seglar E, men som har för avsikt att segla SE, kan ta reda på hur mycket av sin avsedda sydostliga sträcka det redan har gjort bra – vad italienarna kallade "avanzar", men Lull verkar att kalla " miliaria in mari ". Llull förklarar inte exakt hur, utan hänvisar bara till ett "instrument", förmodligen någon sorts trigonometrisk tabell. Lull antyder att sjöfarare kan beräkna miliaria på den avsedda kursen genom att multiplicera den sträcka som faktiskt seglats på den felaktiga kursen med cosinus för vinkeln mellan de två rutterna.

Ramon Lulls miliaria in mari , från hans exempel från 1295.
Miliaria in mari = seglat avstånd × cos( θ )

där θ är skillnadsvinkeln mellan de två vägarna.

Om man använder Lulls exempel, ett fartyg som hade för avsikt att segla sydost ("Exaloch" är katalanska för "Scirocco") men som istället tvingades segla österut ("Levant"), så är skillnadsvinkeln θ = 45°. Efter 100 miles på den felaktiga rutten miliaria på den avsedda rutten 100 × cos 45° = 70,71. Fördubbling av seglingen på den felaktiga rutten till 200 miles kommer att fördubbla miliaria på den avsedda rutten till 141,42 miles (= 200 cos 45°).

mäts Lulls miliaria in mari genom att konstruera en rätvinklig triangel genom att dra en lina från den sträcka som seglats på den faktiska banan till den avsedda banan och möta den senare i en 90° vinkel).

Llull är lite mer explicit i sin Ars magna generalis et ultima (skriven ca 1305). Omvända sitt exempel, med ett fartyg som faktiskt seglar sydost men avser att segla österut, Llull noterar att för varje fyra mil på den sydöstra bäringen "vinner det tre miles" (2,83 faktiskt) på den avsedda österut. Således, konstaterar Lull, "förlorar fartyget 25 miles" (29 faktiskt) av sin avsedda kurs för varje 100 miles det seglar på den nuvarande kursen.

Lägg märke till att Ramon Lull i sina passager inte rekommenderar regeln, utan rapporterar den, och insinuerar att denna regel redan var känd och användes av samtida sjömän i praktiken. Detta är kanske inte förvånande – även om trigonometri bara var i sin linda i det kristna Europa, var sinus- och cosinustabeller redan kända i arabisk matematik . Konungariket Mallorca , under muslimskt styre fram till 1230-talet, förblev ett mångkulturellt centrum på Lulls tid, med blomstrande judiska samhällen , av vilka många sysslade med matematik och astronomi, och vars sjöfarare hade omfattande kontakter över Medelhavet. Att mallorcanska navigatörer hade någon sorts trigonometrisk tabell till hands är inte osannolikt. Icke desto mindre är det exakta innehållet och layouten av denna tabell som antyddes av Ramon Llull 1295 osäker.

Andrea Biancos "toleta"

Toleta de marteloio från Andrea Biancos atlas från 1436

Vi får vår första glimt av en sjömans trigonometriska bord mer än ett sekel efter Llull. I den första folion i sin portolanatlas från 1436 förklarar den venetianske kaptenen Andrea Bianco raxon de marteloio , hur man beräknar traversen och återställer kursen. Han lägger upp en enkel trigonometrisk tabell som han kallar toleta de marteloio och rekommenderar att sjöfarare lägger bordet i minnet.

Toleta de marteloio är utformad enligt följande:


Kvartal (avvikelsevinkel)
Alargar (Avstånd från kurs)
Avanzar (Advance on true course)
Kvartal (returvinkel)
Ritorno (Återgå till kursen)
Avanzo di ritorno (Förskott under returen)
1 20 98 1 51 50
2 38 92 2 26 24
3 55 83 3 18 15
4 71 71 4 14 10
5 83 55 5 12 6 1⁄2 _ _
6 92 38 6 11 4
7 98 20 7 10 1⁄5 _ _ 2 1⁄5 _ _
8 100 0 8 10 0
För varje 100 mil För varje 10 mil alargar

Siffrorna i Toleta kan approximeras med de moderna formlerna:

  • Alargar = 100 × sin ( q × 11,15)
  • Avanzar = 100 × cos ( q × 11,15)
  • Ritorno = 10 / sin ( q × 11,15)
  • Avanzo di ritorno = 10 / brun ( q × 11,15)

där q = antal kvartsvindar (skillnadsvinkel uttryckt i antal kvartsvindar). (märk på att siffrorna fungerar med kvartsvindar inställda på 11,15° intervall, snarare än 11,25°, den vanliga definitionen av en kvartsvind).

Toleta är en enkel tabell med flera kolumner med siffror . I den första kolumnen visas skillnadsvinkeln mellan faktiska och avsedda banor, uttryckt som antal kvartsvindar . När den skillnaden har bestämts ger den andra kolumnen Alargar ("Utvidgningen", det aktuella avståndet som fartyget är från den avsedda kursen) medan den tredje kolumnen talar om för Avanzar ("Förskottet", hur mycket av avståndet på den avsedda kursen kursen har redan täckts av segling på nuvarande bäring – detta motsvarar Ramon Llulls miliaria di mari ). Alargar- och Avanzar-siffrorna visas på Biancos tabell för 100 mils segling på den aktuella banan.

Beräknar alargar och avanzar från Biancos Toleta .

Exempel : anta att ett fartyg hade för avsikt att segla österut ("Levante") från punkt A till punkt B. Men anta att vindarna tvingade det att segla på en sydost-vid-östlig kurs (SEbE, "Quarto di Scirocco verso Levante"). Sydost-vid-öst är tre fjärdedels vindar (eller 33,75°) från öst (på en 32-punkts kompass , i ordning efter kvartsvindar bort från öst, 1 fjärdedel är öst-vid-syd, 2 fjärdedelar är öst-sydost , 3 fjärdedelar är sydost-vid-öst). Det betyder att navigatorn bör konsultera den tredje raden, q = 3, på toletan.

Anta att fartyget seglade 100 miles på SE-by-E-lagret. För att kontrollera sitt avstånd från den avsedda kursen österut kommer sjöfararen att läsa motsvarande post på alargarkolumnen och omedelbart se att han är 55 mil bort från den avsedda kursen. Avanzarkolumnen informerar honom om att efter att ha seglat 100 miles på den nuvarande SEbE-banan har han tillryggalagt 83 miles av den avsedda E-banan .

Nästa steg är att bestämma hur man ska återgå till den avsedda kursen. För att fortsätta exemplet, för att komma tillbaka till den avsedda kursen österut, måste vår sjöman omorientera fartygets bäring i nordostlig riktning. Men det finns olika nordostliga vinklar – NbE, NNE, NE, ENE, etc. Sjöfararen har ett val av bäring – om han återvänder med en skarp vinkel (t.ex. norr med öst), kommer han att återgå till den avsedda kursen snabbare än vid en mildare gradient (t.ex. öst mot norr). Vilken vinkel han än väljer, måste han härleda exakt hur länge han måste segla på den bäringen för att nå sin gamla kurs. Om han seglar för länge riskerar han att överskjuta den.

Beräknar ritorno och avanzo di ritorno

Att beräkna returkursen är vad de tre sista kolumnerna i toletan är till för. I den fjärde kolumnen uttrycks returvinklarna som fjärdedelar från den avsedda kursbäringen ( inte aktuell kursbäring). I vårt exempel tänkte sjöfararen gå österut, men har seglat sydost för öst i 100 miles. Med tanke på vindarna bestämmer han sig för att det är bäst att återvända till den ursprungliga kursen genom att omorientera fartyget öst-nordost (ENE, "Greco-Levante"). ENE är två kvartsvindar över den avsedda bäringen, öster, så nu tittar han på andra raden ("kvarts = 2") på den fjärde kolumnen i tabellen.

Den femte kolumnen är ritorno , sträckan han måste färdas på den valda returvinkeln för att återhämta den ursprungliga kursen. Med tanke på att han har valt att återvända med ENE-bäring (q = 2), måste han läsa den andra raden i ritorno- kolumnen , som visar siffran 26. Detta representerar det erforderliga antalet miles som han måste färdas på ENE-bäring för varje 10 miles han avvek. Kom ihåg att hans alargar (avstånd från avsedd kurs) var 55 miles. Så för att återgå till sin avsedda kurs måste han resa 5,5 × 26 = 143 miles på ENE. Med andra ord behöver han hålla sin ENE-riktning i 143 miles; när den sträckan väl är tillryggalagd bör han räta upp sitt skepp österut, och han kommer att vara exakt tillbaka på den avsedda kursen.

Den sjätte och sista kolumnen ( avanzo di ritorno ) anger längden på den avsedda banan som han har gjort gott av sin hemresa. Detta uttrycks också i termer per 10 miles alargar. Hans alargar var 55, och hans returvinkel var ENE (därmed q = 2), det betyder att hans avanzo di ritorno är 5,5 × 24 = 132. Med andra ord, om allt går rätt, och vår sjöman håller sin ENE-riktning i 143 miles ( ritorno ), sedan kommer han under den återkomsten att ha tillryggalagt ytterligare 132 miles på sin avsedda kurs österut ( avanzo di ritorno ) .

Slutligen, för att beräkna det totala avståndet bra (totalt avanzo) på den österutgående bäringen av hela hans äventyr, måste han lägga till avanzaren under avvikelsen (83 miles) plus avanzo di ritorno (132 miles). På det hela taget har han alltså tillryggalagt 83 + 132 = 215 mil på den tänkta banan. Genom att mäta det avståndet på kartan från startpunkten ( A ), kan sjöfararen ta reda på sin exakta nuvarande position.

Detta är den enklaste användningen av toleta de marteloio. Det är vid roten en trigonometrisk tabell. Den tar dock inte tag i traversproblemet på en gång, som sinuslagen, utan delar upp problemet i två rätvinkliga trianglar som den fortsätter att lösa successivt. Modern trigonometri skulle avstå från steget att beräkna alargar och beräkna ritorno direkt - men för det måste man vara beväpnad med en full sinustabell . Toletan är en ganska enkel tabell, lätt att konsultera och utföra beräkningar med, och tillräckligt kompakt för att kunna memoreras av navigatörer (som Bianco rekommenderar).

Reguladetri

Toleta de marteloio uttrycks för fina runda tal, 100 och 10. Men i praktiken skulle ett fartyg vanligtvis inte segla 100 miles innan det försöker återvända, utan någon annan sträcka, säg 65 miles. För att beräkna detta är ett enkelt problem att lösa kvoter . Till exempel, om fartyget hade seglat 65 miles på sydost-vid-öst, då är att beräkna alargaret från den avsedda kursen österut helt enkelt en fråga om att lösa följande för x :

där 55 är alargar för 100 miles (som ges i den andra kolumnen i tabellen vid q = 3). Detta görs enkelt med den enkla " regeln om tre ", en metod för korsmultiplikation, som använder tre tal för att lösa det fjärde genom successiv multiplikation och division:

x = 65 × 55 ÷ 100

Så att segla 65 miles på SE by E innebär alargar = x = 35,75 miles. Avanzar, etc. kan räknas ut analogt.

Medan "regeln om tre" var känd redan på 1300-talet, kunde skicklighet i att utföra multiplikation och division vara svårfångad för medeltida sjömän hämtade från det som till stor del var ett analfabetsamhälle. Ändå var den inte otillgänglig. Som Andrea Bianco uppmanade, bör navigatörer "veta hur man multiplicerar väl och dividerar väl" ("saver ben moltiplichar e ben partir") Det är här vi ser det viktiga gränssnittet mellan handel och navigering . Handelns matematik – arabiska siffror , multiplikation, division, bråk , verktygen som behövs för att beräkna köp och försäljning av varor och andra kommersiella transaktioner – var i huvudsak densamma som navigationsmatematiken. Och denna typ av matematik lärdes ut vid kulramsskolorna som grundades på 1200-talet i de kommersiella centra i norra Italien för att utbilda söner till köpmän, samma klass som italienska navigatörer hämtades ifrån. Som historikern EGR Taylor noterar, "sjömän var den första yrkesgruppen som använde matematik i sitt dagliga arbete"

Cirkel och fyrkant

Återgivning av grunddragen i tondo e quadro

För dem som besväras av den höga konsten att manipulera siffror fanns det ett alternativ. Detta var den visuella enheten känd som "cirkeln och kvadraten" ( tondo e quadro ), som också tillhandahålls av Andrea Bianco i hans atlas från 1436.

Cirkeln var en 32-vinds kompassros (eller samling av rhumb-linjer). Cirkeln var inskriven med ett 8 × 8 kvadratiskt rutnät.

Kompassrosen i mitten kan förbises – ja, själva cirkeln kan ignoreras, eftersom den inte verkar ha något annat syfte än konstruktionen av strålarna som löper över nätet. Rosen av intresse finns i det övre vänstra hörnet av det kvadratiska rutnätet. Från det hörnet utgår en serie kompasslinjer . I sin ursprungliga tondo e quadro från 1436 har Bianco sexton emanerande strålar – det vill säga Bianco inkluderar halvkvartsvindar, eller åttondevindar ( otava ), så att de emanerande strålarna har intervaller på 5,625 grader. Andra konstruktioner av cirkeln och kvadraten, t.ex. Cornaro Atlas , använder endast åtta strålar som emanerar vid kvartsvindsavstånd (11,25 grader). Visuellt replikerar dessa strålar den nedre högra fjärdedelen av en kompassros med 32 vindar: öster (0q), E med S (1q), ESE (2q), SE med E (3q), SE (4q), SE med S ( 5q), SSE (6q), S by E (7q) och South (8q).

Reproduktion av taktskalan av Biancos tondo e quadro

Ovanför rutnätet finns en skala för avståndsstreck , skårad med underenheter. Det finns två uppsättningar siffror på skalan, en för att mäta varje rutnätsruta med 20 miles, en annan för att mäta varje rutruta med 100 miles (se diagram). Det översta fältet är 20m-per-kvadratskalan, där varje svart prick anger en mil. Den nedre stapeln är 100m-per-kvadratskalan, där längden på en enhetskvadrat är uppdelad i två lika stora 50m-delrutor, och en uppsättning punkter och röda linjer bryter ner den ytterligare i längder på 10 miles. Så beroende på vilken skala man väljer kan längden på sidan av hela rutnätet (åtta rutor) mätas upp till 160 miles (med skalan 20 m per kvadrat) eller upp till 800 miles (med 100 m-per) -kvadratskala).

Detalj av Biancos tondo e quadro

Keruben med avdelare föreslår hur en navigator är tänkt att använda rutnätet för att beräkna alargar och avanzar genom visuell mätning snarare än att manipulera siffror.

Lösa en triangel med tondo e quadro

Exempel : anta att fartyget har färdats 120 miles vid två kvartsvindar under den avsedda kursen (t.ex. rest på ESE, när den avsedda kursen är österut). Med hjälp av avdelare och 20m-skalan kan navigatören mäta ut 120 miles med sina avdelare. Sedan sätter han ena änden i det övre vänstra hörnet ( A ), lägger han ut avdelare längs ESE-strålen (= två kvartsvindar under öststrålen, eller horisontell toppen av rutnätet) och markerar platsen (punkt B på diagrammet ). Använd sedan en linjal för att dra en linje upp till den östliga strålen och markera motsvarande fläck C .

Det är lätt att direkt se att en rätvinklig triangel ABC har skapats. Längden BC är alargar (avstånd från avsedd kurs), som kan mätas som 46 miles (detta kan visuellt ses som två rutnätsrutor plus en bit, det vill säga 20m + 20m och en liten bit som kan bedömas som 6m av med hjälp av avdelare och 20 m barskalan). Längden AC är avanzar (avstånd gjort bra), vilket är 111 miles – visuellt, fem rutnätsrutor och en bit, eller (20 × 5) + 11, mätt med avdelare och skala igen.

Detta är hur "cirkeln och kvadraten" dispenserar manipulerande siffror genom multiplikation och division eller regeln om tre. Navigatorn kan bedöma avanzar och alargar visuellt, enbart genom mätning.

Denna metod kan användas för alla avsedda bäring och avvikelser, eftersom det enda syftet är att lösa triangeln med avdelare och skala. t.ex. genom att använda vårt första exempel från Korsika till Genua, där den avsedda bäringen var norrut men fartyget faktiskt seglade nordväst, skulle navigatören ställa in avdelare på 70 miles längd och lägga den längs fjärde kvartalets vind (= SE-strålen i tondo e quadro , eftersom NV är fyra fjärdedels vindar bort från norr). Han skulle beräkna alargar och avanzar på exakt samma sätt - rita en linje till den horisontella toppen av rutnätet, mäta rutorna osv.

Tondo e quadro -enheten är mycket lik den arabiska sinuskvadranten ( Rubul mujayyab ), med hörnstrålarna som replikerar den justerbara lodlinjens roll .

Andra applikationer

Även om toleta de marteloio (och dess visuella motsvarighet, tondo e quadro ) är designade för den explicita uppgiften att återställa en avsedd kurs, kan de användas på fler sätt, för många klasser av navigeringsproblem, t.ex. att rita ut en kurs med flera -lagerändringar osv.

Triangulering

En av de intressanta tillämpningarna av regeln om marteloio är för triangulering , t.ex. bestämning av fartygets avstånd från landmärke från land. (Detta var den sista övningen i anteckningsboken för den venetianske navigatören Michael av Rhodos, som vi replikerar här.)

Exempel : Anta att ett fartyg som seglar NV ("Maestro") upptäcker ett landmärke rakt västerut ("Ponente") en kväll, men avståndet är okänt. Anta att fartyget fortsätter att segla på NW-rutten över natten, och nästa morgon, 60 mil senare, märker det att landmärket nu är västsydväst (WSW, "Ponente-Libeccio") om sin nuvarande position. Att hitta avståndet mellan landmärket från fartyget är bara en tillämpning av regeln om marteloio.

Tillämpning av regeln om marteloio för att uppskatta avståndet mellan fartyget och ett landmärke vid stranden.

För att lösa problemet, utgå från kvällspositionen ( A på kartan) och behandla avståndet mellan fartyget och landmärket (längd AB ) som avsedd kurs, och den faktiska rutten för fartyget (NW) som en avvikelse. För att räkna ut landmärkets avstånd från fartygets position på morgonen ( C ) handlar det om att behandla avståndet BC som den beräknade ritorno. Eftersom vi behöver känna till alargar för att beräkna ritorno, är detta en tvåstegsprocedur.

Lägg först märke till att NW är fyra kvartsvindar över W, så tittar du upp på toleta, i q = 4-raden, är alargarn 71 miles för varje 100 miles på NW-banan. Men fartyget seglade bara 40 miles över natten, så vi måste lösa förhållandet 71/100 = x /40, vilket med treregeln betyder x = alargar = 28,4 miles. Med andra ord, genom att övernatta NV med 40 miles från A till C, är fartyget nu 28,4 miles från sin "avsedda" kurs västerut.

Nu till ritorno. Landmärket, som noterat, är WSW om fartygets morgonposition ( C ). Så för att "återvända" till landmärket måste fartyget ändra sin bäring från sin nuvarande NV-riktning till en WSW-bäring – det vill säga 6 kvartsvindar under NV. Men toletan specificerar kvartsvindar i termer av "avsedd" riktning (i det här fallet, väst), och WSW är två kvartsvindar under väster, så vi måste titta på q = 2 raden. Det betyder att ritorno är 26 miles för varje 10 miles alargar. Eftersom alargar är 28,4 betyder det att ritorno är 26 × 2,84 = 73,84. Och där har vi det. Landmärket är 73,84 miles från fartygets morgonposition.

(För att slutföra berättelsen skulle vi kanske vilja ta reda på avståndet som landmärket var kvällen innan (dvs. från punkt A till landmärke B). Det är helt enkelt en fråga om att lägga till avanzar och avanzo i ritorno. Snabba beräkningar visar avanzar (@ q = 4, för 40 miles) är 28,4 miles (= 71 × 40/100) och avanzo di ritorno (@ q = 2 för 28,4 miles alargar), är 2,84 × 24 = 68,16. Så total avanzo = 28,4 + 68,16 = 96,56 miles. Det var avståndet mellan landmärket och fartyget kvällen innan.)

Att hitta platser

Regeln för marteloio kan också användas med avanzaren som mål, t.ex. anta att ett skepp ger sig ut i avsikt att hitta Tordesillaslinjen, meridianen som lagligen fastställts i ett fördrag från 1494 vid 370 ligor väster om Kap Verde . Fartyget behöver inte ge sig ut från Kap Verde och ständigt segla i västlig riktning för att hitta det. Snarare kan den segla ut i en mer bekväm bäring (t.ex. SW), och behandla väst som en "avsedd" kurs. Så med hjälp av marteloio-regeln kan den segla vidare tills avanzaren på den "avsedda" västra banan når 370 ligor.

Den behöver faktiskt inte ens ge sig av från Kap Verde, utan kan ge sig av från en annan plats, säg Sevilla , och använda Kap Verdes kända avstånd och bäring (se Sevilla) och regeln för marteloio för att beräkna när den äntligen har nådde Tordesillas meridian. Detta tar ett par steg. Anta att Kap Verde ( B på kartan) ligger 400 ligor sydväst om Sevilla ( A på kartan), men fartyget har för avsikt att gå rakt västerut från Sevilla för att nå Tordesillas meridian i öppet hav. Hur lång tid behöver den segla?

Att hitta Tordesillaslinjen via regeln om marteloio

Sättet att lösa detta med regeln om marteloio är att ställa problemet i omvänd riktning: behandla väst som avsett bäring och SW som den faktiska kursen. SW är fyra kvartsvindar under W, så tittar man upp toletan för q = 4, är avanzaren 71 för varje seglat 100 mil. Så om ett fartyg seglade 400 ligor på den "faktiska" SW kursen till Kap Verde, skulle det uppnå en avanzar på 284 ligor (= 71 × 4) på ​​den "avsedda" kursen västerut. Naturligtvis seglar fartyget faktiskt inte SW till Kap Verde, utan seglar W ut i öppet hav. Med andra ord, när fartyget seglar västerut från Sevilla, vet det att det behöver segla 284 ligor i västlig bäring innan det når den antydda Kap Verdes meridian (punkt C på kartan), och bör bara börja räkna de 370 ligorna till Tordesillas linje därefter. Med andra ord behöver den segla totalt 284 + 370 = 654 ligor väster om Sevilla för att nå Tordesillaslinjen (punkt D på kartan).

Även om detta specifika exempel visar flexibiliteten hos regeln om marteloio, visar det också en av dess huvudsakliga nackdelar: resultatet ignorerar helt jordens krökning, dvs det faktum att longitudmeridianlinjerna konvergerar på nordpolen och därmed smalnar av vid högre breddgrader. I motsats till vad marteloio antyder, ligger 370 ligor väster om Kap Verde inte på samma longitudmeridian som 654 ligor väster om Sevilla. Eftersom Sevilla ligger långt norr om Kap Verde, är meridianerna samlade närmare varandra på Sevillas latitud än på Kap Verdes latitud. Ett fartyg som seglar väster om Sevilla kommer faktiskt att nå den verkliga Tordesillas-meridianen (punkt T på kartan) långt innan 654 ligor seglas (punkt D ).

Regeln för marteloio låter sjömän rita rutter genom att rita plana trianglar på ett sjökort, som om världens yta vore platt. Även om detta kan vara praktiskt nog för segling begränsad till Medelhavets kompakta breddgrader, är det ganska missvisande i större skala.

Förhållande till senare regler

Relation till "ligornas regemente"

I slutet av 1400- och 1500-talen gjorde förbättringen av nautisk astronomi och införandet av latitudparalleller det möjligt för navigatörer att bestämma sin position till sjöss genom himmelsavläsningar, snarare än att förlita sig på uppskattning av seglat avstånd. Efterföljaren till regeln av marteloio var "Regiment of the Leagues" ( regimento das léguas ), som användes av portugisiska navigatörer som seglade i Atlanten. Eller, för att använda termen introducerad av William Bourne (1571), "Regeln för att höja eller lägga en grad", även känd som "Table of Leagues" eller "Regeln för att höja polen". Den skrevs först ner i den portugisiska navigationshandboken Regimento do astrolabio e do quadrante (publicerad i Lissabon ca 1509, men skriven ca 1480) Den populariserades av Martín Cortés de Albacar i hans 1551 Breve compendio la esfera y del arte de navegar .

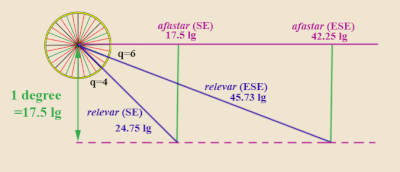
"Ligornas regemente" skiljer sig inte mycket från regeln i marteloio. Förbundsregementet betraktar alltid den väst-östliga bäringen som den "avsedda kursen" och åtgärder sätter avvikelser från den. Mer specifikt tar ligatabellen hänsyn till ett fast värde på alargar – satt till 1 latitudgrad (eller, i tidens mätningar, 17,5 (portugisiska) ligor , eller motsvarande 70 (italienska) miles ). Den ger sedan för varje enskild fjärdedel av seglingsriktningen (alltid betecknad som fjärdedelar bort från nord-syd-axeln, snarare än bort från den avsedda kursen), relevaren och afastar . Relevaren är antalet ligor på den faktiska kursen som ett fartyg måste segla för att täcka den förinställda 1 latitudgraden (17,5 ligor av alargar från startparallellen). Afastar är bara motsvarande avanzar på den väst-östliga bäringen .

Illustration av "Ligornas regemente"

Exempel : Antag att ett fartyg ger sig ut på en öst-sydöstlig (ESE) bäring. Det är sex kvartsvindar ovanför syd (kom ihåg: till skillnad från marteloio, mäter Regiment of the Leagues alltid kvartsvindar bort från nord–sydlig meridian). Om man tittar på valfritt regemente i ligatabellen (t.ex. Martín Cortés de Albacar , 1551), för q = 6, ger tabellen relevaren som 45 11 ⁄ 15 ligor och afastar som 42 1 ⁄ 4 ligor. Detta innebär att ett fartyg som seglar på ESE-bäringen måste segla 45,73 ligor för att täcka en latitud (17,5 ligor av alargar från den östliga bäringen, för att använda marteloio-språket), och motsvarande afastar ( avanzar i marteloio-termer) kommer att vara 42,25 ligor.

Om fartyget istället hade lagt ut på en SE-riktning, det vill säga fyra kvartsvindar ovanför syd, är motsvarande värden för Regiment of the Leagues-tabellen vid q = 4 relevar = 24 3 ⁄ 4 och afastar = 17 1 ⁄ 2 .

Lägg märke till att SE-bäringen når 1 grads alargar snabbare (dvs. mindre relevar ) än ESE-bäringen och kommer att ha mindre afastar (närmare N–S-meridianen).

Matematiskt,

relevar = 17,5/cos θ
afastar = 17,5 × tan θ

där θ = 11,25 × antal kvartsvindar bort från nord-syd-axeln.

Trots skillnaden i terminologi, särskilt användningen av latitudgrader, är regeln om marteloio och Regiment of the Leagues väldigt lika – de handlar båda om att lösa trianglar på ett plandiagram. Fördelen med regementet framför marteloio är införandet av latitudparalleller i tabellen, så att positionen kan kontrolleras genom astronomisk observation (via kvadrant , astrolabium , etc.), och inte helt måste förlita sig på sjömans uppskattningar av avstånd och riktning.

Med regementet kan geografiska koordinater också användas för att styra navigeringen. Till exempel är sökningen efter Todesillas-linjen (meridian 370 ligor väster om Kap Verde) mycket förenklad med hänvisning till en exakt latitud. Anta till exempel att två fartyg avgår från Kap Verde (17° N), det ena i en väst-nordvästlig bäring (WbN, det vill säga en fjärdedel ovanför väster, eller q = 7 från nordaxeln), det andra i en väst- nordvästlig bäring (WNW, två fjärdedelar ovanför väst, eller q = 6 från nordaxeln). Med hjälp av Regiment of the Leagues är det möjligt att beräkna de exakta breddgraderna när de kommer att korsa Tordesillas meridian – dela helt enkelt 370 ligor västerut med den antydda afastar vid de olika bäringarna. WbN-skeppet kommer att nå meridianen när det uppnår latitud 21° 21' N, medan WNW-fartyget når det när det uppnår latitud 29° N. Så istället för att räkna ligor med timglas och hastighetsavläsningar, kan fartygen bara behålla bäring, och ta periodiska astronomiska observationer för att bedöma deras latitud.

Relation till "traversesegling"

Toleta de marteloio är förfäder till det moderna "traversbordet" som används i modernare navigering. I den moderna nomenklaturen är traversen "den krokiga vägen som görs av ett fartyg när det seglar i flera på varandra följande riktningar" och att lösa traversen är "metoden att hitta en enda kurs och ett avstånd som skulle föra ett fartyg till samma plats som två eller fler kurser och distanser”. I marteloio-språket, när man "löser traversen", är den kända informationen som ges "det faktiska förloppet" och "ritorno", medan de okända är den "avsedda bäringen" och "total avanzo".

Traverstabeller använder tre värden för vart och ett av de krokiga kurssegmenten – avståndet (avstånd), latitudskillnaden (D.Lat., rörelse längs N–S-axeln) och avgången ( avstånd, rörelse längs österaxeln) , de två senare beräknas med formlerna:

Latitudskillnad = avstånd × cos θ
Avgång = avstånd × sin θ

där θ är vinkelskillnaden för kursen från N–S-axeln om värdena för θ är mindre än 45°; om vinkeln däremot överstiger 45°, så θ som skillnadsvinkeln från E–W-axeln, och formlerna vänds, dvs. Latitudeskillnadens formel blir Avgång, och Avgångsformeln är Skillnaden mellan Latitud). Eller, ännu enklare, beräkna θ som skillnadsvinkeln från närmaste huvudvind (N, S, E, W), kör formlerna och placera sedan det större talet i lämplig kolumn (D.Lat. eller Dep.) .

För varje kurssegment infogar navigatören den relevanta trion (Dist., D.Lat., Dep.) och kan beräkna den implicita bäringen från början till slutpunkten och avståndet som kompenseras för den bäringen. Han kombinerar sedan, genom addition och subtraktion, alla skillnader mellan latitud och avgång, för att få den övergripande skillnaden mellan latitud och avgång, och konverterar den tillbaka till den totala bäringen och avståndet.

Manuskriptkällor

Ramon Llulls suggestiva kommentarer från 1295, är den tidigaste kända referensen till marteloio daterad 1390, i inventeringen av boet efter modern till en viss Oberto Foglieto av Genua, där en post lyder unum martelogium....item carta una pro navegando . Det första tydliga utseendet och förklaringen är den venetianske kaptenen Andrea Biancos atlas från 1436 . Andra tidiga manuskript har sedan dess hittats som relaterar till regeln om marteloio, inkluderar:

Toleta de marteloio och en åttavinds tondo e quadro , från sid. 47 i Cornaro Atlas (ca 1489)

Anteckningar

Externa resurser

  • Altante Bianco, 1436 på Internetculturale.it; Högre upplösning på Geoweb.sbn.venezia.it.
  • McGee, D. et al. (2003 och framåt) Michael av Rhodos: En medeltida sjöfarare och hans manuskriptwebbplats ( tillträde 20 juli 2011). (ursprungligen värd av Dibner Institute for the History of Science and Technology vid MIT , nu värd av Museo Galileo Institute och Museum of the History of Science i Florens, Italien)
  • Aczel, AD (2001) Kompassens gåta: uppfinningen som förändrade världen New York: Harcourt.
  • Albertis, EA (1893) Le construzioni navale e l'arte della navigazione al tempo di Cristoforo Colombo , Pat IV, vol. 1 av Raccolta di Documenti e Studi pubblicati dalla Reale Commissione Colombiana pel quarto Centenario della scoperta dell'America . Rom: Ministero della Pubblica Istruzione.
  • Albuquerque, L. de (1970) "A navegação astronomica", i A. Cortesão, redaktör, 1969–70, História da cartografia portuguesa , vol. 2. Lissabon: Junta de Investigações do Ultramar, sid. (som återgivits 1975, Estudos de História , Vol. 3. Coimbra: UC Biblioteca Geral online )
  • Albuquerque, Luís de (1973) "O Tratado de Tordesilhas e dificuldades técnicas da sua aplicação rigorosa" i El Tratado de Tordesillas y su Proyeccion , vol. 1, s. 119–366. (Som omtryckt 1974, Estudos de História , Vol. 2. Coimbra: UC Biblioteca Geral. s. 221p56
  • Breusing, A. (1881) "La toleta de Martelojo und die loxodromischen Karten", Zeitschrift für wissenschaftliche Geographie , vol. II, Pt. 1 ( s. 129–33 ), Pt. 2 ( s. 180–95 ).
  • Brummelen, G. (2010) "Clear Sailing with Trigonometry" i D. Jardine och A. Shell-Gellasch , redaktörer, Mathematical Time Capsules: Historical modules for the mathematics classroom . Mathematical Association of America.
  • Campbell, T. (1987) "Portolan diagram från det sena trettonde århundradet till 1500", i JB Harley och D. Woodward, redaktörer, The History of Cartography, Vol. 1 – Kartografi i det förhistoriska, antika och medeltida Europa och Medelhavet . Chicago: University of Chicago Press, s. 371–63 online (PDF)
  • Cortesão, A. (1969) Portugisisk kartografis historia . Coimbra: Junta de Investigações do Ultramar
  • Cotter, CH (1978) "Tidiga tabellformade, grafiska och instrumentella metoder för att lösa problem med flygsegling", Revista da Universidade de Coimbra, Vol. 26, s. 3–20 offprint
  • D'Avezac, MAP Marquis (1874) Aperçus historiques sur la rose des vents: lettre à Monsieur Henri Narducci . Rom: Civelli online
  • Desimoni, C. (1888) "Le carte nautiche italiane del Medio Evo, a proposito di un libro del prof. Fischer", Atti della Società ligure di storia patria , vol. 19, s. 225–66.
  • Diffie, Bailey W. och George D. Winius (1977) Foundations of the Portuguese empire, 1415–1580 Minneapolis, MN: University of Minnesota Press.
  • Edson, E. (2007) The World Map, 1300–1492: the persistent of tradition and transformation . Baltimore, MD: Johns Hopkins University Press.
  • Formaleoni, Vicenzio (1783) Saggio sulla Nautica antica de' Veneziani, con una illustrazione d'alcune carte idrografiche antiché della Biblioteca di S. Marco, che dimonstrano l'isole Antille prima della scoperta di Cristoforo Colombo . Venedig. uppkopplad
  • Gelcich, E. (1892) "I primi passi della scienza nautica", Rivista Marittima , Vol. 25, s. 71–102
  • Kelley, JE (2000) Analog och digital navigering under den sena medeltiden , Melrose Park, Pa.: Sometime Publishers
  • Kelley, JE (1995) "Perspectives on the Origins and Use of Portolan Charts", Cartographica , vol. 32 (3), s. 1–16. uppkopplad
  • Kretschmer, K. (1909) Die italienischen Portolane des Mittelalters: Ein Beitrag zur Geschichte der Kartographie und Nautik . Berlin: Mittler und Sohn
  • Long, PI, D. McGee och AM Stahl, redaktörer, (2009) The Book of Michael of Rhodes: A fifteenth-century manuscript . 3 volymer, Cambridge, Mass: MIT Press.
  • Masiero, F. (1984) "La raxon de marteloio", Studi veneziani , vol. 8, s. 393–412.
  • Merrifield, J. (1883) Treatise on Navigation . London: Spottiswoode. uppkopplad
  • Morelli, Jacopo (1810) Lettera rarissima di Cristoforo Colombo . Bassano: Stamperia Remondiniana online
  • Nordenskiöld, Adolf Erik (1897) Periplus: An Essay on the Early History of Charts and Sailing Directions , tr. Frances A. Bather, Stockholm: Norstedt.
  • Parry, JH (1974) The Discovery of the Sea , 1984 års upplaga, Berkeley: University of California Press. uppkopplad
  • Ramon Llull (1305) Ars magna generalis et ultima , 1517 års upplaga, online , esp. Del 10, "De Navigatione", fo. 93, sid. 213
  • Ramon Llull (1295) L'arbre de ciència , 1635 latinsk ed: Arbor scientiæ venerabilis et cælitvs illuminati patris Ravmvndi Lvllii Maiorieensis Lyon: Pillehotte. uppkopplad
  • Randles, WGL "(1998) The Emergence of Nautical Astronomy in Portugal in the XVth Century", Journal of Navigation , Vol. 51, s. 46–57.
  • Rossi, F. (2009) "Introduktion" till volym 2 av Long, McGee och Stalh, redaktörer, Book of Michael of Rhodes . ( online )
  • Ruge, S. (1900) "Der Periplus Nordenskiölds", Deutsche geographische Blätter Vol. 23, nr 4, s. 161–228
  • Sezgin, F. (2007) Mathematical Geography and Cartography in Islam and Their Continuation in the Occident . Institutet för historien om arabisk-islamisk vetenskap
  • Taylor, EGR (1950) "Five Centuries of Dead Reckoning", Journal of Navigation , Vol. 3, s. 280–85.
  • Taylor, EGR (1956) The Haven-Finding Art: A history of navigation from Odysseus to Captain Cook , 1971 ed., London: Hollis and Carter.
  • Taylor, EGR (1960) "Mathematics and the Navigator in the Thirteenth Century", Journal of Navigation , Vol. 13, s. 1–12.
  • Toaldo, Giuseppe (1782) "Lettera a sua Eccellenza il. Sig. Cav. Giacopo Nani, contenente la spiegazione d'un antica Regola di navigare practicata da' Veneziani , Saggi di studi Veneti Venedig: Storti. s. 40–61
  • Vernet, J. (2008) "The Scientific World of the Crown of Aragon under James I" i Ramon Llull och Islam, början på dialog . Barcelona: IEMed., s. 99–114.
  • Waters, DW (1988) "Reflektioner över vissa navigerings- och hydrografiska problem under 1600-talet relaterade till Bartolomeu Dias resa", Revista da Universidade de Coimbra , Vol. 34, s. 275 347. offprint
Hämtad från " https://en.wikipedia.org/w/index.php?title=Rule_of_marteloio&oldid=1129933566 "