Pentomino

De 12 pentominoerna kan bilda 18 olika former, varav 6 av dem (de kirala pentominoerna) är spegelvända.

(eller 5-omino ) kommer från det grekiska ordet för ' 5 ' och " domino ", en pentomino (eller 5-omino ) är en polyomino av ordningen 5, det vill säga en polygon i planet gjord av 5 lika stora rutor anslutna kant-till- kant. När rotationer och reflektioner inte anses vara distinkta former, finns det 12 olika fria pentominoer. När reflektioner anses vara distinkta finns det 18 ensidiga pentominoer. När rotationer också anses vara distinkta finns det 63 fasta pentominoer.

Pentomino pussel och spel är populära inom rekreationsmatematik . Vanligtvis videospel som Tetris -imitationer och Rampart spegelreflektioner vara distinkta och använder därför hela uppsättningen av 18 ensidiga pentominoer.

Var och en av de tolv pentominoerna uppfyller Conway-kriteriet ; därför är varje pentomino kapabel att lägga till plattor på planet . Varje kiral pentomino kan kakla planet utan att reflekteras.

Historia

Jämförelse av märkningsscheman för de 12 möjliga pentominoformerna. Den första namnkonventionen är den som används i den här artikeln. Den andra metoden är Conways.

Det tidigaste pusslet som innehöll en komplett uppsättning pentominoer dök upp i Henry Dudeneys bok, The Canterbury Puzzles , publicerad 1907. De tidigaste plattsättningarna av rektanglar med en komplett uppsättning pentominoer dök upp i Problemist Fairy Chess Supplement 1935, och ytterligare problem med plattsättningen utforskades i PRCS, och dess efterföljare, Fairy Chess Review . Pentominoes definierades formellt av den amerikanske professorn Solomon W. Golomb med början 1953 och senare i sin bok från 1965 Polyominoes: Puzzles, Patterns, Problems, and Packings . De introducerades för allmänheten av Martin Gardner i hans kolumn Mathematical Games i oktober 1965 i Scientific American . Golomb myntade termen "pentomino" från antikens grekiska πέντε / pénte , "fem", och -omino för domino , och tolkade fantasifullt "d-" för "domino" som om det vore en form av det grekiska prefixet "di- "(två). Golomb döpte de 12 fria pentominoerna efter bokstäver i det latinska alfabetet som de liknar.

John Horton Conway föreslog ett alternativt märkningsschema för pentominoer, med O istället för I, Q istället för L, R istället för F och S istället för N. Likheten med bokstäverna är mer ansträngd, särskilt för O pentomino, men detta schemat har fördelen av att använda 12 på varandra följande bokstäver i alfabetet. Det används av konventionen när man diskuterar Conways Game of Life , där man till exempel talar om R-pentomino istället för F-pentomino.

Symmetri

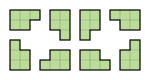
• F, L, N, P och Y kan orienteras på 8 sätt: 4 genom rotation och 4 till för spegelbilden. Deras symmetrigrupp består endast av identitetskartläggningen .
• T och U kan orienteras på 4 sätt genom rotation. De har en reflektionsaxel i linje med rutnätslinjerna. Deras symmetrigrupp har två element, identiteten och reflektionen i en linje parallell med kvadraternas sidor.
• V och W kan också orienteras på 4 sätt genom rotation. De har en reflektionssymmetriaxel i 45° mot rutnätslinjerna. Deras symmetrigrupp har två element, identiteten och en diagonal reflektion.
• Z kan orienteras på 4 sätt: 2 genom rotation och 2 till för spegelbilden. Den har punktsymmetri, även känd som rotationssymmetri av ordning 2. Dess symmetrigrupp har två element, identiteten och 180°-rotationen.
• Jag kan orienteras på 2 sätt genom rotation. Den har två axlar för reflektionssymmetri, båda i linje med rutnätslinjerna. Dess symmetrigrupp har fyra element, identiteten, två reflektioner och 180°-rotationen. Det är den dihedriska gruppen av ordning 2, även känd som Klein-fyragruppen .
• X kan endast orienteras på ett sätt. Den har fyra axlar för reflektionssymmetri, i linje med rutnätslinjerna och diagonalerna, och rotationssymmetri av ordning 4. Dess symmetrigrupp, den dihedriska gruppen av ordning 4, har åtta element.

Pentominoerna F, L, N, P, Y och Z är kirala ; genom att addera deras reflektioner (F′, J, N′, Q, Y′, S) kommer antalet ensidiga pentominoer till 18. Om rotationer också anses vara distinkta, räknas pentominoerna från den första kategorin åtta gånger, de från de följande tre kategorierna (T, U, V, W, Z) räknas fyra gånger, I räknas två gånger och X räknas bara en gång. Detta resulterar i 5×8 + 5×4 + 2 + 1 = 63 fasta pentominoer.

Till exempel är de åtta möjliga orienteringarna för pentominoerna L, F, N, P och Y som följer:

    

För 2D-figurer i allmänhet finns det ytterligare två kategorier:

• Att vara orienterbar på två sätt genom en rotation på 90°, med två reflektionssymmetriaxlar, båda i linje med diagonalerna. Denna typ av symmetri kräver åtminstone en heptomino .
• Att vara orienterbar på 2 sätt, som är varandras spegelbilder, till exempel ett hakkors . Denna typ av symmetri kräver minst en octomino .

Konstruera rektangulära dimensioner

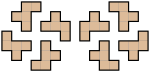
Ett vanligt pentomino-pussel är att kakla en rektangulär låda med pentominoerna, dvs täcka den utan överlappning och utan mellanrum. Var och en av de 12 pentominoerna har en yta på 5 enhetsrutor, så lådan måste ha en yta på 60 enheter. Möjliga storlekar är 6×10, 5×12, 4×15 och 3×20.

Fallet 6×10 löstes först 1960 av Colin Brian Haselgrove och Jenifer Haselgrove . Det finns exakt 2339 lösningar, exklusive triviala variationer som erhålls genom rotation och reflektion av hela rektangeln, men inklusive rotation och reflektion av en delmängd av pentominoer (vilket ibland ger en ytterligare lösning på ett enkelt sätt). 5×12-lådan har 1010 lösningar, 4×15-lådan har 368 lösningar och 3×20-lådan har bara 2 lösningar (en visas i figuren och den andra kan erhållas från lösningen som visas genom att rotera, som helhet, blocket som består av L, N, F, T, W, Y och Z pentominoer).

Ett något lättare (mer symmetriskt) pussel, rektangeln 8×8 med ett 2×2 hål i mitten, löstes av Dana Scott så långt tillbaka som 1958. Det finns 65 lösningar. Scotts algoritm var en av de första tillämpningarna av ett bakåtspårande datorprogram. Variationer av detta pussel gör att de fyra hålen kan placeras i valfri position. En av de externa länkarna använder denna regel. De flesta sådana mönster är lösbara, med undantag för att placera varje par av hål nära två hörn av brädet på ett sådant sätt att båda hörnen bara kunde passas av en P-pentomino, eller tvinga en T-pentomino eller U-pentomino i en hörn så att ytterligare ett hål skapas.

Effektiva algoritmer har beskrivits för att lösa sådana problem, till exempel av Donald Knuth . Dessa pentomino-pussel körs på modern hårdvara och kan nu lösas på bara några sekunder.

Pentominosetet är det enda fria polyominosetet som kan packas i en rektangel, med undantag för de triviala monomino- och dominouppsättningarna , som var och en endast består av en enda rektangel.

Fylla lådor

En pentakub är en polykub med fem kuber. Av de 29 pentakuberna är exakt tolv pentakuber platta (1-lager) och motsvarar de tolv pentominoerna som strängpressats till ett djup av en kvadrat.

Ett pentacube-pussel eller 3D pentomino-pussel innebär att fylla en 3-dimensionell låda med 12 platta pentacubes, dvs täcka den utan överlappning och utan luckor. Eftersom varje pentakub har en volym på 5 enhetskuber måste lådan ha en volym på 60 enheter. Möjliga storlekar är 2×3×10 (12 lösningar), 2×5×6 (264 lösningar) och 3×4×5 (3940 lösningar). Följande är en lösning för varje fall.

Alternativt kan man också överväga kombinationer av fem kuber som i sig är 3D, dvs inte är en del av ett lager av kuber. Men förutom de 12 extruderade pentominoerna, blir 6 uppsättningar kirala par och 5 stycken totalt 29 stycken, vilket resulterar i 145 kuber, vilket inte kommer att göra en 3D-låda (eftersom 145 bara kan vara 29×5×1, vilket inte -platta pentominoer kan inte passa in).

Brädspel

Det finns skicklighetsspel baserade helt på pentominoer. Sådana spel kallas ofta helt enkelt "Pentominoes".

Ett av spelen spelas på ett 8×8-rutnät av två eller tre spelare. Spelare turas om att placera pentominoer på brädet så att de inte överlappar befintliga brickor och ingen bricka används mer än en gång. Målet är att vara den sista spelaren som lägger en bricka på brädet. Denna version av Pentominoes kallas "Golomb's Game".

Tvåspelarversionen har lösts svagt 1996 av Hilarie Orman. Det visade sig vara en vinst för första spelare genom att undersöka omkring 22 miljarder styrelsepositioner.

Pentominoer och liknande former är också grunden för en rad andra kakelspel, mönster och pussel. Till exempel spelas det franska brädspelet Blokus med 4 färgade uppsättningar polyominoer , var och en bestående av varje pentomino (12), tetromino (5), triomino (2), domino (1) och monomino (1). Precis som spelet Pentominoes är målet att använda alla dina brickor, och en bonus ges om monomino spelas på sista draget. Spelaren med minst kvarvarande block vinner.

Spelet Cathedral är också baserat på polyominoer .

Parker Brothers släppte ett pentomino-brädspel för flera spelare som heter Universe 1966. Dess tema är baserat på en raderad scen från 1968 filmen 2001: A Space Odyssey där en astronaut spelar ett pentominospel för två spelare mot HAL 9000-datorn ( en scen med en annan astronaut som spelade schack behölls). Framsidan av brädspelslådan innehåller scener från filmen samt en bildtext som beskriver det som "framtidens spel". Spelet kommer med fyra uppsättningar pentominoer i rött, gult, blått och vitt. Brädan har två spelbara områden: en basyta på 10x10 för två spelare med ytterligare 25 rutor (två fler rader med 10 och en förskjuten rad med fem) på varje sida för fler än två spelare.

Speltillverkaren Lonpos har ett antal spel som använder samma pentominoer, men på olika spelplan. Deras 101 Game har ett 5 x 11 plan. Genom att ändra formen på planet kan tusentals pussel spelas, även om endast ett relativt litet urval av dessa pussel finns i tryck.

Litteratur

Pentominoes var med i en framstående delintrig av Arthur C. Clarkes roman Imperial Earth från 1975 . Clarke skrev också en uppsats där han beskrev spelet och hur han fastnade för det.

De var också med i Blue Ballietts Chasing Vermeer , som publicerades 2003 och illustrerades av Brett Helquist , såväl som dess uppföljare, The Wright 3 och The Calder Game .

I New York Times korsord för den 27 juni 2012 var ledtråden för ett 11-bokstavsord med 37 tvärs över "Komplett uppsättning av 12 former bildade av detta pussels svarta rutor."

Videospel

• Tetris var inspirerad av pentomino-pussel, även om den använder fyra-blocks tetrominoer. Vissa Tetris-kloner och varianter, som spelet 5s som ingår i Plan 9 från Bell Labs och Magical Tetris Challenge , använder pentominoer.
• Daedalian Opus använder pentomino-pussel genom hela spelet.

Se även

Föregående och nästa beställning

• Tetromino
• Hexomino

Andra

• Kakelpussel
• Katedralens brädspel
• Solomon W. Golomb

Anteckningar

• Chasing Vermeer , med information om boken Chasing Vermeer och en klick-och-dra pentomino-bräda.
•   Pritchard, DB (1982). "Golombs spel". Hjärnspel . Penguin Books Ltd. s. 83–85. ISBN 0-14-00-5682-3 .

externa länkar

• Pentomino-konfigurationer och lösningar En uttömmande lista över lösningar på många av de klassiska problemen som visar hur varje lösning förhåller sig till de andra.