Hör formen av en trumma

Matematiskt idealiska trummor med membran av dessa två olika former (men annars identiska) skulle låta likadant, eftersom egenfrekvenserna alla är lika, så klangspektra skulle innehålla samma övertoner. Detta exempel konstruerades av Gordon, Webb och Wolpert. Lägg märke till att båda polygonerna har samma area och omkrets.

Att höra formen på en trumma är att härleda information om formen på trumskinnet från ljudet det gör, dvs från listan över övertoner , genom användning av matematisk teori.

"Kan man höra formen av en trumma?" är titeln på en artikel från 1966 av Mark Kac i American Mathematical Monthly som gjorde frågan känd, även om just denna frasering kommer från Lipman Bers . Liknande frågor kan spåras ända tillbaka till fysikern Arthur Schuster 1882. För sin tidning fick Kac Lester R. Ford Award 1967 och Chauvenet-priset 1968.

Frekvenserna vid vilka ett trumskinn kan vibrera beror på dess form. Helmholtz -ekvationen beräknar frekvenserna om formen är känd. Dessa frekvenser är egenvärdena för Laplacian i rymden. En central fråga är om formen kan förutsägas om frekvenserna är kända; till exempel om en Reuleaux-triangel kan kännas igen på detta sätt. Kac medgav att han inte visste om det var möjligt för två olika former att ge samma uppsättning frekvenser. Frågan om frekvenserna bestämmer formen besvarades slutligen nekande i början av 1990-talet av Gordon, Webb och Wolpert.

Formellt uttalande

Mer formellt är trumman tänkt som ett elastiskt membran vars gräns är fastklämd. Den representeras som en domän D i planet . Beteckna med λ _n Dirichlet -egenvärdena för D : det vill säga egenvärdena för Dirichlet- problemet för Laplacian :

${\begin{cases}\Delta u+\lambda u=0\\u|_{\partial D}=0\end{cases}}$

Två domäner sägs vara isospektrala (eller homofoniska) om de har samma egenvärden. Termen "homofonisk" är motiverad eftersom Dirichlets egenvärden är just de fundamentala toner som trumman kan producera: de uppträder naturligt som Fourier-koefficienter i lösningsvågekvationen med klämd gräns .

Därför kan frågan omformuleras som: vad kan man sluta sig till om D om man bara känner till värdena på λ _n ? Eller mer specifikt: finns det två distinkta domäner som är isospektrala?

Besläktade problem kan formuleras för Dirichlet-problemet för Laplacian på domäner i högre dimensioner eller på Riemannska grenrör , såväl som för andra elliptiska differentialoperatorer som Cauchy-Riemann-operatorn eller Dirac-operatorn . Andra gränsvillkor förutom Dirichlet-villkoret, såsom Neumann-gränsvillkoret , kan införas. Se spektralgeometri och isospektral som relaterade artiklar.

Svaret

En-parameter familj av isospektrala trummor

Egenmoder och motsvarande egenvärden för Laplace-operatorn på GWW-domänerna

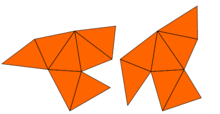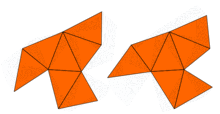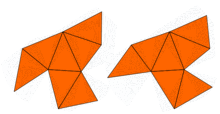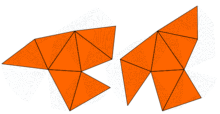
1964 observerade John Milnor att ett teorem om gitter på grund av Ernst Witt antydde att det fanns ett par 16-dimensionella platta tori som har samma egenvärden men olika former. Problemet i två dimensioner förblev dock öppet fram till 1992, då Carolyn Gordon , David Webb och Scott Wolpert, baserat på Sunada-metoden , konstruerade ett par regioner i planet som har olika former men identiska egenvärden. Områdena är konkava polygoner . Beviset på att båda regionerna har samma egenvärden använder symmetrierna hos Laplacian. Denna idé har generaliserats av Buser, Conway, Doyle och Semmler som konstruerade många liknande exempel. Så svaret på Kacs fråga är: för många former kan man inte höra trummans form helt . Viss information kan dock antas.

Å andra sidan bevisade Steve Zelditch att svaret på Kacs fråga är positivt om man inför begränsningar för vissa konvexa plana områden med analytisk gräns. Det är inte känt om två icke-konvexa analytiska domäner kan ha samma egenvärden. Det är känt att uppsättningen av domäner som är isospektrala med en given är kompakt i C ^∞ topologin. Dessutom är sfären (till exempel) spektralt stel, enligt Chengs egenvärdesjämförelsesats . Det är också känt, genom ett resultat av Osgood, Phillips och Sarnak, att modulutrymmet för Riemann-ytor av ett givet släkte inte tillåter ett kontinuerligt isospektralt flöde genom någon punkt och är kompakt i Fréchet-Schwartz-topologin.

Weyls formel

Huvudartikel: Weyl law

Weyls formel säger att man kan sluta sig till arean A av trumman genom att räkna hur snabbt λ _n växer. Vi definierar N ( R ) som antalet egenvärden som är mindre än R och vi får

$A=\omega _{d}^{-1}(2\pi )^{d}\ lim _{R\to \infty }{\frac {N(R)}{R^{d/2}}},$

där d är dimensionen och $\omega _{d}$ är volymen av den d -dimensionella enhetsbollen. Weyl förmodade också att nästa term i approximationen nedan skulle ge omkretsen av D . Med andra ord, om L betecknar längden på omkretsen (eller ytarean i högre dimension), så bör man ha

$N(R)=(2\pi )^{-d}\omega _{d}AR^{d/2}\mp {\frac {1}{4}}(2\pi )^{ -d+1}\omega _{d-1}LR^{(d-1)/2}+o(R^{(d-1)/2}).$

För en jämn gräns, bevisades detta av Victor Ivrii 1980. Förgreningsröret är inte heller tillåtet att ha en tvåparametersfamilj av periodiska geodesiker, som en sfär skulle ha.

Weyl-Berry-förmodan

För icke-släta gränser antog Michael Berry 1979 att korrigeringen skulle vara av storleksordningen

$R^{D/2},$

där D är Hausdorff-dimensionen av gränsen. Detta motbevisades av J. Brossard och R. A. Carmona, som då föreslog att man skulle ersätta Hausdorff-dimensionen med den övre boxdimensionen . I planet bevisades detta om gränsen har dimension 1 (1993), men mest motbevisad för högre dimensioner (1996); båda resultaten är av Lapidus och Pomerance .

Se även

• Gassmann trippel
• Isospektral
• Spektral geometri
• Vibrationer av ett cirkulärt membran
• en förlängning till itererade funktionssystemfraktaler

Anteckningar

• Abikoff, William (januari 1995), "Remembering Lipman Bers" (PDF) , Notices of the AMS , 42 (1): 8–18
•   Brossard, Jean; Carmona, René (1986). "Kan man höra dimensionen av en fraktal?" . Comm. Matematik. Phys . 104 (1): 103–122. Bibcode : 1986CMaPh.104..103B . doi : 10.1007/BF01210795 . S2CID 121173871 .
• Buser, Peter ; Conway, John ; Doyle, Peter; Semmler, Klaus-Dieter (1994), "Some planar isospectral domains", International Mathematics Research Notices , 1994 (9): 391–400, doi : 10.1155/S1073792894000437
•   Chapman, SJ (1995). "Trummor som låter likadant". American Mathematical Monthly . 102 (februari): 124–138. doi : 10.2307/2975346 . JSTOR 2975346 .
•   Giraud, Olivier; Thas, Koen (2010). "Höra former av trummor - matematiska och fysiska aspekter av isospektralitet". Recensioner av modern fysik . 82 (3): 2213–2255. arXiv : 1101.1239 . Bibcode : 2010RvMP...82.2213G . doi : 10.1103/RevModPhys.82.2213 . S2CID 119289493 .
• Gordon, Carolyn ; Webb, David (1996), "You can't hear the shape of a drum", American Scientist , 84 (januari–februari): 46–55, Bibcode : 1996AmSci..84...46G
•   Gordon, C .; Webb, D .; Wolpert, S. (1992), "Isospectral plane domains and surfaces via Riemannian orbifolds", Inventiones Mathematicae , 110 (1): 1–22, Bibcode : 1992InMat.110....1G , doi : 10.1007/BF012, S2C2012, S2C2012, 52C2012, 52C2012 , 52C2012 , 52C2012
•   Ivrii, V. Ja. (1980), "Den andra termen av den spektrala asymptotiken för en Laplace-Beltrami-operatör på grenrör med gräns", Funktsional. Anal. I Prilozhen , 14 (2): 25–34, doi : 10.1007/BF01086550 , S2CID 123935462 (på ryska ).
•   Kac, Mark (april 1966). "Kan man höra formen av en trumma?" (PDF) . American Mathematical Monthly . 73 (4, del 2): ​​1–23. doi : 10.2307/2313748 . JSTOR 2313748 .
•   Lapidus, Michel L. (1991), "Kan man höra formen av en fraktal trumma? Partial resolution of the Weyl-Berry conjecture", Geometric Analysis and Computer Graphics (Berkeley, CA, 1988) , Math. Sci. Res. Inst. Publ., New York: Springer, 17 (17): 119–126, doi : 10.1007/978-1-4613-9711-3_13 , ISBN 978-1-4613-9713-7
• Lapidus, Michel L. (1993), "Vibrationer av fraktala trummor, Riemann-hypotesen , vågor i fraktala medier och Weyl-Berry-förmodan", i BD Sleeman; RJ Jarvis (red.), Ordinära och partiella differentialekvationer, Vol IV, Proc. Tolfte Internat. Konf. (Dundee, Skottland, Storbritannien, juni 1992) , Pitman Research Notes in Math. Series, vol. 289, London: Longman and Technical, s. 126–209
• Lapidus, ML; van Frankenhuysen, M. (2000), Fractal Geometry and Number Theory: Complex dimensions of fraktal strings and nolls of zeta functions , Boston: Birkhauser . (Reviderad och förstorad andra upplagan kommer 2005.)
•   Lapidus, Michel L.; Pomerance, Carl (1993), "Riemann zeta-funktionen och den endimensionella Weyl-Berry-förmodan för fraktala trummor", Proc . London Math. Soc. , Serie 3, 66 (1): 41–69, CiteSeerX 10.1.1.526.854 , doi : 10.1112/plms/s3-66.1.41
•   Lapidus, Michel L.; Pomerance, Carl (1996), "Motexempel till den modifierade Weyl-Berry-förmodan om fraktala trummor", Math. Proc. Cambridge Philos. Soc. , 119 (1): 167–178, Bibcode : 1996MPCPS.119..167L , doi : 10.1017/S0305004100074053 , S2CID 33567484
•    Milnor, John (1964), "Eigenvalues ​​of the Laplace operator on certain manifolds", Proceedings of the National Academy of Sciences of the United States of America , 51 (4): 542ff, Bibcode : 1964PNAS...51..542M , doi : 10.1073/pnas.51.4.542 , PMC 300113 , PMID 16591156
•   Sunada, T. (1985), "Riemannska beläggningar och isospektrala grenrör", Ann. av matte. , 2, 121 (1): 169–186, doi : 10.2307/1971195 , JSTOR 1971195
•   Zelditch, S. (2000), "Spectral determination of analytic bi-axisymmetric plane domains", Geometric and Functional Analysis , 10 (3): 628–677, arXiv : math/9901005 , doi : 10.1007/PL3007/PL300 4007/ PL300 , S216C 4000

externa länkar

• Simulering som visar lösningar av vågekvationen i två isospektrala trummor
• Isospektrala trummor av Toby Driscoll vid University of Delaware
• Några plana isospektrala domäner av Peter Buser, John Horton Conway , Peter Doyle och Klaus-Dieter Semmler
  • 3D-rendering av Buser-Conway-Doyle-Semmler homofoniska trummor
• Drums That Sound Alike av Ivars Peterson på Mathematical Association of Americas webbplats
• Weisstein, Eric W. "Isospektrala grenrör" . MathWorld .
• Benguria, Rafael D. (2001) [1994], "Dirichlet eigenvärde" , Encyclopedia of Mathematics , EMS Press