Taits gissning
Inom matematiken säger Taits gissning att "Varje 3-kopplad plan kubisk graf har en Hamiltonsk cykel (längs kanterna) genom alla dess hörn ". Det föreslogs av PG Tait ( 1884 ) och motbevisades av WT Tutte ( 1946 ), som konstruerade ett motexempel med 25 ytor, 69 kanter och 46 hörn. Flera mindre motexempel, med 21 ytor, 57 kanter och 38 hörn, visade sig senare vara minimala av Holton & McKay (1988) . Villkoret att grafen ska vara 3-regelbunden är nödvändig på grund av polyedrar som den rombiska dodekaedern , som bildar en tvådelad graf med sex grader-fyra hörn på ena sidan och åtta grader-tre hörn på den andra sidan; eftersom varje Hamiltonsk cykel skulle behöva alternera mellan de två sidorna av bipartitionen, men de har ojämnt antal hörn, är den rombiska dodekaedern inte Hamiltonsk.
Gissningen var betydande, för om den var sann, skulle den ha antydt fyrafärgssatsen : som Tait beskrev, är fyrfärgsproblemet ekvivalent med problemet med att hitta 3-kantsfärgningar av brolösa kubiska plana grafer. I en Hamiltonsk kubisk plan graf är en sådan kantfärgning lätt att hitta: använd två färger omväxlande på cykeln och en tredje färg för alla återstående kanter. Alternativt kan en 4-färgning av ytorna på en Hamiltonsk kubisk plan graf konstrueras direkt, med två färger för ytorna inuti cykeln och ytterligare två färger för ytorna utanför.
Tuttes motexempel
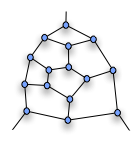
Tuttes fragment
Nyckeln till detta motexempel är det som nu kallas Tuttes fragment , som visas till höger.
Om det här fragmentet är en del av en större graf, måste varje Hamilton-cykel genom grafen gå in eller ut ur den översta vertexen (och antingen en av de lägre). Den kan inte gå in i ena nedre hörn och ut i den andra.
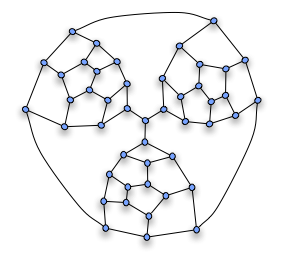
Motexemplet
Fragmentet kan sedan användas för att konstruera den icke-Hamiltonska Tutte-grafen genom att sätta ihop tre sådana fragment som visas på bilden. De "obligatoriska" kanterna på fragmenten, som måste vara en del av någon Hamiltonsk väg genom fragmentet, är anslutna vid den centrala vertexen; eftersom varje cykel bara kan använda två av dessa tre kanter, kan det inte finnas någon Hamilton-cykel.
Den resulterande Tutte-grafen är 3-kopplad och plan , så enligt Steinitz sats är det grafen för en polyeder. Totalt har den 25 ytor, 69 kanter och 46 hörn. Det kan realiseras geometriskt från en tetraeder (vars ytor motsvarar de fyra stora ytorna på ritningen, varav tre är mellan par av fragment och den fjärde utgör exteriören) genom att multiplicera avkortning av tre av dess hörn.
Mindre motexempel
Som Holton & McKay (1988) visar, finns det exakt sex 38-vertex icke-Hamiltonska polyedrar som har icke-triviala trekantssnitt. De bildas genom att ersätta två av hörnen på ett femkantigt prisma med samma fragment som används i Tuttes exempel.
Se även
- Grinbergs sats , ett nödvändigt villkor för förekomsten av en Hamiltonsk cykel som kan användas för att visa att en graf utgör ett motexempel till Taits gissning
- Barnettes gissning , en fortfarande öppen förfining av Taits gissning som säger att varje tvådelad kubisk polyedrisk graf är Hamiltonsk.
Anteckningar
- Holton, DA; McKay, BD (1988), "De minsta icke-Hamiltonska 3-anslutna kubiska plana graferna har 38 hörn", Journal of Combinatorial Theory, Series B , 45 (3): 305–319, doi : 10.1016/0095-8956(8888) )90075-5 .
- Tait, PG (1884), "Listing's Topologie ", Philosophical Magazine , 5:e serien, 17 : 30–46 . Omtryckt i Scientific Papers , Vol. II, s. 85–98.
- Tutte, WT (1946), "On Hamiltonian circuits" (PDF) , Journal of the London Mathematical Society , 21 (2): 98–101, doi : 10.1112/jlms/s1-21.2.98 .
Delvis baserat på sci.math-inlägg av Bill Taylor , använt med tillstånd.