Vinkelmomentdiagram (kvantmekanik)

Inom kvantmekaniken och dess tillämpningar på kvantmångpartikelsystem , särskilt kvantkemi , är rörelsemängdsdiagram , eller mer exakt från en matematisk synvinkel rörelsemängdsgrafer, en schematisk metod för att representera rörelsemängdskvanttillstånd i ett kvantsystem som tillåter beräkningar gjort symboliskt. Mer specifikt kodar pilarna vinkelmomenttillstånd i bra–ket-notation och inkluderar tillståndets abstrakta natur, såsom tensorprodukter och transformationsregler.

Notationen liknar idén med Penrose grafisk notation och Feynman diagram . Diagrammen består av pilar och hörn med kvantnummer som etiketter, därav den alternativa termen " grafer ". Avkänningen av varje pil är relaterad till hermitisk konjugation , som ungefär motsvarar tidsomkastning av rörelsemängdstillstånden (jfr Schrödinger-ekvationen ) . Den schematiska notationen är ett avsevärt stort ämne i sin egen rätt med ett antal specialiserade funktioner – den här artikeln introducerar grunderna.

De utvecklades främst av Adolfas Jucys (ibland översatt som Yutsis) på 1900-talet.

Ekvivalens mellan Dirac-notation och Jucys-diagram

Vinkelmoment tillstånd

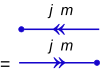
Kvanttillståndsvektorn för en enskild partikel med totalt vinkelmoment kvanttal j och totalt magnetiskt kvanttal m = j , j − 1, ..., − j + 1, − j , betecknas som en ket | j , m ⟩ . Som ett diagram är detta en pil med en huvud.

Symmetriskt är motsvarande behå ⟨ j , m | . I diagramform är detta en två huvuden som pekar i motsatt riktning mot keten.

I varje fall;

• kvanttalen j , m är ofta märkta bredvid pilarna för att referera till ett specifikt rörelsemängdstillstånd,
• pilspetsar är nästan alltid placerade i mitten av linjen, snarare än vid spetsen,
• likhetstecken "=" placeras mellan ekvivalenta diagram, precis som för flera algebraiska uttryck lika med varandra.

De mest grundläggande diagrammen är för kettor och behåar:

Ket | j , m ⟩

BH ⟨ j , m |

Pilar riktas till eller från hörn, ett tillstånd som transformeras enligt:

• en standardrepresentation betecknas med en orienterad linje som lämnar en vertex,
• en kontrastandardisk representation avbildas som en linje som går in i en vertex.

Som en allmän regel följer pilarna varandra i samma mening. I den kontrastandardiserade representationen används tidsomkastningsoperatorn , här betecknad med T . Den är enhetlig, vilket betyder att det hermitiska konjugatet T ^† är lika med den inversa operatorn T ⁻¹ , det vill säga T ^† = T ⁻¹ . Dess verkan på positionsoperatören lämnar den oföränderlig:

$T{\hat {\mathbf {x} }}T^{\dolk }={\hat {\mathbf {x} }}$

men den linjära momentumoperatorn blir negativ:

$T{\hat {\mathbf {p} }}T^{\dolk }=-{\hat {\mathbf {p} }}$

och spinnoperatorn blir negativ:

$T{\hat {\mathbf {S} }}T^{\dolk }=-{\hat {\mathbf {S} }}$

Eftersom den orbitala rörelsemängdsoperatorn är L = x × p måste denna också bli negativ:

$T{\hat {\mathbf {L} }}T^{\dolk }=-{\hat {\mathbf {L} }}$

och därför blir den totala rörelsemängdsoperatorn J = L + S negativ:

$T{\hat {\mathbf {J} }}T^{\dolk }=-{\hat {\mathbf {J} }}$

Verkar på ett egentillstånd av rörelsemängd | j , m ⟩ , det kan visas att:

$T\left|j,m\right\rangle \equiv \left|T(j,m)\right\rangle ={(-1)}^{jm}\left|j, -m\right\rangle$

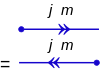
De omvända diagrammen för kettor och behåar är:

Tid omvänt ket | j , m ⟩ .

Tid omvänd bh ⟨ j , m | .

Det är viktigt att positionera vertexet korrekt, eftersom operatörer för fram- och omvänd tid skulle blandas ihop.

Inre produkt

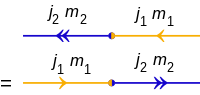
Den inre produkten av två tillstånd | j ₁ , m ₁ ⟩ och | j ₂ , m ₂ ⟩ är:

$\langle j_{2},m_{2}|j_{1},m_{1}\rangle =\delta _{j_{ 1}j_{2}}\delta _{m_{1}m_{2}}$

och diagrammen är:

Inre produkt av | j ₁ , m ₁ ⟩ och | j ₂ , m ₂ ⟩ , det vill säga ⟨ j ₂ , m ₂ | j ₁ , m ₁ ⟩ .

Tid omvänt ekvivalent.

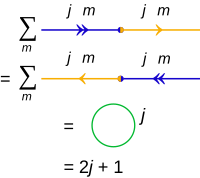
För summeringar över den inre produkten, även känd i detta sammanhang som en kontraktion (jfr tensorkontraktion) :

$\sum _{m}\langle j,m|j,m\rangle =2j+1$

det är vanligt att beteckna resultatet som en sluten cirkel endast märkt med j , inte m :

Inre produktsammandragning.

Yttre produkter

Den yttre produkten av två tillstånd | j ₁ , m ₁ ⟩ och | j ₂ , m ₂ ⟩ är en operator:

$\left|j_{2},m_{2}\right\rangle \left\langle j_{1},m_{1}\right|$

och diagrammen är:

Yttre produkt av | j ₁ , m ₁ ⟩ och | j ₂ , m ₂ ⟩ , det vill säga | j ₂ , m ₂ ⟩ ⟨ j ₁ , m ₁ | .

Tid omvänt ekvivalent.

För summeringar över den yttre produkten, även känd i detta sammanhang som en kontraktion (jfr tensorkontraktion) :

${\begin{aligned}\sum _{m}|j,m\rangle \langle j,m|&=\summa _{m}|j,-m\rangle \langle j,-m |\\&=\summa _{m}{(-1)}^{2(jm)}|j,-m\rangle \langle j,-m|\\&=\summa _{m}{( -1)}^{jm}|j,-m\rangle \langle j,-m|{(-1)}^{jm}\\&=\summa _{m}T|j,m\rangle \ lange j,m|T^{\dolk }\end{aligned}}$

där resultatet för T | j , m ⟩ användes, och det faktum att m tar uppsättningen av värden som anges ovan. Det finns ingen skillnad mellan tillstånden framåt och omvänd tid för den yttre produktkontraktionen, så här delar de samma diagram, representerat som en linje utan riktning, återigen märkt med endast j och inte m :

Yttre produktsammandragning.

Tensor produkter

Tensorprodukten ⊗ av n tillstånd | j ₁ , m ₁ ⟩ , | j ₂ , m ₂ ⟩ , ... | j _n , m _n ⟩ skrivs

${\begin{aligned}\left|j_{1},m_{1},j_{2},m_{2},...j_{n},m_{n} \right\rangle &\equiv \left|j_{1},m_{1}\right\rangle \otimes \left|j_{2},m_{2}\right\rangle \otimes \cdots \otimes \left| j_{n},m_{n}\right\rangle \\&\equiv \left|j_{1},m_{1}\right\rangle \left|j_{2},m_{2}\right\rangle \cdots \left|j_{n},m_{n}\right\rangle \end{aligned}}$

och i diagramform lämnar eller går varje separat tillstånd in i en gemensam vertex och skapar en "fan" av pilar - n linjer fästa vid en enda vertex.

Vertices i tensorprodukter har tecken (ibland kallade "nodtecken"), för att indikera ordningen för de tensormultiplicerade tillstånden:

• ett minustecken (−) anger att ordningen är medurs , $circlearrowright }$ \ , och
• ett plustecken (+) för moturs , $\displaystyle \circlearrowleft }$ { .

Skyltar krävs naturligtvis inte för bara ett tillstånd, schematiskt en pil vid en vertex. Ibland ingår böjda pilar med tecknen för att explicit visa känslan av tensormultiplikation, men vanligtvis visas bara tecknet med pilarna utelämnade.

Tensorprodukt av | j ₁ , m ₁ ⟩ , | j ₂ , m ₂ ⟩ , | j ₃ , m ₃ ⟩ , det vill säga | j ₁ , m ₁ ⟩ | j ₂ , m ₂ ⟩ | j ₃ , m ₃ ⟩ = | j ₁ , m ₁ , j ₂ , m ₂ , j ₃ , m ₃ ⟩ . På samma sätt för mer än tre vinkelmoment.

Tid omvänt ekvivalent.

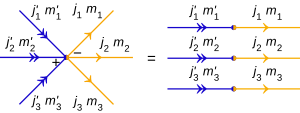
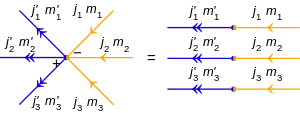
För den inre produkten av två tensorprodukttillstånd:

${\begin{aligned}&\left\langle j'_{n},m'_{n},...,j'_{2},m'_{2 },j'_{1},m'_{1}|j_{1},m_{1},j_{2},m_{2},...j_{n},m_{n}\right \rangle \\=&\langle j'_{n},m'_{n}|...\langle j'_{2},m'_{2}|\langle j'_{1}, m'_{1}||j_{1},m_{1}\rangle |j_{2},m_{2}\rangle ...|j_{n},m_{n}\rangle \\=& \prod _{k=1}^{n}\left\langle j'_{k},m'_{k}|j_{k},m_{k}\right\rangle \end{aligned}}$

det finns n massor av inre produktpilar:

Inre produkt av | j′1 , m′1 , j′2 , m′2 , j′3 _{, m′3⟩ och} | _ _{_} _ _ _ _{_} _ _ _ _{_} _ _ _ j ₁ , m ₁ , j ₂ , m ₂ , j ₃ , m ₃ ⟩ , _det säga ⟨ j ′ ₃ , m ′ ₃ , j 2 , m ₂ , j ₁ , m ₁ | _ j ₁ , m ₁ , j ₂ , m ₂ , j ₃ , m ₃ ⟩ vill . På samma sätt för mer än tre par vinkelmoment.

Tid omvänt ekvivalent.

Exempel och tillämpningar

• Diagrammen är väl lämpade för Clebsch–Gordan-koefficienter .
• Beräkningar med verkliga kvantsystem, såsom multielektronatomer och molekylära system.

Diagram för en 6-j symbol , ${\begin{Bmatrix}j_{1}&j_{2}&j_{3}\\j_{4}&j_ {5}&j_{6}\end{Bmatrix}}$ .

Diagram för en 9-j symbol , ${\begin{Bmatrix}j_{1}&j_{2}&j_{3}\ \j_{4}&j_{5}&j_{6}\\j_{7}&j_{8}&j_{9}\end{Bmatrix}}$ .

Se även

• Vektormodell av atomen
• Stegeoperatör
• Fock utrymme
• Feynman-diagram

• Yutsis, Adolfas P.; Levinson, IB; Vanagas, VV (1962). Matematisk apparat för teorin om rörelsemängd . Översatt av A. Sen; RN Sen. Israel Program för vetenskapliga översättningar.
• Wormer och Paldus (2006) ger en djupgående handledning i vinkelmomentdiagram.
•   I. Lindgren; J. Morrison (1986). Atomisk många kroppsteori . Kemisk fysik. Vol. 13 (andra upplagan). Springer-Verlag. ISBN 978-3-540-16649-8 .

Vidare läsning

•   GWF Drake (2006). Springer Handbook of Atomic, Molecular, and Optical Physics (2nd ed.). springer. sid. 60. ISBN 978-0-387-26308-3 .
•   U. Kaldor; S. Wilson (2003). Teoretisk kemi och fysik för tunga och supertunga grundämnen . Framsteg i teoretisk kemi och fysik. Vol. 11. springer. sid. 183. ISBN 978-1-4020-1371-3 .
•   EJ Brändas; PO Löwdin; E. Brändas; ES Kryachko (2004). Grundläggande värld av kvantkemi: En hyllning till minnet av Per-Olov Löwdin . Vol. 3. Springer. sid. 385. ISBN 978-1-4020-2583-9 .
•   P. Schwerdtfeger (2004). Relativistisk elektronisk strukturteori: Del 2. Tillämpningar . Teoretisk och beräkningskemi. Vol. 14. Elsevier. sid. 97. ISBN 978-0-08-054047-4 .
•   M. Barysz; Y. Ishikawa (2010). Relativistiska metoder för kemister . Utmaningar och framsteg inom beräkningskemi och fysik. Vol. 10. Springer. sid. 311. ISBN 978-1-4020-9975-5 .

•   GHF Diercksen; S. Wilson (1983). Metoder i beräkningsmolekylär fysik . NATO Science Series C. Vol. 113. Springer. ISBN 978-90-277-1638-5 .
•   Zenonas Rudzikas (2007). "8" . Teoretisk atomspektroskopi . Cambridge Monographs on Atomic, Molecular and Chemical Physics. Vol. 7. University of Chicago: Cambridge University Press. ISBN 978-0-521-02622-2 .
• Lietuvos Fizikų draugija (2004). Lietuvos fizikos žurnalas . Vol. 44. University of Chicago: Draugija.
•   PET Jorgensen (1987). Operatörs- och representationsteori: kanoniska modeller för algebror av operatörer som uppstår i kvantmekanik . University of Chicago: Elsevier. ISBN 978-0-08-087258-2 .
•   P. Cvitanović (2008). Gruppteori - Fågelspår, lögner och exceptionella grupper . Princeton, NJ: Princeton Univ. Tryck. ISBN 978-0-691-11836-9 .