Euklidisk plan isometri

I geometri är en euklidisk plan isometri en isometri av det euklidiska planet , eller mer informellt, ett sätt att omvandla planet som bevarar geometriska egenskaper som längd. Det finns fyra typer: translationer , rotationer , reflektioner och glidreflektioner (se nedan under Klassificering § Notes ) .

Uppsättningen av euklidiska planisometrier bildar en grupp under sammansättning : den euklidiska gruppen i två dimensioner. Den genereras av reflektioner i linjer, och varje element i den euklidiska gruppen är sammansatt av högst tre distinkta reflektioner.

Informell diskussion

Informellt är en euklidisk plan isometri något sätt att transformera planet utan att "deformera" det. Anta till exempel att det euklidiska planet representeras av ett ark av genomskinlig plast som sitter på ett skrivbord. Exempel på isometrier inkluderar:

Flytta arket en tum åt höger.
Rotera arket tio grader runt en markerad punkt (som förblir orörlig).
Vänd på lakanet för att titta på det bakifrån. Lägg märke till att om en bild ritas på ena sidan av arket, ser vi spegelbilden av bilden efter att ha vänt arket.

Det här är exempel på översättningar , rotationer respektive reflektioner . Det finns ytterligare en typ av isometri, som kallas glidreflektion (se nedan under klassificering av euklidiska planisometrier ).

Vikning, skärning eller smältning av arket anses dock inte vara isometrier. Det är inte heller mindre drastiska förändringar som böjning, sträckning eller vridning.

Formell definition

En isometri av det euklidiska planet är en avståndsbevarande transformation av planet. Det vill säga, det är en karta

M:{\textbf {R}}^{2}\to {\textbf {R}}^{2}

så att för alla punkter p och q i planet,

d(p,q)=d(M(p),M(q)),

där d ( p , q ) är det vanliga euklidiska avståndet mellan p och q .

Klassificering

Det kan visas att det finns fyra typer av euklidiska planisometrier. ( Obs : beteckningarna för de typer av isometrier som anges nedan är inte helt standardiserade.)

Reflektioner

Reflexion

Reflektioner , eller spegelisometrier , betecknade med F _{c , v} , där c är en punkt i planet och v är en enhetsvektor i R ² . ( F är för "vända".) har effekten att reflektera punkten p på linjen L som är vinkelrät mot v och som går genom c . Linjen L kallas reflektionsaxeln eller tillhörande spegel . För att hitta en formel för F _{c , v} , använder vi först punktprodukten för att hitta komponenten t av p − c i v -riktningen,

t=(pc)\cdot v=(p_{x}-c_{ x})v_{x}+(p_{y}-c_{y})v_{y},

och sedan får vi reflektionen av p genom subtraktion,

F_{c,v}(p)=p-2tv.

Kombinationen av rotationer kring origo och reflektioner kring en linje genom origo erhålls med alla ortogonala matriser (dvs med determinant 1 och −1) som bildar ortogonal grupp O (2). I fallet med en determinant på −1 har vi:

R_{0,\theta }(p)={\begin{bmatrix}\cos \theta &\sin \theta \\\sin \theta &\mathbf {-} \cos \theta \end{bmatrix} }{\begin{bmatrix}p_{x}\\p_{y}\end{bmatrix}}.

som är en reflektion i x -axeln följt av en rotation med en vinkel θ , eller ekvivalent, en reflektion i en linje som bildar en vinkel på θ /2 med x -axeln. Reflektion i en parallell linje motsvarar att lägga till en vektor vinkelrät mot den.

Översättningar

Översättning

Översättningar , betecknade med T _v , där v är en vektor i R ² har effekten att förskjuta planet i riktning mot v . Det vill säga för vilken punkt p som helst i planet,

T_{v}(p)=p+v,

eller i termer av ( x , y ) koordinater,

T_{v}(p)={\begin{bmatrix}p_{x}+v_{x}\\p_{y}+v_{y}\end{bmatrix}}.

En translation kan ses som en sammansättning av två parallella reflektioner.

Rotationer

Rotation

Rotationer , betecknade med R _c,θ , där c är en punkt i planet (rotationscentrum), och θ är rotationsvinkeln. I termer av koordinater uttrycks rotationer enklast genom att dela upp dem i två operationer. Först ges en rotation runt origo av

R_{0,\theta }(p)={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}{\begin {bmatrix}p_{x}\\p_{y}\end{bmatrix}}.

Dessa matriser är de ortogonala matriserna (dvs var och en är en kvadratisk matris G vars transponering är dess invers , dvs $GG^{T}=G^{T}G=I_{ 2}.$ ), med determinant 1 (den andra möjligheten för ortogonala matriser är −1, vilket ger en spegelbild, se nedan). De bildar den speciella ortogonala gruppen SO(2).

En rotation runt c kan åstadkommas genom att först översätta c till origo, sedan utföra rotationen runt origo och slutligen översätta origo tillbaka till c . Det är,

R_{c,\theta }=T_{c}\circ R_{0,\theta }\circ T_{-c},

eller med andra ord,

R_{c,\theta }(p)=c+R_{0,\theta }(st).

Alternativt utförs en rotation runt origo, följt av en translation:

R_{c,\theta }(p)=c-R_{0,\theta}c+R_{0,\theta }(p).

En rotation kan ses som en sammansättning av två icke-parallella reflektioner.

Stela transformationer

Uppsättningen av translationer och rotationer bildar tillsammans de stela rörelserna eller stela förskjutningarna . Denna uppsättning bildar en grupp under sammansättning, gruppen av stela rörelser , en undergrupp av hela gruppen av euklidiska isometrier.

Glidreflektioner

Glidreflektion

Glidreflektioner , betecknade med G _{c , v , w} , där c är en punkt i planet, v är en enhetsvektor i R ² och w är icke-null en vektor vinkelrät mot v är en kombination av en reflektion i linjen beskrivs av c och v följt av en översättning längs w . Det är,

G_{c,v,w}=T_{w}\circ F_{c,v},

eller med andra ord,

G_{c,v,w}(p)=w+F_{c,v}(p).

(Det är också sant att

G_{c,v,w}(p)=F_{c,v}(p+w);

det vill säga vi får samma resultat om vi gör översättningen och reflektionen i motsatt ordning.)

Alternativt multiplicerar vi med en ortogonal matris med determinant −1 (motsvarande en reflektion i en linje genom origo), följt av en translation. Detta är en glidreflektion, förutom i det speciella fallet att translationen är vinkelrät mot reflektionslinjen, i vilket fall kombinationen i sig bara är en reflektion i en parallell linje.

Identitetsisometrin , definierad av I ( p ) = p för alla punkter p är ett specialfall av en translation, och även ett specialfall av en rotation . Det är den enda isometrin som tillhör mer än en av de ovan beskrivna typerna.

I alla fall multiplicerar vi positionsvektorn med en ortogonal matris och adderar en vektor; om determinanten är 1 har vi en rotation, en translation eller identiteten, och om den är −1 har vi en glidreflektion eller en reflektion.

En "slumpmässig" isometri, som att ta ett pappersark från ett bord och slumpmässigt lägga tillbaka det, är " nästan säkert " en rotation eller en glidreflektion (de har tre frihetsgrader ). Detta gäller oavsett detaljerna i sannolikhetsfördelningen , så länge som θ och riktningen för den adderade vektorn är oberoende och likformigt fördelade och längden på den adderade vektorn har en kontinuerlig fördelning. En ren översättning och en ren reflektion är specialfall med endast två frihetsgrader, medan identiteten är ännu mer speciell, utan frihetsgrader.

Isometrier som reflektionsgrupp

Reflektioner, eller spegelisometrier, kan kombineras för att producera vilken isometri som helst. Sålunda är isometrier ett exempel på en reflektionsgrupp .

Spegelkombinationer

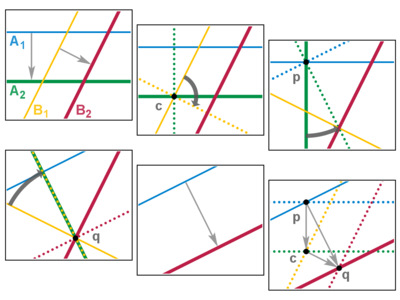
På det euklidiska planet har vi följande möjligheter.

[ d ] Identitet

Två reflektioner i samma spegel återställer varje punkt till sin ursprungliga position. Alla punkter är kvar fixerade. Alla par identiska speglar har samma effekt.

[ d b ] Reflektion

När Alice hittade genom spegeln , får en enda spegel vänster och höger hand att byta. (I formella termer är topologisk orientering omvänd.) Punkter på spegeln lämnas fixerade. Varje spegel har en unik effekt.

[ d p ] Rotation

Två distinkta skärande speglar har en gemensam punkt som förblir fixerad. Alla andra punkter roterar runt den med två gånger vinkeln mellan speglarna. Alla två speglar med samma fixpunkt och samma vinkel ger samma rotation, så länge de används i rätt ordning.

[ d d ] Translation

Två distinkta speglar som inte skär varandra måste vara parallella. Varje punkt rör sig lika mycket, två gånger avståndet mellan speglarna och i samma riktning. Inga punkter lämnas fasta. Alla två speglar med samma parallella riktning och samma avstånd från varandra ger samma översättning, så länge de används i rätt ordning.

[ d q ] Glidreflektion

Tre speglar. Om de alla är parallella är effekten densamma som en enkel spegel (skjut ett par för att avbryta det tredje). Annars kan vi hitta ett ekvivalent arrangemang där två är parallella och den tredje är vinkelrät mot dem. Effekten är en reflektion kombinerad med en translation parallellt med spegeln. Inga punkter lämnas fasta.

Tre speglar räcker

Att lägga till fler speglar ger inte fler möjligheter (i planet), eftersom de alltid kan arrangeras om för att orsaka avbokning.

Bevis

En isometri bestäms helt av dess effekt på tre oberoende (inte kolinjära) punkter. Så antag att p ₁ , p ₂ , p ₃ mappar till q ₁ , q ₂ , q ₃ ; vi kan generera en sekvens av speglar för att uppnå detta enligt följande. Om p ₁ och q ₁ är distinkta, välj deras vinkelräta bisektris som spegel. Nu mappar p _{1 till} q ₁ ; och vi kommer att passera alla ytterligare speglar genom q ₁ och lämnar den fixerad. Kalla bilderna av p ₂ och p ₃ under denna reflektion p ₂ ′ och p ₃ ′. Om q ₂ är skild från p ₂ ′, dela vinkeln vid q ₁ med en ny spegel. Med p ₁ och p ₂ nu på plats, är p _{3 på} p ₃ ″; och om den inte är på plats kommer en sista spegel genom q ₁ och q ₂ att vända den till q ₃ . Således räcker högst tre reflektioner för att reproducera vilken plan isometri som helst. QED

Erkännande

Vi kan känna igen vilka av dessa isometrier vi har beroende på om den bevarar händer eller byter dem, och om den har minst en fast punkt eller inte, som visas i följande tabell (utan identiteten).

		Bevarar händerna?
		Ja	Nej
Fixpunkt?	Ja	Rotation	Reflexion
Fixpunkt?	Nej	Översättning	Glidreflektion

Gruppstruktur

Isometrier som kräver ett udda antal speglar – reflektion och glidreflektion – vänder alltid åt vänster och höger. De jämna isometrierna – identitet, rotation och translation – gör det aldrig; de motsvarar stela rörelser och bildar en normal undergrupp av den fullständiga euklidiska gruppen av isometrier. Varken hela gruppen eller den jämna undergruppen är abelska ; till exempel, omvänd ordning av sammansättningen av två parallella speglar omvänder riktningen för översättningen de producerar.

Bevis

Identiteten är en isometri; ingenting förändras, så avståndet kan inte ändras. Och om en isometri inte kan ändra avståndet, så kan inte två (eller tre eller fler) i följd heller; sålunda är sammansättningen av två isometrier återigen en isometri, och uppsättningen av isometrier är sluten under sammansättning. Identitetsisometrin är också en identitet för sammansättning, och sammansättning är associativ ; därför uppfyller isometrier axiomen för en halvgrupp . För en grupp måste vi också ha en invers för varje element. För att avbryta en reflektion komponerar vi den bara med sig själv (Reflections are involutions ). Och eftersom varje isometri kan uttryckas som en sekvens av reflektioner, kan dess invers uttryckas som den sekvensen omvänd. Lägg märke till att annulleringen av ett par identiska reflektioner minskar antalet reflektioner med ett jämnt tal, vilket bevarar sekvensens paritet; märk också att identiteten har jämn paritet. Därför bildar alla isometrier en grupp, och även isometrier en undergrupp. (Uda isometrier inkluderar inte identiteten, så är inte en undergrupp). Denna undergrupp är en normal undergrupp, eftersom att lägga en jämn isometri mellan två udda ger en jämn isometri. QED

Eftersom den jämna undergruppen är normal är den kärnan i en homomorfism till en kvotgrupp , där kvoten är isomorf till en grupp som består av en reflektion och identiteten. Hela gruppen är dock inte en direkt produkt utan bara en halvdirekt produkt av den jämna undergruppen och kvotgruppen.

Sammansättning

Sammansättningen av isometrier blandar sorter på olika sätt. Vi kan tänka på identiteten som antingen två speglar eller ingen; hur som helst, det har ingen effekt i sammansättningen. Och två reflektioner ger antingen en translation eller en rotation, eller identiteten (vilket är båda, på ett trivialt sätt). Reflektion sammansatt med endera av dessa kan upphäva ner till en enda reflektion; annars ger den den enda tillgängliga isometrin med tre spegel, en glidreflektion. Ett par översättningar reduceras alltid till en enda översättning; så de utmanande fallen involverar rotationer. Vi vet att en rotation som består av antingen en rotation eller en translation måste producera en jämn isometri. Komposition med translation ger en annan rotation (med samma mängd, med förskjuten fixpunkt), men komposition med rotation kan ge antingen translation eller rotation. Det sägs ofta att sammansättning av två rotationer ger en rotation, och Euler bevisade en sats om detta i 3D; detta gäller dock endast för rotationer som delar en fast punkt.

Translation, rotation och ortogonala undergrupper

Vi har alltså två nya typer av isometriundergrupper: alla translationer och rotationer som delar en fast punkt. Båda är undergrupper till den jämna undergruppen, inom vilka översättningar är normala. Eftersom översättningar är en normal undergrupp, kan vi räkna bort dem och lämna undergruppen av isometrier med en fast punkt, den ortogonala gruppen .

Bevis

Om två rotationer delar en fast punkt, kan vi svänga spegelparet i den andra rotationen för att avbryta de inre speglarna i sekvensen av fyra (två och två), och bara lämna det yttre paret. Sammansättningen av två rotationer med en gemensam fixpunkt ger alltså en rotation med summan av vinklarna kring samma fixpunkt.

Om två translationer är parallella kan vi skjuta spegelparet i den andra translationen för att avbryta den inre spegeln i sekvensen av fyra, ungefär som i rotationsfallet. Sammansättningen av två parallella översättningar ger alltså en translation med summan av avstånden i samma riktning. Antag nu att översättningarna inte är parallella och att spegelsekvensen är A ₁ , A ₂ (den första översättningen) följt av B ₁ , B ₂ (den andra). Då måste A ₂ och B ₁ korsa, säg vid c ; och genom att återassociera är vi fria att svänga detta inre par runt c . Om vi svänger 90° händer en intressant sak: nu skär A ₁ och A ₂ ′ i en 90° vinkel, säg vid p , och det gör B ₁ ′ och B ₂ , säg vid q . Återigen associerar vi det första paret runt p för att få B ₂ ″ att passera genom q , och svänger det andra paret runt q för att få A ₁ ″ att passera genom p . De inre speglarna sammanfaller nu och upphäver, och de yttre speglarna lämnas parallella. Sammansättningen av två icke-parallella översättningar ger alltså också en översättning. Dessutom bildar de tre vridpunkterna en triangel vars kanter ger huvud-till-svans-regeln för $vektoraddition : p c) + 2(cq) = 2(pq)$ 2 ( . QED

Kapslad gruppkonstruktion

Undergruppsstrukturen föreslår ett annat sätt att komponera en godtycklig isometri:

Välj en fast punkt och en spegel genom den.

Om isometrin är udda, använd spegeln; annars inte.
Vid behov, rotera runt den fasta punkten.
Om det behövs, översätt.

Detta fungerar eftersom översättningar är en normal undergrupp av hela gruppen av isometrier, med kvoten den ortogonala gruppen; och rotationer kring en fast punkt är en normal undergrupp av den ortogonala gruppen, med kvoten en enda reflektion.

Diskreta undergrupper

De undergrupper som diskuterats hittills är inte bara oändliga, de är också kontinuerliga ( Lie-grupper) . Varje undergrupp som innehåller minst en översättning som inte är noll måste vara oändlig, men undergrupper av den ortogonala gruppen kan vara ändliga. Till exempel symmetrierna för en vanlig femhörning av rotationer med heltalsmultiplar på 72° (360° / 5), tillsammans med reflektioner i de fem speglarna som delar kanterna vinkelrätt. Detta är en grupp, D ₅ , med 10 element. Den har en undergrupp, C ₅ , av halva storleken, utan reflektionerna. Dessa två grupper är medlemmar av två familjer, D _n och C _n , för varje n > 1. Tillsammans utgör dessa familjer rosettgrupperna .

Översättningar viker sig inte tillbaka på sig själva, men vi kan ta heltalsmultiplar av vilken finit översättning som helst, eller summor av multipler av två sådana oberoende översättningar, som en undergrupp. Dessa genererar gittret av en periodisk plattsättning av planet.

Vi kan också kombinera dessa två typer av diskreta grupper - de diskreta rotationerna och reflektionerna runt en fast punkt och de diskreta translationerna - för att generera frisgrupperna och tapetgrupperna . Märkligt nog visar sig bara ett fåtal av fixpunktsgrupperna vara kompatibla med diskreta översättningar. Faktum är att gitterkompatibilitet innebär en så allvarlig begränsning att vi, upp till isomorfism , bara har 7 distinkta frisgrupper och 17 distinkta tapetgrupper. Till exempel är pentagonsymmetrierna, D5 _, inkompatibla med ett diskret gitter av translationer. (Varje högre dimension har också bara ett ändligt antal sådana kristallografiska grupper , men antalet växer snabbt; till exempel har 3D 230 grupper och 4D har 4783.)

Isometrier i det komplexa planet

När det gäller komplexa tal är planets isometrier antingen av formen

{\begin{array}{ccc}\mathbb {C} &\longrightarrow &\mathbb {C} \\z&\mapsto &a+\omega z\end{array}}

eller av formen

{\begin{array}{ccc}\mathbb {C} &\longrightarrow &\mathbb {C} \\z&\mapsto &a+\omega {\overline {z }}{\mbox{,}}\end{array}}

för vissa komplexa tal $a$ och $ω$ med |ω| = 1. Detta är lätt att bevisa: om $a = f (0)$ och $ω = f (1) - f (0)$ och om man definierar

{\begin{array}{rccc}g\colon &\mathbb {C} &\longrightarrow &\mathbb {C} \\&z&\mapsto &{\frac {f(z)-a}{\omega }}{\mbox{,}}\end{array}}

då är $g$ en isometri, $g (0) = 0$ , och $g (1) = 1$ . Det är då lätt att se att g antingen är identiteten eller konjugationen, och påståendet som bevisas följer av detta och av att $f (z) = a + ωg (z)$ .

Detta är uppenbarligen relaterat till den tidigare klassificeringen av planisometrier, eftersom:

funktioner av typen $z \to a + z$ är översättningar;
funktioner av typen $z \to ω z$ är rotationer (när |ω| = 1);
konjugationen är en reflektion.

Observera att en rotation kring komplex punkt p erhålls genom komplex aritmetik med

z\mapsto \omega (zp)+p=\omega z+p(1-\omega )

där det sista uttrycket visar mappningen som motsvarar rotation vid 0 och en translation. Därför, givet direkt isometri $z\mapsto \omega z+a,$ kan man lösa $p(1-\omega )=a$ till erhåll $p=a/(1-\omega )$ som centrum för en ekvivalent rotation, förutsatt att $\omega \neq 1$ , dvs. förutsatt att den direkta isometrin inte är en ren översättning. Som sagt av Cederberg, "En direkt isometri är antingen en rotation eller en translation."

Se även

Beckman–Quarles teorem , en karakterisering av isometrier som de transformationer som bevarar enhetsavstånd
Kongruens (geometri)
Koordinera rotationer och reflektioner
Hjelmslevs teorem , påståendet att mittpunkterna för motsvarande par av punkter i en isometri av linjer är kolinjära

externa länkar

Plan isometrier