Kärnfusion

 |
| Kärnfysik |
|---|
| Kärna · Nukleoner ( p , n ) · Kärnämne · Kärnkraft · Kärnstruktur · Kärnreaktion |
Kärnfusion är en reaktion där två eller flera atomkärnor kombineras för att bilda en eller flera olika atomkärnor och subatomära partiklar ( neutroner eller protoner ). Skillnaden i massa mellan reaktanterna och produkterna visar sig antingen som frigöring eller absorption av energi . Denna skillnad i massa uppstår på grund av skillnaden i kärnbindningsenergi mellan atomkärnorna före och efter reaktionen. Kärnfusion är den process som driver aktiva stjärnor eller huvudsekvensstjärnor och andra stjärnor med hög magnitud , där stora mängder energi frigörs .
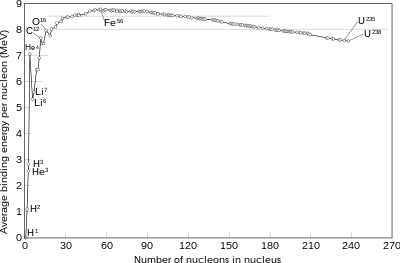
En kärnfusionsprocess som producerar atomkärnor lättare än järn-56 eller nickel-62 kommer i allmänhet att frigöra energi. Dessa grundämnen har en relativt liten massa och en relativt stor bindningsenergi per nukleon . Fusion av kärnor som är lättare än dessa frigör energi (en exoterm process), medan sammansmältningen av tyngre kärnor resulterar i energi som kvarhålls av produktnukleonerna, och den resulterande reaktionen är endoterm . Motsatsen är sant för den omvända processen, kallad kärnklyvning . Kärnfusion använder lättare grundämnen, såsom väte och helium , som i allmänhet är mer smältbara; medan de tyngre grundämnena, såsom uran , thorium och plutonium , är mer klyvbara. Den extrema astrofysiska händelsen av en supernova kan producera tillräckligt med energi för att smälta samman kärnor till element som är tyngre än järn.
Historia
År 1920 föreslog Arthur Eddington att väte-heliumfusion kunde vara den primära källan till stjärnenergi. Kvanttunneling upptäcktes av Friedrich Hund 1927, och kort därefter använde Robert Atkinson och Fritz Houtermans de uppmätta massorna av lätta element för att visa att stora mängder energi kunde frigöras genom att smälta samman små kärnor. Byggande på de tidiga experimenten i artificiell kärntransmutation av Patrick Blackett , genomfördes laboratoriefusion av väteisotoper av Mark Oliphant 1932. Under resten av det decenniet utarbetades teorin om huvudcykeln för kärnfusion i stjärnor av Hans Bethe . Forskning om fusion för militära ändamål började i början av 1940-talet som en del av Manhattan Project . Självförsörjande kärnfusion genomfördes första gången den 1 november 1952, i Ivy Mike väte (termonukleär) bombtest.
Även om fusion uppnåddes i driften av vätebomben (H-bomben), för att den ska vara en användbar energikälla, krävs en ihållande fusion. Forskning om att utveckla kontrollerad fusion inuti fusionsreaktorer har pågått sedan 1930-talet, men tekniken är fortfarande i sin utvecklingsfas.
US National Ignition Facility , som använder laserdriven tröghetsinneslutningsfusion , designades med ett mål om break-even fusion; de första storskaliga lasermålexperimenten utfördes i juni 2009 och antändningsexperiment påbörjades i början av 2011. Den 13 december 2022 USA:s energidepartement att de den 5 december 2022 framgångsrikt hade uppnått break-even fusion, "som levererar 2,05 megajoule (MJ) energi till målet, vilket resulterar i 3,15 MJ fusionsenergi.
Före detta genombrott hade kontrollerade fusionsreaktioner inte kunnat producera break-even (självuppehållande) kontrollerad fusion. De två mest avancerade metoderna för det är magnetisk inneslutning (toroiddesign) och tröghetsinneslutning (laserdesign). Fungerbara konstruktioner för en toroidformad reaktor som teoretiskt kommer att leverera tio gånger mer fusionsenergi än den mängd som behövs för att värma plasma till de erforderliga temperaturerna är under utveckling (se ITER ). ITER-anläggningen förväntas avsluta sin byggfas 2025. Den kommer att börja driftsätta reaktorn samma år och initiera plasmaexperiment 2025, men förväntas inte påbörja fullständig deuterium-tritiumfusion förrän 2035.
privat finansiering bara under 2021, och gick till många anmärkningsvärda startups inklusive men inte begränsat till Commonwealth Fusion Systems , Helion Energy Inc. , TAE Technologies Inc. och Zap Energy Inc.
På liknande sätt siktar kanadensisk-baserade General Fusion , som utvecklar ett magnetiserat kärnenergisystem för målfusion, att bygga sin demonstrationsanläggning till 2025.
Bearbeta
Frigörandet av energi med sammansmältningen av lätta element beror på samspelet mellan två motsatta krafter: kärnkraften, en manifestation av den starka interaktionen , som håller protoner och neutroner tätt samman i atomkärnan ; och Coulomb-kraften , som gör att positivt laddade protoner i kärnan stöter bort varandra. Lättare kärnor (kärnor mindre än järn och nickel) är tillräckligt små och protonfattiga för att tillåta kärnkraften att övervinna Coulombkraften. Detta beror på att kärnan är tillräckligt liten för att alla nukleoner ska känna den korta räckvidds attraktionskraften minst lika starkt som de känner avstötningen av Coulomb med oändligt räckvidd. Att bygga upp kärnor från lättare kärnor genom fusion frigör extra energi från nettoattraktionen av partiklar. För större kärnor frigörs dock ingen energi, eftersom kärnkraften är kortdistanserad och inte kan verka över större kärnor.
Fusion driver stjärnor och producerar praktiskt taget alla element i en process som kallas nukleosyntes . Solen är en huvudsekvensstjärna och genererar som sådan sin energi genom kärnfusion av vätekärnor till helium. I sin kärna smälter solen samman 620 miljoner ton väte och gör 616 miljoner ton helium varje sekund. Fusionen av lättare grundämnen i stjärnor frigör energi och den massa som alltid följer med den. Till exempel, vid sammansmältning av två vätekärnor för att bilda helium, förs 0,645% av massan bort i form av kinetisk energi av en alfapartikel eller andra former av energi, såsom elektromagnetisk strålning.
Det krävs avsevärd energi för att tvinga kärnorna att smälta samman, även de av det lättaste grundämnet, väte . När de accelereras till tillräckligt höga hastigheter kan kärnor övervinna denna elektrostatiska repulsion och föras tillräckligt nära så att den attraktiva kärnkraften är större än den repulsiva Coulomb-kraften. Den starka kraften växer snabbt när kärnorna är tillräckligt nära, och de sammansmältande nukleonerna kan i huvudsak "falla" in i varandra och resultatet är fusion och producerad nettoenergi. Fusionen av lättare kärnor, som skapar en tyngre kärna och ofta en fri neutron eller proton, frigör i allmänhet mer energi än vad som krävs för att tvinga samman kärnorna; detta är en exoterm process som kan producera självuppehållande reaktioner. [ citat behövs ]
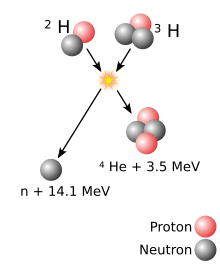
Energi som frigörs i de flesta kärnreaktioner är mycket större än i kemiska reaktioner , eftersom bindningsenergin som håller ihop en kärna är större än energin som håller elektroner till en kärna. Till exempel joniseringsenergin som erhålls genom att lägga till en elektron till en vätekärna 13,6 eV - mindre än en miljondel av de 17,6 MeV som frigörs i deuterium - tritium (D-T)-reaktionen som visas i det intilliggande diagrammet. Fusionsreaktioner har en energitäthet som är många gånger större än kärnklyvning ; reaktionerna producerar mycket större energi per massenhet även om individuella fissionsreaktioner i allmänhet är mycket mer energiska än individuella fusionsreaktioner, som i sig är miljontals gånger mer energiska än kemiska reaktioner. Endast direkt omvandling av massa till energi , som den som orsakas av den förintande kollisionen mellan materia och antimateria , är mer energisk per massaenhet än kärnfusion. (En fullständig omvandling av ett gram materia skulle frigöra 9 × 10 13 joule energi.)
Kärnfusion i stjärnor
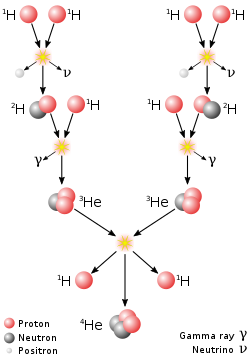
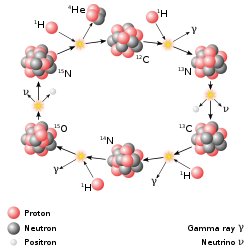
En viktig fusionsprocess är stjärnnukleosyntesen som driver stjärnor , inklusive solen. På 1900-talet insåg man att energin som frigörs från kärnfusionsreaktioner står för livslängden hos stjärnvärme och ljus. Fusionen av kärnor i en stjärna, med utgångspunkt från dess ursprungliga väte- och heliummängd, ger den energin och syntetiserar nya kärnor. Olika reaktionskedjor är inblandade, beroende på stjärnans massa (och därmed trycket och temperaturen i dess kärna).
Runt 1920 förutsåg Arthur Eddington upptäckten och mekanismen för kärnfusionsprocesser i stjärnor, i sin tidning The Internal Constitution of the Stars . Vid den tiden var källan till stjärnenergi okänd; Eddington spekulerade korrekt att källan var fusion av väte till helium, vilket frigjorde enorm energi enligt Einsteins ekvation E = mc 2 . Detta var en särskilt anmärkningsvärd utveckling eftersom fusion och termonukleär energi vid den tiden ännu inte hade upptäckts, och inte ens att stjärnor till stor del består av väte (se metallicitet ). Eddingtons tidning resonerade att:
- Den ledande teorin om stjärnenergi, kontraktionshypotesen, borde få en stjärnas rotation att synbart snabba upp på grund av bevarandet av rörelsemängd . Men observationer av Cepheid variabla stjärnor visade att detta inte hände.
- Den enda andra kända rimliga energikällan var omvandling av materia till energi; Einstein hade några år tidigare visat att en liten mängd materia motsvarade en stor mängd energi.
- Francis Aston hade också nyligen visat att massan av en heliumatom var cirka 0,8 % mindre än massan av de fyra väteatomerna som tillsammans skulle bilda en heliumatom (enligt den då rådande teorin om atomstruktur som höll atomvikten att vara den särskiljande egenskapen mellan grundämnen; arbete av Henry Moseley och Antonius van den Broek skulle senare visa att nukleinladdning var den särskiljande egenskapen och att en heliumkärna därför bestod av två vätekärnor plus ytterligare massa). Detta antydde att om en sådan kombination kunde hända, skulle den frigöra avsevärd energi som en biprodukt.
- Om en stjärna bara innehöll 5 % smältbart väte skulle det räcka för att förklara hur stjärnor fick sin energi. (det är nu känt att de flesta "vanliga" stjärnor innehåller mycket mer än 5 % väte.)
- Ytterligare grundämnen kan också smälta samman, och andra forskare hade spekulerat i att stjärnor var "degeln" där lätta grundämnen kombinerades för att skapa tunga grundämnen, men utan mer exakta mätningar av deras atommassa kunde inget mer sägas vid den tiden .
Alla dessa spekulationer visade sig vara korrekta under de följande decennierna.
Den primära källan till solenergi, och den för stjärnor av liknande storlek, är sammansmältningen av väte för att bilda helium (proton -proton-kedjereaktionen), som sker vid en sol-kärntemperatur på 14 miljoner kelvin. Nettoresultatet är sammansmältningen av fyra protoner till en alfapartikel , med frigörandet av två positroner och två neutriner (som förändrar två av protonerna till neutroner) och energi. I tyngre stjärnor CNO-cykeln och andra processer viktigare. När en stjärna förbrukar en betydande del av sitt väte, börjar den syntetisera tyngre grundämnen. De tyngsta grundämnena syntetiseras genom fusion som uppstår när en mer massiv stjärna genomgår en våldsam supernova i slutet av sin livstid, en process som kallas supernovanukleosyntes .
Krav
En betydande energibarriär av elektrostatiska krafter måste övervinnas innan fusion kan ske. På stora avstånd stöter två nakna kärnor bort varandra på grund av den frånstötande elektrostatiska kraften mellan deras positivt laddade protoner. Om två kärnor kan föras tillräckligt nära varandra, kan emellertid den elektrostatiska repulsionen övervinnas av kvanteffekten där kärnor kan tunnla genom coulombkrafter.
När en nukleon som en proton eller neutron läggs till en kärna, attraherar kärnkraften den till alla andra nukleoner i kärnan (om atomen är tillräckligt liten), men i första hand till sina närmaste grannar på grund av den korta räckvidden av kärnan. tvinga. Nukleonerna i det inre av en kärna har fler angränsande nukleoner än de på ytan. Eftersom mindre kärnor har ett större förhållande mellan yta och volym, ökar bindningsenergin per nukleon på grund av kärnkraften i allmänhet med storleken på kärnan men närmar sig ett gränsvärde som motsvarar det för en kärna med en diameter på cirka fyra nukleoner. Det är viktigt att komma ihåg att nukleoner är kvantobjekt . Så, till exempel, eftersom två neutroner i en kärna är identiska med varandra, är målet att skilja den ena från den andra, som vilken som finns i det inre och vilken som finns på ytan, faktiskt meningslöst, och inkluderingen av kvantmekanik är därför nödvändig för korrekta beräkningar.
Den elektrostatiska kraften, å andra sidan, är en omvänd kvadratisk kraft , så en proton som läggs till en kärna kommer att känna en elektrostatisk repulsion från alla andra protoner i kärnan. Den elektrostatiska energin per nukleon på grund av den elektrostatiska kraften ökar alltså obegränsat när kärnans atomnummer växer.
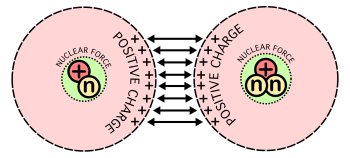
Nettoresultatet av de motstående elektrostatiska och starka kärnkrafterna är att bindningsenergin per nukleon i allmänhet ökar med ökande storlek, upp till grundämnena järn och nickel , och sedan minskar för tyngre kärnor. Så småningom bindningsenergin negativ och mycket tunga kärnor (alla med mer än 208 nukleoner, motsvarande en diameter på ca 6 nukleoner) är inte stabila. De fyra mest tätt bundna kärnorna, i fallande ordning av bindningsenergi per nukleon, är 62
Ni
, 58
Fe
, 56
Fe
och 60
Ni
. Även om nickelisotopen 62
Ni
är mer stabil är järnisotopen 56
Fe
en storleksordning vanligare . Detta beror på det faktum att det inte finns något enkelt sätt för stjärnor att skapa 62
Ni
genom alfaprocessen .
Ett undantag från denna allmänna trend är helium-4 -kärnan, vars bindningsenergi är högre än för litium , nästa tyngre grundämne. Detta beror på att protoner och neutroner är fermioner , som enligt Paulis uteslutningsprincip inte kan existera i samma kärna i exakt samma tillstånd. Varje proton eller neutrons energitillstånd i en kärna kan rymma både en spin up partikel och en spin down partikel. Helium-4 har en onormalt stor bindningsenergi eftersom dess kärna består av två protoner och två neutroner (det är en dubbelt magisk kärna), så alla dess fyra nukleoner kan vara i grundtillståndet. Eventuella ytterligare nukleoner skulle behöva gå in i högre energitillstånd. Helium-4-kärnan är faktiskt så hårt bunden att den vanligtvis behandlas som en enda kvantmekanisk partikel i kärnfysik, nämligen alfapartikeln .
Situationen är liknande om två kärnor sammanförs. När de närmar sig varandra stöter alla protoner i en kärna bort alla protoner i den andra. Inte förrän de två kärnorna faktiskt kommer tillräckligt nära under tillräckligt lång tid så att den starka kärnkraften kan ta över (genom tunnling) övervinns den frånstötande elektrostatiska kraften. Följaktligen, även när det slutliga energitillståndet är lägre, finns det en stor energibarriär som först måste övervinnas. Det kallas för Coulomb-barriären .
Coulomb -barriären är minst för isotoper av väte, eftersom deras kärnor bara innehåller en enda positiv laddning. En diproton är inte stabil, så neutroner måste också vara inblandade, helst på ett sådant sätt att en heliumkärna med sin extremt täta bindning är en av produkterna.
Med deuterium-tritiumbränsle är den resulterande energibarriären cirka 0,1 MeV. Som jämförelse är energin som behövs för att avlägsna en elektron från väte 13,6 eV. Det (mellanliggande) resultatet av fusionen är en instabil 5 He-kärna, som omedelbart skjuter ut en neutron med 14,1 MeV. Rekylenergin för den återstående 4 He-kärnan är 3,5 MeV, så den totala frigjorda energin är 17,6 MeV. Detta är många gånger mer än vad som behövdes för att övervinna energibarriären.
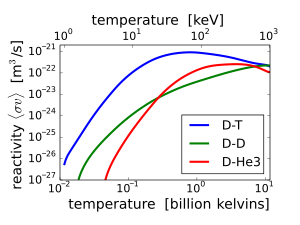
Reaktionstvärsnittet (σ) är ett mått på sannolikheten för en fusionsreaktion som en funktion av den relativa hastigheten för de två reaktantkärnorna . Om reaktanterna har en fördelning av hastigheter, t.ex. en termisk fördelning, är det användbart att utföra ett medelvärde över fördelningarna av produkten av tvärsnitt och hastighet. Detta medelvärde kallas 'reaktivitet', betecknat ⟨ σv ⟩ . Reaktionshastigheten (fusioner per volym per gång) är ⟨ σv ⟩ gånger produkten av reaktanternas taldensiteter:
Om en art av kärnor reagerar med en kärna som den själv, såsom DD-reaktionen, måste produkten ersättas med .
ökar från praktiskt taget noll vid rumstemperatur upp till meningsfulla magnituder vid temperaturer på 10 – 100 keV. Vid dessa temperaturer, långt över typiska joniseringsenergier (13,6 eV i vätefallet), existerar fusionsreaktanterna i ett plasmatillstånd .
Betydelsen av som en funktion av temperaturen i en enhet med en viss energiinneslutningstid hittas genom att betrakta Lawson-kriteriet . Detta är en extremt utmanande barriär att övervinna på jorden, vilket förklarar varför fusionsforskning har tagit många år att nå det nuvarande avancerade tekniska tillståndet.
Konstgjord fusion
Termonukleär fusion
Om materia är tillräckligt uppvärmd (därav plasma ) och instängd, kan fusionsreaktioner inträffa på grund av kollisioner med extrema termiska kinetiska energier hos partiklarna. Termonukleära vapen producerar vad som motsvarar en okontrollerad frisättning av fusionsenergi . Koncept för kontrollerad termonukleär fusion använder magnetiska fält för att begränsa plasman.
Tröghetsinneslutningsfusion
Inertial confinement fusion (ICF) är en metod som syftar till att frigöra fusionsenergi genom att värma och komprimera ett bränslemål, vanligtvis en pellet som innehåller deuterium och tritium .
Tröghetselektrostatisk inneslutning
Tröghetselektrostatisk inneslutning är en uppsättning enheter som använder ett elektriskt fält för att värma joner till fusionsförhållanden. Den mest kända är fusorn . Från och med 1999 har ett antal amatörer kunnat göra amatörfusion med dessa hemmagjorda enheter. Andra IEC-enheter inkluderar: Polywell , MIX POPS och Marble-koncepten.
Beam–beam eller beam–target fusion
Acceleratorbaserad ljus-jonfusion är en teknik som använder partikelacceleratorer för att uppnå partikelkinetiska energier som är tillräckliga för att inducera ljus-jonfusionsreaktioner. Acceleration av ljusjoner är relativt lätt och kan göras på ett effektivt sätt - kräver endast ett vakuumrör, ett par elektroder och en högspänningstransformator; fusion kan observeras med så lite som 10 kV mellan elektroderna. Systemet kan arrangeras för att accelerera joner till ett statiskt bränsleinfunderat mål, känt som beam-target fusion, eller genom att accelerera två strömmar av joner mot varandra, beam-beam fusion.
Huvudproblemet med acceleratorbaserad fusion (och med kalla mål i allmänhet) är att fusionstvärsnitt är många storleksordningar lägre än Coulomb-interaktionstvärsnitt. Därför förbrukar den stora majoriteten av joner sin energi genom att avge bremsstrahlung strålning och jonisering av atomer i målet. Enheter som kallas neutrongeneratorer med förseglade rör är särskilt relevanta för denna diskussion. Dessa små enheter är miniatyrpartikelacceleratorer fyllda med deuterium och tritiumgas i ett arrangemang som gör att joner av dessa kärnor kan accelereras mot hydridmål, även innehållande deuterium och tritium, där fusion äger rum, vilket frigör ett flöde av neutroner. Hundratals neutrongeneratorer produceras årligen för användning inom petroleumindustrin där de används i mätutrustning för att lokalisera och kartlägga oljereserver.
Ett antal försök att återcirkulera de joner som "missar" kollisioner har gjorts genom åren. Ett av de mer kända försöken på 1970-talet var Migma , som använde en unik partikellagringsring för att fånga joner i cirkulära banor och återföra dem till reaktionsområdet. Teoretiska beräkningar som gjorts vid finansieringsöversynen pekade på att systemet skulle ha betydande svårigheter att skala upp för att innehålla tillräckligt med fusionsbränsle för att vara relevant som kraftkälla. Norman Rostoker ett nytt arrangemang som använder en fältomvänd konfiguration (FRC) som lagringssystem och fortsätter att studeras av TAE Technologies från och med 2021. Ett närbesläktat tillvägagångssätt är att slå samman två FRC:er som roterar i motsatta riktningar , som aktivt studeras av Helion Energy . Eftersom dessa tillvägagångssätt alla har jonenergier långt bortom Coulomb-barriären , föreslår de ofta användningen av alternativa bränslecykler som p- 11 B som är för svåra att försöka med konventionella tillvägagångssätt.
Muon-katalyserad fusion
Muonkatalyserad fusion är en fusionsprocess som sker vid vanliga temperaturer. Den studerades i detalj av Steven Jones i början av 1980-talet. Nettoenergiproduktion från denna reaktion har misslyckats på grund av den höga energi som krävs för att skapa myoner , deras korta halveringstid på 2,2 µs och den höga chansen att en myon kommer att binda till den nya alfapartikeln och därmed sluta katalysera fusion.
Andra principer

Vissa andra instängningsprinciper har undersökts.
- Antimateriainitierad fusion använder små mängder antimateria för att utlösa en liten fusionsexplosion. Detta har studerats främst i samband med att göra kärnkraftspulsframdrivning och rena fusionsbomber möjliga. Detta är inte i närheten av att bli en praktisk kraftkälla, på grund av kostnaden för att tillverka enbart antimateria.
- Pyroelektrisk fusion rapporterades i april 2005 av ett team vid UCLA . Forskarna använde en pyroelektrisk kristall uppvärmd från -34 till 7 °C (−29 till 45 °F) , kombinerad med en volframnål för att producera ett elektriskt fält på cirka 25 gigavolt per meter för att jonisera och accelerera deuteriumkärnor till ett erbiumdeuteridmål . Vid de uppskattade energinivåerna kan D–D-fusionsreaktionen inträffa, som producerar helium-3 och en 2,45 MeV neutron . Även om den är en användbar neutrongenerator, är apparaten inte avsedd för kraftgenerering eftersom den kräver mycket mer energi än den producerar. D–T-fusionsreaktioner har observerats med ett tritierat erbiummål.
- Kärnfusion-klyvningshybrid (hybrid kärnkraft) är ett föreslaget sätt att generera kraft genom att använda en kombination av kärnfusions- och klyvningsprocesser . Konceptet dateras till 1950-talet och förespråkades kort av Hans Bethe under 1970-talet, men förblev i stort sett outforskat tills intresset återupptogs 2009, på grund av förseningarna i förverkligandet av ren fusion.
- Projekt PACER , som genomfördes vid Los Alamos National Laboratory (LANL) i mitten av 1970-talet, undersökte möjligheten till ett fusionskraftsystem som skulle innebära att små vätebomber (fusionsbomber) exploderade i en underjordisk hålighet. Som energikälla är systemet det enda fusionskraftsystemet som kunde demonstreras fungera med hjälp av befintlig teknik. Men det skulle också kräva ett stort, kontinuerligt utbud av kärnvapenbomber, vilket gör ekonomin i ett sådant system ganska tveksam.
- Bubble fusion, även kallad sonofusion , var en föreslagen mekanism för att uppnå fusion via sonisk kavitation som blev framträdande i början av 2000-talet. Efterföljande försök till replikering misslyckades och huvudutredaren, Rusi Taleyarkhan , bedömdes skyldig till forskningsfel 2008.
Viktiga reaktioner
Stjärnreaktionskedjor
Vid temperaturer och tätheter i stjärnkärnor är hastigheten för fusionsreaktioner notoriskt långsamma. Till exempel, vid solkämens temperatur ( T ≈ 15 MK) och densitet (160 g/cm 3 ), är energifrisättningshastigheten endast 276 μW/cm 3 - ungefär en fjärdedel av den volymetriska hastigheten med vilken en vilande människokropp genererar värme . Således är reproduktion av stjärnkärnförhållanden i ett labb för kärnfusionskraftproduktion helt opraktisk. Eftersom kärnreaktionshastigheter beror på såväl densitet som temperatur och de flesta fusionsscheman fungerar vid relativt låga densiteter, är dessa metoder starkt beroende av högre temperaturer. Fusionshastigheten som funktion av temperatur (exp(− E / kT )), leder till behovet av att uppnå temperaturer i terrestra reaktorer 10–100 gånger högre än i stjärninteriörer: T ≈ (0,1–1,0) × 10 9 K .
Kriterier och kandidater för terrestra reaktioner
Vid artificiell fusion är det primära bränslet inte begränsat till att vara protoner och högre temperaturer kan användas, så reaktioner med större tvärsnitt väljs. Ett annat bekymmer är produktionen av neutroner, som aktiverar reaktorstrukturen radiologiskt, men som också har fördelarna att tillåta volymetrisk extraktion av fusionsenergin och tritiumförädling . Reaktioner som inte frigör några neutroner kallas aneutroniska .
För att vara en användbar energikälla måste en fusionsreaktion uppfylla flera kriterier. Det måste:
- Var exoterm
- Detta begränsar reaktanterna till den låga Z- sidan (antal protoner) av kurvan för bindningsenergi . Det gör också helium 4
He
till den vanligaste produkten på grund av dess utomordentligt täta bindning, även om 3
He
och 3
H
också dyker upp. Involvera - kärnor med lågt atomnummer ( Z
- ) Detta beror på att den elektrostatiska repulsionen som måste övervinnas innan kärnorna är tillräckligt nära för att smälta är direkt relaterad till antalet protoner den innehåller – dess atomnummer. [ citat behövs ]
- Har två reaktanter
- Vid något mindre än stjärndensiteter är trekroppskollisioner för osannolika. Vid tröghetsinneslutning överskrids både stjärndensiteter och temperaturer för att kompensera för bristerna i den tredje parametern i Lawson-kriteriet, ICF:s mycket korta inneslutningstid.
- Har två eller flera produkter
- Detta möjliggör samtidig bevarande av energi och momentum utan att förlita sig på den elektromagnetiska kraften.
- Bevara både protoner och neutroner
- Tvärsnitten för den svaga interaktionen är för små.
Få reaktioner uppfyller dessa kriterier. Följande är de med störst tvärsnitt:
(1)
2 1 D
+
3 1 T
→
4 2 Han
( 3,52 MeV ) + n0 ( 14,06 MeV ) (2i)
2 1 D
+
2 1 D
→
3 1 T
( 1,01 MeV ) + p + ( 3,02 MeV ) 50 % (2ii) →
3 2 Han
( 0,82 MeV ) + n0 ( 2,45 MeV ) 50 % (3)
2 1 D
+
3 2 Han
→
4 2 Han
( 3,6 MeV ) + p + ( 14,7 MeV ) (4)
3 1 T
+
3 1 T
→
4 2 Han
+ 2 n 0 + 11,3 MeV (5)
3 2 Han
+
3 2 Han
→
4 2 Han
+ 2 p + + 12,9 MeV (6i)
3 2 Han
+
3 1 T
→
4 2 Han
+ p + + n0 + 12,1 MeV 57 % (6ii) →
4 2 Han
( 4,8 MeV ) +
2 1 D
( 9,5 MeV ) 43 % (7i)
2 1 D
+
6 3 Li
→ 2
4 2 Han
+ 22,4 MeV (7ii) →
3 2 Han
+
4 2 Han
+ n0 + 2,56 MeV (7iii) →
7 3 Li
+ p + + 5,0 MeV (7iv) →
7 4 Var
+ n0 + 3,4 MeV (8) p + +
6 3 Li
→
4 2 Han
( 1,7 MeV ) +
3 2 Han
( 2,3 MeV ) (9)
3 2 Han
+
6 3 Li
→ 2
4 2 Han
+ p + + 16,9 MeV (10) p + +
11 5 B
→ 3
4 2 Han
+ 8,7 MeV
| Nukleosyntes |
|---|
 |
| Relaterade ämnen |
För reaktioner med två produkter delas energin mellan dem i omvänd proportion till deras massor, som visas. I de flesta reaktioner med tre produkter varierar fördelningen av energi. För reaktioner som kan resultera i mer än en uppsättning produkter anges förgreningsförhållandena.
Vissa reaktionskandidater kan elimineras på en gång. D– 6 Li-reaktionen har ingen fördel jämfört med p + –
11 5 B
eftersom den är ungefär lika svår att bränna men producerar betydligt fler neutroner genom
2 1 D
–
2 1 D
sidreaktioner. Det finns också en p + –
7 3 Li
-reaktion, men tvärsnittet är alldeles för lågt, förutom möjligen när Ti > 1 MeV, men vid så höga temperaturer blir också en endoterm, direkt neutronproducerande reaktion mycket signifikant. Slutligen finns det också en p + –
9 4 Be
-reaktion, som inte bara är svår att bränna, utan
9 4 Be
lätt kan induceras att delas i två alfapartiklar och en neutron.
Förutom fusionsreaktionerna är följande reaktioner med neutroner viktiga för att "föda upp" tritium i "torra" fusionsbomber och några föreslagna fusionsreaktorer:
Den senare av de två ekvationerna var okänd när USA genomförde Castle Bravo fusionsbombtestet 1954. Eftersom det bara var den andra fusionsbomben som någonsin testats (och den första som använde litium), hade designarna av Castle Bravo "Shrimp" förstått att användbarheten av 6 Li i tritiumproduktion, men hade misslyckats med att inse att 7 Li fission avsevärt skulle öka bombens utbyte. Medan 7 Li har ett litet neutrontvärsnitt för låg neutronenergi, har det ett högre tvärsnitt över 5 MeV. Skörden på 15 Mt var 150 % högre än de förutspådda 6 Mt och orsakade oväntad exponering för nedfall.
För att utvärdera användbarheten av dessa reaktioner behöver man, förutom reaktanterna, produkterna och den frigjorda energin, veta något om kärntvärsnittet . Varje given fusionsenhet har ett maximalt plasmatryck den kan upprätthålla, och en ekonomisk enhet skulle alltid fungera nära detta maximum. Givet detta tryck erhålls den största smälteffekten när temperaturen väljs så att ⟨ σv ⟩/ T 2 är ett maximum. Detta är också den temperatur vid vilken värdet på den trippelprodukt nTτ som krävs för antändning är ett minimum, eftersom det erforderliga värdet är omvänt proportionellt mot ⟨ σv ⟩/ T 2 (se Lawson-kriteriet ). (Ett plasma "antänds" om fusionsreaktionerna producerar tillräckligt med kraft för att upprätthålla temperaturen utan extern uppvärmning.) Denna optimala temperatur och värdet på ⟨ σv ⟩/ T 2 vid den temperaturen ges för några av dessa reaktioner i följande tabell.
| bränsle | T [keV] | ⟨ σv ⟩/ T 2 [m 3 /s/keV 2 ] |
|---|---|---|
|
2 1 D – 3 1 T |
13.6 | 1,24 × 10 −24 |
|
2 1 D – 2 1 D |
15 | 1,28 × 10 −26 |
|
2 1 D – 3 2 He |
58 | 2,24 × 10 −26 |
| p + – 6 3 Li |
66 | 1,46 × 10 −27 |
| p + – 11 5 B |
123 | 3,01 × 10 -27 |
Observera att många av reaktionerna bildar kedjor. Till exempel skapar en reaktor som drivs med
3 1 T
och
3 2 He
några
2 1 D
, som sedan är möjliga att använda i
2 1 D
–
3 2 He
-reaktionen om energierna är "rätt". En elegant idé är att kombinera reaktionerna (8) och (9). 3 (
2 He
från reaktion (8) kan reagera med
6 3 Li i reaktion
9) innan den termaliseras fullständigt. Detta producerar en energisk proton, som i sin tur genomgår reaktion (8) innan den termaliseras. Detaljerad analys visar att denna idé inte skulle fungera bra, [ citat behövs ] men det är ett bra exempel på ett fall där det vanliga antagandet om en Maxwellsk plasma inte är lämplig.
Överflöd av kärnfusionsbränslen
| Kärnfusionsbränsleisotop | Halveringstid | Överflöd |
|---|---|---|
|
1 1 H |
Stabil | 99,98 % |
|
2 1 D |
Stabil | 0,02 % |
|
3 1 T |
12.32(2) y | spår |
|
3 2 Han |
stabil | 0,0002 % |
|
6 3 Li |
stabil | 7,59 % |
|
7 3 Li |
stabil | 92,41 % |
|
11 5 B |
stabil | 80 % |
|
12 6 C |
stabil | 98,9 % |
|
13 6 C |
stabil | 1,1 % |
|
13 7 N |
9,965(4) min | syn |
|
14 7 N |
stabil | 99,6 % |
|
15 7 N |
stabil | 0,4 % |
|
14 8 O |
70.621(11) s | syn |
|
15 8 O |
122.266(43) s | syn |
|
16 8 O |
stabil | 99,76 % |
|
17 8 O |
stabil | 0,04 % |
|
18 8 O |
stabil | 0,20 % |
|
17 9 F |
64.370(27) s | syn |
|
18 9 F |
109,734(8) min | spår |
|
19 9 F |
stabil | 100 % |
Neutronicitet, inneslutningskrav och effekttäthet
Vilken som helst av reaktionerna ovan kan i princip ligga till grund för fusionskraftproduktion . Utöver temperaturen och tvärsnittet som diskuterats ovan måste vi beakta den totala energin hos fusionsprodukterna E fus , energin hos de laddade fusionsprodukterna Ech och atomnumret Z för den icke-vätehaltiga reaktanten.
Specifikation av
2 1 D
–
2 1 D
reaktionen medför dock vissa svårigheter. Till att börja med måste man snitta över de två grenarna (2i) och (2ii). Svårare är att bestämma hur man ska behandla
3 1 T
och
3 2 He
produkterna.
3 1 T
brinner så bra i en deuteriumplasma att det är nästan omöjligt att extrahera från plasman. 2 -
1 D
–
3 2 He
-reaktionen är optimerad vid en mycket högre temperatur, så utbränningen vid den optimala
2 1 D
–
2 1 D
temperaturen kan vara låg. Därför verkar det rimligt att anta att
3 1 T
men inte
3 2 He
bränns upp och adderar sin energi till nettoreaktionen, vilket innebär att den totala reaktionen skulle vara summan av (2i), (2ii) och (1) ):
- 5
2 1 D
→
4 2 He
+ 2 n 0 +
3 2 He
+ p + , E fus = 4,03 + 17,6 + 3,27 = 24,9 MeV, E ch = 4,03 + 3,5 + 0,82 = 8,35 MeV.
För att beräkna effekten av en reaktor (där reaktionshastigheten bestäms av D–D-steget), räknar vi
2 1 D
–
2 1 D
fusionsenergin per D–D-reaktion som E fus = (4,03 MeV + 17,6 MeV ) × 50% + (3,27 MeV) × 50% = 12,5 MeV och energin i laddade partiklar som E ch = (4,03 MeV + 3,5 MeV) × 50% + (0,82 MeV) × 50% = 4,2 MeV. (Notera: om tritiumjonen reagerar med en deuteron medan den fortfarande har en stor kinetisk energi, så kan den kinetiska energin för helium-4 som produceras vara helt annorlunda än 3,5 MeV, så denna beräkning av energi i laddade partiklar är bara en approximation av genomsnittet.) Mängden energi per förbrukad deuteron är 2/5 av detta, eller 5,0 MeV (en specifik energi på cirka 225 miljoner MJ per kilogram deuterium).
En annan unik aspekt av
2 1 D
–
2 1 D
-reaktionen är att det bara finns en reaktant, som måste beaktas vid beräkning av reaktionshastigheten.
Med detta val tar vi upp parametrar för fyra av de viktigaste reaktionerna
| bränsle | Z | E fus [MeV] | E ch [MeV] | neutronicitet |
|---|---|---|---|---|
|
2 1 D – 3 1 T |
1 | 17.6 | 3.5 | 0,80 |
|
2 1 D – 2 1 D |
1 | 12.5 | 4.2 | 0,66 |
|
2 1 D – 3 2 He |
2 | 18.3 | 18.3 | ≈0,05 |
| p + – 11 5 B |
5 | 8.7 | 8.7 | ≈0,001 |
Den sista kolumnen är reaktionens neutronicitet , den del av fusionsenergin som frigörs som neutroner. Detta är en viktig indikator på omfattningen av problemen i samband med neutroner som strålningsskador, biologisk avskärmning, fjärrhantering och säkerhet. För de två första reaktionerna beräknas det som ( E fus − E ch )/ E fus . För de två sista reaktionerna, där denna beräkning skulle ge noll, är de angivna värdena grova uppskattningar baserade på sidoreaktioner som producerar neutroner i ett plasma i termisk jämvikt.
Naturligtvis bör reaktanterna också blandas i optimala proportioner. Detta är fallet när varje reaktantjon plus dess tillhörande elektroner står för halva trycket. Om man antar att det totala trycket är fixerat betyder detta att partikeldensiteten för den icke-vätejonen är mindre än den för vätejonen med en faktor 2/( Z + 1) . Därför reduceras hastigheten för dessa reaktioner med samma faktor, utöver eventuella skillnader i värdena på ⟨ σv ⟩/ T 2 . Å andra sidan, eftersom
2 1 D
–
2 1 D
-reaktionen bara har en reaktant, är dess hastighet dubbelt så hög som när bränslet delas mellan två olika väteämnen, vilket skapar en mer effektiv reaktion.
Det finns alltså en "straffstraff" på 2/( Z + 1) för icke-vätebränslen som härrör från det faktum att de kräver fler elektroner, som tar upp tryck utan att delta i fusionsreaktionen. (Det är vanligtvis ett bra antagande att elektrontemperaturen kommer att vara nästan lika med jontemperaturen. Vissa författare diskuterar dock möjligheten att elektronerna skulle kunna hållas betydligt kallare än jonerna. I ett sådant fall, känt som en "het" jonläge", skulle "straffet" inte gälla.) Det finns samtidigt en "bonus" på en faktor 2 för
2 1 D
–
2 1 D
eftersom varje jon kan reagera med vilken som helst av de andra jonerna, inte bara en bråkdel av dem.
Vi kan nu jämföra dessa reaktioner i följande tabell.
| bränsle | ⟨ σv ⟩/ T 2 | straff/bonus | omvänd reaktivitet | Lawson kriterium | effekttäthet [W/m 3 /kPa 2 ] | omvänt förhållande mellan effekttäthet |
|---|---|---|---|---|---|---|
|
2 1 D – 3 1 T |
1,24 × 10 −24 | 1 | 1 | 1 | 34 | 1 |
|
2 1 D – 2 1 D |
1,28 × 10 −26 | 2 | 48 | 30 | 0,5 | 68 |
|
2 1 D – 3 2 He |
2,24 × 10 −26 | 2/3 | 83 | 16 | 0,43 | 80 |
| p + – 6 3 Li |
1,46 × 10 −27 | 1/2 | 1700 | 0,005 | 6800 | |
| p + – 11 5 B |
3,01 × 10 −27 | 1/3 | 1240 | 500 | 0,014 | 2500 |
Det maximala värdet på ⟨ σv ⟩/ T 2 är hämtat från en tidigare tabell. "Straff/bonus"-faktorn är den som är relaterad till en icke-vätereaktant eller en reaktion av en art. Värdena i kolumnen "invers reaktivitet" hittas genom att dividera 1,24 × 10 −24 med produkten av den andra och tredje kolumnen. Det indikerar den faktor med vilken de andra reaktionerna sker långsammare än
2 1 D
–
3 1 T
-reaktionen under jämförbara förhållanden. Kolumnen " Lawson-kriterium " viktar dessa resultat med E ch och ger en indikation på hur mycket svårare det är att uppnå antändning med dessa reaktioner, i förhållande till svårigheten för
2 1 D
–
3 1 T
-reaktionen. Den näst sista kolumnen är märkt "effektdensitet" och väger den praktiska reaktiviteten med E fus . Den sista kolumnen anger hur mycket lägre fusionseffekttätheten för de andra reaktionerna är jämfört med
2 1 D
–
3 1 T
-reaktionen och kan betraktas som ett mått på den ekonomiska potentialen.
Bremsstrahlung förluster i kvasineutrala, isotropa plasma
Jonerna som genomgår fusion i många system kommer i princip aldrig att uppstå ensamma utan kommer att blandas med elektroner som sammantaget neutraliserar jonernas elektriska laddning och bildar ett plasma . Elektronerna kommer i allmänhet att ha en temperatur som är jämförbar med eller högre än jonernas, så de kommer att kollidera med jonerna och avge röntgenstrålning med 10–30 keV energi, en process som kallas Bremsstrahlung .
Den enorma storleken på solen och stjärnorna gör att röntgenstrålningen som produceras i denna process inte kommer att försvinna och kommer att deponera sin energi tillbaka i plasman. De sägs vara ogenomskinliga för röntgenstrålar. Men vilken jordbunden fusionsreaktor som helst kommer att vara optiskt tunn för röntgenstrålar av detta energiområde. Röntgenstrålar är svåra att reflektera men de absorberas effektivt (och omvandlas till värme) i mindre än mm tjocklek av rostfritt stål (som är en del av en reaktorsköld). Detta innebär att bremsstrahlung-processen för energi ut ur plasman och kyler den.
Förhållandet mellan fusionskraft som produceras och röntgenstrålning som går förlorad till väggar är en viktig förtjänstsiffra. Detta förhållande är i allmänhet maximerat vid en mycket högre temperatur än den som maximerar effekttätheten (se föregående underavsnitt). Följande tabell visar uppskattningar av den optimala temperaturen och effektförhållandet vid den temperaturen för flera reaktioner:
| bränsle | T i [keV] | P fusion / P Bremsstrahlung |
|---|---|---|
|
2 1 D – 3 1 T |
50 | 140 |
|
2 1 D – 2 1 D |
500 | 2.9 |
|
2 1 D – 3 2 He |
100 | 5.3 |
|
3 2 He – 3 2 He |
1000 | 0,72 |
| p + – 6 3 Li |
800 | 0,21 |
| p + – 11 5 B |
300 | 0,57 |
De faktiska förhållandena mellan fusion och Bremsstrahlungs kraft kommer sannolikt att vara betydligt lägre av flera skäl. För det första antar beräkningen att fusionsprodukternas energi överförs helt till bränslejonerna, som sedan förlorar energi till elektronerna vid kollisioner, som i sin tur förlorar energi genom Bremsstrahlung. Men eftersom fusionsprodukterna rör sig mycket snabbare än bränslejonerna kommer de att ge upp en betydande del av sin energi direkt till elektronerna. För det andra antas jonerna i plasman vara rena bränslejoner. I praktiken kommer det att finnas en betydande andel föroreningsjoner, vilket då kommer att sänka förhållandet. måste själva fusionsprodukterna förbli i plasman tills de har gett upp sin energi, och kommer att finnas kvar en tid efter det i alla föreslagna inneslutningssystem. Slutligen har alla andra kanaler för energiförlust än Bremsstrahlung försummats. De två sista faktorerna är relaterade. På teoretiska och experimentella grunder verkar partikel- och energiinneslutning vara nära besläktad. I ett system för inneslutning som gör ett bra jobb med att behålla energi, kommer fusionsprodukter att byggas upp. Om fusionsprodukterna sprutas ut effektivt, blir energiinneslutningen också dålig.
Temperaturerna som maximerar fusionseffekten jämfört med Bremsstrahlung är i alla fall högre än den temperatur som maximerar effekttätheten och minimerar det erforderliga värdet för fusionstrippelprodukten . Detta kommer inte att förändra den optimala driftpunkten för
2 1 D
–
3 1 T
särskilt mycket eftersom Bremsstrahlung-fraktionen är låg, men det kommer att pressa de andra bränslena in i regimer där effekttätheten i förhållande till
2 1 D
–
3 1 T
är ännu lägre och den erforderliga inneslutningen ännu svårare att uppnå. För
2 1 D
–
2 1 D
och
2 1 D
–
3 2 He
, kommer Bremsstrahlung förluster att vara ett allvarligt, möjligen oöverkomligt problem. För
3 2 He
–
3 2 He
, p + –
6 3 Li
och p + –
11 5 B
verkar Bremsstrahlung-förlusterna göra en fusionsreaktor som använder dessa bränslen med en kvasineutral, isotrop plasma omöjlig. Vissa vägar ut ur detta dilemma har övervägts men avvisats. Denna begränsning gäller inte för icke-neutrala och anisotropa plasma ; dessa har dock sina egna utmaningar att brottas med.
Matematisk beskrivning av tvärsnitt
Fusion under klassisk fysik
I en klassisk bild kan kärnor förstås som hårda sfärer som stöter bort varandra genom Coulomb-kraften men smälter samman när de två sfärerna kommer tillräckligt nära för kontakt. Om man uppskattar radien för en atomkärna som ungefär en femtometer, är energin som behövs för fusion av två väte:
Detta skulle innebära att för solens kärna, som har en Boltzmann-fördelning med en temperatur på runt 1,4 keV, är sannolikheten för att väte skulle nå tröskeln det vill säga fusion skulle aldrig inträffa. Men fusion i solen sker på grund av kvantmekaniken.
Parametrering av tvärsnitt
Sannolikheten för att fusion sker är avsevärt ökad jämfört med den klassiska bilden, tack vare smetningen av den effektiva radien som de Broglie-våglängden samt kvanttunnlar genom potentialbarriären. För att bestämma hastigheten för fusionsreaktioner är det mest intressanta värdet tvärsnittet , som beskriver sannolikheten för att partiklar kommer att smälta genom att ge ett karakteristiskt område för interaktion. En uppskattning av fusionstvärsnittsarean är ofta uppdelad i tre delar:
där är det geometriska tvärsnittet, T är barriärtransparensen och R är reaktionens reaktionsegenskaper.
är av storleksordningen kvadraten på de Broglie-våglängden där är systemets reducerade massa och är systemets massenergicentrum.
T kan approximeras av Gamow-transparensen, som har formen: där är Gamow-faktorn och kommer från att uppskatta kvanttunnelsannolikheten genom den potentiella barriären.
R innehåller all kärnfysik för den specifika reaktionen och har mycket olika värden beroende på arten av interaktionen. Men för de flesta reaktioner är variationen av liten jämfört med variationen från Gamow-faktorn och approximeras därför av en funktion som kallas den astrofysiska S-faktorn , som är svagt varierande i energi. Om man sätter ihop dessa beroenden tar en approximation för fusionstvärsnittet som en funktion av energi formen:
Mer detaljerade former av tvärsnittet kan härledas genom kärnfysikbaserade modeller och R-matristeori .
Formler för fusionstvärsnitt
Naval Research Labs plasmafysikformel ger det totala tvärsnittet i ladugårdar som en funktion av energin (i keV) av den infallande partikeln mot en måljon i vila passform med formeln:
- med följande koefficientvärden:
| DT(1) | DD(2i) | DD(2ii) | DHe 3 (3) | TT(4) | DE 3 (6) | |
|---|---|---|---|---|---|---|
| A1 | 45,95 | 46,097 | 47,88 | 89,27 | 38,39 | 123,1 |
| A2 | 50200 | 372 | 482 | 25900 | 448 | 11250 |
| A3 | 1,368 × 10 −2 | 4,36 × 10 −4 | 3,08 × 10 −4 | 3,98 × 10 −3 | 1,02 × 10 −3 | 0 |
| A4 | 1,076 | 1.22 | 1,177 | 1,297 | 2.09 | 0 |
| A5 | 409 | 0 | 0 | 647 | 0 | 0 |
Bosch-Hale rapporterar också en R-matris beräknade tvärsnitt som passar observationsdata med Padé rationella approximeringskoefficienter . Med energi i enheter av keV och tvärsnitt i enheter av millibarn, har faktorn formen:
- med koefficientvärdena:
| DT(1) | DD(2ii) | DHe 3 (3) | DEN 4 | |
|---|---|---|---|---|
| 31,3970 | 68,7508 | 31,3970 | 34,3827 | |
| A1 | 5,5576 × 10 4 | 5,7501 × 10 6 | 5,3701 × 10 4 | 6,927 × 10 4 |
| A2 | 2,1054 × 10 2 | 2,5226 × 10 3 | 3,3027 × 10 2 | 7.454 × 10 8 |
| A3 | −3,2638 × 10 −2 | 4,5566 × 10 1 | −1,2706 × 10 −1 | 2 050 × 10 6 |
| A4 | 1,4987 × 10 −6 | 0 | 2,9327 × 10 −5 | 5,2002 × 10 4 |
| A5 | 1,8181 × 10 −10 | 0 | −2,5151 × 10 −9 | 0 |
| B1 | 0 | −3,1995 × 10 −3 | 0 | 6,38 × 10 1 |
| B2 | 0 | −8,5530 × 10 −6 | 0 | −9,95 × 10 −1 |
| B3 | 0 | 5,9014 × 10 −8 | 0 | 6,981 × 10 −5 |
| B4 | 0 | 0 | 0 | 1,728 × 10 −4 |
| Tillämpligt energiområde [keV] | 0,5–5000 | 0,3–900 | 0,5–4900 | 0,5–550 |
| 2.0 | 2.2 | 2.5 | 1.9 |
där
Maxwell-medelvärde för kärntvärsnitt
I fusionssystem som är i termisk jämvikt är partiklarna i en Maxwell-Boltzmann-fördelning , vilket betyder att partiklarna har en rad energier centrerade kring plasmatemperaturen. Solen, magnetiskt begränsade plasma och tröghetsinneslutningsfusionssystem är väl modellerade för att vara i termisk jämvikt. I dessa fall är värdet av intresse fusionstvärsnittet i genomsnitt över Maxwell-Boltzmann-fördelningen. Naval Research Labs plasmafysikformel tabellerar Maxwells genomsnittliga reaktivitet i fusionstvärsnitt i .
| Temperatur [keV] | DT(1) | DD(2ii) | DHe 3 (3) | TT(4) | De 3 (6) |
|---|---|---|---|---|---|
| 1 | 5,5 × 10 −21 | 1,5 × 10 −22 | 1,0 × 10 -26 | 3,3 × 10 −22 | 1,0 × 10 -28 |
| 2 | 2,6 × 10 −19 | 5,4 × 10 −21 | 1,4 × 10 −23 | 7,1 × 10 −21 | 1,0 × 10 -25 |
| 5 | 1,3 × 10 −17 | 1,8 × 10 −19 | 6,7 × 10 −21 | 1,4 × 10 −19 | 2,1 × 10 −22 |
| 10 | 1,1 × 10 −16 | 1,2 × 10 −18 | 2,3 × 10 −19 | 7,2 × 10 −19 | 1,2 × 10 −20 |
| 20 | 4,2 × 10 −16 | 5,2 × 10 −18 | 3,8 × 10 −18 | 2,5 × 10 −18 | 2,6 × 10 −19 |
| 50 | 8,7 × 10 −16 | 2,1 × 10 −17 | 5,4 × 10 −17 | 8,7 × 10 −18 | 5,3 × 10 −18 |
| 100 | 8,5 × 10 −16 | 4,5 × 10 −17 | 1,6 × 10 −16 | 1,9 × 10 −17 | 2,7 × 10 −17 |
| 200 | 6,3 × 10 −16 | 8,8 × 10 −17 | 2,4 × 10 −16 | 4,2 × 10 −17 | 9,2 × 10 −17 |
| 500 | 3,7 × 10 −16 | 1,8 × 10 −16 | 2,3 × 10 −16 | 8,4 × 10 −17 | 2,9 × 10 −16 |
| 1000 | 2,7 × 10 −16 | 2,2 × 10 −16 | 1,8 × 10 −16 | 8,0 × 10 −17 | 5,2 × 10 −16 |
För energier kan data representeras av:
med T i enheter av keV.
Se även
- China Fusion Engineering Test Reactor
- Kall fusion
- Fokusera fusion
- Fusenet
- Fusionsraket
- Impulsgenerator
- Joint European Torus
- Lista över fusionsexperiment
- Lista över Fusor-exempel
- Lista över plasma (fysik) artiklar
- Neutronkälla
- Kärnenergi
- Kärnfusion-fission hybrid
- Kärnfysik
- Kärnreaktor
- Nukleosyntes
- Periodiska systemet
- Pulserande kraft
- Rent fusionsvapen
- Teller–Ulam design
- Termonukleär fusion
- Tidslinje för kärnfusion
- Trippel-alfa-process
Vidare läsning
- "Vad är Nuclear Fusion?" . NuclearFiles.org. Arkiverad från originalet den 28 september 2006 . Hämtad 12 januari 2006 .
- S. Atzeni; J. Meyer-ter-Vehn (2004). "Kärnfusionsreaktioner" (PDF) . Tröghetsfusionens fysik . University of Oxford Press . ISBN 978-0-19-856264-1 . Arkiverad från originalet (PDF) den 24 januari 2005.
- G. Brumfiel (22 maj 2006). "Kaos kan hålla fusionen under kontroll". Naturen . doi : 10.1038/news060522-2 . S2CID 62598131 .
- RW Bussard (9 november 2006). "Ska Google gå till kärnkraft? Ren, billig, kärnkraft" . Google TechTalks . Arkiverad från originalet den 26 april 2007.
- A. Wenisch; R. Kromp; D. Reinberger (november 2007). "Science or Fiction: Finns det en framtid för kärnkraft?" (PDF) . Österrikiska institutet för ekologi.
- M. Kikuchi, K. Lackner & MQ Tran (2012). Fusionsfysik . Internationella atomenergiorganet . sid. 22. ISBN 9789201304100 .
- RK Janev, red. (1995). Atom- och molekylära processer i fusionskantplasma . Springer USA . ISBN 978-1-4757-9319-2 .
externa länkar
- NuclearFiles.org – Ett arkiv med dokument relaterade till kärnkraft.
- Kommenterad bibliografi för kärnfusion från Alsos Digital Library for Nuclear Issues
- NRL Fusion Formulary Arkiverad 26 oktober 2020 på Wayback Machine




![{\displaystyle E_{\ce {thresh}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {Z_{1}Z_{2}}{r}}{\ce {->[{\text{2 protons}}]}}{\frac {1}{4\pi \epsilon _{0}}}{\frac {e^{2}}{1\ {\ce {fm}}}}\approx 1.4\ {\ce {MeV}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca1291445cce7787dc6d8b4cdf069e51ab63d0dd)



















