Beta-förfall

β ⁻
sönderfall i en atomkärna (medföljande antineutrino utelämnas). Insättningen visar beta-sönderfall av en fri neutron. Ingen av dessa avbildningar visar den mellanliggande virtuella
W ⁻
bosonen.

Inom kärnfysik är beta-sönderfall (β-sönderfall) en typ av radioaktivt sönderfall där en beta-partikel (snabb energisk elektron eller positron ) sänds ut från en atomkärna och omvandlar den ursprungliga nukliden till en isobar av den nukliden . Till exempel, beta-sönderfall av en neutron omvandlar den till en proton genom emission av en elektron åtföljd av en antineutrino ; eller omvänt omvandlas en proton till en neutron genom emission av en positron med en neutrino i så kallad positronemission . Varken beta-partikeln eller dess associerade (anti-)neutrino existerar i kärnan före beta-sönderfallet, utan skapas i sönderfallsprocessen. Genom denna process får instabila atomer ett mer stabilt förhållande mellan protoner och neutroner . Sannolikheten för att en nuklid sönderfaller på grund av beta och andra former av sönderfall bestäms av dess nukleära bindningsenergi . Bindningsenergierna för alla befintliga nuklider bildar det som kallas stabilitetens kärnband eller dalgång . För att antingen elektron- eller positronemission ska vara energetiskt möjlig måste energifrisättningen ( se nedan ) eller Q -värdet vara positivt.

Beta-sönderfall är en följd av den svaga kraften , som kännetecknas av relativt långa sönderfallstider. Nukleoner är sammansatta av uppkvarkar och nedkvarkar , och den svaga kraften tillåter en kvark att ändra sin smak genom att utsända en W-boson som leder till skapandet av ett elektron/antineutrino- eller positron/neutrino-par. Till exempel, en neutron, som består av två nedkvarkar och en uppkvarkar, sönderfaller till en proton som består av en nedkvarkar och två uppkvarkar.

Elektronfångning ingår ibland som en typ av beta-sönderfall, eftersom den grundläggande kärnprocessen, förmedlad av den svaga kraften, är densamma. Vid elektronfångst fångas en inre atomelektron av en proton i kärnan, omvandlar den till en neutron, och en elektronneutrino frigörs.

Beskrivning

De två typerna av beta-förfall är kända som beta minus och beta plus . I beta minus (β ⁻ ) sönderfall omvandlas en neutron till en proton, och processen skapar en elektron och en elektron antineutrino ; medan i beta plus (β ⁺ ) sönderfall omvandlas en proton till en neutron och processen skapar en positron och en elektronneutrino. β ⁺ -sönderfall är också känt som positronemission .

Beta-sönderfall bevarar ett kvantantal som kallas leptonnumret , eller antalet elektroner och deras associerade neutriner (andra leptoner är muon- och tau -partiklarna). Dessa partiklar har leptonnummer +1, medan deras antipartiklar har leptonnummer −1. Eftersom en proton eller neutron har lepton nummer noll måste β ⁺ sönderfall (en positron eller antielektron) åtföljas av en elektronneutrino, medan β ⁻ sönderfall (en elektron) måste åtföljas av en elektron antineutrino.

Ett exempel på elektronemission (β ⁻ sönderfall) är sönderfallet av kol-14 till kväve-14 med en halveringstid på cirka 5 730 år:

¹⁴ ₆ C
→
¹⁴ ₇ N
+
e ⁻
+
ν
_e

I denna form av sönderfall blir det ursprungliga elementet ett nytt kemiskt element i en process som kallas nukleär transmutation . Detta nya grundämne har ett oförändrat massatal A , men ett atomnummer Z som ökas med ett. Som i alla nukleära sönderfall är det sönderfallande elementet (i detta fall
¹⁴ ₆ C
) känt som modernukliden medan det resulterande elementet (i detta fall
¹⁴ ₇ N
) är känt som dotternukliden .

Ett annat exempel är sönderfallet av väte-3 ( tritium ) till helium-3 med en halveringstid på cirka 12,3 år:

³ ₁ H
→
³ ₂ He
+
e ⁻
+
ν
_e

Ett exempel på positronemission (β ⁺ sönderfall) är sönderfallet av magnesium-23 till natrium-23 med en halveringstid på cirka 11,3 s:

²³ ₁₂ Mg
→
²³ ₁₁ Na
+
e ⁺
+
v
_e

β ⁺ sönderfall resulterar också i kärntransmutation, där det resulterande elementet har ett atomnummer som minskas med ett.

Ett betaspektrum som visar en typisk uppdelning av energi mellan elektron och antineutrino

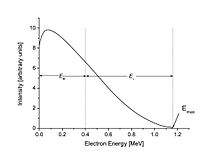
Betaspektrumet, eller fördelningen av energivärden för beta-partiklarna, är kontinuerlig. Den totala energin för sönderfallsprocessen är uppdelad mellan elektronen, antineutrino och rekylnukliden. I figuren till höger visas ett exempel på en elektron med 0,40 MeV energi från beta-avklingningen av ^{210 Bi.} I det här exemplet är den totala sönderfallsenergin 1,16 MeV, så antineutrino har den återstående energin: 1,16 MeV − 0,40 MeV = 0,76 MeV . En elektron längst till höger på kurvan skulle ha den maximala möjliga kinetiska energin, vilket gör att neutrinons energi bara är dess lilla vilomassa.

Historia

Upptäckt och initial karaktärisering

Radioaktivitet upptäcktes 1896 av Henri Becquerel i uran och observerades därefter av Marie och Pierre Curie i torium och i de nya elementen polonium och radium . 1899 Ernest Rutherford upp radioaktiva utsläpp i två typer: alfa och beta (nu beta minus), baserat på penetration av föremål och förmåga att orsaka jonisering. Alfastrålar kunde stoppas av tunna pappersark eller aluminium, medan beta-strålar kunde tränga igenom flera millimeter aluminium. År 1900 Paul Villard en ännu mer genomträngande typ av strålning, som Rutherford identifierade som en fundamentalt ny typ 1903 och kallade gammastrålar . Alfa, beta och gamma är de tre första bokstäverna i det grekiska alfabetet .

År 1900 mätte Becquerel mass-till-laddning-förhållandet ( m / e ) för beta-partiklar med JJ Thomsons metod som användes för att studera katodstrålar och identifiera elektronen. Han fann att m / e för en beta-partikel är densamma som för Thomsons elektron, och föreslog därför att beta-partikeln i själva verket är en elektron.

1901 visade Rutherford och Frederick Soddy att alfa- och beta-radioaktivitet involverar omvandling av atomer till atomer av andra kemiska element. År 1913, efter att produkterna från mer radioaktiva sönderfall var kända, föreslog Soddy och Kazimierz Fajans oberoende av varandra sin lag om radioaktivt förskjutning , som säger att beta-utsläpp (dvs.
β ⁻
) från ett grundämne producerar ett annat grundämne en plats till höger i det periodiska systemet , medan alfaemission producerar ett element två ställen till vänster.

Neutrinos

neutrinonets existens . I både alfa- och gammasönderfall har den resulterande alfa- eller gammapartikeln en smal energifördelning, eftersom partikeln bär energin från skillnaden mellan det initiala och slutliga kärntillståndet. Den kinetiska energifördelningen, eller spektrumet, av beta-partiklar uppmätt av Lise Meitner och Otto Hahn 1911 och av Jean Danysz 1913 visade dock flera linjer på en diffus bakgrund. Dessa mätningar gav det första tipset om att beta-partiklar har ett kontinuerligt spektrum. 1914 använde James Chadwick en magnetisk spektrometer med en av Hans Geigers nya räknare för att göra mer exakta mätningar som visade att spektrumet var kontinuerligt. Fördelningen av beta-partikelenergier var i uppenbar motsägelse till lagen om bevarande av energi . Om beta-sönderfall helt enkelt var elektronemission som antogs vid den tiden, borde energin hos den emitterade elektronen ha ett särskilt väldefinierat värde. För beta-sönderfall antydde emellertid den observerade breda fördelningen av energier att energi går förlorad i beta-sönderfallsprocessen. Detta spektrum var förbryllande i många år.

Ett andra problem är relaterat till bevarandet av rörelsemängd . Molekylära bandspektra visade att kärnspinnet för kväve-14 är 1 (dvs lika med den reducerade Planck-konstanten ) och mer generellt att spinnet är integral för kärnor med jämnt massatal och halvintegral för kärnor med udda masstal. Detta förklarades senare av proton-neutronmodellen av kärnan . Beta-sönderfall lämnar masstalet oförändrat, så förändringen av kärnspinn måste vara ett heltal. Elektronspinnet är dock 1/2, därför skulle vinkelmomentum inte bevaras om beta-sönderfall helt enkelt var elektronemission.

Från 1920 till 1927 fastställde Charles Drummond Ellis (tillsammans med Chadwick och kollegor) ytterligare att beta-sönderfallsspektrumet är kontinuerligt. År 1933 fick Ellis och Nevill Mott starka bevis för att betaspektrumet har en effektiv övre energigräns. Niels Bohr hade föreslagit att betaspektrumet skulle kunna förklaras om bevarande av energi endast var sant i statistisk mening, så denna princip kan kränkas i varje givet förfall. Den övre gränsen för betaenergier som bestämts av Ellis och Mott uteslöt dock den uppfattningen. Nu blev problemet med hur man redogör för variabiliteten av energi i kända beta-sönderfallsprodukter, såväl som för bevarande av momentum och vinkelmomentum i processen, akut.

I ett berömt brev skrivet 1930 försökte Wolfgang Pauli lösa beta-partikelenergiproblemet genom att föreslå att atomkärnor förutom elektroner och protoner också innehöll en extremt lätt neutral partikel, som han kallade neutronen. Han föreslog att denna "neutron" också sänds ut under beta-sönderfall (och står alltså för den kända saknade energin, rörelsemängden och rörelsemängden), men den hade helt enkelt inte observerats ännu. 1931 Enrico Fermi om Paulis "neutron" till "neutrino" ('lilla neutral en' på italienska). År 1933 publicerade Fermi sin landmärkesteori för beta-förfall , där han tillämpade kvantmekanikens principer på materiepartiklar, förutsatt att de kan skapas och förintas, precis som ljuskvantorna i atomära övergångar. Således, enligt Fermi, skapas neutriner i beta-sönderfallsprocessen, snarare än inneslutna i kärnan; samma sak händer med elektroner. Neutrinointeraktionen med materia var så svag att upptäckten av den visade sig vara en allvarlig experimentell utmaning. Ytterligare indirekta bevis på existensen av neutrinon erhölls genom att observera rekylen av kärnor som avgav en sådan partikel efter att ha absorberat en elektron. Neutrinos upptäcktes slutligen direkt 1956 av Clyde Cowan och Frederick Reines i Cowan-Reines neutrinoexperiment . Egenskaperna hos neutriner var (med några mindre modifieringar) som förutspåtts av Pauli och Fermi.

β ⁺
sönderfall och elektroninfångning

1934 bombarderade Frédéric och Irène Joliot-Curie aluminium med alfapartiklar för att åstadkomma kärnreaktionen
⁴ ₂ He
+
²⁷ ₁₃ Al
→
³⁰ ₁₅ P
+ ¹
₀ n
, och observerade att produktisotopen
³⁰ ₁₅ P
avger en funnen positron som är identisk med de i kosmiska strålar (upptäckt av Carl David Anderson 1932). Detta var det första exemplet på
β ⁺
sönderfall ( positronemission ), som de kallade artificiell radioaktivitet eftersom
³⁰ ₁₅ P
är en kortlivad nuklid som inte finns i naturen. Som ett erkännande av sin upptäckt tilldelades paret Nobelpriset i kemi 1935.

Teorin om elektronfångst diskuterades först av Gian-Carlo Wick i en artikel från 1934 och utvecklades sedan av Hideki Yukawa och andra. K-elektroninfångning observerades först 1937 av Luis Alvarez , i nukliden ⁴⁸ V. Alvarez fortsatte med att studera elektroninfångning i ⁶⁷ Ga och andra nuklider.

Icke-bevarande av paritet

1956 märkte Tsung-Dao Lee och Chen Ning Yang att det inte fanns några bevis för att paritet bevarades i svaga interaktioner, och därför postulerade de att denna symmetri kanske inte bevaras av den svaga kraften. De skissade designen för ett experiment för att testa bevarande av paritet i laboratoriet. Senare samma år Chien-Shiung Wu och kollegor Wu-experimentet som visade ett asymmetriskt beta-sönderfall av ⁶⁰
Co
vid kalla temperaturer som bevisade att paritet inte bevaras i beta-sönderfall. Detta överraskande resultat kullkastade sedan länge hållna antaganden om paritet och den svaga kraften. Som ett erkännande för sitt teoretiska arbete tilldelades Lee och Yang Nobelpriset i fysik 1957. Wu, som var kvinna, tilldelades dock inte Nobelpriset.

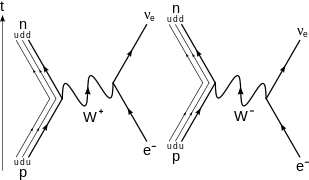
β ⁻ sönderfall

Den ledande ordningens Feynman-diagram för
β ⁻
sönderfall av en neutron till en proton , elektron och elektron antineutrino via en mellanliggande
W ⁻
boson . För diagram av högre ordning se

Vid
β ⁻
sönderfall omvandlar den svaga växelverkan en atomkärna till en kärna med atomnummer ökat med ett, samtidigt som det avger en elektron (
e ⁻
) och en elektron antineutrino (
ν
_e ).
β ⁻
sönderfall sker vanligtvis i neutronrika kärnor. Den generiska ekvationen är:

^A _Z X
→
^A _{Z +1} X′
+
e ⁻
+
ν
_e

där A och Z är masstalet och atomnumret för den sönderfallande kärnan, och X och X′ är de initiala respektive slutliga elementen.

Ett annat exempel är när den fria neutronen ( ¹
₀ n
) sönderfaller genom
β ⁻
sönderfall till en proton (
p
):

n
→
p
+
e ⁻
+
ν
_e .

På grundnivån (som visas i Feynman e ) - +2/3 e diagrammet till höger) orsakas detta av omvandlingen av den negativt laddade ( nedkvarken till − 1/3 den positivt laddade ( ) uppkvarken genom emission av en
W ⁻
boson ;
W ^-
bosonet sönderfaller därefter till en elektron och en elektron antineutrino:

d
→
u
+
e ⁻
+
ν
_e .

β ⁺ sönderfall

Huvudartikel: Positronemission

Feynmandiagrammet av ledande ordningen för
β ⁺
sönderfall av en proton till en neutron , positron och elektronneutrino via en mellanliggande
W ⁺
boson

Vid
β ⁺
-sönderfall, eller positronemission, omvandlar den svaga interaktionen en atomkärna till en kärna med atomnumret minskat med ett, samtidigt som det avger en positron (
e ⁺
) och en elektronneutrino (
ν
_e ).
β ⁺
-sönderfall sker vanligtvis i protonrika kärnor. Den generiska ekvationen är:

^A _Z X
→
^A _{Z −1} X′
+
e ⁺
+
ν
_e

Detta kan betraktas som sönderfallet av en proton inuti kärnan till en neutron:

p → n +
e ⁺
+
ν
_e

Däremot kan
β ⁺
-sönderfall inte inträffa i en isolerad proton eftersom det kräver energi, på grund av att neutronens massa är större än protonens massa.
β ⁺
sönderfall kan bara ske inuti kärnor när dotterkärnan har en större bindningsenergi (och därför en lägre total energi) än moderkärnan. Skillnaden mellan dessa energier går till reaktionen att omvandla en proton till en neutron, en positron och en neutrino och till den kinetiska energin hos dessa partiklar. Denna process är motsatsen till negativ beta-sönderfall, genom att den svaga interaktionen omvandlar en proton till en neutron genom att omvandla en upp-kvark till en ned-kvark, vilket resulterar i emission av ett W +
eller ^absorption
av ett
W ⁻
. När en
W ⁺
boson sönderfaller sönderfaller den till en positron och en elektronneutrino :

u
→
d
+
e ⁺
+
ν
_e .

Elektroninfångning (K-infångning)

Huvudartikel: Elektronfångning

De ledande Feynman-diagrammen för elektronfångstsönderfall . En elektron interagerar med en uppkvark i kärnan via en W-boson för att skapa en nedkvark och en elektronneutrino . Två diagram utgör den ledande (andra) ordningen, men som en virtuell partikel är typen (och laddningen) av W-boson omöjlig att skilja.

I alla fall där
β ⁺
sönderfall (positronemission) av en kärna tillåts energimässigt, så är elektroninfångning tillåten. Detta är en process under vilken en kärna fångar en av sina atomelektroner, vilket resulterar i utsläpp av en neutrino:

^A _Z X
+
e ⁻
→
^A _{Z −1} X′
+
ν
_e

Ett exempel på elektroninfångning är ett av sönderfallssätten för krypton-81 till brom-81 :

⁸¹ ₃₆ Kr
+
e ⁻
→
⁸¹ ₃₅ Br
+
ν
_e

Alla emitterade neutriner har samma energi. I protonrika kärnor där energiskillnaden mellan det initiala och slutliga tillståndet är mindre än 2 m _e c ^{2 är}
β ⁺
sönderfall inte energetiskt möjligt, och elektroninfångning är det enda sönderfallssättet.

Om den fångade elektronen kommer från atomens innersta skal, K-skalet , som har störst sannolikhet att interagera med kärnan, kallas processen K-infångning. Om det kommer från L-skalet kallas processen L-capture osv.

Elektroninfångning är en konkurrerande (samtidig) sönderfallsprocess för alla kärnor som kan genomgå β ⁺ sönderfall. Det omvända är dock inte sant: elektroninfångning är den enda typen av sönderfall som är tillåten i protonrika nuklider som inte har tillräcklig energi för att avge en positron och neutrino.

Nukleär transmutation

Diagram över isotoper efter typ av nukleärt sönderfall. Orange och blå nuklider är instabila, där de svarta rutorna mellan dessa regioner representerar stabila nuklider. Den obrutna linjen som passerar under många av nukliderne representerar den teoretiska positionen på grafen för nuklider för vilka protontalet är detsamma som neutrontalet. Grafen visar att element med fler än 20 protoner måste ha fler neutroner än protoner för att vara stabila.

Se även: Nukleär droppledning

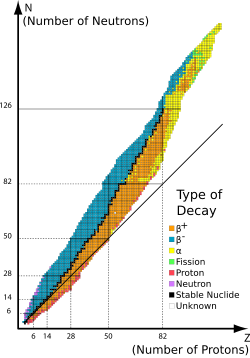
Om protonen och neutronen är en del av en atomkärna , omvandlar de ovan beskrivna sönderfallsprocesserna ett kemiskt element till ett annat. Till exempel:

137 55 Cs			→	137 56 Ba	+	e −	+	ν e	(beta minus förfall)
22 11 Na			→	22 10 Ne	+	e +	+	ν e	(beta plus förfall)
22 11 Na	+	e −	→	22 10 Ne	+	ν e			(elektroninfångning)

  Beta-sönderfall ändrar inte antalet ( A ) nukleoner i kärnan, utan ändrar endast dess laddning Z . Således kan uppsättningen av alla nuklider med samma A introduceras; dessa isobariska nuklider kan förvandlas till varandra via beta-sönderfall. För ett givet A finns det ett som är mest stabilt. Den sägs vara betastabil, eftersom den presenterar ett lokalt minimum av massöverskottet : om en sådan kärna har ( A , Z ) tal, har grannkärnorna ( A , Z −1) och ( A , Z +1) högre massöverskott och kan beta sönderfalla till ( A , Z ) , men inte vice versa. För alla udda massatal A finns det bara en känd beta-stabil isobar. För även A finns det upp till tre olika beta-stabila isobarer som experimentellt är kända; till exempel
¹²⁴ ₅₀ Sn
,
¹²⁴ ₅₂ Te
och
¹²⁴ ₅₄ Xe
alla betastabila. Det finns cirka 350 kända beta-sönderfallsstabila nuklider .

Konkurrens av beta-förfallstyper

Vanligtvis är instabila nuklider helt klart antingen "neutronrika" eller "protonrika", där de förra genomgår beta-sönderfall och de senare genomgår elektroninfångning (eller mer sällan, på grund av de högre energikraven, positronsönderfall). I ett fåtal fall av radionuklider med udda proton, udda neutron, kan det dock vara energetiskt gynnsamt för radionukliden att sönderfalla till en isobar med jämn proton, jämn neutron, antingen genom att genomgå beta-positiv eller beta-negativ sönderfall. Ett ofta nämnt exempel är den enskilda isotopen
⁶⁴ ₂₉ Cu
(29 protoner, 35 neutroner), som illustrerar tre typer av beta-sönderfall i konkurrens. Koppar-64 har en halveringstid på cirka 12,7 timmar. Denna isotop har en oparad proton och en oparad neutron, så antingen protonen eller neutronen kan sönderfalla. Denna speciella nuklid (även om inte alla nuklider i denna situation) är nästan lika sannolikt att sönderfalla genom protonsönderfall genom positronemission ( 18 % ) eller elektroninfångning ( 43% ) till
⁶⁴ ₂₈ Ni
, som det är genom neutronsönderfall genom elektronemission ( 39 % ) till
⁶⁴ ₃₀ Zn
.

Stabilitet av naturligt förekommande nuklider

De flesta naturligt förekommande nuklider på jorden är betastabila. Nuklider som inte är betastabila har halveringstider som sträcker sig från under en sekund till tidsperioder som är betydligt högre än universums ålder . Ett vanligt exempel på en långlivad isotop är udda-protonen udda-neutronnuklid
⁴⁰ ₁₉ K
, som genomgår alla tre typerna av beta-sönderfall (
β ⁻
,
β ⁺
och elektroninfångning) med en halveringstid på 1,277 × 10 ⁹ år .

Bevaranderegler för beta-förfall

Baryonnummer är bevarat

$$B={\frac {n_{q}-n_{\bar {q}}}{3}}$$

var

• $n_{q}$ är antalet ingående kvarkar, och
• $n_{\overline {q}}$ är antalet ingående antikvarkar.

Beta-sönderfall ändrar bara neutron till proton eller, i fallet med positiv beta-sönderfall ( elektroninfångning ) proton till neutron så att antalet individuella kvarkar inte ändras. Det är bara baryonsmaken som ändras, här betecknad som isospin .

Upp- och nedkvarkar har totalt isospin ${\textstyle I={\frac {1}{2}}}$ och isospinprojektioner

$$I_{\text{z}}={\begin{cases}{\frac {1}{2}}&{\text{up quark}} \\-{\frac {1}{2}}&{\text{down quark}}\end{cases}}$$

Alla andra kvarkar har I = 0 .

I allmänhet

$$I_{\text{z}}={\frac {1}{2}}(n_{\text{u}}-n_{\text{d }})$$

Leptonnumret är bevarat

$$L\equiv n_{\ell }-n_{\bar {\ell }}$$

så alla leptoner har tilldelat värdet +1, antileptoner −1 och icke-leptoniska partiklar 0.

$${\begin{matrix}&{\text{n}}&\rightarrow &{\text{p}}&+&{\ text{e}}^{-}&+&{\bar {\nu}}_{\text{e}}\\L:&0&=&0&+&1&-&1\end{matrix}}$$

Vinkelmoment

För tillåtna sönderfall är nettoomloppsrörelsemängden noll, därför beaktas endast spinnkvanttal.

Elektronen och antineutrino är fermioner , spin-1/2-objekt, därför kan de kopplas till totalt $S=1$ (parallell) eller $S=0$ (anti-parallell).

För förbjudna sönderfall måste också rörelsemängdsrörelsen beaktas.

Energifrigöring

Q - värdet definieras som den totala energi som frigörs vid ett givet kärnavfall. Vid beta-sönderfall Q därför också summan av de kinetiska energierna för den utsända beta-partikeln, neutrinon och rekylkärnan. (På grund av den stora massan av kärnan jämfört med beta-partikelns och neutrinon, kan den kinetiska energin hos den rekylerande kärnan i allmänhet försummas.) Betapartiklar kan därför emitteras med vilken kinetisk energi som helst som sträcker sig från kinetic energy ranging from 0 to Q. A typical Q is around 1 MeV, but can range from a few keV to a few tens of MeV.

Eftersom elektronens vilomassa är 511 keV, är de mest energirika beta-partiklarna ultrarelativistiska , med hastigheter mycket nära ljusets hastighet . I fallet med ¹⁸⁷ Re är beta-partikelns maximala hastighet endast 9,8 % av ljusets hastighet.

Följande tabell ger några exempel:

Exempel på beta-sönderfallsenergier

Isotop	Energi ( keV )	Förfallsläge	Kommentarer
gratis neutron	0782,33	β −
00 3 H (Tritium)	00 18,59	β −	Näst lägsta kända β −- energi, som används i KATRIN -experimentet.
0 11 C	0 960,4 1982,4	β + e +
0 14 C	0156,475	β −
0 20 F	5390,86	β −
0 37 K	5125.48 6147.48	β + e +
163 Ho	000 2,555	ε +
187 Re	000 2,467	β −	Lägsta kända β − energi, som används i mikrokalorimetermatriserna för ett Rheniumexperiment
210 Bi	1162,2	β −

β ⁻ sönderfall

Tänk på den generiska ekvationen för beta-förfall

^A _Z X
→
^A _{Z +1} X′
+
e ⁻
+
ν
_e .

Q - värdet för detta förfall är

$Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z }}+1}X'}}\right)-m_{e}-m_{{\overline {\nu}}_{e}}\right]c^{2}$ ,

där ${\displaystyle m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)} är massan$ av kärnan i atomen
^A _Z X ,
$m_{e}$ är elektronens massa, och $m_{{\overline {\nu }}_{e}}$ är massan av elektronen antineutrino. Med andra ord, den totala energin som frigörs är massenergin för den initiala kärnan, minus massenergin för den slutliga kärnan, elektronen och antineutrino. Massan av kärnan m _N är relaterad till standardatommassan m by

$$m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)c^{2}=m_{N}\left({\ce { ^{\mathit {A}}_{\mathit {Z}}X}}\right)c^{2}+Zm_{e}c^{2}-\sum _{i=1}^{Z} Bi}.$$

Det vill säga den totala atommassan är kärnans massa plus elektronernas massa minus summan av alla elektronbindande energier B _i för atomen. Denna ekvation arrangeras om för att hitta $m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)$ , och $m_{N}\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}} \right)$ hittas på liknande sätt. Genom att ersätta dessa kärnmassor i Q -värde-ekvationen, samtidigt som vi försummar antineutrinomassan på nästan noll och skillnaden i elektronbindningsenergier, som är mycket liten för hög- Z -atomer, har vi

$$Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}+1}X'}}\right)\right]c ^{2}$$

Denna energi förs bort som kinetisk energi av elektronen och antineutrino.

Eftersom reaktionen kommer att fortgå endast när Q- värdet är positivt, kan β ⁻ sönderfall inträffa när massan av atom
^A _Z X
är större än massan av atom
^A _{Z +1} X′
.

β ⁺ sönderfall

Ekvationerna för β ⁺ sönderfall är liknande, med den generiska ekvationen

^A _Z X
→
^A _{Z −1} X′
+
e ⁺
+
ν
_e

ger

$$Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m_{N}\left({ \ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-m_{e}-m_{\nu _{e}}\right]c^ {2}.$$

Men i denna ekvation upphävs inte elektronmassorna, och vi står kvar med

$$Q=\left[m\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)-m\left({\ce {^{\ mathit {A}}_{{\mathit {Z}}-1}X'}}\right)-2m_{e}\right]c^{2}.$$

Eftersom reaktionen kommer att fortgå endast när Q -värdet är positivt, kan β ⁺ sönderfall inträffa när massan av atomen
^A _Z X
överstiger den för
^A _{Z -1} X′
med minst två gånger massan av elektronen.

Elektroninfångning

Den analoga beräkningen för elektroninfångning måste ta hänsyn till elektronernas bindningsenergi. Detta beror på att atomen kommer att lämnas i ett exciterat tillstånd efter att ha fångat elektronen, och bindningsenergin för den fångade innersta elektronen är signifikant. Använder den generiska ekvationen för elektroninfångning

^A _Z X
+
e ⁻
→
^A _{Z −1} X′
+
ν
_e

vi har

$$Q=\left[m_{N}\left({\ce {^{\mathit {A}}_{\mathit {Z}}X}}\right)+m_{e}-m_{N}\left({\ce {^{\mathit {A}}_{ {\mathit {Z}}-1}X'}}\right)-m_{\nu _{e}}\right]c^{2},$$

vilket förenklar till

$$Q=\left[m\left({\ce {^{\mathit {A}} _{\mathit {Z}}X}}\right)-m\left({\ce {^{\mathit {A}}_{{\mathit {Z}}-1}X'}}\right) \right]c^{2}-B_{n},$$

där B _n är bindningsenergin för den fångade elektronen.

Eftersom elektronens bindningsenergi är mycket mindre än elektronens massa, kan kärnor som kan genomgå β ⁺ sönderfall alltid också genomgå elektroninfångning, men det omvända är inte sant.

Beta-emissionsspektrum

Betaspektrum på ²¹⁰ Bi. E _max = Q = 1,16 MeV är den maximala energin

Beta-förfall kan betraktas som en störning som beskrivs i kvantmekaniken, och därför kan Fermis gyllene regel tillämpas. Detta leder till ett uttryck för det kinetiska energispektrumet N ( T ) för emitterade betas enligt följande:

$$N(T)=C_{L}(T)F(Z,T)pE(QT)^ {2}$$

där T är den kinetiska energin, CL ₍ är en formfunktion som beror på sönderfallets förbjudenhet (den är konstant för tillåtna sönderfall), F Z , T ) är Fermifunktionen (se nedan) med Z laddningen av sluttillståndskärna, E = T + mc ² är den totala energin, $p={\sqrt {(E/c)^{2}-( mc)^{2}}}$ är momentum och Q är Q-värdet för avklingningen. Den kinetiska energin för den emitterade neutrinon ges ungefär av Q minus den kinetiska energin för beta.

Som ett exempel visas beta-sönderfallsspektrumet för ²¹⁰ Bi (ursprungligen kallat RaE) till höger.

Fermi funktion

Fermi-funktionen som visas i betaspektrumformeln står för Coulomb-attraktionen/avstötningen mellan den emitterade betan och sluttillståndskärnan. Genom att approximera de associerade vågfunktionerna till att vara sfäriskt symmetriska, kan Fermi-funktionen analytiskt beräknas vara:

$$F(Z,T)={\frac {2(1+S)}{\Gamma (1+2S)^{2}}}(2p\rho )^{2S-2}e^ {\pi \eta }|\Gamma (S+i\eta )|^{2},$$

där p är slutmomentet, Γ gammafunktionen och (om α är finstrukturkonstanten och r _N radien för sluttillståndskärnan) $S={\sqrt { 1-\alpha ^{2}Z^{2}}}$ , $\eta =\pm Ze^{2}c/\hbar p$ (+ för elektroner , − för positroner), och $\rho =r_{N}/\hbar$ .

För icke-relativistiska betaversioner ( Q ≪ m _e c ² ) kan detta uttryck approximeras med:

$$F(Z,T)\approx {\frac {2\pi \eta }{1-e^{-2\pi \eta }}}.$$

Andra uppskattningar finns i litteraturen.

Kurie tomt

En Kurie-plot (även känd som en Fermi–Kurie-plot ) är en graf som används för att studera beta-sönderfall utvecklad av Franz ND Kurie , där kvadratroten av antalet beta-partiklar vars momenta (eller energi) ligger inom ett visst smalt område , dividerat med Fermi-funktionen, plottas mot beta-partikelenergi. Det är en rak linje för tillåtna övergångar och vissa förbjudna övergångar, i enlighet med Fermi beta-förfallsteorin. Energiaxelns (x-axelns) skärning av en Kurie-plot motsvarar den maximala energin som tilldelas elektronen/positronen (avklingningens Q- värde). Med en Kurie-plot kan man hitta gränsen för den effektiva massan av en neutrino.

Helicitet (polarisation) av neutriner, elektroner och positroner som emitteras i beta-sönderfall

Efter upptäckten av paritetsicke-konservering (se Historia ), fann man att vid beta-sönderfall emitteras elektroner mestadels med negativ helicitet , dvs de rör sig, naivt sett, som vänsterhänta skruvar som drivs in i ett material (de har negativ longitudinell polarisation ). Omvänt har positroner mestadels positiv helicitet, dvs de rör sig som högerhänta skruvar. Neutriner (emitteras vid positronsönderfall) har negativ helicitet, medan antineutriner (emitteras vid elektronsönderfall) har positiv helicitet.

Ju högre energi partiklarna har, desto högre polarisering.

Typer av beta-sönderfallsövergångar

Huvudartikel: Beta decay transition

Beta-sönderfall kan klassificeras enligt vinkelmomentet ( L -värde ) och totalt spinn ( S- värde ) för den utsända strålningen. Eftersom total rörelsemängd måste bevaras, inklusive orbital och spin vinkelmomentum, inträffar beta-sönderfall genom en mängd olika kvanttillståndsövergångar till olika nukleära vinkelmoment eller spinntillstånd, kända som "Fermi" eller "Gamow–Teller" övergångar. När beta-sönderfallspartiklar inte har någon rörelsemängd ( L = 0 ), hänvisas sönderfallet till som "tillåtet", annars är det "förbjudet".

Andra sönderfallslägen, som är sällsynta, är kända som bunden tillståndssönderfall och dubbel beta-sönderfall.

Fermi övergångar

En Fermi-övergång är ett beta-sönderfall där spinnerna för den emitterade elektronen (positronen) och anti-neutrino (neutrino) kopplas till totalt spin $S=0$ , vilket leder till en vinkelmomentumändring ${\ displaystyle \Delta J=0}$ mellan kärnans initiala och slutliga tillstånd (förutsatt en tillåten övergång). I den icke-relativistiska gränsen ges den nukleära delen av operatören för en Fermi-övergång av

$${\mathcal {O}}_{F}=G_{V}\summa _{a}{\hat {\tau }}_{a\pm }$$

med $G_{V}$ den svaga vektorkopplingskonstanten, $\tau _{\pm }$ isospin - höjnings- och sänkoperatorerna och $a$ som löper över alla protoner och neutroner i kärnan.

Övergångar mellan Gamow och Teller

En Gamow–Teller-övergång är ett beta-sönderfall där spinnerna för den emitterade elektronen (positronen) och anti-neutrino (neutrino) kopplas till totalt spin $S=1$ , vilket leder till en vinkelmomentumändring $\Delta J=0,\pm 1$ mellan kärnans initiala och slutliga tillstånd (förutsatt en tillåten övergång). I detta fall är den nukleära delen av operatören given av

$$\displaystyle {\mathcal {O}}_{GT}=G_{A}\summa _{a}{\hat {\sigma }}_{ a}{\hat {\tau }}_{a\pm }}$$

med $G_{A}$ den svaga axialvektorkopplingskonstanten, och $\sigma$ spinn Pauli-matriserna , som kan producera en spin-flip i den sönderfallande nukleonen.

Förbjudna övergångar

När L > 0 hänvisas till som " förbjudet ". Nukleära urvalsregler kräver att höga L -värden åtföljs av förändringar i kärnspinn ( J ) och paritet ( π ). Urvalsreglerna för de L: te förbjudna övergångarna är:

$$\Delta J=L-1,L,L+1;\Delta \pi =(-1)^{L},$$

där Δ π = 1 eller −1 motsvarar ingen paritetsändring respektive paritetsändring. Det speciella fallet med en övergång mellan isobariska analoga tillstånd, där strukturen för det slutliga tillståndet är mycket lik strukturen för det initiala tillståndet, hänvisas till som "supertillåtet" för beta-sönderfall och fortskrider mycket snabbt. Följande tabell listar Δ J- och Δ π -värdena för de första värdena av L :

Förbud	Δ J	Δ π
Supertillåtet	0	Nej
Tillåten	0, 1	Nej
Först förbjudet	0, 1, 2	Ja
För det andra förbjudet	1, 2, 3	Nej
För det tredje förbjudet	2, 3, 4	Ja

Sällsynta förfallslägen

Bundet tillstånd β ⁻ sönderfall

En mycket liten minoritet av fria neutronsönderfall (cirka fyra per miljon) är så kallade "tvåkroppssönderfall", där protonen, elektronen och antineutrino produceras, men elektronen lyckas inte få den energi på 13,6 eV som krävs för att undkomma proton, och förblir därför helt enkelt bunden till den, som en neutral väteatom . I denna typ av beta-sönderfall bärs i huvudsak all neutronsönderfallsenergi bort av antineutrino.

För helt joniserade atomer (bara kärnor) är det på samma sätt möjligt för elektroner att misslyckas med att fly atomen och emitteras från kärnan till lågt liggande atombundna tillstånd (orbitaler). Detta kan inte inträffa för neutrala atomer med lågt bundna tillstånd som redan är fyllda av elektroner.

Bound-state β-sönderfall förutspåddes av Daudel , Jean och Lecoin 1947, och fenomenet i helt joniserade atomer observerades först för ¹⁶³ Dy ⁶⁶⁺ 1992 av Jung et al. från Darmstadt Heavy-Ion Research Center . Även om neutral ¹⁶³
Dy är en stabil isotop, genomgår den helt joniserade ¹⁶³ Dy ⁶⁶⁺ β-sönderfall i K- och L-skalen med en halveringstid på 47 dagar. Den resulterande kärnan - ¹⁶³
Ho - är stabil endast i det helt joniserade tillståndet och kommer att sönderfalla via elektroninfångning till ¹⁶³
Dy i neutralt tillstånd. Halveringstiden för den senare är 4750 år.

En annan möjlighet är att en helt joniserad atom genomgår kraftigt accelererad β-sönderfall, som observerats för ¹⁸⁷ Re av Bosch et al., också i Darmstadt. Neutral ¹⁸⁷ Re genomgår visserligen β-sönderfall med en halveringstid på 41,6 × 10 ⁹ år, men för fullt joniserad ¹⁸⁷ Re ⁷⁵⁺ förkortas denna till endast 32,9 år. Som jämförelse är variationen av sönderfallshastigheter för andra kärntekniska processer på grund av kemisk miljö mindre än 1 % . På grund av skillnaden i priset på rhenium och osmium och den höga andelen ¹⁸⁷
Re i rheniumprover som finns på jorden, kan detta en dag vara av kommersiellt intresse för syntesen av ädla metaller .

Dubbel beta-förfall

Huvudartikel: Dubbel beta-förfall

Vissa kärnor kan genomgå dubbel beta-sönderfall (ββ-sönderfall) där kärnans laddning ändras med två enheter. Dubbelt beta-sönderfall är svårt att studera, eftersom processen har en extremt lång halveringstid. I kärnor för vilka både β-sönderfall och ββ-sönderfall är möjligt, är den mer sällsynta ββ-sönderfallsprocessen i praktiken omöjlig att observera. Men i kärnor där β-sönderfall är förbjudet men ββ-sönderfall är tillåtet, kan processen ses och en halveringstid mätas. Således studeras ββ-sönderfall vanligtvis endast för beta-stabila kärnor. Precis som enkel beta-sönderfall ändrar inte dubbel beta-sönderfall A ; sålunda måste åtminstone en av nukliderna med något givet A vara stabil med avseende på både enkel och dubbel beta-sönderfall.

"Vanligt" dubbel beta-sönderfall resulterar i emission av två elektroner och två antineutriner. Om neutrinos är Majorana-partiklar (dvs de är deras egna antipartiklar), kommer ett sönderfall som kallas neutrinolöst dubbel beta-sönderfall att inträffa. De flesta neutrinofysiker tror att neutrinolöst dubbel beta-sönderfall aldrig har observerats.

Se även

• Vanliga beta-strålare
• Neutrino
• Betavoltaik
• Partikelstrålning
• Radionuklid
• Tritiumbelysning , en form av lysrörsbelysning som drivs av beta-sönderfall
• Pandemoniumeffekt
• Totalabsorptionsspektroskopi

Bibliografi

• Tomonaga, S.-I. (1997). Historien om Spin . University of Chicago Press .
• Tuli, JK (2011). Nuclear Wallet Cards (PDF) (8:e upplagan). Brookhaven National Laboratory . Arkiverad (PDF) från originalet 2022-10-09.

externa länkar

• The Live Chart of Nuclides - IAEA med filter på sönderfallstyp

• Beta-sönderfallssimulering [1]