Jämförelse av valsystem

Valsystem är reglerna för genomförande av val, vars huvudkomponent är algoritmen för att avgöra vinnaren (eller flera vinnare) från de avgivna rösterna. Den här artikeln diskuterar metoder och resultat för att jämföra olika valsystem, både de som väljer en unik kandidat i ett "envinnare"-val och de som väljer en grupp representanter i ett flervinnarval .

Olika valsystem kan bedömas med hjälp av expertutlåtanden , pragmatiska överväganden och kandidaturseffekter .

Dessutom finns det fyra huvudtyper av resonemang som har använts för att försöka bestämma den bästa röstningsmetoden:

1. Resultat av simulerade val
2. Överensstämmelse med logiska kriterier
3. Resultat av riktiga val
4. Argumentera med exempel .

System kan bedömas efter fördelar eller nackdelar med olika valsedelformat eller distriktsformat, oavsett om det är enmedlemsdistrikt eller flermedlemsdistrikt .

Expertutlåtanden om röstmetoder för en vinnare

Under 2010 tillfrågades en panel med 22 experter på röstningsförfaranden: "Vilken är den bästa röstregeln för din stad att använda för att välja borgmästare?". En ledamot avstod från att rösta. Godkännanderöstning användes för att välja mellan 18 röstningsmetoder för ensamvinnare. Rangordningen (med antal N godkännare från max 21) av de olika systemen var följande.

Notera: den här listan är inte representativ för alla tillgängliga röstmetoder för en vinnare, och flera av de inblandade experterna noterade senare brister i det sätt som omröstningen genomfördes. Arrangören av omröstningen argumenterar för att resultaten inte bör generaliseras, och hänvisar till det som en "naiv omröstning om röstningsregler".

Placera	Metod	N
1	Godkännande omröstning	15
2	Alternativ röst (IRV)	10
3	Copelands metod	9
4	Kemeny–Young metod	8
5	Två-runda system	6
5	Coombs metod	6
7	Minimax	5
7	Majoritetsdom	5
9	Borda räkna	4
10	Blacks metod	3
11	Rangröstning	2
11	Nansons metod	2
13	Leximin-metoden	1
13	Smiths metod	1
13	Otäckt uppsättningsmetod	1
16	Fishburns metod	–
16	Oinstängd set	–
16	FPTP	–

Pragmatiska överväganden

Ett intellektuellt problem som ställs av röstteorin är att utforma system som är korrekta i någon mening. Det finns dock också praktiska skäl till varför ett system kan vara mer socialt acceptabelt än ett annat.

De viktiga faktorerna kan grupperas under tre rubriker:

• Förståelighet , som Tideman definierar som "regelns förmåga att vinna väljarnas förtroende" och "beror på rimligheten och förståeligheten av regelns logik".
• Lätt att rösta . Olika former av valsedlar gör det mer eller mindre svårt för väljarna att fylla i valsedlar som på ett rättvist sätt återspeglar deras åsikter.
• Lätt att räkna . Röstsystem som fattar sina beslut från en liten uppsättning räkningar som härrör från röstsedlar är logistiskt sett mindre betungande än de som behöver konsultera hela uppsättningen av röstsedlar. Vissa röstningssystem kräver kraftfulla beräkningsresurser för att avgöra vinnaren. Även om kostnaden inte är oöverkomlig för användning vid val, kan det hindra en effektiv utvärdering.

Kandidateffekter

Ett separat ämne är det faktum att olika kandidater kan uppmuntras att kandidera till val under olika röstsystem. Rädslan för bortkastade röster under FPTP lägger mycket makt i händerna på de grupper som väljer ut kandidater. Ett annat röstsystem skulle kunna leda till mer tillfredsställande beslut utan att nödvändigtvis vara mer rättvist i någon abstrakt mening. Detta ämne har fått lite analytisk undersökning.

Ett kanadensiskt exempel på detta är kommunalvalet i London, Ontario 2018 . 2018, i avdelning 13, vann Arielle Kayabaga. Hennes framgång tillskrivs röstsystemet för omedelbar omröstning som precis tidigare hade ersatt staden Först förbi postsystemet, men egentligen skulle hon ha blivit vinnaren under Först förbi posten ändå. IRV kan göra anspråk på kredit för hennes framgång eftersom hon har sagt att hon inte skulle ha ställt upp om inte IRV ersatt FPTP.

Utvärdering genom simulering

Modeller av valprocessen

Röstningsmetoder kan utvärderas genom att mäta deras noggrannhet under slumpmässiga simulerade val som syftar till att vara trogna valens egenskaper i verkligheten. Den första sådan utvärderingen genomfördes av Chamberlin och Cohen 1978, som mätte frekvensen med vilken vissa icke-Condorcet-system valde Condorcet-vinnare. Det finns tre huvudtyper av modeller som har föreslagits som representationer av valprocessen, varav två kan kombineras i en hybrid. En fjärde typ av modell, den utilitaristiska modellen, är av begreppsmässig betydelse trots att den inte används i praktiken, även om rumsliga modeller ibland presenteras i utilitaristisk skepnad.

Condorcets jurymodell

Markisen de Condorcet såg ett val som analogt med en juryomröstning där varje medlem uttrycker en oberoende bedömning av kandidaternas kvalitet. Av detta skäl skiljer sig kandidaterna i objektiva meriter och väljarna uttrycker oberoende åsikter om kandidaternas relativa meriter. Så länge väljarnas bedömningar är bättre än slumpmässiga kommer alltid en tillräckligt stor väljarkår att välja den bästa kandidaten. En jurymodell är ibland känd som en valensmodell .

Jurymodellen innebär ett naturligt begrepp om noggrannhet för röstningssystem: ju mer sannolikt ett system är att välja den bästa kandidaten, desto bättre är systemet. Detta kan ses som en semantik för valbeslut.

Condorcet och hans samtida Laplace insåg att röstteori därmed kunde reduceras till sannolikhetsteori – Condorcets huvudverk fick titeln Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix . Deras idéer återupplivades under det tjugonde århundradet när det visades under en jurymodell att Kemeny-Young röstningsmetoden är den maximala sannolikhetsskattaren för ordningen av kandidater efter meriter.

Blacks rumsliga modell

Den främsta svagheten med Condorcets modell är dess antagande om oberoende: den antyder att det inte kan finnas någon tendens för väljare som föredrar A till B att också föredra C till D. Detta går emot bevis: någon som föredrar en viss montagnard framför en viss girondin kommer förmodligen också att föredra en andra montagnard framför en andra girondin ; det förklarar också varför även godtyckligt stora juryer är felbara, eftersom medlemmar kommer att göra vanliga misstag.

Duncan Black föreslog en endimensionell rumslig modell för röstning 1948, och såg val som ideologiskt styrda. Hans idéer utökades senare av Anthony Downs. Väljarnas åsikter betraktas som positioner i ett utrymme av en eller flera dimensioner; kandidater har positioner i samma utrymme; och väljarna väljer kandidater i ordning efter närhet (mätt under euklidiskt avstånd eller någon annan metrik).

Rumsliga modeller innebär en annan uppfattning om meriter för röstningssystem: ju mer acceptabel den vinnande kandidaten kan vara som en platsparameter för väljarfördelningen, desto bättre system. Ett politiskt spektrum är en endimensionell rumslig modell.

Arrows neutrala modell

Kenneth Arrow arbetade inom en ram där valsedlarna är den ultimata verkligheten snarare än att vara "meddelanden" (som Balinski och Laraki uttryckte det) som förmedlar partiell (och möjligen missvisande) information om någon verklighet bakom dem. Han föreslog inte denna agnosticism som en realistisk bild av röstning, utan snarare som att definiera val som matematiska objekt vars egenskaper kunde undersökas. Hans berömda omöjlighetsteorem visar (under vissa antaganden) att det för alla rankade röstningssystem finns uppsättningar av röstsedlar (som kan erhållas under en neutral modell) som bryter mot minst ett av tre kriterier som ofta anses vara önskvärda.

En neutral modell för inte med sig något begrepp om noggrannhet eller sanning för röstsystem.

Opartiska kulturmodeller definierar fördelningen av röstsedlar enligt en neutral röstningsmodell, och behandlar väljarna som en slumpmässig bullerkälla.

Hybridmodeller

Det är möjligt att kombinera jurymodeller med rumsliga modeller: man kan anta att väljarna påverkas dels av sin syn på kandidaternas kvaliteter och dels av ideologiska överväganden. Detta bryter ner deras preferenser i separata oberoende och icke-oberoende komponenter. Hybridmodeller diskuteras kort av Darlington men har inte antagits i stor utsträckning.

Empirisk jämförelse

Tideman och Plassmann genomförde en studie som visade att en tvådimensionell rumslig modell gav en rimlig anpassning till 3-kandidatminskningar av en stor uppsättning valrankningar. Jurymodeller och neutrala modeller och endimensionella rumsliga modeller visades vara otillräckliga men hybridmodeller övervägdes inte.

De tittade på Condorcets cykler i väljarpreferenser (ett exempel på vilket är att A föredras framför B av en majoritet av väljarna, B till C och C till A) och fann att antalet av dem överensstämde med effekter med små urval, och drog slutsatsen att "röstningscykler kommer att inträffa mycket sällan, om alls, i val med många väljare".

Relevansen av urvalsstorlek hade studerats tidigare av Gordon Tullock , som grafiskt hävdade att även om ändliga väljare alltid kommer att vara benägna att cykla, blir området där kandidater kan ge upphov till cykling successivt mindre när antalet väljare ökar.

Utilitaristiska modeller

En utilitaristisk modell ser väljarna som rangordnade kandidater i nyttoordning. Den rättmätige vinnaren, enligt denna modell, är den kandidat som maximerar den totala sociala nyttan. En utilitaristisk modell skiljer sig från en rumslig modell på flera viktiga sätt:

• Det kräver ytterligare antagandet att väljarna motiveras enbart av informerat egenintresse, utan någon ideologisk fläck av deras preferenser.
• Det kräver att avståndsmåttet för en rumslig modell ersätts av ett troget mått på användbarhet.
• Följaktligen kommer måttet att skilja sig åt mellan väljarna. Det händer ofta att en väljargrupp kommer att påverkas kraftigt av valet mellan två kandidater medan en annan grupp har lite på spel; måttet måste då vara mycket asymmetriskt.

Av den sista egenskapen följer att inget röstsystem som ger lika inflytande för alla väljare sannolikt kommer att uppnå maximal social nytta. Extrema fall av konflikt mellan påståenden om utilitarism och demokrati kallas " majoritetens tyranni" . Se Lasliers, Merlins och Nurmis kommentarer i Lasliers artikel.

James Mill tycks ha varit den första att hävda existensen av ett a priori samband mellan demokrati och utilitarism – se Stanford Encyclopedia-artikeln och Macaulays "berömda attack".

Jämförelser under jurymodell

Antag att den i: ^e   kandidaten i ett val har meriter x _i (vi kan anta att x _i ~ N (0,σ ² )), och att väljarens j :s godkännandenivå för kandidat i kan skrivas som x _i + ε _ij (vi kommer att anta att ε _ij är iid. N (0,τ ² )). Vi antar att en väljare rangordnar kandidater i fallande godkännandeordning. Vi kan tolka ε _ij som felet i väljare j :s värdering av kandidat i och betrakta en omröstningsmetod som har till uppgift att hitta den kandidat som har störst merit.

Varje väljare kommer att ranka den bästa av två kandidater högre än den mindre bra med en bestämd sannolikhet p (som enligt den normala modellen som beskrivs här är lika med ${\displaystyle {\tfrac {1}{ 2}}\!+\!{\tfrac {1}{\pi }}{\textrm {tan}}^{-1}{\tfrac {\sigma }{\tau }}}, vilket kan bekräftas$ från en standardformel för Gaussiska integraler över en kvadrant). Condorcets jurysats visar att så länge som p > 1 ⁄ 2 kommer majoriteten av en jury att vara en bättre vägledning för två kandidaters relativa meriter än någon enskild ledamots åsikt.

Peyton Young visade att ytterligare tre egenskaper gäller för röster mellan godtyckliga antal kandidater, vilket tyder på att Condorcet var medveten om den första och tredje av dem.

• Om p är nära 1 ⁄ 2 så är Borda- vinnaren den maximala sannolikhetsskattaren för den bästa kandidaten.
• om p är nära 1, är Minimax- vinnaren den maximala sannolikhetsskattaren för den bästa kandidaten.
• För varje p är Kemeny -Young-rankingen den maximala sannolikhetsskattaren för den verkliga meritordningen.

Robert F. Bordley konstruerade en "utilitaristisk" modell som är en liten variant av Condorcets jurymodell. Han såg uppgiften med en röstningsmetod som att hitta den kandidat som har det största totala godkännandet från väljarna, det vill säga den högsta summan av enskilda väljares godkännande. Denna modell är vettig även med σ ² = 0, i vilket fall p tar värdet ${\tfrac {1}{2}}\!+\!{\ tfrac {1}{\pi }}{\textrm {tan}}^{-1}{\tfrac {1}{n-1}}$ där n är antalet väljare. Han utförde en utvärdering enligt denna modell och fann som förväntat att Borda-räkningen var mest exakt.

Simulerade val under rumsliga modeller

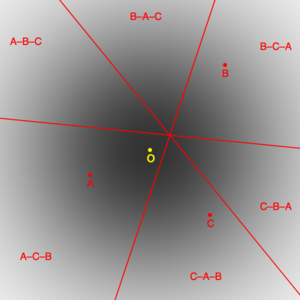
Ett simulerat val kan konstrueras från en fördelning av väljare i ett lämpligt utrymme. Illustrationen visar väljare som uppfyller en tvåvariabel Gauss-fördelning centrerad på O. Det finns 3 slumpmässigt genererade kandidater, A, B och C. Utrymmet är uppdelat i 6 segment med 3 rader, där väljarna i varje segment har samma kandidatpreferenser. Andelen väljare som beställer kandidaterna på något sätt ges av integralen av väljarfördelningen över det tillhörande segmentet.

De proportioner som motsvarar de 6 möjliga sorteringarna av kandidater bestämmer resultatet av olika röstningssystem. De som väljer den bästa kandidaten, det vill säga den kandidat som ligger närmast O (som i detta fall är A), anses ha gett ett korrekt resultat och de som väljer någon annan har uppvisat ett fel. Genom att titta på resultat för ett stort antal slumpmässigt genererade kandidater kan röstsystemens empiriska egenskaper mätas.

Utvärderingsprotokollet som beskrivs här är modellerat på det som beskrivits av Tideman och Plassmann. Utvärderingar av denna typ är vanligast för valsystem med ensam vinnare. Rangordnade röstningssystem passar mest naturligt in i ramverket, men andra typer av röstsedlar (såsom FPTP och Approval voting ) kan tillgodoses med mindre eller större ansträngning.

Utvärderingsprotokollet kan varieras på flera sätt:

• Antalet väljare kan göras ändligt och varieras i storlek. I praktiken görs detta nästan alltid i multivariata modeller, där väljarna provtas från deras fördelning och resultaten för stora väljare används för att visa begränsande beteende.
• Antalet kandidater kan varieras.
• Väljarfördelningen kunde varieras; till exempel kan effekten av asymmetriska fördelningar undersökas. En mindre avvikelse från normaliteten medförs av stickprovseffekter när antalet väljare är ändligt. Mer systematiska avvikelser (som verkar ha formen av en Gaussisk blandningsmodell ) undersöktes av Jameson Quinn 2017.

Utvärdering för noggrannhet

m metod	3	6	10	15	25	40
FPTP	70,6	35,5	21.1	14.5	9.3	6.4
AV/IRV	85,2	50,1	31,5	21.6	12.9	7.9
Borda	87,6	82,1	74,2	67,0	58,3	50,1
Condorcet	100,0	100,0	100,0	100,0	100,0	100,0

En av de viktigaste användningsområdena för utvärderingar är att jämföra röstsystemens noggrannhet när väljarna röstar uppriktigt. Om ett oändligt antal väljare uppfyller en gaussisk fördelning, kan den rättmätige vinnaren av ett val anses vara den kandidat som ligger närmast medelvärdet/medianen, och noggrannheten av en metod kan identifieras med andelen val där den rättmätige vinnaren utses. Medianväljarteoremet garanterar att alla Condorcet-system ger 100% noggrannhet (och detsamma gäller för Coombs metod ) .

Utvärderingar publicerade i forskningsartiklar använder flerdimensionella Gausser, vilket gör beräkningen numeriskt svår. Antalet väljare hålls begränsat och antalet kandidater är nödvändigtvis litet.

Beräkningen är mycket mer okomplicerad i en enda dimension, vilket tillåter ett oändligt antal väljare och ett godtyckligt antal m kandidater. Resultaten för detta enkla fall visas i den första tabellen, som är direkt jämförbar med Tabell 5 (1000 väljare, medelstor spridning) i den citerade artikeln av Chamberlin och Cohen. Kandidaterna provades slumpmässigt från väljarfördelningen och en enda Condorcet-metod ( Minimax ) inkluderades i försöken för bekräftelse.

m metod	10
FPTP	0,166
AV/IRV	0,058
Borda	0,016
Condorcet	0,010

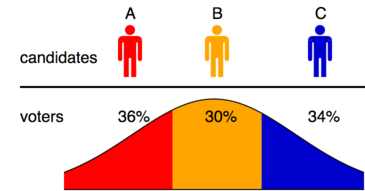
Det relativt dåliga resultatet för den alternativa rösten (IRV) förklaras av den välkända och vanliga felkällan som illustreras av diagrammet, där valet uppfyller en univariat rumslig modell och den rättmätige vinnaren B kommer att elimineras i den första omgången. Ett liknande problem finns i alla dimensioner.

Ett alternativt mått på noggrannhet är väljarnas genomsnittliga avstånd från vinnaren (där mindre betyder bättre). Detta kommer sannolikt inte att ändra rankningen av röstningsmetoder, men föredras av personer som tolkar avstånd som obrukbarhet. Den andra tabellen visar medelavståndet (i standardavvikelser) minus ${\displaystyle {\sqrt {\tfrac {2}{\pi }}}} ($ vilket är medelavståndet för en variat från mitten av en standard gaussisk distribution) för 10 kandidater enligt samma modell.

Utvärdering för motstånd mot taktisk omröstning

James Green-Armytage et al. publicerade en studie där de bedömde flera röstsystems sårbarhet för manipulation av väljarna. De säger lite om hur de anpassade sin utvärdering för detta ändamål, utan nämner helt enkelt att det "kräver kreativ programmering". En tidigare artikel av den första författaren ger lite mer detaljer.

Antalet kandidater i deras simulerade val var begränsat till 3. Detta tar bort skillnaden mellan vissa system; till exempel Blacks metod och Dasgupta-Maskin-metoden likvärdiga på 3 kandidater.

Slutsatserna från studien är svåra att sammanfatta, men Borda-räkningen fungerade dåligt; Minimax var något sårbart; och IRV var mycket resistent. Författarna visade att en begränsning av vilken metod som helst till val utan Condorcet-vinnare (att välja Condorcet-vinnare när det fanns en) aldrig skulle öka dess känslighet för taktisk omröstning. De rapporterade att "Condorcet-Hare"-systemet som använder IRV som tie-break för val som inte lösts av Condorcet-kriteriet var lika motståndskraftigt mot taktisk röstning som IRV i sig och mer exakt. Condorcet-Hare motsvarar Copelands metod med IRV-tie-break i val med 3 kandidater.

Utvärdering för effekten av kandidatfördelningen

x m	0	0,25	0,5	1	1.5
3	87,6	87,9	88,9	93,0	97,4
6	82,1	80,2	76,2	71,9	79,9
10	74,1	70,1	61,2	47,6	54,1
15	66,9	60,6	46,4	26.6	30.8
25	58,3	47,0	26.3	8.1	10.1
40	50,2	33.3	11.3	1.5	2.1

Vissa system, och Borda-antalet i synnerhet, är sårbara när fördelningen av kandidater förskjuts i förhållande till fördelningen av väljare. Den bifogade tabellen visar noggrannheten av Borda-räkningen (i procent) när en oändlig population av väljare uppfyller en univariat Gauss-fördelning och m kandidater dras från en liknande fördelning, kompenserad av x standardfördelningar. Röd färg indikerar siffror som är värre än slumpmässiga. Kom ihåg att alla Condorcet-metoder ger 100% noggrannhet för detta problem. (Och notera att minskningen i noggrannhet när x ökar inte syns när det bara finns 3 kandidater.)

Känslighet för fördelningen av kandidater kan ses som en fråga om antingen noggrannhet eller om motstånd mot manipulation. Om man förväntar sig att kandidaterna under saker och ting kommer naturligt att komma från samma fördelning som väljarna, så kommer varje förskjutning att ses som försök till subversion; men om man tror att faktorer som avgör kandidaturers lönsamhet (såsom ekonomiskt stöd) kan vara korrelerade med ideologisk position, då kommer man att se det mer i termer av noggrannhet.

Publicerade utvärderingar har olika syn på kandidatfördelningen. Vissa utgår helt enkelt från att kandidater dras från samma fördelning som väljarna. Flera äldre tidningar antar lika medel men låter kandidatfördelningen vara mer eller mindre stram än väljarfördelningen. En artikel av Tideman och Plassmann approximerar förhållandet mellan kandidat- och väljarfördelningar baserat på empiriska mätningar. Detta är mindre realistiskt än det kan tyckas, eftersom det inte tar hänsyn till att kandidatfördelningen anpassas för att utnyttja eventuella svagheter i röstsystemet. En artikel av James Green-Armytage ser på kandidatfördelningen som en separat fråga, och ser den som en form av manipulation och mäter effekterna av strategiskt inträde och utträde. Inte överraskande tycker han att Borda-greven är särskilt sårbar.

Värdering för övriga fastigheter

• Som tidigare nämnts mätte Chamberlin och Cohen med vilken frekvens vissa icke-Condorcet-system utser Condorcet-vinnare. Under en rumslig modell med lika väljar- och kandidatfördelningar är frekvenserna 99 % ( Coombs ), 86 % (Borda), 60 % (IRV) och 33 % (FPTP). Detta kallas ibland Condorcet effektivitet .
• Darlington mätte med vilken frekvens Copelands metod ger en unik vinnare i val utan Condorcet-vinnare. Han fann att det var mindre än 50 % för fält med upp till 10 kandidater.

Experimentell statistik

Uppgiften för ett röstsystem enligt en rumslig modell är att identifiera den kandidat vars position bäst representerar fördelningen av väljarnas åsikter. Detta innebär att man väljer en platsparameter för fördelningen från den uppsättning alternativ som erbjuds av kandidaterna. Platsparametrar kan baseras på medelvärdet, medianen eller moden; men eftersom rankade valsedlar endast ger ordningsinformation, är medianen den enda acceptabla statistiken.

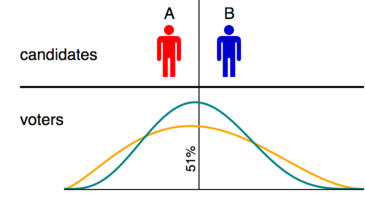
Detta framgår av diagrammet som illustrerar två simulerade val med samma kandidater men olika väljarfördelningar. I båda fallen är mittpunkten mellan kandidaterna den 51:a percentilen av väljarfördelningen; därför föredrar 51 % av väljarna A och 49 % föredrar B. Om vi ​​anser att en röstningsmetod är korrekt om den väljer den kandidat som ligger närmast medianen av väljarpopulationen, då medianen nödvändigtvis ligger något till vänster om 51 %. linje, kommer en röstningsmetod att anses vara korrekt om den väljer A i varje enskilt fall.

Medelvärdet av krickan-fördelningen är också något till vänster om 51%-linjen, men medelvärdet för orangefördelningen är något till höger. Om vi ​​därför anser att en röstningsmetod är korrekt om den väljer den kandidat som ligger närmast medeltalet av väljarpopulationen, så kommer en metod inte att kunna få full poäng om den inte ger olika vinnare från samma valsedlar i de två valen. Detta kommer uppenbarligen att tillskriva falska fel till röstningsmetoderna. Samma problem kommer att uppstå för alla kardinalmått på plats; endast medianen ger konsekventa resultat.

Medianen är inte definierad för multivariata distributioner men den univariata medianen har en egenskap som generaliserar bekvämt. Medianen för en fördelning är den position vars medelavstånd från alla punkter inom fördelningen är minst. Denna definition generaliserar till den geometriska medianen i flera dimensioner. Avståndet beskrivs ibland som en väljares "disanvändbarhet" från en kandidats val, men denna identifiering är rent godtycklig.

Om vi ​​har en uppsättning kandidater och en befolkning av väljare, då är det inte nödvändigt att lösa det beräkningsmässigt svåra problemet att hitta den geometriska medianen för väljarna och sedan identifiera den kandidat som ligger närmast den; istället kan vi identifiera den kandidat vars genomsnittliga avstånd från väljarna är minimerat. Detta är det mått som allmänt har använts sedan Merrill och framåt; se även Green-Armytage och Darlington.

Den kandidat som ligger närmast den geometriska medianen av väljarfördelningen kan betecknas som "rumslig vinnare".

Utvärdering genom verkliga val

Data från verkliga val kan analyseras för att jämföra effekterna av olika system, antingen genom att jämföra mellan länder eller genom att tillämpa alternativa valsystem på de verkliga valdata.

Möjlighet till en sådan bedömning uppstår när valsystemen ändras.

Ett kanadensiskt exempel på en sådan möjlighet finns i staden Edmonton (Kanada), som gick från att rösta först efter att ha röstat i Alberta 1917 till att rösta i pluralitetsblock med fem medlemmar i 1921 års allmänna val i Alberta till fem- medlem Singel överförbar röstning i 1926 Alberta riksdagsval , sedan till First-förbi-posta röstning igen i 1959 Alberta riksdagsval . Ett parti sopade alla Edmonton-platserna 1917, 1921 och 1959. Under STV 1926 valdes två konservativa, en liberal, en Labour och en United Farmers MLA.

Argumentera med exempel

Antal väljare	Ranking
30	ABC
1	ACB
29	BAC
10	BCA
10	CAB
1	CBA

Det finns en lång historia av att försöka bevisa överlägsenheten hos en röstningsmetod framför en annan genom att konstruera exempel där de två metoderna ger olika svar, det hävdas triumferande att den första metoden är rätt och den andra fel. Eftersom exempel kan konstrueras som är ofördelaktiga för alla metoder, kan denna form av resonemang vara ofullständig. Ett exempel förekommer ovan där vi illustrerar en svaghet i IRV med hjälp av ett fiktivt val där den rättmätige vinnaren skulle elimineras.

En nyligen uppmärksammad instans har getts av Donald Saari . Han analyserade om ett exempel från Condorcet på ett hypotetiskt val mellan 3 kandidater med 81 väljare vars preferenser är som visas i den första tabellen.

den initiala räkningen med bara första preferenser skulle vara A 31, B 39, C 11

Först förbi posten skulle välja B med 39 röster, mindre än hälften av rösterna.

IRV skulle se C elimineras i 2:a steget, vilket resulterar i nya räkningar: A 41, B 40. De flesta skulle säga att A, som är första- eller andravalet av fler väljare än B, är den rättmätige vinnaren.

Vinnaren av Condorcet är A, som föredras framför B vid 41:40 och framför C med 60:21; men Borda-vinnaren är B. Condorcet drog slutsatsen att Borda-räkningen var fel. Saari hävdar att Borda-räkningen har rätt i det här fallet, och noterar att väljarna kan delas upp i 3 grupper som visas av den andra tabellen.

Antal väljare	Ranking
10	ABC
10	BCA
10	CAB
1	ACB
1	CBA
1	BAC
20	ABC
28	BAC

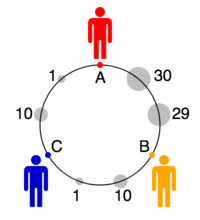
De rosa och blå grupperna består av medurs och moturs cykler som – enligt Saari – tar bort sig själva och lämnar resultatet att bestämmas av den vita gruppen; och den här gruppens tydliga preferens (igen enligt Saari) är B.

Diagrammet visar en möjlig konfiguration av väljarna och kandidaterna i enlighet med valsedlarna, med alla placerade på omkretsen av en enhetscirkel. Det bekräftar Saaris bedömning genom att A:s avstånd från den genomsnittliga väljaren är 1,15 medan B:s är 1,09 (och C:s är 1,70), vilket gör B till den rumsliga vinnaren. Men det är bara ett exempel. Vi kan tänka oss att hålla alla positioner fasta utom A och flytta A radiellt mot cirkelns mitt. Ett oändligt litet steg räcker för att göra A till preferens för de cykliska grupperna, även om den vita gruppen fortsätter att föredra B. När A:s avstånd från centrum är mindre än cirka 0,89 växlar den övergripande preferensen från B till A, även om röstsedlarna skulle vara oförändrad.

Således är valet tvetydigt i det att lika rimliga rumsliga representationer innebär olika vinnare. Detta är den tvetydighet vi försökte undvika tidigare genom att anta ett medianmått för rumsliga modeller; men även om medianmåttet uppnår sitt mål i en enda dimension och generaliserar attraktivt till högre dimensioner, generaliserar inte egenskapen som behövs för att undvika tvetydighet. I allmänhet kan cykler göra den rumsliga vinnaren obestämd utan hänvisning till externa fakta. Förekomsten av en rundstrålande väljarmedian är ett tillräckligt villkor för att säkerställa ett bestämt resultat från de avgivna rösterna, och i detta fall är den rumsliga vinnaren Condorcet-vinnaren; och endimensionalitet av väljarfördelningen är tillräcklig för att den ska ha en rundstrålande median.

Saaris exempel har varit inflytelserik. Darlington berättar att han fick höra av en "recensent för en mycket prestigefylld akademisk tidskrift" att ett liknande exempel visar att Condorcet-kriteriet är "löjligt, eftersom en uppsättning röster som visar oavgjort inte borde ändra ett valresultat".

Logiska kriterier för val med ensam vinnare

Traditionellt har fördelarna med olika valsystem argumenterats med hänvisning till logiska kriterier. Dessa har formen av slutledningsregler för valbeslut, som ger tillstånd för avdraget, till exempel att "om E och E ' är val sådana att R ( E , E '), och om A är den rättmätige vinnaren av E , då A är den rättmätige vinnaren av E ' ".

Kriterierna är lika diskutabla som själva röstsystemen. Här diskuterar vi kortfattat de överväganden som framförts angående deras giltighet, och sammanfattar sedan de viktigaste kriterierna och visar i en tabell vilka av de huvudsakliga röstsystemen som uppfyller dem.

Epistemologi av röstkriterier

Argument från exempel

Ett exempel på felaktigt uppträdande i ett röstningssystem kan generaliseras till att ge ett kriterium som garanterar att inget sådant fel kan uppstå från ett system som uppfyller kriteriet, även i mer komplicerade fall. Saaris exempel ger avbokningskriteriet (som uppfylls av Borda-räkningen men överträds av alla Condorcet-system); exemplet som illustreras av IRV som eliminerar den rättmätige vinnaren kan generaliseras som Condorcet-kriteriet (som bryts av Borda-räkningen).

En mer intressant generalisering kommer från den klass av exempel som kallas "no-show-paradoxer" som kan illustreras från samma diagram. Genom att hålla med om att B är den rättmätige vinnaren kan vi anta att under ett visst röstningssystem kommer B verkligen att väljas om alla väljare röstar uppriktigt, men att enligt detta system kan en enskild anhängare av A luta resultatet mot sin föredragna kandidat genom att helt enkelt avstå från att rösta . De flesta skulle hålla med om att detta skulle vara ett absurt resultat. Om vi ​​fäste vikt vid det skulle vi kunna generalisera det till deltagandekriteriet , som säger att en väljare aldrig kan hjälpa en kandidat mer genom att avstå än genom att rösta.

Det är ett stort steg från exemplet till kriteriet. I exemplet är det paradoxala resultatet helt enkelt fel: B förblir den rättmätige vinnaren när en anhängare av A avstår. Men när vi antar deltagandekriteriet begränsar vi valresultaten i komplicerade exempel där det är omöjligt att identifiera den rättmätige vinnaren och med konsekvenser som är svåra att förutse; det här kan vara mer än vad vi hade räknat med.

Deltagandekriteriet visar sig vara förvånansvärt kraftfullt: det avvisar alla Condorcet-system samtidigt som det accepterar Borda-räkningen. Men de no-show-paradoxer som uppstår från Condorcet-system är aldrig exempel där resultaten helt enkelt är felaktiga, utan snarare fall där resultatpar är relaterade på ett oönskat sätt utan att vara bestämt rätt eller fel.

Logisk konsekvens

De allmänt accepterade kriterierna är ömsesidigt inkonsekventa i olika grupper (den första av dem är gruppen av 3 inkompatibla kriterier som identifieras av Arrows omöjlighetsteorem ). De strider också mot alla röstsystem. Dan Felsenthal beskrev 16 kriterier och 18 röstsystem och visade "att vart och ett av hans 18 system bryter mot minst sex av dessa kriterier".

Resultatkriterier (absolut)

Vi övergår nu till själva de logiska kriterierna, och börjar med de absoluta kriterierna som säger att om valsedlarna är på ett visst sätt, måste eller inte får en viss kandidat vinna.

Majoritetskriterium (MC)

Kommer alltid en kandidat att vinna som rankas som den unika favoriten av en majoritet av väljarna? Detta kriterium finns i två versioner:

1. Rangordnad majoritetskriterium, där ett alternativ som bara föredras framför de andra av en majoritet måste vinna. (Att godkänna den rankade MC betecknas med " ja " i tabellen nedan, eftersom det också innebär att man klarar följande:)
2. Bedömd majoritetskriterium, där endast ett alternativ som unikt ges ett perfekt betyg av en majoritet måste vinna. De rankade och rankade MC är synonyma för rankade röstningsmetoder, men inte för rankade eller graderade. Den rankade MC, men inte den rankade MC, är inkompatibel med IIA-kriteriet som förklaras nedan.

Ömsesidig majoritetskriterium (MMC)

Kommer alltid en kandidat att vinna som är bland en grupp kandidater som rankas över alla andra av en majoritet av väljarna? Detta innebär också majoritetsförlorarkriteriet – om en majoritet av väljarna föredrar varannan kandidat framför en given kandidat, vinner då inte den kandidaten? Därför, av de listade metoderna, klarar alla varken eller båda kriterierna, förutom Borda, som klarar Majority Loser medan den inte klarar ömsesidig majoritet.

Condorcet-kriterium

Kommer alltid en kandidat att vinna som slår varannan kandidat i parvisa jämförelser? (Detta innebär majoritetskriteriet ovan.)

Condorcet förlorare kriterium (kond. förlorare)

Kommer en kandidat aldrig att vinna som förlorar mot varannan kandidat i parvisa jämförelser?

Resultatkriterier (relativt)

Dessa är kriterier som säger att om en viss kandidat vinner under en omständighet, måste (eller inte får) samma kandidat vinna i en relaterad omständighet.

Oberoende av Smith-dominerade alternativ (ISDA)

Förändras aldrig utfallet om en Smith -dominerad kandidat läggs till eller tas bort (förutsatt att rösterna för de andra kandidaterna är oförändrade)? Kandidat C är Smith-dominerad om det finns någon annan kandidat A så att C blir slagen av A och varje kandidat B som inte blir slagen av A etc. Observera att även om detta kriterium klassas här som nominerad-relativt, har det en stark absolut komponent i att utesluta Smith-dominerade kandidater från att vinna. I själva verket innebär det alla de absoluta kriterierna ovan.

Oberoende av irrelevanta alternativ (IIA)

Förändras aldrig resultatet om en icke-vinnande kandidat läggs till eller tas bort (förutsatt att väljarnas preferenser för de andra kandidaterna är oförändrade)? Till exempel misslyckas pluralitetsregeln IIA; lägga till en kandidat X kan göra att vinnaren byter från W till Y trots att Y inte får fler röster än tidigare.

Lokalt oberoende av irrelevanta alternativ (LIIA)

Förändras aldrig resultatet om alternativet som skulle sluta sist tas bort? (Och kan alternativet som slutar tvåa misslyckas med att bli vinnaren om vinnaren togs bort?)

Oberoende av klonalternativ (klonsäkra)

Förändras aldrig resultatet om icke-vinnande kandidater som liknar en befintlig kandidat läggs till? Det finns tre olika fenomen som kan få en metod att misslyckas med detta kriterium:

Spoilerkandidater

som minskar chansen att någon av de liknande eller klonkandidaterna vinner, även känd som en spoilereffekt .

Lag

Uppsättningar av liknande kandidater vars blotta närvaro hjälper chanserna att någon av dem vinner.

Folkmassa

Ytterligare kandidater som påverkar utgången av ett val utan att vare sig hjälpa eller skada deras fraktionsgrupps chanser, utan istället påverka en annan grupp.

Monotonicitetskriterium (monotone)

Om kandidat W vinner för en uppsättning valsedlar, kommer W fortfarande alltid att vinna om dessa valsedlar ändras till rangordning W högre? (Detta innebär också att du inte kan få en förlorande kandidat att vinna genom att ranka dem lägre.)

Konsekvenskriterium (CC)

Om kandidat W vinner för en uppsättning valsedlar, kommer W fortfarande alltid att vinna om dessa valsedlar ändras genom att lägga till ytterligare en uppsättning valsedlar där W vinner också?

Deltagandekriterium (PC)

Är det alltid bättre att rösta ärligt än att inte rösta alls? (Detta är grupperat med det distinkta men liknande konsistenskriteriet i tabellen nedan.)

Omkastningssymmetri (omvändning)

Om individuella preferenser för varje väljare inverteras, vinner den ursprungliga vinnaren aldrig?

Kriterier för rösträkning

Dessa är kriterier som hänför sig till processen att räkna röster och fastställa en vinnare.

Polynomtid (polytime)

Kan vinnaren beräknas i en körtid som är polynom i antal kandidater och linjär i antal väljare?

Lösbar

Kan vinnaren beräknas i nästan alla fall, utan att använda några slumpmässiga processer som att vända mynt? Det vill säga, är exakta band, där vinnaren kan vara en av två eller flera kandidater, försvinnande sällsynta i stora val?

Summerbarhet (som kan summeras)

Kan vinnaren räknas ut genom att räkna ihop valsedlarna vid varje vallokal separat och helt enkelt lägga ihop de individuella rösterna? Mängden information som krävs för sådana sammanräkningar uttrycks som en ordningsfunktion av antalet kandidater N. Långsammare växande funktioner som O(N) eller O(N ² ) gör det lättare att räkna, medan snabbväxande funktioner som O (N!) kan göra det svårare att fånga upp bedrägerier av valadministratörer.

Strategikriterier

Det är kriterier som relaterar till en väljares incitament att använda vissa former av strategi. De skulle också kunna betraktas som relativa resultatkriterier; Men till skillnad från kriterierna i det avsnittet är dessa kriterier direkt relevanta för väljarna; det faktum att en metod klarar dessa kriterier kan förenkla processen att räkna ut sin optimala strategiska röst.

Senare-ingen-skada-kriterium och senare-ingen-hjälp-kriterium

Kan väljarna vara säkra på att om man lägger till en senare preferens till en omröstning inte kommer att skada eller hjälpa någon kandidat som redan är listad?

Inget favoritsvek (NFB)

Kan väljarna vara säkra på att de inte behöver ranka någon annan kandidat över sin favorit för att få ett resultat de föredrar?

Omröstningsformat

Det är frågor som rör uttrycksförmågan eller informationsinnehållet i en giltig röstsedel.

Typ av röstsedel

Vilken information får väljaren på röstsedeln?

Lika grader

Kan en giltig valsedel uttrycka lika stöd för mer än en kandidat (och inte bara lika motstånd till mer än en)?

Över 2 led

Kan en valsedel uttrycka mer än två nivåer av stöd/motstånd för olika kandidater?

Svaghet

Anmärkning om terminologi: Ett kriterium sägs vara "svagare" än ett annat när det godkänns med fler röstningsmetoder. Ofta innebär detta att förutsättningarna för att kriteriet ska gälla är starkare. Till exempel är majoritetskriteriet (MC) svagare än multipelmajoritetskriteriet (MMC), eftersom det kräver att en enda kandidat, snarare än en grupp av vilken storlek som helst, ska vinna. Det vill säga, vilken metod som helst som passerar MMC:n passerar också MC, men inte vice versa; medan alla obligatoriska vinnare under MC måste vinna under MMC, men inte vice versa.

Överensstämmelse med utvalda metoder för en vinnare

Följande tabell visar vilka av ovanstående kriterier som uppfylls av flera ensamvinnaresmetoder.

Sortera:
Kriterium Metod	Majoritet	Maj:t förlorare	Ömsesidig maj.	Condorcet	Cond. förlorare	Smith / ISDA	LIIA	IIA	Klonfast	Monoton	Konsistens	Deltagande	Vändningssymmetri _	Polytid / <a i=2>lösbar resolv­able		Summerbar	Senare-nej-		Inget favoritsvek _	Valsedeltyp _	Rangordnar
																	Skada	Hjälp			=	>2
Godkännande	Betygsatt	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Ja	PÅ)	Ja	PÅ)	Nej	Ja	Ja	Godkännanden	Ja	Nej
Borda räkna	Nej	Ja	Nej	Nej	Ja	Nej	Nej	Nej	Lag	Ja	Ja	Ja	Ja	PÅ)	Ja	PÅ)	Nej	Ja	Nej	Ranking	Ja	Ja
Bucklin	Ja	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Nej	Nej	Nej	PÅ)	Ja	PÅ)	Nej	Ja	Om lika preferenser	Ranking	Ja	Ja
Copeland	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Lag, folksamlingar	Ja	Nej	Nej	Ja	O(N 2 )	Nej	O(N 2 )	Nej	Nej	Nej	Ranking	Ja	Ja
IRV (AV)	Ja	Ja	Ja	Nej	Ja	Nej	Nej	Nej	Ja	Nej	Nej	Nej	Nej	O(N 2 )	Ja	PÅ!)	Ja	Ja	Nej	Ranking	Nej	Ja
Kemeny – Ung	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Spoilers	Ja	Nej	Nej	Ja	PÅ!)	Ja	O(N 2 )	Nej	Nej	Nej	Ranking	Ja	Ja
Majoritetsbedömning Högsta median /	Betygsatt	Ja	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja	Nej	Nej	Beror på	PÅ)	Ja	PÅ)	Nej	Ja	Ja	Poäng	Ja	Ja
Minimax	Ja	Nej	Nej	Ja	Nej	Nej	Nej	Nej	Spoilers	Ja	Nej	Nej	Nej	O(N 2 )	Ja	O(N 2 )	Nej	Nej	Nej	Ranking	Ja	Ja
Pluralitet / <a i=2>FPTP FPTP	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Spoilers	Ja	Ja	Ja	Nej	PÅ)	Ja	PÅ)	N/A	—	Nej	Enkelt märke	—	Nej
Poängomröstning	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Ja	PÅ)	Ja	PÅ)	Nej	Ja	Ja	Poäng	Ja	Ja
Rangordnade par	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Ja	Ja	Nej	Nej	Ja	O(N 3 )	Ja	O(N 2 )	Nej	Nej	Nej	Ranking	Ja	Ja
Omröstning	Ja	Ja	Nej	Nej	Ja	Nej	Nej	Nej	Spoilers	Nej	Nej	Nej	Nej	PÅ)	Ja	PÅ)	Ja	Ja	Nej	Enkelt märke	—	Nej
Schulze	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Ja	Ja	Nej	Nej	Ja	O(N 3 )	Ja	O(N 2 )	Nej	Nej	Nej	Ranking	Ja	Ja
STAR röstning	Nej	Ja	Nej	Nej	Ja	Nej	Nej	Nej	Nej	Ja	Nej	Nej	Beror på	PÅ)	Ja	O(N 2 )	Nej	Nej	Nej	Poäng	Ja	Ja
Sortering , godtycklig vinnare	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Nej	Ja	Ja	Ja	Ja	O(1)	Nej	O(1)	Ja	Ja	Ja	Ingen	—	—
Slumpmässig omröstning	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Ja	PÅ)	Nej	PÅ)	Ja	Ja	Ja	Enkelt märke	—	Nej

Denna tabell är inte heltäckande. Till exempel ingår inte Coombs metod .

Ytterligare jämförelser av röstkriterier finns i artikeln om Schulze-metoden (aka beat path). Vissa data kan dupliceras eftersom dessa tabeller pågår.

Jämförelse av preferensvalsystem

Systemet	Monotona	Condorcet vinnare	Majoritet	Condorcet förlorare	Majoritetsförlorare	Ömsesidig majoritet	Smed	ISDA	LIIA	Oberoende av kloner	Vändningssymmetri	Delaktighet , konsekvens	Laternoharm	Laternohjälp	Polynomtid	Lösbarhet
Schulze	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Ja	Ja	Nej	Nej	Nej	Ja	Ja
Rangordnade par	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Ja	Ja
Tidemans alternativ	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Ja	Nej	Nej	Nej	Nej	Ja	Ja
Kemeny–Young	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Ja	Nej	Nej	Nej	Nej	Ja
Copeland	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Ja	Nej	Nej	Nej	Ja	Nej
Nanson	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Ja	Nej	Nej	Nej	Ja	Ja
Svart	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Ja	Nej	Nej	Nej	Ja	Ja
Omröstning omedelbart	Nej	Nej	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Ja	Nej	Nej	Ja	Ja	Ja	Ja
Smith/IRV	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Ja	Nej	Nej	Nej	Nej	Ja	Ja
Borda	Ja	Nej	Nej	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Nej	Ja	Ja	Ja
Baldwin	Nej	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja
Bucklin	Ja	Nej	Ja	Nej	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja
Mångfald	Ja	Nej	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja	Ja
Kontingent omröstning	Nej	Nej	Ja	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja
Coombs	Nej	Nej	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja
MiniMax [	Ja	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja
Anti-pluralitet	Ja	Nej	Nej	Nej	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Nej	Nej	Ja	Ja
Sri Lankas kontingentomröstning	Nej	Nej	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja
Kompletterande omröstning	Nej	Nej	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja	Ja	Ja	Ja
Dodgson	Nej	Ja	Ja	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Nej	Ja

Jämförelse av system med flera vinnare

Valsystem med flera vinnare strävar som bäst efter att producera församlingsrepresentanter i en vidare mening än att fatta samma beslut som skulle fattas av enstaka vinnarröster. De kan också vara vägen till enpartissvep av en stads säten, om ett icke-proportionellt system, såsom Plurality block röstning eller biljettröstning , används.

Nya Zeelands kungliga kommission för valsystemet listade tio kriterier för deras utvärdering av möjliga nya valmetoder för Nya Zeeland . Dessa inkluderade rättvisa mellan politiska partier, effektiv representation av minoriteter eller särskilda intressegrupper, politisk integration, effektivt väljardeltagande och legitimitet.

Mätvärden för utvärderingar av flera vinnare

Att utvärdera resultatet av röstningsmetoder med flera vinnare kräver andra mätvärden än vad som används för system med ensam vinnare. Följande har föreslagits.

• Condorcet Committee Efficiency (CCE) mäter sannolikheten att en grupp valda vinnare skulle slå alla förlorare i parvisa lopp.
• Social-Utility Proportionality (SUP) mäter sannolikheten att varje väljare har minst en högnyttig kandidat bland vinnarna.
• Egalitarian-Utility Proportionality (EUP) mäter proportionalitet i termer av väljaren med lägst nytta för den närmast vinnande kandidaten.
• Centrist Tendency (CT) mäter sannolikheten för en metod för att välja kandidater nära mitten eller ytterligheterna av ett politiskt spektrum.
• Gallagher Index och Loosemore–Hanby index (LH) mäter proportionaliteten mellan mandatandel och partiröstandel. Gallagher använder generellt övergripande röstpartiprocenter eller röster jämfört med mandatprocenter för att bedöma proportionalitet så ignorerar närvaron av distrikt om några.
• Orepresenterad röst mäter andelen väljare som inte representeras av någon förtroendevald, röster som inte användes för att välja någon.

Kriterietabeller

Överensstämmelse med partibaserade metoder för flera vinnare

Kriterium Metod	Proportionell i teorin, förutsatt att det inte finns någon valtröskel	Proportionell i praktiken , förutsatt att det inte finns någon valtröskel	Halvproportionell en majoritet av väljarna kan inte tvinga resultatet att bli ett sådant att de vinner alla mandat	Inte brytbar röstningsmetod har inte en potentiell strategisk röståterkopplingsslinga	Monoton	Konsistens	Deltagande	Universellt omtyckta kandidater	Finns det nivåer av medlemmar?	Krävs lokal representation?	Finns det väljarval av enskilda kandidater?	Typ av valsedel
Allmän biljett	Nej	Nej	Nej	Nej – Tvåpartsdominans	Ja	Ja	Ja	Nej	Nej	Nej	Nej – alla platser fylls från en förutbestämd lista	Enkelt märke för en lista
Stängd partilista	Ja	Ja	Ja	Ja (såvida inte få platser eller hög tröskel för första plats)	Ja	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Nej	Nej	Nej – rangordningen av kandidater inom partiets lista avgör i vilken ordning partiets platser fylls	Enkelt märke för en lista
Relativt sluten partilista	Ja	Ja	Ja	Ja (såvida inte få platser eller hög tröskel för första plats)	Ja	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Nej	Nej	Ja – en kandidat behöver skaffa en Hare-kvot för att vara garanterad en plats, annars avgör rangordningen av kandidater inom partiets lista i vilken ordning partiets platser fylls	Enstaka eller begränsade poäng för kandidater inom en lista
Öppenare partilista	Ja	Ja	Ja	Ja (såvida inte få platser eller hög tröskel för första plats)	Ja	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Nej	Nej	Ja – en kandidat behöver få en andel av rösterna för att vara garanterad en plats, annars avgör rangordningen av kandidater inom partiets lista i vilken ordning partiets platser fylls	Enstaka eller begränsade poäng för kandidater inom en lista
Mest öppna parti-listan	Ja	Ja	Ja	Ja (såvida inte få platser eller hög tröskel för första plats)	Ja	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Nej	Nej	Ja – antalet röster varje kandidat får avgör i vilken ordning partiets platser fylls	Enkelt betyg för en kandidat inom en lista
Parti-lista med panachage	Ja	Ja	Ja	Ja (såvida inte få platser eller hög tröskel för första plats)	Ja	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Nej	Nej	Ja – antalet röster varje kandidat får avgör i vilken ordning partiets platser fylls	Begränsade poäng för kandidater inom alla listor
Blandad medlem proportionell , listuppladdning, två röster	Nej – strategiska väljare kan manipulera antalet överhängsplatser	Ja, exklusive disproportionaliteter orsakade av överhängsplatser – ledamöter i proportionell nivå väljs ut för att kompensera för eventuella oproportioner som orsakas av valkretsnivån, endast baserat på de proportionella rösterna	Ja	Nej – Överhängsmanipulation och tvåpartidominans bland enstaka vinnarplatser	Ja	Nej	Ja	Delvis – en allmänt omtyckt lista skulle behöva vinna alla mandat i både proportionell och valkretsnivå per definition; om alla valkretskandidater är allmänt omtyckta, skulle urvalet av proportionella ledamöter göras för att kompensera för den efterföljande oproportionaliteten i det totala medlemskapet	Ja – valkretsnivå och proportionell nivå	Ja – enmansvalkretsar	Ja – valkretskandidater väljs ut med en enda vinnarmetod; urval av proportionella skiktmedlemmar kan göras med någon av de partilista metoder som nämns ovan	Enkelt betyg eller rangordning för en valkretskandidat; proportionella nivåmärken beror på den exakta metoden som används för valet
Bästa förlorare Blandad medlem proportionell	Nej – strategiska väljare kan manipulera antalet överhängsplatser	Ja, exklusive disproportionaliteter orsakade av överhängsplatser – proportionella ledamöter väljs ut för att kompensera för eventuella disproportionaliteter som orsakas av valkretsnivån, baserat på partiets totalsummor	Ja	Nej – Överhängsmanipulation och tvåpartidominans bland enstaka vinnarplatser	Ja	Nej	Ja	Nej – en allmänt omtyckt lista skulle behöva vinna alla platser i både proportionella och valkretsnivåer per definition – eftersom de proportionella ledamöterna dras från valkretsförlorarna är en sådan bedrift omöjlig; om alla valkretskandidater är allmänt omtyckta, skulle urvalet av proportionella ledamöter göras för att kompensera för den efterföljande oproportionaliteten i det totala medlemskapet	Ja – valkretsnivå och proportionell nivå	Ja – enmansvalkretsar	Ja – valkretskandidater väljs ut med en enda vinnarmetod; proportionella nivåmedlemmar väljs genom en partilista-metod	Enkelt betyg eller rangordning för en valkretskandidat; proportionell nivå som bestäms av valkretsnivåns resultat
Parallellomröstning	Nej	Nej – medlemmar i valkretsnivå och proportionell nivå väljs oberoende av varandra	Ja	Nej – Tvåpartidominans bland enstaka vinnarplatser	Ja	Nej	Ja	Delvis – en allmänt gillad lista skulle behöva vinna alla platser i den proportionella nivån per definition; om alla valkretskandidater är allmänt omtyckta, skulle urvalet av proportionella ledamöter inte påverkas	Ja – valkretsnivå och proportionell nivå	Ja – enmansvalkretsar	Ja – valkretskandidater väljs ut med en enda vinnarmetod; proportionella nivåmedlemmar väljs genom en partilista-metod	Enkelt betyg eller rangordning för en valkretskandidat; proportionella nivåmärken beror på den exakta metoden som används för valet
Scorpo	Nej – strategiska väljare kan dela upp biljetten för att ta bort kompensationssubtraktionen och på så sätt återställa valet till parallellröstning	Delvis – ledamöter i valkretsnivå och proportionella nivåer väljs oberoende av varandra, men valkretsvinnarnas röster dras av från deras respektive partilistor.	Ja	Nej – locklistor	Nej	Nej	Nej	Ja – en allmänt gillad lista har fortfarande rösterna från sina valkretsvinnare subtraherade från sin egen summa, vilket säkerställer en proportionell fördelning mellan alla andra platser; om alla valkretskandidater är allmänt omtyckta, skulle urvalet av proportionella ledamöter göras med deras röster subtraherade från deras partiers totalsumma	Ja – valkretsnivå och proportionell nivå	Ja – enmansvalkretsar	Ja – valkretskandidater väljs ut med en enda vinnarmetod; proportionella nivåmedlemmar väljs genom en partilista-metod	Enkelt betyg eller rangordning för en valkretskandidat; proportionella nivåmärken beror på den exakta metoden som används för valet
Majoritetsbonussystem	Delvis – en majoritet av platserna fördelas proportionellt mellan partierna, men resten ges som bonus till det mest röstade partiet; Strategiska väljare kan manipulera denna bonus	Delvis – en majoritet av platserna fördelas proportionellt mellan partierna, men resten ges som bonus till det mest röstade partiet	Ja	Nej – Tvåpartsdominans bland parter som konkurrerar om bonus	Ja	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Ja – proportionell nivå och bonusnivå	Nej	Inte nödvändigtvis – urval av proportionella nivåmedlemmar kan göras med någon av partilistmetoderna som nämns ovan	Proportionella nivåmärken beror på den exakta metoden som används för urval; bonusnivå som bestäms av de proportionella nivåerna
Majoritetsjackpottsystem	Nej – jackpotten tilldelas det partiet som röstas mest för, och platserna utanför jackpottnivån fördelas proportionellt mellan alla andra; Strategiska väljare kan manipulera jackpotten	Nej – jackpotten tilldelas det partiet som röstas mest för, och platserna utanför jackpottnivån fördelas proportionellt mellan alla andra	Ja	Nej – Tvåpartsdominans bland parter som konkurrerar om jackpotten	Nej – den som vinner jackpotten får en fördel framför alla andra; jackpotten förvandlas till en nackdel för det mest röstade partiet om det fick en större andel av platserna än jackpotten	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Ja – proportionell nivå och jackpottnivå	Nej	Inte nödvändigtvis – urval av proportionella nivåmedlemmar kan göras med någon av partilistmetoderna som nämns ovan	Proportionella nivåmärken beror på den exakta metoden som används för urval; jackpottnivå bestäms av de proportionella nivåresultaten
Dubbelledad proportionell	Nej – strategiska väljare kan teoretiskt manipulera resultaten i sekundära mandat	Ja	Ja	Nej – Sekundär mandatmanipulation och tvåpartidominans bland primära platser	Nej	Ja	Ja	Ja	Nej	Ja – valkretsar med två medlemmar	Ja – kandidaten med flest röster är garanterad en plats, och den andra väljs bland de bästa förlorarna	Enkelt betyg för en kandidat eller ett par kandidater
Landsbygds-stads proportionell representation	Nej – strategiska väljare kan manipulera antalet överhängsplatser på landsbygden	Delvis – disproportionaliteter kan orsakas av användningen av STV i stadssäten, såväl som överhängande landsbygdssäten – landsbygdens proportionella nivåmedlemmar väljs ut för att kompensera för eventuella oproportionerligheter som orsakas av landsbygdens valkretsnivå, men ingen sådan kompensation finns för urbana oproportionerligheter	Ja	Nej – överhängsmanipulation och tvåpartidominans bland enstaka vinnarplatser på landsbygden	Nej	Nej	Nej	Delvis – ja i den urbana nivån; en allmänt omtyckt landsbygdslista skulle per definition behöva vinna alla platser i landsbygdens proportionella nivå; om alla landsbygdskandidater är allmänt omtyckta, skulle urvalet av landsbygdsproportionella ledamöter göras för att kompensera för oproportionaliteten; i båda fallen skulle urvalet av urbana kandidater inte påverkas	Ja – stadsnivå, landsbygdens valkretsnivå och landsbygdens proportionella nivå	Ja – stadsvalkretsar och enmansdistrikt på landsbygden	Ja – landsbygdskandidater väljs ut av STV ; Landsbygdskandidater väljs ut med en enda vinnaremetod; ledamöter på landsbygdens proportionella nivå kan väljas genom en partilistmetod eller bland de bästa förlorarna i landsbygdens valkretsar	Ranking för kandidater i stadsvalkretsar; enda poäng eller rangordning för en kandidat för en landsbygdsvalkrets; lantliga proportionella nivåmärken beror på den exakta metoden som används för urval
Extra röst	Ja	Ja	Ja	Ja – beroende på genomförandet av partirankningen	Ja – beroende på genomförandet av partirankningen	Ja	Ja	N/A – en allmänt gillad lista skulle behöva vinna alla platser per definition	Nej	Nej – Proportionell variant med blandade medlemmar möjlig	Nej – Proportionell variant med blandade medlemmar möjlig	Enskilt märke eller ranking för partier

Överensstämmelse med icke-majoritära partiagnostiska metoder för flera vinnare

Följande tabell visar vilka av ovanstående kriterier som uppfylls av flera vinnarmetoder.

Kriterium Metod	Proportionell	Monoton	Konsistens	Warrens deltagandekriterium för flera vinnare	Inget favoritförräderi _	Halvärlig	Universellt omtyckta kandidater	Med ensam vinnare	Typ av valsedel
Monroe's (poängomröstningsversion)	Ja	Beror på vilken tiebreaker som används		Ja	Nej	Nej		Godkännande eller Range	Godkännanden eller poäng
Chamberlin-Courant regel
Eberts	Ja	Nej					Ja	Godkännande eller Range	Godkännanden eller poäng
Psi	Ja	Ja		Ja	Nej	Nej	Nej	Godkännande eller Range	Godkännanden eller poäng
Harmonisk	Ja	Ja		Ja	Nej	Nej	Nej	Godkännande eller Range	Godkännanden eller poäng
Sekventiellt proportionellt godkännande	Ja	Ja		Nej	Nej	Nej	Nej	Godkännande	Godkännanden
Omvägt intervall	Ja	Ja		Nej	Nej	Nej	Nej	Räckvidd	Poäng
Proportionellt godkännande	Ja	Ja		Ja	Nej	Nej	Nej	Godkännande	Godkännanden
Budröstning	Ja				Nej	Nej	Ja	Godkännande eller Range	Godkännanden eller poäng
En överlåtbar röst	Ja	Nej	Nej	Nej	Nej	Nej	Ja	Omedelbar avrinning	Ranking
CPO-STV	Ja	Nej	Nej	Nej	Nej	Nej	Ja	En Condorcet-metod (beror på vilken)	Ranking
Schulze STV	Ja	Ja	Nej	Nej	Nej	Nej	Ja	Schulze	Ranking
Phragmen									Godkännanden eller rankningar
Kvot Borda System									Ranking
STV med Borda Elimination									Ranking
[STV med Bottom Two Runoff]									Ranking
QPQ									Ranking
Regel för expanderande godkännanden									Ranking
Sekventiell STV									Ranking
En enda röst som inte kan överföras	Nej	Ja	Ja	Ja	Nej	Nej	— (ej proportionell)	Mångfald	Enkelt märke
Begränsad röst	Nej	Ja	Ja	Ja	Nej	Nej	— (ej proportionell)	Mångfald	Begränsade märken
Kumulativ röstning	Nej	Ja	Ja	Ja	Nej	Nej	— (ej proportionell)	Mångfald	Flera märken
Minmax godkännande								Godkännande	Godkännanden
Sortering , godtycklig vinnare	Nej	Ja	Ja	Ja	Ja	Ja	— (ej proportionell)	Sortering , godtycklig vinnare	Ingen
Enkel slumpmässig omröstning	Nej	Ja	Ja	Ja	Ja	Ja	— (ej proportionell)	Slumpmässig omröstning	Begränsade märken
Flera slumpmässiga omröstningar	Närmar sig	Ja	Ja	Ja	Ja	Ja	— (ej proportionell)	Slumpmässig omröstning	Begränsad ranking

Överensstämmelse med majoritära partiagnostiska metoder för flera vinnare

Följande tabell visar vilka av ovanstående kriterier som uppfylls av flera vinnarmetoder.

Kriterium Metod	Monoton	Konsistens	Deltagande	Klonfast	Inget favoritsvek	Halvärlig	Smith satte vinnare	Condorcet vinnare	Condorcet förlorare	Med singelvinnare	Valsedeltyp _
Flera vinnare godkännande	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Godkännande	Godkännanden
Flera vinnare	Ja	Ja	Ja	Ja	Ja	Ja	Nej	Nej	Nej	Räckvidd	Poäng
Flerfaldig vinnare Schulze	Ja	Nej	Nej	Ja	Nej	Nej	Ja	Ja	Ja	Schulze	Ranking
I stora drag	Ja	Ja	Ja	Nej (spoilers)	Nej	Nej	Nej	Nej	Nej	Mångfald	Begränsade märken

Se även

• Rangordnad röstning
• Arrows omöjlighetsteorem
• Kardinalnytta och ordinalnytta
• Condorcet paradox