Hilbert system

Inom matematisk fysik är . Hilbert-systemet en sällan använd term för ett fysiskt system som beskrivs av en C* -algebra

Inom logik , särskilt matematisk logik , är ett Hilbert-system , ibland kallat Hilbert-kalkyl , Hilbert-stil deduktivt system eller Hilbert-Ackermann-system , en typ av system av formell deduktion som tillskrivs Gottlob Frege och David Hilbert . Dessa deduktiva system studeras oftast för första ordningens logik , men är också av intresse för andra logiker.

De flesta varianter av Hilbert-system har ett karakteristiskt grepp i hur de balanserar en avvägning mellan logiska axiom och inferensregler . Hilbertsystem kan kännetecknas av valet av ett stort antal scheman av logiska axiom och en liten uppsättning inferensregler . System med naturligt deduktion tar motsatt väg, inklusive många avdragsregler men väldigt få eller inga axiomscheman. De vanligast studerade Hilbert-systemen har antingen bara en slutledningsregel – modus ponens , för propositionslogik – eller två – med generalisering , för att hantera predikatlogik också – och flera oändliga axiomscheman. Hilbert-system för propositionell modal logik , ibland kallad Hilbert-Lewis-system, axiomatiseras i allmänhet med två ytterligare regler, nödvändighetsregeln och den enhetliga substitutionsregeln.

Ett karakteristiskt drag för de många varianterna av Hilbert-system är att kontexten inte ändras i någon av deras inferensregler, medan både naturlig deduktion och sekventiell kalkyl innehåller några kontextförändrande regler. Således, om man bara är intresserad av tautologiers härledningsförmåga, inga hypotetiska bedömningar, så kan man formalisera Hilbert-systemet på ett sådant sätt att dess slutledningsregler endast innehåller bedömningar av en ganska enkel form. Samma sak kan inte göras med de andra två deduktionssystemen: eftersom kontexten ändras i vissa av deras inferensregler kan de inte formaliseras så att hypotetiska bedömningar skulle kunna undvikas – inte ens om vi vill använda dem bara för att bevisar härledning av tautologier.

Formella avdrag

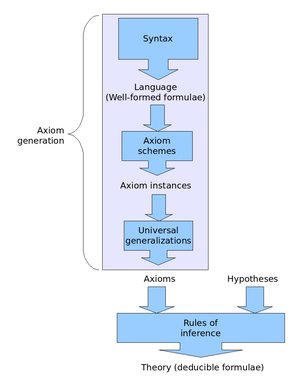
I ett deduktionssystem i Hilbert-stil är en formell deduktion en ändlig sekvens av formler där varje formel antingen är ett axiom eller erhålls från tidigare formler genom en slutledningsregel. Dessa formella avdrag är avsedda att spegla bevis på naturliga språk, även om de är mycket mer detaljerade.

Antag att $\Gamma$ är en uppsättning formler som betraktas som hypoteser . Till exempel $\Gamma$ vara en uppsättning axiom för gruppteori eller mängdteori . Notationen $\Gamma \vdash \phi$ betyder att det finns en deduktion som slutar med att $\phi$ använder som axiom endast logiska axiom och element av $\Gamma$ . Så informellt $\Gamma \vdash \phi$ att $\phi$ är bevisbart om man antar alla formler i $\Gamma$ .

Hilbert-stil deduktionssystem kännetecknas av användningen av många scheman av logiska axiom . Ett axiomschema är en oändlig uppsättning axiom som erhålls genom att ersätta alla formler av någon form i ett specifikt mönster. Uppsättningen av logiska axiom inkluderar inte bara de axiom som genereras från detta mönster, utan också all generalisering av ett av dessa axiom. En generalisering av en formel erhålls genom att prefixera noll eller fler universella kvantifierare på formeln; till exempel $\forall y(\forall xPxy\to Pty)$ är en generalisering av $\forall xPxy\ till Pty$ .

Logiska axiom

Det finns flera variantaxiomatiseringar av predikatslogik, eftersom det för vilken logik som helst finns frihet att välja axiom och regler som kännetecknar den logiken. Vi beskriver här ett Hilbert-system med nio axiom och bara regeln modus ponens, som vi kallar enregelaxiomatiseringen och som beskriver klassisk ekvationell logik. Vi sysslar med ett minimalt språk för denna logik, där formler endast använder kopplingarna $\lnot$ och $\to$ och endast kvantifieraren $\forall$ . Senare visar vi hur systemet kan utökas till att inkludera ytterligare logiska kopplingar, såsom $\land$ och $\lor$ , utan att förstora klassen av deducerbara formler.

De första fyra logiska axiomscheman tillåter (tillsammans med modus ponens) manipulation av logiska bindningar.

P1. $\phi \to \phi$

P2. $\phi \to \left(\psi \to \phi \right)$

P3. ${\displaystyle \left(\phi \to \left(\psi \rightarrow \xi \right)\right)\to \left(\left(\phi \to \psi \right)\to \left(\phi \to \xi \right)\right)} P4$

. $\left(\lnot \phi \to \lnot \psi \right)\to \left(\psi \to \phi \right)$

Axiomet P1 är redundant, som det följer av P3, P2 och modus ponens (se bevis ). Dessa axiom beskriver klassisk propositionell logik ; utan axiom P4 får vi positiv implikationslogik . Minimal logik uppnås antingen genom att istället lägga till axiomet P4m, eller genom att definiera $\lnot \phi$ som $\phi \to \bot$ .

P4m. $\left(\phi \to \psi \right)\to \left(\left(\phi \to \lnot \psi \right )\to \lnot \phi \right)$

Intuitionistisk logik uppnås genom att lägga till axiom P4i och P5i till positiv implikationslogik, eller genom att lägga till axiom P5i till minimal logik. Både P4i och P5i är teorem för klassisk propositionslogik.

P4i. $\left(\phi \to \lnot \phi \right)\to \lnot \phi$

P5i. $\lnot \phi \to \left(\phi \to \psi \right)$

Observera att dessa är axiomscheman, som representerar oändligt många specifika instanser av axiom. Till exempel kan P1 representera den specifika axiominstansen $p\to p$ , eller så kan den representera $\left(p\to q\right) \to \left(p\to q\right)$ : $\phi$ är en plats där vilken formel som helst kan placeras. En variabel som denna som sträcker sig över formler kallas en "schematisk variabel".

Med en andra regel för enhetlig substitution (US) kan vi ändra vart och ett av dessa axiomscheman till ett enda axiom, och ersätta varje schematisk variabel med någon propositionsvariabel som inte nämns i något axiom för att få vad vi kallar substitutionsaxiomatisering. Båda formaliseringarna har variabler, men där enregelaxiomatiseringen har schematiska variabler som ligger utanför logikens språk, använder substitutionsaxiomatiseringen propositionella variabler som gör samma arbete genom att uttrycka idén om en variabel som sträcker sig över formler med en regel som använder substitution.

USA. Låt $\phi (p)$ vara en formel med en eller flera instanser av propositionsvariabeln $p$ , och låt $\psi$ vara en annan formel. Sedan från $\phi (p)$ , sluta $\phi (\psi )$ .

De följande tre logiska axiomscheman ger sätt att lägga till, manipulera och ta bort universella kvantifierare.

F5. $\forall x\left(\phi \right)\to \phi [x:=t]$ där t kan ersätta x i $\,\!\phi$

F6. $\forall x\left(\phi \to \psi \right)\to \left(\forall x\left( \phi \right)\to \forall x\left(\psi \right)\right)$

F7. $\phi \to \forall x\left(\phi \right)$ där x inte är ledig i $\phi$ .

Dessa tre ytterligare regler utvidgar propositionssystemet till att axiomatisera klassisk predikatlogik . På samma sätt utvidgar dessa tre regler systemet för intuitionistisk propositionslogik (med P1-3 och P4i och P5i) till intuitionistisk predikatlogik.

Universell kvantifiering ges ofta en alternativ axiomatisering med hjälp av en extra generaliseringsregel (se avsnittet om Metateorem), i vilket fall reglerna Q6 och Q7 är redundanta.

De slutliga axiomscheman krävs för att arbeta med formler som involverar likhetssymbolen.

I8. $x=x$ för varje variabel x .

I9. $\left(x=y\right)\to \left(\phi [z:=x]\to \phi [z:=y]\right)$

Konservativa tillägg

Det är vanligt att i ett deduktionssystem i Hilbert-stil endast inkludera axiom för implikation och negation. Med tanke på dessa axiom är det möjligt att bilda konservativa förlängningar av deduktionsteoremet som tillåter användning av ytterligare bindemedel. Dessa tillägg kallas konservativa eftersom om en formel φ som involverar nya kopplingar skrivs om till en logiskt ekvivalent formel θ som endast involverar negation, implikation och universell kvantifiering, så är φ härledbar i det utökade systemet om och endast om θ är härledbart i det ursprungliga systemet . När det är helt utbyggt kommer ett Hilbert-liknande system att likna mer ett system med naturlig deduktion .

Existentiell kvantifiering

• Inledning

$\forall x(\phi \to \exists y(\phi [x:=y]))$

• Elimination

$\forall x(\phi \to \psi )\to \exists x(\phi )\to \psi$ där $x$ inte är en fri variabel av $\psi$ .

Konjunktion och disjunktion

• Konjunktionsintroduktion och elimineringsintroduktion

: $\alpha \to (\beta \to \alpha \land \beta )$

eliminering vänster: $\alpha \wedge \beta \to \alpha$

eliminering höger: $\alpha \wedge \beta \to \beta$

• Disjunktion introduktion och eliminering

introduktion vänster: $\alpha \to \alpha \vee \beta$

inledning höger: $\beta \to \alpha \vee \beta$

eliminering: ${\ visningsstil (\alpha \to \gamma )\to ((\beta \to \gamma )\to \alpha \vee \beta \to \gamma )}$

Metateorem

Eftersom Hilbert-liknande system har väldigt få avdragsregler är det vanligt att bevisa metateorem som visar att ytterligare avdragsregler inte ger någon deduktiv kraft, i den meningen att ett avdrag med de nya avdragsreglerna kan omvandlas till ett avdrag med endast det ursprungliga avdraget regler.

Några vanliga metateorem av denna form är:

• Deduktionssatsen : $\Gamma ;\phi \vdash \psi$ _ om och endast om $\Gamma \vdash \phi \to \psi$ .
• $\Gamma \vdash \phi \leftrightarrow \psi$ om och endast om $\Gamma \vdash \phi \to \psi$ och ${\ displaystyle \Gamma \vdash \psi \to \phi }$ .
• Kontraposition: Om $\Gamma ;\phi \vdash \psi$ sedan $\Gamma ;\lnot \psi \vdash \lnot \phi$ .
• Generalisering : Om $\Gamma \vdash \phi$ och x inte förekommer fritt i någon formel för $\Gamma$ då $\Gamma \vdash \forall x\ phi$ .

Några användbara satser och deras bevis

Följande är flera satser inom propositionell logik, tillsammans med deras bevis (eller länkar till dessa bevis i andra artiklar). Observera att eftersom (P1) i sig kan bevisas med de andra axiomen, räcker det faktiskt med (P2), (P3) och (P4) för att bevisa alla dessa satser.

(HS1) $(q\to r)\to ((p\to q)\to (p\to r))$ - Hypotetisk syllogism , se bevis .

(L1) $p\to ((p\to q)\to q)$ - bevis:

(1) $((p\to q)\to (p\to q))\to (((p\to) q)\to p)\to ((p\to q)\to q))$ (instans av (P3))

(2) $(p\to q) )\to (p\to q)$ (instans av (P1))

(3) $((p\to q)\ till p)\to ((p\to q)\to q)$ (från (2) och (1) av modus ponens )

(4) $(((p\to q)\to p)\ till ((p\till q)\till q))\till ((p\till ((p\till q)\till p))\till (p\till ((p\till q)\till q)) )$ (instans av (HS1))

(5) $(p\to ((p\ till q)\to p))\to (p\to ((p\to q)\to q))$ (från (3) och (4) av modus ponens)

(6) $p\to ((p\to q)\to p)$ (instans av (P2))

(7) $p\to ( (p\to q)\to q)$ (från (6) och (5) av modus ponens)

Följande två satser är kända tillsammans som dubbelnegation :

(DN1) $\neg \neg p\to p$

(DN2) $p\to \neg \neg p$

Se bevis .

(L2) $(p\to (q\to r))\to (q\to (p\to r))$ - för detta bevis använder vi metoden för den hypotetiska syllogism metateorem som en stenografi för flera bevissteg:

(1) ${\displaystyle (p\to (q\to r))\to ((p\to q)\to (p\to r))} ($ instans av (P3))

(2) $((p\to q)\to (p\to r))\to ((q\ till (p\to q))\to (q\to (p\to r)))$ (instans av (HS1))

(3) $(p\to (q\to r))\to ((q\to (p\to q))\to (q\to (p) \to r)))$ (från (1) och (2) med den hypotetiska syllogism metateorem)

(4) $((p\to (q\to r))\to ((q\to (p\to q))\to (q\to (p\to r))))\to (((p\till (q\till r))\till (q\till (p\till q)))\till ((p\till (q\till r))\till (q\till (p\ till r))))$ (instans av (P3))

(5) $((p\to (q\to r))\to (q\to (p\to q)))\to ((p\to (q\to) r))\to (q\to (p\to r)))$ (från (3) och (4) med modus ponens)

(6) $q\to (p\ till q)$ (instans av (P2))

(7) ${\displaystyle (q) \to (p\to q))\to ((p\to (q\to r))\to (q\to (p\to q)))} (instans av (P2)) ($ 8

) ${\displaystyle (p\to (q\to r))\to (q\to (p\to q))} ($ från (6) och (7) använda modus ponens)

(9) $(p\to (q\to r))\to (q\to (p\to r))$ (från (8) och (5) med modus ponens)

(HS2) $(p\to q)\to ((q\to r)\to (p\to r))$ - en alternativ form av den hypotetiska syllogismen . bevis:

(1) $(q\to r)\to ((p\to q)\to (p\to r) )$ (instans av (HS1))

(2) $((q\to r)\to ((p\to q)\to (p\to r)))\to ((p\to q)\to ((q\to r)\to (p\to r)))$ (instans av (L2))

(3) $(p\to q )\to ((q\to r)\to (p\to r))$ (från (1) och (2) av modus ponens)

(TR1) ${ \displaystyle (p\to q)\to (\neg q\to \neg p)}$ - Transponering, se bevis (den andra transponeringsriktningen är (P4)).

(TR2) $(\neg p\to q)\to (\neg q\to p)$ - en annan form av transponering; bevis:

(1) ${\displaystyle (\neg p\to q)\to (\neg q\to \neg \neg p)} ($ instans av ( TR1))

(2) $\neg \neg p\to p$ (instans av (DN1))

(3) ${\displaystyle (\neg \neg p\to p)\to ((\neg q\to \neg \neg p)\to (\neg q\to p))} ($ instans av (HS1))

(4) $(\neg q\to \neg \neg p)\to (\neg q\to p)$ ( från (2) och (3) av modus ponens)

(5) $(\neg p\to q)\to (\neg q\to p)$ (från (1) och (4) med den hypotetiska syllogism-metateorem)

(L3) $(\neg p\to p)\to p$ - bevis:

(1) $\neg p\to (\neg \neg (q\to q)\to \neg p)$ (instans av (P2))

(2) $(\neg \neg (q\to q)\to \neg p)\to (p\to \neg ( q\to q))$ (instans av (P4))

(3) $\neg p\to (p\to \neg (q\to q) )$ (från (1) och (2) med den hypotetiska syllogism-metateorem)

(4) $(\neg p\to (p\to \neg (q\to q)))\to ((\neg p\to p)\to (\neg p\to \neg (q\to q)))$ (instans av (P3))

(5) $(\neg p\to p)\to (\neg p\to \neg (q\till q))$ (från (3) och (4) med lägena ponens)

(6) ${\displaystyle (\neg p\to \neg (q\to q))\to ((q\to q)\to p)} ($ instans av (P4))

(7) $(\neg p\to p)\to ((q\to q)\to p)$ (från (5) och (6) med hjälp av den hypotetiska syllogismmetateorem )

(8) $q\to q$ (instans av (P1))

(9) $(q\ till q)\to (((q\to q)\to p)\to p)$ (instans av (L1))

(10) $((q\ till q)\to p)\to p$ (från (8) och (9) med lägen ponens)

(11) $(\neg p\to p)\to p$ (från (7) och (10) med den hypotetiska syllogism metateorem)

Alternativa axiomatiseringar

Ytterligare information: Lista över logiksystem

Axiom 3 ovan krediteras Łukasiewicz . Det ursprungliga systemet av Frege hade axiom P2 och P3 men fyra andra axiom istället för axiom P4 (se Freges propositionskalkyl ) . Russell och Whitehead föreslog också ett system med fem propositionella axiom.

Ytterligare kopplingar

Axiomen P1, P2 och P3, med deduktionsregeln modus ponens (formaliserande intuitionistisk propositionslogik), motsvarar kombinatoriska logiska baskombinatorer I , K och S med applikationsoperatorn. Bevis i Hilbert-systemet motsvarar då kombinatortermer i kombinatorisk logik. Se även Curry–Howard-korrespondens .

Se även

• Lista över Hilbert-system
• Naturligt avdrag

Anteckningar

• Curry, Haskell B.; Robert Feys (1958). Combinatory Logic Vol. jag . Vol. 1. Amsterdam: Norra Holland.
•   Monk, J. Donald (1976). Matematisk logik . Examentexter i matematik. Berlin, New York: Springer-Verlag . ISBN 978-0-387-90170-1 .
• Ruzsa, Imre; Máté, András (1997). Bevezetés a modern logikába (på ungerska). Budapest: Osiris Kiadó.
• Tarski, Alfred (1990). Bizonyítás és igazság (på ungerska). Budapest: Gondol. Det är en ungersk översättning av Alfred Tarskis utvalda artiklar om semantisk sanningsteori .
• David Hilbert (1927) "The foundations of mathematics", översatt av Stephan Bauer-Menglerberg och Dagfinn Føllesdal (s. 464–479). i:
  •   van Heijenoort, Jean (1967). Från Frege till Gödel: A Source Book in Mathematical Logic, 1879–1931 (3:e tryckningen 1976 uppl.). Cambridge MA: Harvard University Press. ISBN 0-674-32449-8 .
  • Hilberts 1927, baserat på en tidigare 1925 "foundations"-föreläsning (sid. 367–392), presenterar hans 17 axiom -- implikationsaxiom #1-4, axiom om & och V #5-10, negationsaxiom #11- 12, hans logiska ε-axiom #13, jämlikhetsaxiom #14-15 och axiom för nummer #16-17 -- tillsammans med de andra nödvändiga elementen i hans formalistiska "bevisteori" -- t.ex. induktionsaxiom, rekursionsaxiom, etc; han erbjuder också ett livligt försvar mot LEJ Brouwers intuitionism. Se även Hermann Weyls (1927) kommentarer och genmäle (s. 480–484), Paul Bernays (1927) bilaga till Hilberts föreläsning (s. 485–489) och Luitzen Egbertus Jan Brouwers (1927) svar (s. 490–495)
•   Kleene, Stephen Cole (1952). Introduktion till metamatematik (10:e intrycket med 1971 års rättelser utg.). Amsterdam NY: North Holland Publishing Company. ISBN 0-7204-2103-9 .
  • Se särskilt kapitel IV Formella system (sid. 69–85) där Kleene presenterar underkapitel §16 Formella symboler, §17 Formationsregler, §18 Fria och bundna variabler (inklusive substitution), §19 Transformationsregler (t.ex. modus ponens) -- och från dessa presenterar han 21 "postulat" -- 18 axiom och 3 "omedelbar konsekvens"-relationer uppdelade enligt följande: Postulat för propostalkalkylen #1-8, Ytterligare postulat för predikatkalkylen #9-12, och Ytterligare postulat för talteori #13-21.

externa länkar

• Gaifman, Haim. "Ett deduktivt system av Hilbert-typ för sentential logik, fullständighet och kompakthet" ( PDF) .
• Farmer, WM "Propositionell logik" (PDF) . Den beskriver (bland annat) en del av deduktionssystemet i Hilbert-stil (begränsat till propositionskalkyl ).