Tensegritet

För rörelsesystemet skapat av Carlos Castaneda, se Tensegrity (Castaneda) .

Den enklaste tensegrity-strukturen (ett T3-prisma). Var och en av tre kompressionselement (grön) är symmetriska med de andra två och symmetriska från ände till ände. Varje ände är ansluten till tre kablar (röda), som ger spänning och exakt definierar läget för den änden på samma sätt som de tre kablarna i Skylon definierar den nedre änden av dess avsmalnande pelare.

Stereobild

Höger ram Vänster

ram

Cross-eye view ( )

Parallell vy ( ) Animation

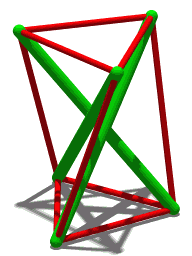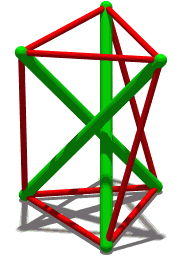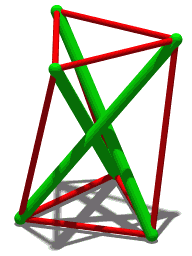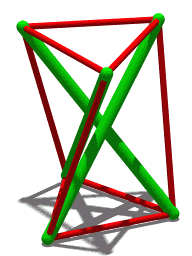
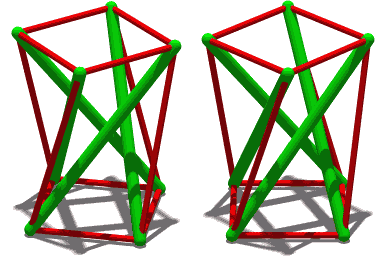
En liknande struktur men med fyra komprimeringselement.

Tensegritet , spänningsintegritet eller flytande kompression är en strukturell princip baserad på ett system av isolerade komponenter under kompression inuti ett nätverk av kontinuerlig spänning , och arrangerade på ett sådant sätt att de komprimerade delarna (vanligtvis stänger eller stag) inte vidrör varandra medan förspända spända delar (vanligtvis kablar eller senor) avgränsar systemet spatialt.

Termen myntades av Buckminster Fuller på 1960-talet som en portmanteau av "spänningsintegritet". Den andra benämningen av tensegrity, flytande kompression , användes främst av den konstruktivistiska konstnären Kenneth Snelson .

Begrepp

Tensegrity-strukturer är baserade på kombinationen av några enkla designmönster:

• element belastade i antingen ren kompression eller ren spänning, vilket innebär att strukturen bara kommer att gå sönder om kablarna ger efter eller stängerna bucklas. Detta gör att materialegenskaperna och tvärsnittsgeometrin för varje element kan optimeras för den speciella belastning den bär.
• förspänning eller spänningsförspänning tillåter kablar att alltid vara i spänning, för att bibehålla strukturell integritet.
• mekanisk stabilitet, vilket gör att delarna förblir i spänning/kompression när belastningen på strukturen ökar. Strukturen blir också styvare när kabelspänningen ökar.

På grund av dessa mönster upplever inget konstruktionselement ett böjmoment och det finns inga skjuvspänningar i systemet. Detta kan ge exceptionellt starka och styva strukturer för sin massa och för komponenternas tvärsnitt. Belastningen av åtminstone några tensegritetsstrukturer orsakar ett auxetiskt svar och negativt Poisson-förhållande , t.ex. T3-prisma och 6-stags tensegrity icosahedron.

The Skylon at the Festival of Britain , 1951

En begreppsmässig byggsten av spänning ses i 1951 års Skylon . Sex kablar , tre i varje ände, håller tornet på plats. De tre kablarna som är anslutna till botten "definierar" dess placering. De andra tre kablarna håller det helt enkelt vertikalt.

En spänningsstruktur med tre spö (visas till höger) bygger på denna enklare struktur: ändarna på varje grön spö ser ut som toppen och botten av Skylon. Så länge som vinkeln mellan två kablar är mindre än 180° är stångens position väl definierad. Medan tre kablar är det minsta som krävs för stabilitet, kan ytterligare kablar anslutas till varje nod för estetiska ändamål eller för att bygga in ytterligare stabilitet. Till exempel använder Snelson's Needle Tower ett upprepat mönster byggt med hjälp av noder som är anslutna till 5 kablar vardera.

Eleanor Heartney pekar ut visuell transparens som en viktig estetisk egenskap hos dessa strukturer. Korkmaz et al. har hävdat att lätta tensegrity-strukturer är lämpliga för adaptiv arkitektur .

Ansökningar

Tensegrities såg ökad tillämpning inom arkitektur med början på 1960-talet, när Maciej Gintowt och Maciej Krasiński designade Spodek arenakomplex (i Katowice , Polen ), som en av de första större strukturerna som använde principen om tensegrity. Taket använder en lutande yta som hålls i schack av ett system av kablar som håller upp dess omkrets. Tensegrity-principer användes också i David Geigers Olympic Gymnastics Arena i Seoul (för sommar-OS 1988) och Georgia Dome (för sommar-OS 1996 ). Tropicana Field , hemmaplan för Tampa Bay Rays major league basebolllag, har också ett kupoltak som stöds av en stor spänningsstruktur.

Största tensegrity-bron i världen, Kurilpa Bridge – Brisbane

Den 4 oktober 2009 öppnade Kurilpa-bron över Brisbanefloden i Queensland, Australien . En multipelmast, kabelstagskonstruktion baserad på principerna om tensegrity, det är för närvarande världens största tensegrity-bro.

NASA :s Super Ball Bot är en tidig prototyp för att landa på en annan planet utan krockkudde och sedan vara mobil att utforska. Spänningsstrukturen ger strukturell följsamhet som absorberar landningsstötkrafter och rörelse appliceras genom att ändra kabellängder, 2014.

Sedan början av 2000-talet har spänningar också väckt intresse hos robotister på grund av deras potential att designa lätta och motståndskraftiga robotar. Många undersökningar har undersökt tensegrity rovers, bio-härmande robotar och modulära mjuka robotar. Den mest kända tensegrity-roboten är Super Ball Bot , en rover för rymdutforskning med en 6-bar tensegrity-struktur, som för närvarande utvecklas på NASA Ames .

Biologi

Biotensegrity, en term som myntats av Dr. Stephen Levin, är en utökad teoretisk tillämpning av tensegrity-principer på biologiska strukturer. Biologiska strukturer såsom muskler , ben , fascia , ligament och senor , eller stela och elastiska cellmembran , görs starka genom samverkan av spända och komprimerade delar. Muskuloskeletala systemet består av ett kontinuerligt nätverk av muskler och bindväv, medan benen ger diskontinuerligt kompressionsstöd, medan nervsystemet upprätthåller spänningar in vivo genom elektrisk stimulans. Levin hävdar att den mänskliga ryggraden också är en tensegritetsstruktur även om det inte finns något stöd för denna teori ur ett strukturellt perspektiv.

Donald E. Ingber har utvecklat en teori om tensegrity för att beskriva många fenomen som observerats inom molekylärbiologin . Till exempel kan cellers uttryckta former, oavsett om det är deras reaktioner på applicerat tryck, interaktioner med substrat, etc., alla matematiskt modelleras genom att representera cellens cytoskelett som en tensegritet. Dessutom kan geometriska mönster som finns i hela naturen ( DNA :s spiral , den geodetiska kupolen på en volvox , Buckminsterfulleren , och mer) också förstås baserat på tillämpningen av principerna för tensegrity på den spontana självsammansättningen av föreningar, proteiner och till och med organ . Denna uppfattning stöds av hur spännings-kompressionsinteraktionerna av tensegrity minimerar material som behövs för att bibehålla stabilitet och uppnå strukturell elasticitet, även om jämförelsen med inerta material inom en biologisk ram inte har någon allmänt accepterad premiss inom fysiologisk vetenskap. Därför naturliga urvalstryck sannolikt gynna biologiska system organiserade på ett spänningssatt sätt.

Som Ingber förklarar:

De spänningsbärande elementen i dessa strukturer – oavsett om det är Fullers kupoler eller Snelsons skulpturer – kartlägger de kortaste vägarna mellan intilliggande delar (och är därför per definition geodesiskt ordnade). Spännkrafter överför sig naturligt över det kortaste avståndet mellan två punkter, så delarna i en spänningsstruktur är exakt placerade för att bäst motstå påfrestningar. Av denna anledning erbjuder tensegritetsstrukturer maximal styrka.

Inom embryologi föreslog Richard Gordon att embryonala differentieringsvågor fortplantas av en "differentieringsorganell" där cytoskelettet är sammansatt i en bistabil tensegritetsstruktur vid den apikala änden av celler som kallas "celltillståndsdelaren".

Ursprung och konsthistoria

Kenneth Snelsons 1948 X-Module Design som förkroppsligad i en kolumn med två moduler

Ursprunget till tensegrity är kontroversiellt. Många traditionella strukturer, såsom kajaker med hud på ram och shōji , använder spännings- och kompressionselement på ett liknande sätt.

Den ryske konstnären Viatcheslav Koleichuk hävdade att idén om spänstighet först uppfanns av Kārlis Johansons (på ryska som tyska som Karl Ioganson) ( lv ), en sovjetisk avantgardekonstnär av lettisk härkomst, som bidrog med några verk till huvudutställningen av rysk konstruktivism 1921. Koleichuks påstående backades upp av Maria Gough för ett av verken på den konstruktivistiska utställningen 1921. Snelson har erkänt konstruktivisterna som inflytande för sitt arbete (fråga?). Den franske ingenjören David Georges Emmerich har också noterat hur Kārlis Johansons arbete (och industriella designidéer) verkade förutse spänningskoncept.

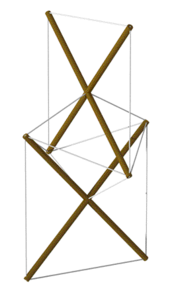
1948 producerade konstnären Kenneth Snelson sin innovativa "X-Piece" efter konstnärliga undersökningar vid Black Mountain College (där Buckminster Fuller föreläste) och på andra håll. Några år senare myntades termen "tensegrity" av Fuller, som är mest känd för sina geodetiska kupoler . Under hela sin karriär hade Fuller experimenterat med att införliva dragkomponenter i sitt arbete, till exempel i inramningen av sina dymaxionshus .

Snelsons innovation från 1948 sporrade Fuller att omedelbart beställa en mast från Snelson. 1949 utvecklade Fuller en tensegrity- ikosaeder baserad på tekniken, och han och hans elever utvecklade snabbt ytterligare strukturer och använde tekniken för att bygga kupoler. Efter ett uppehåll fortsatte Snelson också med att producera en uppsjö av skulpturer baserade på tensegrity-koncept. Hans huvudsakliga arbete började 1959 när en central utställning på Museum of Modern Art ägde rum. På MOMA-utställningen hade Fuller visat masten och några av hans andra verk. På denna utställning visade Snelson, efter en diskussion med Fuller och utställningsarrangörerna angående kreditering av masten, också en del verk i en vitrin .

Snelsons mest kända verk är hans 18 meter höga Needle Tower från 1968.

Stabilitet

Tensegrity prismor

Sträckningsstrukturen med tre stavar (3-vägs prisma) har egenskapen att för en given (gemensam) längd av kompressionselementets "stång" (det finns tre totalt) och en given (gemensam) längd av spänningskabeln "senan" ( sex totalt) för att koppla ihop stavändarna, finns det ett särskilt värde för den (gemensamma) längden på senan som förbinder stavtopparna med de närliggande stavbottnarna, vilket gör att strukturen håller en stabil form. För en sådan struktur är det enkelt att bevisa att triangeln som bildas av stavtopparna och den som bildas av stavbottnarna roteras i förhållande till varandra med en vinkel på 5π/6 (radianer).

Stabiliteten (”förspänningsbarheten”) hos flera 2-stegs tensegritetsstrukturer analyseras av Sultan et al.

T3-prismat (även känt som Triplex) kan erhållas genom att hitta ett rakt triangulärt prisma. Dess självjämviktstillstånd ges när bastrianglarna är i parallella plan åtskilda av en vridningsvinkel på π/6. Formeln för dess unika självstresstillstånd ges av,

$$\omega =\omega _{1}[-{\sqrt {(}}3),-{\sqrt {(}}3),-{\sqrt {(}}3),{\sqrt {(}}3) ,{\sqrt {(}}3),{\sqrt {(}}3),1,1,1,1,1,1]^{T}$$

Här motsvarar de tre första negativa värdena de inre komponenterna i kompression, medan resten motsvarar kablarna i spänning.

Tensegrity icosahedra

Matematisk modell av tensegrity icosahedron

Olika former av tensegrity icosahedra, beroende på förhållandet mellan längderna på senor och strävor.

En tensegrity ikosaeder gjord av sugrör och snöre

Tensegrity icosahedron , som först studerades av Snelson 1949, har strävor och senor längs kanterna på en polyeder som kallas Jessens icosahedron . Det är en stabil konstruktion, om än med oändlig rörlighet. För att se detta, överväg en kub med sidolängden 2 d , centrerad vid origo. Placera ett stag med längden 2 l i planet för varje kubyta, så att varje stag är parallellt med ena kanten av ytan och centreras på ytan. Dessutom bör varje stag vara parallellt med staget på den motsatta sidan av kuben, men ortogonalt mot alla andra stag. Om de kartesiska koordinaterna för en sträva är $(0,d,l)$ och $(0,d,-l)$ , de för dess parallella strut kommer att vara respektive $(0,-d,-l)$ och $(0,-d,l)$ . Koordinaterna för de andra strävändarna (hörn) erhålls genom att permutera koordinaterna, t.ex. $(0,d,l)\ högerpil (d,l,0)\högerpil (l,0,d)$ (rotationssymmetri i kubens huvuddiagonal).

Avståndet s mellan två valfria angränsande hörn (0, d , l ) och ( d , l , 0) är

$$s^{2}=(dl)^{2}+d^{ 2}+l^{2}=2\vänster(d-{\frac {1}{2}}\,l\höger)^{2}+{\frac {3}{2}}\,l^ {2}$$

Föreställ dig denna figur byggd av strävor med en given längd 2 l och senor (förbinder angränsande hörn) med given längd s , med $s>{\sqrt {\frac {3}{2}}}\, l$ . Relationen säger oss att det finns två möjliga värden för d : ett realiserat genom att trycka ihop strävorna, det andra genom att dra isär dem. I det speciella fallet $s={\sqrt {\frac {3}{2}}}\,l$ sammanfaller de två ytterligheterna, och $d={\ frac {1}{2}}\,l$ , därför är figuren den stabila tensegrity ikosaedern. Detta val av parametrar ger hörn positionerna för Jessens ikosaeder; de skiljer sig från den vanliga ikosaedern , för vilken förhållandet mellan $d$ och $l$ skulle vara det gyllene snittet snarare än 2. Båda uppsättningarna av koordinater ligger dock längs en kontinuerlig familj av positioner som sträcker sig från kuboktaedern till oktaedern (som gränsfall), vilka är kopplade genom en spiralformad kontraktiv/expansiv transformation . Denna kinematik för kuboktaedern är rörelsegeometrin för tensegrity icosahedron. Det beskrevs först av HSM Coxeter och kallades senare för "jitterbug-transformationen" av Buckminster Fuller.

Eftersom tensegrity icosahedron representerar en extrempunkt av ovanstående relation, har den oändlig rörlighet: en liten förändring i senan s längd (t.ex. genom att sträcka senor) resulterar i en mycket större förändring av avståndet 2 d av strävorna.

Patent

• US-patent 3 063 521 , "Tensile-Integrity Structures", 13 november 1962, Buckminster Fuller.
• Franska patentet nr 1 377 290, "Construction de Reseaux Autotendants", 28 september 1964, David Georges Emmerich.
• Franska patentet nr 1 377 291, "Structures Linéaires Autotendants", 28 september 1964, David Georges Emmerich.
• US-patent 3 139 957 , "Suspension Building" (även kallad aspension), 7 juli 1964, Buckminster Fuller.
• US-patent 3 169 611 , "Continuous Tension, Discontinuous Compression Structure", 16 februari 1965, Kenneth Snelson.
• US-patent 3 866 366 , "Non-symmetrical Tension-Integrity Structures", 18 februari 1975, Buckminster Fuller.

Grundläggande tensegritetsstrukturer

• 

  Den enklaste tensegrity-strukturen, ett 3-prisma

• 

  Ännu en 3-prisma

• 

  En liknande struktur men med fyra kompressionselement

• 

  Proto-Tensegrity Prism av Karl Ioganson , 1921

• 

  Tensegrity Icosahedron, Buckminster Fuller , 1949

• 

  Tensegrity Tetrahedron, Francesco della Salla, 1952

• 

  Tensegrity X-Module Tetrahedron, Kenneth Snelson , 1959

Tensegritetsstrukturer

• 

  Kenneth Snelsons nåltorn konstskulptur.

• 

  En tensegrity-kupol gjord av trädgårdspålar och nylongarn byggd på gården till ett hus, 2009

• 

  En 12 meter hög strukturutställning i Science City , Kolkata .

• 

  Dissipate , en konstskulptur i timglastorn inklusive tensegrity-struktur, konstruerad på AfrikaBurn 2015, ett regionalt evenemang i Burning Man

Se även

• Cloud Nine – föreslagna luftburna livsmiljöer skapade av gigantiska geodetiska sfärer Sidor som visar wikidata-beskrivningar som en reserv , gigantiska skyssvävande tensegrity-sfärer namngivna av Buckminster Fuller
• Hyperboloid struktur – Typ av ogränsad kvadratisk ytformad byggnad eller verk
• Interaktioner av aktörer teori
• Sadeltak – typ av takkonstruktion Sidor som visar wikidata-beskrivningar som reserv
• Rymdram – Styv tredimensionell lastbärande fackverkskonstruktion
• Synergetics – En skola för empiriska studier av systembeteende föreslagit av Buckminster Fuller Pages som visar wikidata-beskrivningar som en reserv
• Tensairitet
• Dragstruktur – konstruktion av element som endast bär spänning och ingen kompression eller böjning Sidor som visar wikidata-beskrivningar som en reserv
• Tunnskalsstruktur – strukturelement i solid mekanik Sidor som visar wikidata-beskrivningar som en reserv
• Kuboktaederns kinematik – Symmetriska omvandlingar av kuboktaedern till relaterade enhetliga polyedrar, geometrin för rörelsen hos tensegrity ikosaedern

Bibliografi

• Fuller, R. Buckminster (1961). "Tensegrity" . Portfolio and Art News Annual (4): 112–127, 144, 148.
•   — (1982) [1975]. Synergetik: Explorations in the Geometry of Thinking . Vol. I. Macmillan. ISBN 978-0-02-065320-2 .
•   — (1983) [1979]. Synergetics 2: Ytterligare undersökningar i tänkandets geometri . Vol. 2. Macmillan. ISBN 978-0-02-092640-5 . Uppkopplad
•   —; Marks, Robert W. (1973) [1960]. The Dymaxion World of Buckminster Fuller . Ankare böcker. FIG. 261–280. ISBN 978-0385018043 . En bra översikt över omfattningen av tensegrity ur Fullers synvinkel, och en intressant översikt över tidiga strukturer med noggranna tillskrivningar för det mesta.
•    Kenner, Hugh (1976). Geodesisk matematik och hur man använder den . University of California Press. ISBN 978-0520029248 . 2003 nytryck ISBN 0520239318 . Detta är en bra utgångspunkt för att lära sig om matematiken kring tensegrity och bygga modeller.
•   Gómez-Jáuregui, Valentin (2007). Tensegridad. Estructuras Tensegríticas en Ciencia y Arte (på spanska). Santander: Universidad de Cantabria. ISBN 978-84-8102-437-1 .
•   — (2010). Tensegritetsstrukturer och deras tillämpning på arkitektur . Santander: Servicio de Publicaciones de la Universidad de Cantabria. ISBN 978-84-8102-575-0 .
•   Gough, Maria (våren 1998). "I konstruktivismens laboratorium: Karl Iogansons kalla strukturer". oktober . 84 : 90–117. doi : 10.2307/779210 . JSTOR 779210 .
•   Juan, SJ; Tur, JM (juli 2008). "Tensegrity frameworks: Static analysis review". Mekanism och maskinteori . 43 (7): 859–81. CiteSeerX 10.1.1.574.7510 . doi : 10.1016/j.mechmachtheory.2007.06.010 .
•   Korkmaz, Sinan; Bel Hadj Ali, Nizar; Smith, Ian FC (juni 2011). "Bestämma kontrollstrategier för skadetolerans för en aktiv tensegrity-struktur" ( PDF) . Tekniska strukturer . 33 (6): 1930–1939. CiteSeerX 10.1.1.370.6243 . doi : 10.1016/j.engstruct.2011.02.031 . Arkiverad från originalet (PDF) den 29 september 2011.
• —; —; — (januari 2012). "Konfiguration av kontrollsystem för skadetolerans för en tensegrity-bro" . Avancerad teknisk informatik . 26 (1): 145–155. doi : 10.1016/j.aei.2011.10.002 .
•   Lavani, Haresh, red. (1996). "Origins of Tensegrity: Views of Emmerich, Fuller and Snelson" . International Journal of Space Structures . 11 (1–2): 27–55. doi : 10.1177/026635119601-204 . S2CID 114004009 .
•   Souza, Thales R.; Fonseca, Sérgio T.; Gonçalves, Gabriela G.; Ocarino, Juliana M.; Mancini, Marisa C. (oktober 2009). "Förspänning avslöjas av passiv samspänning i fotleden" . Journal of Biomechanics . 42 (14): 2374–80. doi : 10.1016/j.jbiomech.2009.06.033 . PMID 19647832 .

Vidare läsning

• Edmondson, Amy (2007). "En fullständigare förklaring" , Emergent World LLC
•   Forbes, Peter (2010) [2006]. "9. Push and Pull Building System" . Geckos fot: hur forskare tar ett blad från naturens bok . Harper Collins. s. 197–230. ISBN 978-0-00-740547-3 .
•   Hanaor, Ariel (1997). "13. Tensegrity: Teori och tillämpning" . I Gabriel, J. François (red.). Beyond the Cube: The Architecture of Space Frames and Polyhedra . Wiley. s. 385–408. ISBN 978-0-471-12261-6 .
• Masic, Milenko; Skelton, Robert E.; Gill, Philip E. (augusti 2005). "Algebraisk tensegrity form-finding". International Journal of Solids and Structures . 42 (16–17): 4833–4858. doi : 10.1016/j.ijsolstr.2005.01.014 . De presenterar det anmärkningsvärda resultatet att varje linjär transformation av en tensegritet också är en tensegrity.
•   Morgan, GJ (2003). "Historisk granskning: virus, kristaller och geodetiska kupoler". Trender inom biokemiska vetenskaper . 28 (2): 86–90. doi : 10.1016/S0968-0004(02)00007-5 . PMID 12575996 .
•   Motro, R. (1992). "Tensegrity Systems: The State of the Art". International Journal of Space Structures . 7 (2): 75–84. doi : 10.1177/026635119200700201 . S2CID 107820090 .
•   Pugh, Anthony (1976). En introduktion till Tensegrity . University of California Press. ISBN 978-0-520-03055-8 . Arkiverad från originalet den 4 maj 2008 . Hämtad 9 maj 2008 .
• Snelson, Kenneth (november 1990). "Brev till R. Motro" . International Journal of Space Structures .
• Vilnay, Oren (1990). Cable Nets and Tensegric Shells: Analysis and Design Applications , New York: Ellis Horwood Ltd.
• Wang, Bin-Bing (1998). "Cable-strut systems: Part I - Tensegrity". Journal of Constructional Steel Research . 45 (3): 281–89. doi : 10.1016/S0143-974X(97)00075-8 .
• Wilken, Timothy (2001). Seking the Gift Tensegrity , TrustMark

externa länkar

• Vetenskapliga publikationer i området för tensegrity av Schweiziska Federal Institute of Technology (EPFL), Applied Computing and Mechanics Laboratory (IMAC)
• Stephen Levins Biotensegrity-webbplats Flera artiklar om tensegrity-mekaniken hos biologiska strukturer från virus till ryggradsdjur av en ortopedisk kirurg.