Reduktion av icke-linjär dimensionalitet

Överst till vänster: en 3D-datauppsättning med 1000 punkter i ett spiralband (alias Swiss Roll ) med ett rektangulärt hål i mitten. Överst till höger: det ursprungliga 2D-grenröret som används för att generera 3D-datauppsättningen. Nederst till vänster och höger: 2D-återställning av grenröret med hjälp av LLE- och Hessian LLE- algoritmerna som implementeras av verktygssatsen Modular Data Processing.

Icke-linjär dimensionalitetsreduktion , även känd som manifold learning , hänvisar till olika relaterade tekniker som syftar till att projicera högdimensionell data på lägre dimensionella latenta manifolds , med målet att antingen visualisera data i det lågdimensionella rummet, eller lära sig kartläggningen ( antingen från det högdimensionella utrymmet till den lågdimensionella inbäddningen eller vice versa). Teknikerna som beskrivs nedan kan förstås som generaliseringar av linjära nedbrytningsmetoder som används för dimensionalitetsreduktion , såsom singularvärdesupplösning och principal komponentanalys .

Tillämpningar av NLDR

Betrakta en datauppsättning representerad som en matris (eller en databastabell), så att varje rad representerar en uppsättning attribut (eller egenskaper eller dimensioner) som beskriver en viss instans av något. Om antalet attribut är stort, är utrymmet för unika möjliga rader exponentiellt stort. Således, ju större dimensionalitet, desto svårare blir det att ta prov på utrymmet. Detta orsakar många problem. Algoritmer som arbetar på högdimensionell data tenderar att ha en mycket hög tidskomplexitet. Många maskininlärningsalgoritmer kämpar till exempel med högdimensionell data. Att reducera data till färre dimensioner gör ofta analysalgoritmer effektivare och kan hjälpa maskininlärningsalgoritmer att göra mer exakta förutsägelser.

Människor har ofta svårt att förstå data i höga dimensioner. Därför är det användbart att reducera data till ett litet antal dimensioner för visualiseringsändamål.

Rita av de tvådimensionella punkter som är resultatet av att använda en NLDR-algoritm. I det här fallet används Manifold Sculpting för att reducera data till bara två dimensioner (rotation och skala).

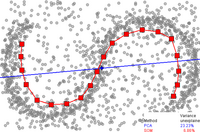
De reducerade dimensionella representationerna av data kallas ofta för "inneboende variabler". Denna beskrivning antyder att det är dessa värden som data producerades från. Tänk till exempel på en datauppsättning som innehåller bilder med bokstaven "A", som har skalats och roterats i olika mängder. Varje bild har 32×32 pixlar. Varje bild kan representeras som en vektor med 1024 pixelvärden. Varje rad är ett prov på ett tvådimensionellt grenrör i ett 1024-dimensionellt utrymme (ett Hamming-utrymme ) . Den inneboende dimensionaliteten är två, eftersom två variabler (rotation och skala) varierades för att producera data. Information om formen eller utseendet på en bokstav 'A' är inte en del av de inneboende variablerna eftersom den är densamma i alla fall. Icke-linjär dimensionalitetsreduktion förkastar den korrelerade informationen (bokstaven 'A') och återställer endast den varierande informationen (rotation och skala). Bilden till höger visar exempelbilder från denna datauppsättning (för att spara utrymme visas inte alla indatabilder) och en plot av de tvådimensionella punkterna som är resultatet av att använda en NLDR-algoritm (i det här fallet användes Manifold Sculpting) för att reducera data till bara två dimensioner.

PCA (en linjär dimensionsreduktionsalgoritm) används för att reducera samma datauppsättning till två dimensioner, de resulterande värdena är inte så välorganiserade.

Som jämförelse, om principal komponentanalys , som är en linjär dimensionsreduktionsalgoritm, används för att reducera samma datauppsättning till två dimensioner, är de resulterande värdena inte så välorganiserade. Detta visar att de högdimensionella vektorerna (var och en representerar en bokstav 'A') som samplar detta grenrör varierar på ett icke-linjärt sätt.

Det bör därför vara uppenbart att NLDR har flera tillämpningar inom området datorseende. Tänk till exempel på en robot som använder en kamera för att navigera i en sluten statisk miljö. Bilderna som erhålls med den kameran kan anses vara prover på ett grenrör i högdimensionellt utrymme, och de inneboende variablerna för det grenröret kommer att representera robotens position och orientering.

Invarianta grenrör är av allmänt intresse för modellorderminskning i dynamiska system . I synnerhet, om det finns ett attraherande invariant grenrör i fasutrymmet, kommer närliggande banor att konvergera till det och stanna på det på obestämd tid, vilket gör det till en kandidat för dimensionalitetsreduktion av det dynamiska systemet. Även om sådana grenrör inte garanteras existerar i allmänhet, ger teorin om spektrala undergrenar (SSM) förutsättningar för existensen av unika attraherande invarianta objekt i en bred klass av dynamiska system. Aktiv forskning inom NLDR strävar efter att utveckla de observationsgrenrör som är förknippade med dynamiska system för att utveckla modelleringstekniker.

Några av de mer framträdande teknikerna för minskning av olinjär dimensionalitet listas nedan.

Viktiga begrepp

Sammons kartläggning

Sammons kartläggning är en av de första och mest populära NLDR-teknikerna.

Approximation av en huvudkurva med endimensionell SOM (en streckad linje med röda rutor, 20 noder). Den första huvudkomponenten presenteras av en blå rak linje. Datapunkter är de små grå cirklarna. För PCA är den oförklarade variansfraktionen i detta exempel 23,23 %, för SOM är den 6,86 %.

Självorganiserande karta

Den självorganiserande kartan (SOM, även kallad Kohonen-karta ) och dess probabilistiska variant generativ topografisk kartläggning (GTM) använder en punktrepresentation i det inbäddade rummet för att bilda en latent variabelmodell baserad på en icke-linjär avbildning från det inbäddade rummet till det inbäddade rummet. högdimensionellt utrymme. Dessa tekniker är relaterade till arbete med täthetsnätverk, som också är baserade på samma probabilistiska modell.

Analys av kärnans huvudkomponent

Den kanske mest använda algoritmen för dimensionsreduktion är kärnan PCA . PCA börjar med att beräkna kovariansmatrisen för $m\times n$ matrisen $\mathbf {X}$

$C={\frac {1}{m}}\sum _{i=1}^{m}{\mathbf {x} _{i}\mathbf {x} _{i}^{\mathsf {T}}}.$

Den projicerar sedan data på de första k egenvektorerna i den matrisen. Som jämförelse börjar KPCA med att beräkna kovariansmatrisen för data efter att ha transformerats till ett högre dimensionellt utrymme,

$C={\frac {1}{m}}\sum _{i=1}^{m}{\Phi (\mathbf {x} _{i})\Phi (\mathbf {x} _ {i})^{\mathsf {T}}}.$

Den projicerar sedan den transformerade datan på de första k egenvektorerna i den matrisen, precis som PCA. Den använder kärntricket för att faktorisera bort mycket av beräkningen, så att hela processen kan utföras utan att faktiskt beräkna $\Phi (\mathbf {x} )$ . Naturligtvis $\Phi$ väljas så att den har en känd motsvarande kärna. Tyvärr är det inte trivialt att hitta en bra kärna för ett givet problem, så KPCA ger inte bra resultat med vissa problem när man använder standardkärnor. Till exempel är det känt att prestera dåligt med dessa kärnor på Swiss Roll- grenröret. Man kan dock se vissa andra metoder som fungerar bra i sådana inställningar (t.ex. Laplacian Eigenmaps, LLE) som speciella fall av kärn-PCA genom att konstruera en databeroende kärnmatris.

KPCA har en intern modell, så den kan användas för att kartlägga punkter på dess inbäddning som inte var tillgängliga vid träningstillfället.

Huvudkurvor och grenrör

Tillämpning av huvudkurvor: Icke-linjärt livskvalitetsindex. Poäng representerar data från FN:s 171 länder i 4-dimensionellt rymden bildad av värdena för 4 indikatorer: bruttoprodukt per capita , förväntad livslängd , spädbarnsdödlighet , tuberkulosförekomst . Olika former och färger motsvarar olika geografiska platser. Röd fet linje representerar huvudkurvan och approximerar datasetet. Denna huvudkurva producerades med metoden för elastisk karta . Programvaran är tillgänglig för fri icke-kommersiell användning.

Huvudkurvor och grenrör ger det naturliga geometriska ramverket för minskning av icke-linjär dimensionalitet och utökar den geometriska tolkningen av PCA genom att explicit konstruera ett inbäddat grenrör och genom att koda med standard geometrisk projektion på grenröret. Detta tillvägagångssätt föreslogs ursprungligen av Trevor Hastie i sin avhandling från 1984, som han formellt introducerade 1989. Denna idé har utforskats ytterligare av många författare. Hur man definierar grenrörets "enkelhet" är problemberoende, men det mäts vanligtvis av grenrörets inneboende dimensionalitet och/eller jämnheten. Vanligtvis definieras huvudgrenröret som en lösning på ett optimeringsproblem. Den objektiva funktionen inkluderar en kvalitetsuppskattning av data och vissa straffvillkor för böjning av grenröret. De populära initiala approximationerna genereras av linjär PCA och Kohonens SOM.

Laplacian egenkartor

Se även: Manifold regularization

Laplacian egenkartor använder spektraltekniker för att utföra dimensionsreduktion. Denna teknik bygger på det grundläggande antagandet att data ligger i ett lågdimensionellt grenrör i ett högdimensionellt utrymme. Denna algoritm kan inte bädda in punkter utanför samplingen, men tekniker baserade på reproducering av kärnan Hilbert-utrymmesregularisering finns för att lägga till denna förmåga. Sådana tekniker kan också tillämpas på andra icke-linjära dimensionsreduktionsalgoritmer.

Traditionella tekniker som huvudkomponentanalys tar inte hänsyn till datas inneboende geometri. Laplacian egenkartor bygger en graf från grannskapsinformation för datamängden. Varje datapunkt fungerar som en nod på grafen och anslutningen mellan noder styrs av närheten till angränsande punkter (med användning av t.ex. k- närmaste granne-algoritmen ). Den sålunda genererade grafen kan betraktas som en diskret approximation av det lågdimensionella grenröret i det högdimensionella rummet. Minimering av en kostnadsfunktion baserad på grafen säkerställer att punkter nära varandra på grenröret kartläggs nära varandra i det lågdimensionella rummet, vilket bevarar lokala avstånd. Egenfunktionerna för Laplace-Beltrami-operatorn på grenröret fungerar som inbäddningsdimensioner, eftersom denna operator under milda förhållanden har ett räknebart spektrum som är en grund för kvadratintegrerbara funktioner på grenröret (jämför Fourier-serien på enhetscirkelgrenröret). Försök att placera Laplacian egenkartor på solid teoretisk grund har mött viss framgång, eftersom under vissa icke-restriktiva antaganden har grafen Laplacian matris visat sig konvergera till Laplace-Beltrami-operatorn när antalet punkter går till oändlighet.

Isomap

Isomap är en kombination av Floyd–Warshall-algoritmen med klassisk Multidimensional Scaling . Classic Multidimensional Scaling (MDS) tar en matris med parvisa avstånd mellan alla punkter och beräknar en position för varje punkt. Isomap antar att de parvisa avstånden endast är kända mellan närliggande punkter, och använder Floyd-Warshall-algoritmen för att beräkna de parvisa avstånden mellan alla andra punkter. Detta uppskattar effektivt hela matrisen av parvisa geodetiska avstånd mellan alla punkter. Isomap använder sedan klassisk MDS för att beräkna de reducerade dimensionella positionerna för alla punkter. Landmark-Isomap är en variant av denna algoritm som använder landmärken för att öka hastigheten, till priset av viss noggrannhet.

Vid grenrörsinlärning antas ingångsdata vara samplade från ett lågdimensionellt grenrör som är inbäddat i ett vektorrum med högre dimensioner. Den huvudsakliga intuitionen bakom MVU är att utnyttja den lokala linjäriteten hos grenrören och skapa en kartläggning som bevarar lokala kvarter vid varje punkt i det underliggande grenröret.

Lokalt linjär inbäddning

Locally-linear Embedding (LLE) presenterades ungefär samtidigt som Isomap. Den har flera fördelar jämfört med Isomap, inklusive snabbare optimering när den implementeras för att dra fördel av glesa matrisalgoritmer , och bättre resultat med många problem. LLE börjar också med att hitta en uppsättning av de närmaste grannarna till varje punkt. Den beräknar sedan en uppsättning vikter för varje punkt som bäst beskriver punkten som en linjär kombination av dess grannar. Slutligen använder den en egenvektorbaserad optimeringsteknik för att hitta den lågdimensionella inbäddningen av punkter, så att varje punkt fortfarande beskrivs med samma linjära kombination av sina grannar. LLE tenderar att hantera olikformiga provdensiteter dåligt eftersom det inte finns någon fast enhet för att förhindra att vikterna glider eftersom olika regioner skiljer sig i provdensiteter. LLE har ingen intern modell.

LLE beräknar de barycentriska koordinaterna för en punkt Xi _baserat på dess grannar Xj _. Den ursprungliga punkten rekonstrueras av en linjär kombination, given av viktmatrisen Wij _, av dess grannar. Rekonstruktionsfelet ges av kostnadsfunktionen E ( W ).

$E(W)=\summa _{i}\left|\mathbf {X} _{i}-\summa _{j}{\mathbf {W} _{ij}\mathbf {X} _ {j}}\right|^{2}$

Vikterna W _ij hänvisar till mängden bidrag som punkten _Xj har vid rekonstruktion _av punkten Xi . Kostnadsfunktionen minimeras under två begränsningar: (a) Varje datapunkt _X i _{rekonstrueras} endast från sina grannar, vilket tvingar _Wij att vara noll om punkt Xj inte är en granne till punkten X _i och (b) Summan av varje rad i viktmatrisen är lika med 1.

$\sum _{j}{\mathbf {W} _{ij}}=1$

De ursprungliga datapunkterna samlas in i ett D- dimensionellt utrymme och målet med algoritmen är att reducera dimensionaliteten till d så att D >> d . Samma vikter W _ij som rekonstruerar den i: te datapunkten i det D -dimensionella utrymmet kommer att användas för att rekonstruera samma punkt i det lägre d- dimensionella utrymmet. En stadsvårdskarta skapas utifrån denna idé. Varje punkt Xi _i det dimensionella D -utrymmet mappas till en punkt Yi _i det d- dimensionella rummet genom att minimera kostnadsfunktionen

$C(Y)=\summa _{i}\left|\mathbf {Y} _{i}-\summa _{j}{\mathbf {W} _{ij}\mathbf {Y} _ {j}}\right|^{2}$

, hålls vikterna W _{ij fasta och minimeringen görs på punkterna Y i} för att optimera koordinaterna. Detta minimeringsproblem kan lösas genom att lösa ett sparsamt N X N -egenvärdeproblem ( N är antalet datapunkter), vars botten d icke-nollegenvektorer ger en ortogonal uppsättning koordinater. Generellt rekonstrueras datapunkterna från K närmaste grannar, mätt med euklidiskt avstånd . För en sådan implementering har algoritmen endast en fri parameter K, som kan väljas genom korsvalidering.

Hessisk lokalt-linjär inbäddning (hessisk LLE)

Liksom LLE är även Hessian LLE baserad på glesa matristekniker. Det tenderar att ge resultat av mycket högre kvalitet än LLE. Tyvärr har den en mycket kostsam beräkningskomplexitet, så den är inte väl lämpad för kraftigt samplade grenrör. Den har ingen intern modell.

Modifierad lokalt-linjär inbäddning (MLLE)

Modifierad LLE (MLLE) är en annan LLE-variant som använder flera vikter i varje grannskap för att lösa det lokala viktmatriskonditioneringsproblemet som leder till förvrängningar i LLE-kartor. Löst sett är de multipla vikterna den lokala ortogonala projektionen av de ursprungliga vikterna som produceras av LLE. Skaparna av denna reguljära variant är också författarna till Local Tangent Space Alignment (LTSA), som är implicit i MLLE-formuleringen när man inser att den globala optimeringen av de ortogonala projektionerna för varje viktvektor, i huvudsak justerar de lokala tangentrymden av varje datapunkt. De teoretiska och empiriska implikationerna från korrekt tillämpning av denna algoritm är långtgående.

Lokal tangentrymdsjustering

Huvudartikel: Lokal tangentrymdsjustering

LTSA är baserad på intuitionen att när ett grenrör är korrekt utvikt kommer alla tangenthyperplanen till grenröret att bli inriktade. Det börjar med att beräkna k- närmaste grannar för varje punkt. Den beräknar tangentrymden vid varje punkt genom att beräkna de d -första huvudkomponenterna i varje lokal grannskap. Den optimerar sedan för att hitta en inbäddning som justerar tangentutrymmena.

Maximal varians utvecklas

Maximal Variance Unfolding , Isomap och Locally Linear Embedding delar en gemensam intuition som förlitar sig på föreställningen att om ett grenrör är korrekt utvikt, så maximeras variansen över punkterna. Dess första steg, som Isomap och Locally Linear Embedding, är att hitta de k -närmaste grannarna till varje punkt. Den försöker sedan lösa problemet med att maximera avståndet mellan alla icke-angränsande punkter, begränsade så att avstånden mellan angränsande punkter bevaras. Det primära bidraget från denna algoritm är en teknik för att gjuta detta problem som ett semidefinitivt programmeringsproblem. Tyvärr har semidefinite programmeringslösare en hög beräkningskostnad. Liksom Locally Linear Embedding har den ingen intern modell.

Autokodare

En autoencoder är ett neuralt nätverk för feed-forward som är tränat för att approximera identitetsfunktionen. Det vill säga, den är tränad att mappa från en vektor med värden till samma vektor. När det används för dimensionsminskningsändamål är ett av de dolda lagren i nätverket begränsat till att endast innehålla ett litet antal nätverksenheter. Nätverket måste alltså lära sig att koda vektorn till ett litet antal dimensioner och sedan avkoda den tillbaka till det ursprungliga utrymmet. Således är den första halvan av nätverket en modell som kartlägger från högdimensionellt till lågdimensionell rymd, och den andra halvan kartlägger från lågdimensionell till högdimensionell rymd. Även om idén med autoencoders är ganska gammal, har utbildning av djupa autoencoders först nyligen blivit möjlig genom användningen av begränsade Boltzmann-maskiner och staplade autoencoders. Relaterad till autokodare är NeuroScale-algoritmen, som använder stressfunktioner inspirerade av flerdimensionell skalning och Sammon-mappningar (se ovan) för att lära sig en icke-linjär mappning från det högdimensionella till det inbäddade rummet. Mappningarna i NeuroScale är baserade på radiella basfunktionsnätverk .

Gaussiska process latenta variabelmodeller

Gaussiska process latenta variabelmodeller (GPLVM) är probabilistiska dimensionsreduktionsmetoder som använder Gaussiska processer (GPs) för att hitta en lägre dimensionell icke-linjär inbäddning av högdimensionell data. De är en förlängning av den probabilistiska formuleringen av PCA. Modellen definieras probabilistiskt och de latenta variablerna marginaliseras sedan och parametrar erhålls genom att maximera sannolikheten. Liksom kärn-PCA använder de en kärnfunktion för att bilda en icke-linjär mappning (i form av en Gauss-process) . Men i GPLVM är mappningen från det inbäddade (latenta) utrymmet till datautrymmet (som täthetsnätverk och GTM) medan det i kärnan PCA är i motsatt riktning. Det föreslogs ursprungligen för visualisering av högdimensionella data men har utökats för att konstruera en delad mångfaldig modell mellan två observationsutrymmen. GPLVM och dess många varianter har föreslagits speciellt för mänsklig rörelsemodellering, t.ex. ryggbegränsad GPLVM, GP dynamisk modell (GPDM), balanserad GPDM (B-GPDM) och topologiskt begränsad GPDM. För att fånga kopplingseffekten av ställnings- och gångförgreningar i gånganalysen, föreslogs ett flerlagers ledgångsförgreningsrör.

t-fördelad stokastisk granninbäddning

t-distribuerad stokastisk granninbäddning (t-SNE) används ofta. Det är en av en familj av stokastiska granninbäddningsmetoder. Algoritmen beräknar sannolikheten för att par av datapunkter i det högdimensionella rymden är relaterade, och väljer sedan lågdimensionella inbäddningar som ger en liknande fördelning.

Andra algoritmer

Relationsperspektivkarta

Relationsperspektivkarta är en flerdimensionell skalningsalgoritm . Algoritmen hittar en konfiguration av datapunkter på ett grenrör genom att simulera ett dynamiskt multipartikelsystem på ett slutet grenrör, där datapunkter mappas till partiklar och avstånd (eller olikheter) mellan datapunkter representerar en frånstötande kraft. När grenröret gradvis växer i storlek kyls flerpartikelsystemet gradvis och konvergerar till en konfiguration som återspeglar avståndsinformationen för datapunkterna.

Relationell perspektivkarta var inspirerad av en fysisk modell där positivt laddade partiklar rör sig fritt på ytan av en boll. Styrd av Coulomb -kraften mellan partiklarna, kommer den minimala energikonfigurationen av partiklarna att återspegla styrkan hos frånstötande krafter mellan partiklarna.

Den relationella perspektivkartan introducerades i. Algoritmen använde först den platta torusen som bildgrenröret, sedan har den utökats (i programvaran VisuMap för att använda andra typer av slutna grenrör, som sfären , projektivt utrymme och Klein-flaskan , som bildförgreningar.

Smittkartor

Smittningskartor använder flera smittor på ett nätverk för att kartlägga noderna som ett punktmoln. I fallet med Global Cascades-modellen kan spridningshastigheten justeras med tröskelparametern $t\in [0,1]$ . För $t=0$ är spridningskartan ekvivalent med Isomap -algoritmen.

Kurvilinjär komponentanalys

Curvilinear component analysis (CCA) letar efter konfigurationen av punkter i utgångsutrymmet som bevarar ursprungliga avstånd så mycket som möjligt samtidigt som man fokuserar på små avstånd i utgångsutrymmet (omvänt till Sammons mappning som fokuserar på små avstånd i det ursprungliga utrymmet).

Det bör noteras att CCA, som en iterativ inlärningsalgoritm, faktiskt börjar med fokus på stora avstånd (som Sammon-algoritmen), för att sedan gradvis ändra fokus till små avstånd. Informationen om små avstånd kommer att skriva över informationen om stora avstånd, om kompromisser mellan de två måste göras.

Stressfunktionen hos CCA är relaterad till summan av höger Bregman-divergenser.

Kurvilinjär avståndsanalys

CDA tränar ett självorganiserande neuralt nätverk för att passa grenröret och försöker bevara geodetiska avstånd i dess inbäddning. Den är baserad på Curvilinear Component Analysis (som utökade Sammons kartläggning), men använder istället geodetiska avstånd.

Reduktion av diffeomorf dimensionalitet

Diffeomorphic Dimensionality Reduction eller Diffeomap lär sig en smidig diffeomorf mappning som transporterar data till ett linjärt delrum med lägre dimensioner. Metoderna löser ett jämnt tidsindexerat vektorfält så att flöden längs fältet som börjar vid datapunkterna kommer att sluta vid ett lägre dimensionellt linjärt delrum, och försöker därigenom bevara parvisa skillnader under både framåt- och inversavbildningen.

Uppriktning av grenrör

Manifoldjustering drar fördel av antagandet att olika datamängder som produceras av liknande genereringsprocesser kommer att dela en liknande underliggande mångfaldsrepresentation. Genom att lära sig projektioner från varje originalutrymme till det delade mångfalden, återvinns korrespondenser och kunskap från en domän kan överföras till en annan. De flesta mångfaldiga inriktningstekniker beaktar endast två datamängder, men konceptet sträcker sig till godtyckligt många initiala datamängder.

Diffusionskartor

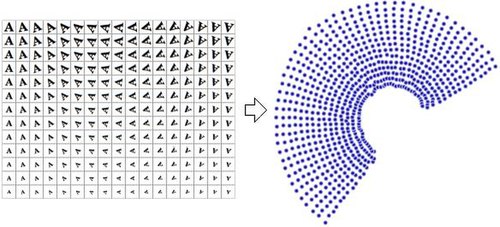
Diffusionskartor utnyttjar förhållandet mellan värmediffusion och en slumpmässig promenad ( Markov Chain) ; en analogi dras mellan diffusionsoperatorn på ett grenrör och en Markov-övergångsmatris som arbetar på funktioner definierade på grafen vars noder samplades från grenröret. Låt särskilt en datamängd representeras av $\mathbf {X} =[x_{1},x_{2},\ ldots ,x_{n}]\in \Omega \subset \mathbf {R^{D}}$ . Det underliggande antagandet av diffusionskarta är att högdimensionella data ligger på ett lågdimensionellt grenrör med dimension $\mathbf {d}$ . Låt X representera datamängden och $\mu$ representera fördelningen av datapunkterna på X . Definiera vidare en kärna som representerar någon föreställning om affinitet för punkterna i X. Kärnan ${\mathit {k}}$ har följande egenskaper

$k(x,y)=k(y,x),$

k är symmetrisk

$k(x,y)\geq 0\qquad \forall x,y,k$

k är positivitetsbevarande

Således kan man tänka på de individuella datapunkterna som noderna i en graf och kärnan k som definierar någon sorts affinitet på den grafen. Grafen är symmetrisk till sin konstruktion eftersom kärnan är symmetrisk. Det är lätt att se här att man från tupeln ( X , k ) kan konstruera en vändbar Markovkedja . Denna teknik är gemensam för en mängd olika områden och är känd som grafen Laplacian.

Till exempel kan grafen K = ( X , E ) konstrueras med hjälp av en gaussisk kärna.

$K_{ij}={\begin{cases}e^{-\|x_{i} -x_{j}\|_{2}^{2}/\sigma ^{2}}&{\text{if }}x_{i}\sim x_{j}\\0&{\text{annars} }\end{cases}}$

I ovanstående ekvation anger ${\displaystyle x_{i}\sim x_{j}} att$$x_{i}$ är närmaste granne till $x_{j}$ . Geodesiskt avstånd bör korrekt användas för att faktiskt mäta avstånd på grenröret . Eftersom den exakta strukturen för grenröret inte är tillgänglig, för de närmaste grannarna är det geodetiska avståndet approximerat med euklidiskt avstånd. Valet $\sigma$ modulerar vår uppfattning om närhet i den meningen att om $\|x_{i}-x_{j}\|_{2}\ gg \sigma$ då $K_{ij}=0$ och om $\|x_{i}-x_{j}\|_{2 }\ll \sigma$ sedan $K_{ij}=1$ . Det förra betyder att mycket lite diffusion har ägt rum medan det senare innebär att diffusionsprocessen är nästan avslutad. Olika strategier att välja $\sigma$ finns i.

För att troget representera en Markov-matris måste $K$ normaliseras med motsvarande gradmatris $D$ :

$P=D^{-1}K.$

$P$ representerar nu en Markov-kedja. $P(x_{i},x_{j})$ är sannolikheten för övergång från $x_{i}$ till $x_{j}$ i ett steg. På liknande sätt ges sannolikheten för övergång från $x_{i}$ till $x_{j}$ i t tidssteg av $P^{t }(x_{i},x_{j})$ . Här $P^{t}$ matrisen $P$ multiplicerad med sig själv t gånger.

Markov-matrisen $P$ utgör en uppfattning om lokal geometri för datamängden X . Den största skillnaden mellan diffusionskartor och huvudkomponentanalys är att endast lokala särdrag av data beaktas i diffusionskartor i motsats till att ta korrelationer av hela datamängden.

$K$ definierar en slumpmässig vandring på datamängden vilket innebär att kärnan fångar en viss lokal geometri hos datamängden. Markov-kedjan definierar snabba och långsamma utbredningsriktningar genom kärnvärdena. När vandringen fortplantar sig framåt i tiden, aggregeras den lokala geometriinformationen på samma sätt som lokala övergångar (definierade av differentialekvationer) i det dynamiska systemet. Metaforen för diffusion härrör från definitionen av ett familjediffusionsavstånd $\{D_{t}\}_{t\in N}$

$D_{t}^{2}(x,y)=\|p_{t} (x,\cdot )-p_{t}(y,\cdot )\|^{2}$

För fast t definierar $D_{t}$ ett avstånd mellan två godtyckliga punkter i datamängden baserat på sökvägsanslutningen: värdet på $D_{t}(x, y)$ blir mindre ju fler vägar som ansluter x till y och vice versa. Eftersom kvantiteten $D_{t}(x,y)$ innebär en summa över alla banor med längden t, är $D_{t}$ mycket mer robust mot brus i data än geodetiska avstånd. $D_{t}$ tar hänsyn till all relation mellan punkterna x och y när avståndet beräknas och fungerar som en bättre föreställning om närhet än bara euklidiskt avstånd eller till och med geodesiskt avstånd.

Lokal flerdimensionell skalning

Lokal flerdimensionell skalning utför flerdimensionell skalning i lokala regioner och använder sedan konvex optimering för att passa ihop alla delar.

Icke-linjär PCA

Icke-linjär PCA (NLPCA) använder backpropagation för att träna en multi-layer perceptron (MLP) för att passa till ett grenrör. Till skillnad från vanlig MLP-träning, som bara uppdaterar vikterna, uppdaterar NLPCA både vikterna och ingångarna. Det vill säga att både vikter och indata behandlas som latenta värden. Efter träning är de latenta ingångarna en lågdimensionell representation av de observerade vektorerna, och MLP mappar från den lågdimensionella representationen till det högdimensionella observationsutrymmet.

Datadriven högdimensionell skalning

Datadriven högdimensionell skalning (DD-HDS) är nära relaterad till Sammons kartläggning och kurvlinjära komponentanalys förutom att (1) den samtidigt straffar falska grannskap och tårar genom att fokusera på små avstånd i både original- och utmatningsutrymmet, och att (2 ) den tar hänsyn till fenomenet koncentration av mått genom att anpassa viktningsfunktionen till avståndsfördelningen.

Skulptering av grenrör

Manifold Sculpting använder graderad optimering för att hitta en inbäddning. Liksom andra algoritmer, beräknar den de k -närmaste grannarna och försöker söka en inbäddning som bevarar relationer i lokala grannskap. Den skalar långsamt varians från högre dimensioner, samtidigt som den justerar punkter i lägre dimensioner för att bevara dessa relationer. Om skalningshastigheten är liten kan den hitta mycket exakta inbäddningar. Den har högre empirisk noggrannhet än andra algoritmer med flera problem. Den kan också användas för att förfina resultaten från andra mångfaldiga inlärningsalgoritmer. Det kämpar för att veckla ut vissa grenrör, dock om inte en mycket långsam skalningshastighet används. Den har ingen modell.

RankVisu

RankVisu är utformad för att bevara rankningen av grannskapet snarare än avståndet. RankVisu är särskilt användbart vid svåra uppgifter (när bevarandet av avstånd inte kan uppnås på ett tillfredsställande sätt). I själva verket är grannskapsgraden mindre informativ än avstånd (rang kan härledas från avstånd men avstånd kan inte härledas från rang) och dess bevarande är således lättare.

Topologiskt begränsad isometrisk inbäddning

Topologiskt begränsad isometrisk inbäddning (TCIE) är en algoritm baserad på approximering av geodetiska avstånd efter filtrering av geodesik som inte överensstämmer med den euklidiska metriken. Syftet till att korrigera de förvrängningar som orsakas när Isomap används för att kartlägga i sig icke-konvexa data, använder TCIE vikt minsta kvadraters MDS för att få en mer exakt mappning. TCIE-algoritmen detekterar först möjliga gränspunkter i datan, och under beräkningen av den geodetiska längden markerar inkonsekvent geodesik, för att få en liten vikt i den viktade spänningsmajorisering som följer.

Enhetlig grenrörsapproximation och projektion

Uniform manifold approximation and projection (UMAP) är en ickelinjär dimensionsreduktionsteknik. Visuellt liknar det t-SNE, men det förutsätter att data är likformigt fördelade på ett lokalt anslutet Riemann-grenrör och att Riemann-metriken är lokalt konstant eller ungefär lokalt konstant.

Metoder baserade på närhetsmatriser

En metod baserad på närhetsmatriser är en där data presenteras för algoritmen i form av en likhetsmatris eller en avståndsmatris . Dessa metoder faller alla under den bredare klassen av metrisk flerdimensionell skalning . Variationerna tenderar att vara skillnader i hur närhetsdata beräknas; till exempel isomap , lokalt linjära inbäddningar , maximal variansutveckling och Sammon-mappning (som i själva verket inte är en mappning) är exempel på metriska flerdimensionella skalningsmetoder.

Se även

• Flerfaldig hypotes
• Spektralt undergrenrör
• Takens sats
• Whitneys inbäddningssats
• Diskriminerande analys
• Elastisk karta
• Funktionsinlärning
• Växande självorganiserande karta (GSOM)
• Självorganiserande karta (SOM)

Vidare läsning

•   Murphy, Kevin P. (2022). "Mångfaldigt lärande" . Probabilistisk maskininlärning . MIT Press. s. 682–699. ISBN 978-0-262-04682-4 .

externa länkar

• Isomap
• Generativ topografisk kartläggning
• Mike Tippings avhandling
• Gaussisk process latent variabel modell
• Lokalt linjär inbäddning
• Relationsperspektivkarta
• Waffles är ett C++-bibliotek med öppen källkod som innehåller implementeringar av LLE, Manifold Sculpting och några andra mångfaldiga inlärningsalgoritmer.
• DD-HDS hemsida
• RankVisu hemsida
• Kort recension av Diffusion Maps
• Icke-linjär PCA av autoencoder neurala nätverk