Radikal axel

Den här artikeln handlar om den radikala axeln som används i geometri. För animationsstudion, se Radical Axis (studio) .

  Två cirklar, centrerade vid M ₁ , M ₂

  Radikal axel, med provpunkt P

  Tangentiala avstånd från båda cirklarna till P

Tangentlinjerna måste vara lika långa för varje punkt på den radikala axeln: $|PT_{1}|=|PT_{2}|.$ Om P , T ₁ , T ₂ ligger på en gemensam tangent, så är P mittpunkten av ${\overline {T_{1}T_{2}}}.$

I euklidisk geometri är den radikala axeln för två icke-koncentriska cirklar uppsättningen av punkter vars styrka med avseende på cirklarna är lika. Av denna anledning kallas den radikala axeln också kraftledningen eller potenshalveringslinjen för de två cirklarna. I detalj:

För två cirklar c ₁ , c ₂ med centrum M ₁ , M ₂ och radier r ₁ , r _{2 är} potenserna för en punkt P med avseende på cirklarna

$\Pi _{1}(P)=|PM_{1}|^{2}-r_{1}^{2},\qquad \Pi _{2}(P)=|PM_{2} |^{2}-r_{2}^{2}.$

Punkt P tillhör den radikala axeln, if

$\Pi _{1}(P)=\Pi _{2}(P).$

Om cirklarna har två punkter gemensamma är den radikala axeln cirklarnas gemensamma sekantlinje . Om punkt P är utanför cirklarna har P lika tangentiellt avstånd till båda cirklarna. Om radierna är lika, är den radikala axeln linjesegmentets halveringslinje för M ₁ , M ₂ . I vilket fall som helst är den radikala axeln en linje vinkelrät mot ${\overline {M_{1}M_{2}}}.$

På noteringar

Notationen radikal axel användes av den franske matematikern M. Chasles som yxradikal . JV Poncelet använde chorde ideale . J. Plücker introducerade termen Chordale . J. Steiner kallade den radikala axellinjen för lika makter ( tyska : Linie der gleichen Potenzen ) som ledde till kraftledning ( Potenzgerade ).

Egenskaper

Geometrisk form och dess position

Låt ${\displaystyle {\vec {x}},{\vec {m}}_{1},{\vec {m}}_{2}} vara$ positionsvektorerna av punkterna $P,M_{1},M_{2}$ . Då kan den definierande ekvationen för den radikala linjen skrivas som:

$({\vec {x}}-{\vec {m}}_{1})^{2}-r_{1}^{2}=({ \vec {x}}-{\vec {m}}_{2})^{2}-r_{2}^{2}\quad \leftrightarrow \quad 2{\vec {x}}\cdot ({ \vec {m}}_{2}-{\vec {m}}_{1})+{\vec {m}}_{1}^{2}-{\vec {m}}_{2 }^{2}+r_{2}^{2}-r_{1}^{2}=0$

Definition och beräkning av $d_{1},d_{2}$

Från den rätta ekvationen får man

• Radikalaxelns spetsmängd är verkligen en linje och är vinkelrät mot linjen genom cirkelns mittpunkter.

( ${\vec {m}}_{2}-{\vec {m}}_{1}$ är en normalvektor till den radikala axeln!)

Dividera ekvationen med ${\displaystyle 2|{\vec {m}}_{2}-{\vec {m}}_{1}|} ,$ man får den hessiska normalformen . Att infoga positionsvektorerna för centran ger centrans avstånd till den radikala axeln:

$d_{1}={\frac {d^{2}+{ r_{1}}^{2}-{r_{2}}^{2}}{2d}}\ ,\qquad d_{2}={\frac {d^{2}+{r_{2}} ^{2}-{r_{1}}^{2}}{2d}}$ ,

med $d=|M_{1}M_{2}|$ .

( $d_{i}$ kan vara negativ om $L$ inte är mellan $M_{1},M_{2}$ .)

Om cirklarna skär varandra i två punkter, går den radikala linjen genom de gemensamma punkterna. Om de bara rör vid varandra är den radikala linjen den gemensamma tangentlinjen.

Specialbefattningar

Radikal axel: variationer

• Den radikala axeln för två skärande cirklar är deras gemensamma sekantlinje.

Den radikala axeln för två rörande cirklar är deras gemensamma tangent.

Den radikala axeln för två icke- korsande cirklar är den gemensamma sekanten för två bekväma ekvikraftscirklar (se nedan).

Ortogonala cirklar

Beröringspunkterna för tangenterna genom $P$ ligger på den ortogonala cirkeln (grön)

• För en punkt $P$ utanför en cirkel $c_{i}$$S_{i},T_{i}$ de två tangentpunkterna ekvationen $|PS_{i}|^{2}=|PT_{i}|^{2}=\Pi _{i}(P)$${ \displaystyle S_{i},T_{i}}$ och ligger på cirkeln $c_{o}$ med mitten $P$ och radien ${\sqrt {\Pi _{i}(P)}}$ . Cirkel $c_{o}$ skär $c_{i}$ ortogonalt. Därför:

Om $P$ är en punkt på den radikala axeln, då de fyra punkterna $S_{1},T_{1},S_{2}, T_{2}$ ligger på cirkeln $c_{o}$ , som skär de givna cirklarna $c_{1},c_{2}$ ortogonalt .

• Den radikala axeln består av alla centra av cirklar , som skär de givna cirklarna ortogonalt.

System av ortogonala cirklar

Metoden som beskrivs i föregående avsnitt för konstruktion av en penna av cirklar, som skär två givna cirklar ortogonalt, kan utvidgas till konstruktionen av två ortogonalt skärande system av cirklar:

Låt $c_{1},c_{2}$ vara två från varandra liggande cirklar (som i föregående avsnitt), $M_{1} ,M_{2},r_{1},r_{2}$ deras mittpunkter och radier och $g_{12}$ deras radikalaxel. Nu kommer alla cirklar att bestämmas med mittpunkter på linje ${\displaystyle {\overline {M_{1}M_{2}}}} ,$ som tillsammans med $c_{1}$ linje $g_{12}$ som radikal axel också. Om $\gamma _{2}$ är en sådan cirkel, vars centrum har avståndet $\delta$ till mitten $M_{1}$ och radien $\ rho _{2}$ . Från resultatet i föregående avsnitt får man ekvationen

$d_{1}={\frac {\delta ^{2}+r_{1}^{2}-\rho _{2}^ {2}}{2\delta }}\quad$ , där $d_{1}>r_{1}$ är fixerade.

Med $\delta _{2}=\delta -d_{1}$ kan ekvationen skrivas om som:

$\delta _{2}^{2}=d_{1}^{2}-r_{1}^{2}+\rho _ {2}^{2}$ .

System av ortogonala cirklar: konstruktion

Om radien $\rho _{2}$ ges, från denna ekvation finner man avståndet $\delta _{2}$ till den (fasta) radikalaxeln för det nya centrumet. I diagrammet är färgen på de nya cirklarna lila. Varje grön cirkel (se diagram) har sitt centrum på den radikala axeln och skär cirklarna $c_{1},c_{2}$ ortogonalt och därmed alla nya cirklar (lila) också. Om du väljer den (röda) radikalaxeln som y-axel och linjen ${\overline {M_{1}M_{2}}}$ som x-axel, har de två cirklarnas ekvationer:

lila: $\ \ \ (x-\delta _{2})^{2}+y^{2} =\delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}$

grön: $\ x^{2}+(y-y_{g})^{2}=y_{g}^{2}+d_{1}^{2}-r_{1}^{2}\ .$

( $\;(0,y_{g})$ är mitten av en grön cirkel.)

Egenskaper: a) Alla två gröna cirklar skär varandra på x-axeln i punkterna $d_{1}^{2}-r_{1}^{2}}},0{\big )}} ,$${\displaystyle P_{1/2}={\big (}\pm {\sqrt$ { polerna för det ortogonala systemet av cirklar. Det betyder att x-axeln är den radikala linjen för de gröna cirklarna. b) De lila cirklarna har inga punkter gemensamma. Men om man betraktar det reella planet som en del av det komplexa planet, så skär två lila cirklar varandra på y-axeln (deras gemensamma radikalaxel) vid punkterna $Q_{1/2}={\big (}0,\pm i{\sqrt {d_{1}^{2}-r_{1}^{2}}}{\big )}$ .

Paraboliskt ortogonalt system

Koaxala cirklar: typer

Speciella fall: a) I fallet $d_{1}=r_{1}$ berör de gröna cirklarna varandra vid utgångspunkten med x-axeln som gemensam tangent och de lila cirklarna har y-axeln som gemensam tangent. Ett sådant system av cirklar kallas koaxala paraboliska cirklar (se nedan). b) Krympa $c_{1}$ till mitten $M_{1}$ , dvs. e. $r_{1}=0$ , ekvationerna förvandlas till en enklare form och man får $M_{1}=P_{1}$ .

Slutsats: a) För alla verkliga $w$ pennan av cirklar

$\;c(\xi ):\;(x-\xi )^{2}+y^{2} -\xi ^{2}-w=0\ :$

har egenskapen: Y-axeln är den radikala axeln för $c(\xi _{1}) ,c(\xi _{2})$ .

I fallet med ${\displaystyle w>0} skär$ cirklarna $c(\xi _{1}),c(\xi _{2})$ vid poäng $P_{1/2}=(0,\pm {\sqrt {w}})$ .

I fallet med $w<0$ har de inga punkter gemensamma.

I fallet med $w=0$ pekar de vid $(0,0)$ och y-axeln är deras gemensamma tangent.

b) För alla riktiga $w$ de två cirklarna

$c_{1}(\xi ):\;(x-\xi )^{2}+y^{ 2}-\xi ^{2}-w=0\ ,$

$​​{\displaystyle c_{2}(\eta ):\ ;x^{2}+(y-\eta )^{2}-\eta ^{2}+w=0\ }$

bildar ett system av ortogonala cirklar . Det betyder: två valfria cirklar $c_{1}(\xi ),c_{2}(\eta )$ skär ortogonalt.

c) Från ekvationerna i b) får man en koordinatfri representation:

Ortogonalt system av cirklar till givna poler $P_{1},P_{2}$

För de givna punkterna $P_{1},P_{2}$ , deras mittpunkt $O$ och deras linjesegmentshalveringslinje $g_{12}$ de två ekvationerna

$|XM|^{2}=|OM|^{2}-|OP_{1}|^{2}\ ,$

$|XN|^{2}=|ON|^{2}+|OP_{1}|^{2}=|NP_{1}|^{2}$

med $M$ på ${\overline {P_{1}P_{2}}}$ , men inte mellan $P_{1},P_{2}$ och ${\ displaystyle N}$ på $g_{12}$

beskriver det ortogonala systemet av cirklar som unikt bestäms av $P_{1},P_{2}$ som är systemets poler.

För $P_{1}=P_{2}=O$ måste man föreskriva axlarna $a_{1},a_{2}$ för systemet också. Systemet är paraboliskt :

$|XM|^{2}=|OM|^{2}\ ,\quad |XN|^{2}=|ON|^{2}$

med $M$ på ${ \displaystyle a_{1}}$ och $N$ på $a_{2}$ .

Rätriktad och kompasskonstruktion:

Ortogonalt system av cirklar: rätkant och kompasskonstruktion

Ett system av ortogonala cirklar bestäms unikt av dess poler $P_{1},P_{2}$ :

1. Axlarna (radikala axlarna) är linjerna ${\overline {P_{1}P_{2}}}$ och linjesegmentets bisektris $g_{12}$ för polerna .
2. Cirklarna (gröna i diagrammet) till $P_{1},P_{2}$ har sina mittpunkter på $g_{12}$ . De kan enkelt ritas. För en punkt $N$ är radien $\;r_{N}=|NP_{1}|\;$ .
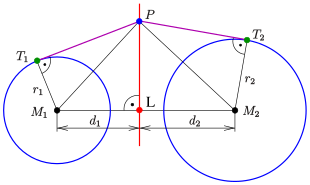
3. För att rita en cirkel av den andra pennan (i diagram blå) med mitten $M$ på ${\overline {P_{1}P_{2}}}$ bestämmer man radien $r_{M}$ med tillämpning av Pythagoras sats : $\;r_{M}^{2}=|OM|^{2}-|OP_{1}|^{2}\;$ (se diagram).

I fallet $P_{1}=P_{2}$ måste axlarna väljas ytterligare. Systemet är paraboliskt och kan enkelt ritas.

Koaxala cirklar

Definition och egenskaper:

Låt $c_{1},c_{2}$ vara två cirklar och $\Pi _{1},\Pi _{2}$ deras potensfunktioner. Sedan för alla $\lambda \neq 1$

• $\Pi _{1}(x,y)-\lambda \Pi _{2}(x,y)=0$

är ekvationen för en cirkel $c(\lambda )$ (se nedan). Ett sådant system av cirklar kallas koaxala cirklar som genereras av cirklarna $c_{1},c_{2}$ . (I fallet med $\lambda =1$ beskriver ekvationen den radikala axeln för $c_{1},c_{2}$ .)

Potensfunktionen för $c(\lambda )$ är

$\ \Pi (\lambda ,x,y)={\frac {\Pi _ {1}(x,y)-\lambda \Pi _{2}(x,y)}{1-\lambda }}$ .

Den normerade ekvationen (koefficienterna för $x^{2},y^{2}$ är $1$ ) av $c(\lambda )$ är $\ \Pi (\lambda ,x,y)=0$ .

En enkel beräkning visar:

• $c(\lambda ),c(\mu ),\ \lambda \neq \mu \ ,$ har samma radikalaxel som $c_{1},c_{2}$ .

Genom att tillåta $\lambda$ att röra sig till oändligheten inser man att $c_{1},c_{2}$ är medlemmar av systemet av koaxala cirklar: $c_{1}=c(0),\;c_{2}=c(\infty )$ .

(E): Om $c_{1},c_{2}$ skär varandra vid två punkter $P_{1},P_{2}$ , valfri cirkel $c(\lambda )$ innehåller $P_{1},P_{2}$ också, och linje ${\overline {P_{1 }P_{2}}}$ är deras gemensamma radikalaxel. Ett sådant system kallas elliptiskt . (P): Om $c_{1},c_{2}$ tangerar $P$ , är vilken cirkel som helst tangent till c 1 $displaystyle c_{1} ,c_{2}}$ vid punkt $P$ också. Den gemensamma tangenten är deras gemensamma radikalaxel. Ett sådant system kallas paraboliskt . (H): Om ${\displaystyle c_{1},c_{2}} inte$ har någon poäng gemensamt , så är det också något par i systemet. Radikalaxeln för valfritt par av cirklar är radikalaxeln för $c_{1},c_{2}$ . Systemet kallas hyperboliskt .

I detalj:

Att införa koordinater så att

$c_{1}:(x-d_{1})^{2}+y^{2}=r_{1}^{ 2}$

$c_{2}:(x-d_{2})^{2}+y ^{2}=d_{2}^{2}+r_{1}^{2}-d_{1}^{2}$ ,

då är y-axeln deras radikala axel (se ovan).

Att beräkna potensfunktionen $\Pi (\lambda ,x,y)$ ger den normerade cirkelekvationen:

$c(\lambda ):\ x^{2}+y^{2}-2{\tfrac {d_{1}-\lambda d_{2}}{1-\lambda }}\;x+ d_{1}^{2}-r_{1}^{2}=0\ .$

Komplettera kvadraten och substitutionen $\delta _{2}={\tfrac {d_{1}-\lambda d_{2}}{1-\lambda } }$ (x-koordinat för mitten) ger den centrerade formen av ekvationen

$c(\lambda ):\ (x-\delta _{2})^{2 }+y^{2}=\delta _{2}^{2}+r_{1}^{2}-d_{1}^{2}$ .

I fallet $r_{1}>d_{1}$ cirklarna $c_{1},c_{2},c(\lambda )$ har de två punkterna

$P_{1}={\big (}0,{\sqrt {r_{1 }^{2}-d_{1}^{2}}}{\big )},\quad P_{2}={\big (}0,-{\sqrt {r_{1}^{2}- d_{1}^{2}}}{\big )}$

gemensamt och systemet med koaxala cirklar är elliptiskt .

I fallet med $r_{1}=d_{1}$ cirklarna $c_{1},c_{2},c(\lambda )$ har punkten $P_{0}=(0,0)$ gemensam och systemet är paraboliskt .

I fallet med $r_{1}<d_{1}$ cirklarna $c_{1},c_{2},c(\lambda )$ har ingen mening gemensamt och systemet är hyperboliskt .

Alternativa ekvationer: 1) I den definierande ekvationen för ett koaxalt system av cirklar kan även multiplar av potensfunktionerna användas. 2) Ekvationen för en av cirklarna kan ersättas med ekvationen för den önskade radikalaxeln. Radikalaxeln kan ses som en cirkel med en oändligt stor radie. Till exempel:

$(x-x_{1})^{2}+y^{2}-r_{1 }^{2}\ -\ \lambda \;2(x-x_{2})\ =0\ \Leftrightarrow$

$(x-(x_{1}+\lambda ))^{2}+y^{2}=(x_{1}+\lambda )^ {2}+r_{1}^{2}-x_{1}^{2}-2\lambda x_{2}$ ,

beskriver alla cirklar, som med den första cirkeln har linjen $x=x_{2}$ som radikalaxel. 3) För att uttrycka lika status för de två cirklarna används ofta följande form:

$\mu \Pi _{1}(x,y)+\nu \Pi _{2}(x,y)=0\;.$

är representationen av en cirkel med parametrarna $\mu ,\nu$ inte unik .

Tillämpningar: a) Cirkelinversioner och Möbiustransformationer bevarar vinklar och generaliserade cirklar . Därför spelar ortogonala system av cirklar en viktig roll vid undersökningar av dessa kartläggningar. b) I elektromagnetism uppträder koaxala cirklar som fältlinjer .

Radikalt centrum av tre cirklar, konstruktion av den radikala axeln

Radikalt centrum av tre cirklar Den gröna cirkeln skär de tre cirklarna ortogonalt.

• För tre cirklar ${\displaystyle c_{1},c_{2},c_{3}} ,$ varav inte två är koncentriska, finns det tre radikala axlar $g_{12},g_{23},g_{31}$ . Om cirkelcentrum inte ligger på en linje, skär de radikala axlarna i en gemensam punkt $R$ , de tre cirklarnas radikala centrum . Den ortogonala cirkeln centrerad runt $R$ av två cirklar är också ortogonal mot den tredje cirkeln ( radikal cirkel) .

Bevis: den radikala axeln $g_{ik}$ innehåller alla punkter som har lika tangentiellt avstånd till cirklarna $c_{i},c_{k}$ . Skärningspunkten $R$ för $g_{12}$ och $g_{23}$ har samma tangentiella avstånd till alla tre cirklarna. Därför $R$ också en punkt på den radikala axeln ${\displaystyle g_{31}} .$

Denna egenskap tillåter en att konstruera den radikala axeln för två icke-korsande cirklar $c_{1},c_{2}$ med mittpunkter ${\displaystyle M_{1},M_{$ : Rita en tredje cirkel $c_{3}$ med mitten inte i linje med de givna mittpunkterna som skär $c_{1},c_{2}$ . De radikala axlarna $g_{13},g_{23}$ kan ritas. Deras skärningspunkt är det radikala mitten $R$ av de tre cirklarna och ligger på $g_{12}$ . Linjen genom $R$ som är vinkelrät mot ${\overline {M_{1}M_{2}}}$ är den radikala axeln $g_{12}$ .

Ytterligare konstruktionsmetod:

Konstruktion av den radikala axeln med cirklar $c'_{1},c'_{2}$ med lika stor styrka. Det är $\Pi _{1}(P_{1})=\Pi _{2}(P_{2})$ .

Alla punkter som har samma makt till en given cirkel $c$ ligger på en cirkel koncentrisk med $c$ . Låt oss kalla det en ekvikraftscirkel . Denna egenskap kan användas för en ytterligare konstruktionsmetod för två cirklars radikala axel:

För två icke-korsande cirklar $c_{1},c_{2}$ kan det ritas två ekvipotenscirklar $c'_{1},c' _{2}$ , som har samma makt med avseende på $c_{1},c_{2}$ (se diagram). I detalj: $\Pi _{1}(P_{1})=\Pi _{2}(P_{2})$ . Om styrkan är tillräckligt stor har cirklarna $c'_{1},c'_{2}$ två punkter gemensamma, som ligger på den radikala axeln $g_{12}$ .

Relation till bipolära koordinater

I allmänhet kan två osammanhängande, icke-koncentriska cirklar ställas i linje med cirklarna i ett system av bipolära koordinater . I så fall är den radikala axeln helt enkelt $y$ -axeln för detta koordinatsystem. Varje cirkel på axeln som passerar genom koordinatsystemets två härdar skär de två cirklarna ortogonalt. En maximal samling cirklar, som alla har centra på en given linje och alla par har samma radikalaxel, är känd som en blyertspenna med koaxala cirklar .

Radikalt centrum i trilinjära koordinater

Om cirklarna representeras i trilinjära koordinater på vanligt sätt, så ges deras radikala centrum lämpligen som en viss determinant. Närmare bestämt, låt X = x : y : z beteckna en variabel punkt i planet för en triangel ABC med sidolängder a = | BC |, b = | CA |, c = | AB |, och representerar cirklarna enligt följande:

( dx + ey + fz )( ax + by + cz ) + g ( ayz + bzx + cxy ) = 0

( hx + iy + jz )( ax + by + cz ) + k ( ayz + bzx + cxy ) = 0

( lx + my + nz )( ax + by + cz ) + p ( ayz + bzx + cxy ) = 0

Då är det radikala mitten poängen

$\det {\begin{bmatrix}g&k&p\\e&i&m\\f&j&n\end{bmatrix}}:\det {\begin{bmatrix}g&k&p\\f&j&n\\d&h&l\end{bmatrix}}:\det { \begin{bmatrix}g&k&p\\d&h&l\\e&i&m\end{bmatrix}}.$

Radikalt plan och hyperplan

Radikalplanet för två icke-koncentriska sfärer i tre dimensioner definieras på liknande sätt: det är platsen för punkter från vilka tangenterna till de två sfärerna har samma längd . Att detta lokus är ett plan följer av rotation i den tredje dimensionen av att den radikala axeln är en rät linje.

Samma definition kan tillämpas på hypersfärer i det euklidiska rummet av vilken dimension som helst, vilket ger det radikala hyperplanet för två icke-koncentriska hypersfärer.

Anteckningar

•   RA Johnson (1960). Advanced Euclidean Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle (omtryck av 1929 års upplaga av Houghton Mifflin red.). New York: Dover Publications. s. 31 –43. ISBN 978-0-486-46237-0 .

Vidare läsning

•   C. Stanley Ogilvy (1990). Utflykter i geometri . Dover. s. 17–23 . ISBN 0-486-26530-7 .
•   HSM Coxeter , SL Greitzer (1967). Geometri Revisited . Washington, DC : Mathematical Association of America . s. 31 –36, 160–161. ISBN 978-0-88385-619-2 .
• Clark Kimberling, "Triangle Centers and Central Triangles," Congressus Numerantium 129 (1998) i–xxv, 1–295.

externa länkar

• Weisstein, Eric W. "Radikal linje" . MathWorld .
• Weisstein, Eric W. "Chordal theorem" . MathWorld .
• Animation på Cut-the-knot