Fältlinje

Den här artikeln handlar om den moderna användningen av "fältlinjer" som ett sätt att avbilda elektromagnetiska och andra vektorfält. För vilken roll dessa linjer har i elektromagnetismens tidiga historia och filosofi, se Line of force .

Fältlinjer som visar det elektriska fältet som skapas av en positiv laddning (vänster), negativ laddning (mitten) och oladdat föremål (höger).

En fältlinje är ett grafiskt visuellt hjälpmedel för att visualisera vektorfält . Den består av en tänkt integralkurva som tangerar fältvektorn vid varje punkt längs dess längd . Ett diagram som visar en representativ uppsättning av närliggande fältlinjer är ett vanligt sätt att avbilda ett vektorfält i vetenskaplig och matematisk litteratur; detta kallas ett fältlinjediagram . De används för att visa elektriska fält , magnetiska fält och gravitationsfält bland många andra typer. Inom vätskemekanik kallas fältlinjer som visar hastighetsfältet för ett vätskeflöde strömlinjer .

Definition och beskrivning

Figuren till vänster visar de elektriska fältlinjerna för två lika positiva laddningar. Figuren till höger visar de elektriska fältlinjerna för två lika laddningar med motsatt tecken.

Ett vektorfält definierar en riktning och storlek vid varje punkt i rymden. En fältlinje är en integralkurva för det vektorfältet och kan konstrueras genom att börja vid en punkt och spåra en linje genom rymden som följer vektorfältets riktning, genom att göra fältlinjen att tangera fältvektorn vid varje punkt. En fältlinje visas vanligtvis som ett riktat linjesegment, med en pilspets som anger vektorfältets riktning. För tvådimensionella fält är fältlinjerna plana kurvor; eftersom en planritning av en 3-dimensionell uppsättning fältlinjer kan vara visuellt förvirrande är de flesta fältlinjediagram av denna typ. Eftersom vektorfältet vid varje punkt där det är icke-noll och ändligt har en unik riktning, kan fältlinjer aldrig skära varandra, så det finns exakt en fältlinje som passerar genom varje punkt där vektorfältet är icke-noll och ändligt. Punkter där fältet är noll eller oändligt har ingen fältlinje genom dem, eftersom riktning inte kan definieras där, men kan vara ändpunkterna för fältlinjer.

Eftersom det finns ett oändligt antal punkter i vilken region som helst, kan ett oändligt antal fältlinjer ritas; men endast ett begränsat antal kan visas på ett fältlinjediagram. Vilka fältlinjer som visas är därför ett val som gjorts av personen eller datorprogrammet som ritar diagrammet, och ett enda vektorfält kan avbildas av olika uppsättningar av fältlinjer. Ett fältlinjediagram är nödvändigtvis en ofullständig beskrivning av ett vektorfält, eftersom det inte ger någon information om fältet mellan de ritade fältlinjerna, och valet av hur många och vilka linjer som ska visas avgör hur mycket användbar information diagrammet ger.

En enskild fältlinje visar vektorfältets riktning men inte storleken . För att också avbilda storlek , ritas ofta fältlinjediagram så att varje linje representerar samma mängd flöde . Då är tätheten av fältlinjer (antal fältlinjer per enhet vinkelrät area) vid valfri plats proportionell mot storleken på vektorfältet vid den punkten. Områden där närliggande fältlinjer konvergerar (kommer närmare varandra) indikerar att fältet blir starkare i den riktningen.

I vektorfält som har divergens som inte är noll börjar fältlinjerna på punkter med positiv divergens ( källor ) och slutar på punkter med negativ divergens ( sjunker ), eller sträcker sig till oändlighet. Till exempel elektriska fältlinjer på positiva laddningar och slutar på negativa laddningar. I fält som är divergenslösa ( solenoidala ), såsom magnetiska fält , har fältlinjer inga ändpunkter; de är antingen slutna slingor eller oändliga.

Inom fysiken är ritningar av fältlinjer främst användbara i fall där källorna och sänkorna, om några, har en fysisk betydelse, i motsats till t.ex. fallet med ett kraftfält av en radiell överton . Till exempel säger Gauss lag att ett elektriskt fält har källor vid positiva laddningar , sjunker vid negativa laddningar och inte någon annanstans, så elektriska fältlinjer börjar med positiva laddningar och slutar med negativa laddningar. Ett gravitationsfält har inga källor, det har sjunkit i massor, och det har inte heller någon annanstans, gravitationsfältslinjer kommer från oändligheten och slutar vid massor. Ett magnetfält har inga källor eller sjunker ( Gauss' lag för magnetism ), så dess fältlinjer har ingen början eller slut: de kan bara bilda slutna slingor, sträcka sig till oändlighet i båda riktningarna eller fortsätta i det oändliga utan att någonsin korsa sig själv. Men som nämnts ovan kan en speciell situation uppstå runt punkter där fältet är noll (som inte kan skäras av fältlinjer, eftersom deras riktning inte skulle definieras) och den samtidiga början och slutet av fältlinjer äger rum. Denna situation inträffar till exempel i mitten mellan två identiska positiva elektriska punktladdningar. Där försvinner fältet och linjerna som kommer axiellt från laddningarna slutar. Samtidigt, i det tvärgående planet som passerar genom mittpunkten, divergerar ett oändligt antal fältlinjer radiellt. Den samtidiga närvaron av linjerna som slutar och börjar bevarar den divergensfria karaktären hos fältet i punkten.

Observera att för denna typ av ritning, där fältlinjedensiteten är avsedd att vara proportionell mot fältets storlek, är det viktigt att representera alla tre dimensionerna. Tänk till exempel på det elektriska fältet som härrör från en enda, isolerad punktladdning . De elektriska fältlinjerna i detta fall är raka linjer som utgår från laddningen likformigt i alla riktningar i det tredimensionella rummet. Detta betyder att deras densitet är proportionell mot ${\displaystyle 1/r^{2}} ,$ det korrekta resultatet överensstämmer med Coulombs lag för detta fall. Men om de elektriska fältlinjerna för denna uppsättning bara ritades på ett tvådimensionellt plan, skulle deras tvådimensionella densitet vara proportionell mot $1/r$ , ett felaktigt resultat för denna situation.

Konstruktion

Konstruktion av en fältlinje

Givet ett vektorfält $\mathbf {F} (\mathbf {x} )$ och en startpunkt $\mathbf {x} _{\text{0}}$ kan en fältlinje konstrueras iterativt genom att hitta fältvektorn vid den punkten $\mathbf {F} (\mathbf {x} _{\text{0}})$ . Enhetstangensvektorn $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ den punkten är: ) . Genom att flytta en kort sträcka $ds$ längs fältriktningen kan en ny punkt på linjen hittas

$$\mathbf {x} _{\text{1}}=\mathbf {x} _{\text{0}}+{\mathbf {F} (\mathbf {x} _{\text{ 0}}) \over |\mathbf {F} (\mathbf {x} _{\text{0}})|}ds$$

hittas fältet vid den punkten ${\displaystyle \mathbf {F} (\mathbf {x} _{\text{1}})} och flyttar sig ytterligare ett avstånd$$ds$ in den riktningen hittas nästa punkt $\mathbf {F} (\mathbf {x} _{\text{2}})$ på fältlinjen. Vid varje punkt $\mathbf {x} _{\text{i}}$ kan nästa punkt hittas av

$$\mathbf {x} _{\text{i+1}}=\mathbf {x} _{\text{i}}+{\mathbf {F} (\mathbf {x} _{\ text{i}}) \over |\mathbf {F} (\mathbf {x} _{\text{i}})|}ds$$

Genom att upprepa detta och koppla ihop punkterna kan fältlinjen förlängas så långt som önskas. Detta är bara en approximation av den faktiska fältlinjen, eftersom varje rakt segment faktiskt inte tangerar fältet längs dess längd, bara vid dess startpunkt. Men genom att använda ett tillräckligt litet värde för ${\displaystyle ds} ,$ och ta ett större antal kortare steg, kan fältlinjen approximeras så nära som önskas. Fältlinjen kan förlängas i motsatt riktning från $\mathbf {x} _{\text{0}}$ genom att ta varje steg i motsatt riktning genom att använda ett negativt steg $-ds$ .

Exempel

Olika sätt att avbilda en magnets fält.

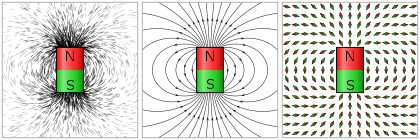
Om vektorfältet beskriver ett hastighetsfält , så följer fältlinjerna strömlinjer i flödet. Det kanske mest välbekanta exemplet på ett vektorfält som beskrivs av fältlinjer är magnetfältet, som ofta avbildas med fältlinjer som utgår från en magnet .

Divergens och krullning

Fältlinjer kan användas för att spåra bekanta storheter från vektorkalkyl :

• Divergens kan lätt ses genom fältlinjer, förutsatt att linjerna är ritade så att tätheten av fältlinjer är proportionell mot fältets storlek (se ovan). I detta fall kan divergensen ses som början och slutet av fältlinjer. Om vektorfältet är resultanten av radiella omvända kvadratiska lagfält med avseende på en eller flera källor så motsvarar detta det faktum att divergensen för ett sådant fält är noll utanför källorna. I ett solenoidalt vektorfält (dvs ett vektorfält där divergensen är noll överallt), varken börjar eller slutar fältlinjerna; de bildar antingen slutna slingor eller går till oändlighet i båda riktningarna. Om ett vektorfält har positiv divergens i något område kommer det att finnas fältlinjer som börjar från punkter i det området. Om ett vektorfält har negativ divergens i något område kommer det att finnas fältlinjer som slutar vid punkter i det området.
• Kelvin -Stokes-satsen visar att fältlinjer i ett vektorfält med noll curl (dvs ett konservativt vektorfält , t.ex. ett gravitationsfält eller ett elektrostatiskt fält ) inte kan vara slutna slingor. Med andra ord, curl är alltid närvarande när en fältlinje bildar en sluten slinga. Det kan förekomma i andra situationer också, såsom en spiralform av fältlinjer.

Fysisk betydelse

När de tappas slumpmässigt (som med shakern här), ordnar sig järnspån så att de ungefär avbildar några magnetfältslinjer. Magnetfältet skapas av en permanent magnet under glasytan.

Medan fältlinjer är en "bara" matematisk konstruktion, får de under vissa omständigheter fysisk betydelse. Inom vätskemekanik representerar hastighetsfältlinjerna ( strömlinjerna ) i stadigt flöde vätskepartiklarnas vägar. I samband med plasmafysik interagerar elektroner eller joner som råkar vara på samma fältlinje starkt, medan partiklar på olika fältlinjer i allmänhet inte interagerar . Detta är samma beteende som partiklarna i järnspån uppvisar i ett magnetfält.

Järnspån på bilden verkar vara i linje med diskreta fältlinjer, men situationen är mer komplex. Det är lätt att visualisera som en tvåstegsprocess: för det första sprids filningarna jämnt över magnetfältet men alla i linje i fältets riktning. Sedan, baserat på skalan och de ferromagnetiska egenskaperna hos filningarna, dämpar de fältet åt vardera sidan, vilket skapar de uppenbara utrymmena mellan linjerna som vi ser. Naturligtvis sker de två stadierna som beskrivs här samtidigt tills en jämvikt uppnås. Eftersom filningarnas inneboende magnetism modifierar fältet, är linjerna som visas av filningarna endast en approximation av fältlinjerna för det ursprungliga magnetfältet. Magnetiska fält är kontinuerliga och har inga diskreta linjer.

Se även

• Kraftfält (fysik)
• Fältlinjer av Julia uppsättningar
• Extern stråle — fältlinjer för Douady–Hubbard potential för Mandelbrot-uppsättningar eller ifyllda Julia-uppsättningar
• Kraftlinje
• Vektor fält
• Linjeintegral faltning

Vidare läsning

•   Griffiths, David J. (1998). Introduktion till elektrodynamik (3:e uppl.) . Prentice Hall. s. 65–67 och 232 . ISBN 978-0-13-805326-0 .

externa länkar

• Interaktiv Java-applet som visar de elektriska fältlinjerna för utvalda laddningspar Arkiverad 2011-08-13 på Wayback Machine av Wolfgang Bauer
• "Visualisering av fält och divergens och krullning" kursanteckningar från en kurs vid Massachusetts Institute of Technology.