Numerisk modellering (geologi)

Simulering av seismisk vågutbredning i global skala med hjälp av superdator för att lösa vågekvationer

Inom geologi är numerisk modellering en allmänt tillämpad teknik för att tackla komplexa geologiska problem genom beräkningssimulering av geologiska scenarier .

Numerisk modellering använder matematiska modeller för att beskriva de fysiska förhållandena för geologiska scenarier med hjälp av siffror och ekvationer. Ändå är vissa av deras ekvationer svåra att lösa direkt, till exempel partiella differentialekvationer . Med numeriska modeller kan geologer använda metoder, såsom finita differensmetoder , för att approximera lösningarna av dessa ekvationer. Numeriska experiment kan sedan utföras i dessa modeller, vilket ger de resultat som kan tolkas i samband med geologisk process. Både kvalitativ och kvantitativ förståelse för en mängd olika geologiska processer kan utvecklas via dessa experiment.

Numerisk modellering har använts för att hjälpa till i studiet av bergmekanik , termisk historia av stenar, rörelser av tektoniska plattor och jordens mantel. Vätskeflöde simuleras med numeriska metoder, och detta visar hur grundvatten rör sig, eller hur rörelser av den smälta yttre kärnan ger det geomagnetiska fältet.

Historia

Före utvecklingen av numerisk modellering var analog modellering , som simulerar naturen med reducerade skalor i massa, längd och tid, ett av de viktigaste sätten att ta itu med geologiska problem, till exempel att modellera bildandet av tryckbälten . Enkla analytiska eller semianalytiska matematiska modeller användes också för att hantera relativt enkla geologiska problem kvantitativt.

I slutet av 1960-talet till 1970-talet, efter utvecklingen av finita elementmetoder för att lösa kontinuummekaniska problem för civilingenjör , anpassades numeriska metoder för att modellera komplexa geologiska fenomen, till exempel vikning och mantelkonvektion . Med framsteg inom datorteknik har noggrannheten hos numeriska modeller förbättrats. Numerisk modellering har blivit ett viktigt verktyg för att tackla geologiska problem, särskilt för de delar av jorden som är svåra att observera direkt, såsom manteln och kärnan . Ändå är analog modellering fortfarande användbar för att modellera geologiska scenarier som är svåra att fånga i numeriska modeller, och kombinationen av analog och numerisk modellering kan vara användbar för att förbättra förståelsen av jordens processer.

Komponenter

Steg i numerisk modellering. Det första steget i numerisk modellering är att fånga det faktiska geologiska scenariot kvantitativt. Till exempel, i mantelkonvektionsmodellering används värmeekvationer för att beskriva värmeenergin som cirkulerar i systemet medan Navier–Stokes ekvationer beskriver flödet av viskös vätska (mantelberget). För det andra, eftersom dessa ekvationer är svåra att lösa, väljs diskretisering och numeriska metoder för att göra en approximation till de styrande ekvationerna. Sedan kan algoritmer i datorn beräkna de ungefärliga lösningarna. Slutligen kan tolkningen göras utifrån dessa lösningar. Till exempel, i mantelkonvektionsmodellering kan mantelflödet först visualiseras. Sedan kan förhållandet mellan flödesmönstren och ingångsparametrarna slutföras.

En allmän numerisk modellstudie består vanligtvis av följande komponenter:

Matematisk modell är en förenklad beskrivning av det geologiska problemet, såsom ekvationer och randvillkor. Dessa styrande ekvationer i modellen är ofta partiella differentialekvationer som är svåra att lösa direkt eftersom det handlar om derivatan av funktionen , till exempel vågekvationen .
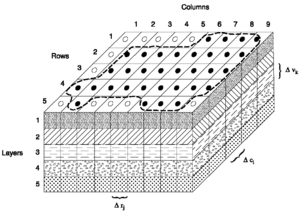
Diskretiseringsmetoder och numeriska metoder omvandlar de styrande ekvationerna i de matematiska modellerna till diskreta ekvationer. Dessa diskreta ekvationer kan approximera lösningen av de styrande ekvationerna. Vanliga metoder inkluderar den finita elementet , finita skillnaden eller finita volymmetoden som delar upp föremålet av intresse i mindre bitar (element) med nät. Dessa diskreta ekvationer kan sedan lösas i varje element numeriskt. Metoden med diskreta element använder ett annat tillvägagångssätt, denna metod återmonterar föremålet av intresse från många små partiklar. Enkla styrande ekvationer tillämpas sedan på interaktionerna mellan partiklar.
Algoritmer är datorprogram som beräknar lösningen med hjälp av idén om ovanstående numeriska metoder.
Tolkningar görs utifrån de lösningar som ges av de numeriska modellerna.

Egenskaper

En bra numerisk modell har vanligtvis några av följande egenskaper:

Konsekvent : Numeriska modeller delar ofta in objektet i mindre element. Om modellen är konsekvent är resultatet av den numeriska modellen nästan detsamma som vad den matematiska modellen förutsäger när elementstorleken är nästan noll. Med andra ord tenderar felet mellan de diskreta ekvationerna som används i den numeriska modellen och de styrande ekvationerna i den matematiska modellen att bli noll när maskens utrymme (storleken på elementet) blir nära noll.
Stabil : I en stabil numerisk modell förstärks inte felet under beräkningen av de numeriska metoderna. Felet i en instabil modell kommer att staplas snabbt och leda till ett felaktigt resultat. En stabil och konsekvent numerisk modell har samma effekt som den exakta lösningen i den matematiska modellen när avståndet mellan maskorna (elementets storlek) är extremt litet.
Konvergerande : Utdata från den numeriska modellen är närmare den faktiska lösningen av de styrande ekvationerna i de matematiska modellerna när avståndet mellan maskorna (storleken på elementet) minskar, vilket vanligtvis kontrolleras genom att utföra numeriska experiment.
Konserverad : De fysiska storheterna i modellerna, såsom massa och momentum, bevaras. Eftersom ekvationerna i de matematiska modellerna vanligtvis är härledda från olika bevarandelagar bör modellresultatet inte bryta mot dessa premisser.
Begränsad : Lösningen som ges av den numeriska modellen har rimliga fysiska gränser med avseende på de matematiska modellerna, till exempel bör massa och volym vara positiva.
Exakt : Lösningen som ges av de numeriska modellerna är nära den verkliga lösningen som förutspås av den matematiska modellen.

Beräkning

Följande är några nyckelaspekter av idéer för att utveckla numeriska modeller inom geologi. Först bör sättet att beskriva objektet och rörelsen bestämmas ( kinematisk beskrivning). Sedan skrivs styrande ekvationer som beskriver de geologiska problemen, till exempel värmeekvationerna värmeflödet i ett system. Eftersom vissa av dessa ekvationer inte kan lösas direkt, används numeriska metoder för att approximera lösningen av de styrande ekvationerna.

Kinematiska beskrivningar

I numeriska modeller och matematiska modeller finns det två olika tillvägagångssätt för att beskriva materiens rörelse: Eulerian och Lagrangian . Inom geologi används båda tillvägagångssätten vanligtvis för att modellera vätskeflöde som mantelkonvektion, där ett Eulerian rutnät används för beräkning och Lagrangian markörer används för att visualisera rörelsen. På senare tid har det funnits modeller som försöker beskriva olika delar med hjälp av olika tillvägagångssätt för att kombinera fördelarna med dessa två tillvägagångssätt. Detta kombinerade tillvägagångssätt kallas det godtyckliga Lagrangian-Eulerian tillvägagångssättet .

Eulerian

Eulerian-metoden beaktar förändringarna av de fysiska storheterna, såsom massa och hastighet, på en fast plats med tiden. Det liknar att titta på hur flodvatten rinner förbi en bro. Matematiskt kan de fysiska storheterna uttryckas som en funktion av plats och tid. Detta tillvägagångssätt är användbart för flytande och homogena (enhetliga) material som inte har någon naturlig gräns.

Lagrangian

Det lagrangska tillvägagångssättet, å andra sidan, överväger förändringen av fysiska storheter, såsom volymen, av fasta element av materia över tiden. Det liknar att titta på en viss samling vattenmolekyler när de rinner nedströms i en flod. Med den lagrangiska metoden är det lättare att följa fasta föremål som har naturliga gränser för att skilja dem från omgivningen.

Kinematiska beskrivningar

Eulerian approach I figuren indikerar den orange rutan intresseområdet. I det Euleriska tillvägagångssättet är platsen för den röda rutan fast, medan ändringen av färgen på den rutan illustrerar det ändrade värdet på den positionen.
Lagrangianskt tillvägagångssätt. I figuren indikerar den orange rutan intresseområdet. I det lagrangiska tillvägagångssättet är platsen för den röda rutan inte fixerad, den rör sig över tiden. Intresseområdet är alltid samma element.

Styrande ekvationer

Nedan följer några grundläggande ekvationer som vanligtvis används för att beskriva fysiska fenomen, till exempel hur materia i ett geologiskt system rör sig eller flyter och hur värmeenergin fördelas i ett system. Dessa ekvationer är vanligtvis kärnan i den matematiska modellen.

Kontinuitetsekvation

Kontinuitetsekvationen är en matematisk version av att det geologiska objektet eller mediet är kontinuerligt, vilket innebär att inget tomt utrymme kan hittas i objektet. Denna ekvation används ofta i numerisk modellering inom geologi.

Ett exempel är kontinuitetsekvationen för vätskans massa. Baserat på lagen om bevarande av massa , för en vätska med densitet $\rho$ i position $x_{j}$ i en fast volym $V$ av vätska, förändringshastigheten massan är lika med det utåtriktade vätskeflödet över gränsen $S$ :

${\frac {\partial }{\partial t}}\int \limits _{V}\rho d\tau =-\ int \limits _{S}\rho u_{j}dS_{j}$

där $\tau$ är volymelementet och $u_{j}$ är hastigheten vid $x_{j}$ .

I lagrangisk form:

${\frac {D\rho }{Dt}}\equiv {\frac {\partial \ rho }{\partial t}}+u_{j}{\frac {\partial \rho }{\partial x_{j}}}=-\rho {\frac {\partial u_{j}}{\partial x_ {j}}}$

I Eulerisk form:

${\frac {\partial \rho }{\partial t}}={\frac {\partial (\rho u_{j})}{\ partiell x_{j}}}$

Denna ekvation är användbar när modellen involverar kontinuerligt vätskeflöde, som att manteln är över geologiska tidsskalor.

Momentum ekvation

Momentumekvationen beskriver hur materia rör sig som svar på kraft som appliceras. Det är ett uttryck för Newtons andra rörelselag .

Betrakta en fast volym $V$ av materia. Enligt lagen om bevarande av momentum är volymförändringshastigheten lika med:

extern kraft $F$ applicerad på elementet
plus normal spänning och skjuvspänning applicerad på ytan $S$ som avgränsar elementet
minus momentum som rör sig ut ur elementet på den ytan

${\frac {\partial }{\ partiell t}}\int \limits _{V}\rho u_{i}d\tau =\int \limits _{V}\rho F_{i}d\tau +\int \limits _{S}\sigma _{ij}dS_{j}-\int \limits _{S}\rho u_{i}u_{j}dS_{j}$

där $\tau$ är volymelementet, $u$ är hastigheten.

Efter förenklingar och integrationer, för valfri volym $V$ , är den Euleriska formen av denna ekvation:

$\rho {\frac {\partial u_{i}}{\partial t}} +\rho u_{j}{\frac {\partial u_{i}}{\partial x_{j}}}=\rho F_{i}+{\frac {\partial \sigma _{ij}}{\ partiell x_{j}}}$

Värmeekvationen

Värmeekvationerna beskriver hur värmeenergi flyter i ett system.

Från lagen om energibevarande är förändringshastigheten för energi $E$ för en fast volym $V$ av massa lika med:

arbete utfört vid gränsen $S$
plus arbete utfört av extern kraft $F$ i volymen $V$
minus värmeledning över gränsen $S$
minus värmekonvektion över gränsen $S$
plus värme som produceras internt

Matematiskt:

${\frac {\partial }{\partial t}}\int \limits _{V}\rho Ed\tau =\int \limits _{S}u_{i }\sigma _{ij}dS_{j}+\int \limits _{V}\rho u_{i}F_{i}d\tau -\int \limits _{S}k{\frac {\partial T }{\partial x_{j}}}dS_{j}-\int \limits _{S}\rho Eu_{j}dS_{j}+\int \limits _{V}\rho Hd\tau$

där $\tau$ är volymelementet, $u$ är hastigheten, $T$ är temperaturen, $k$ är ledningskoefficienten och $H$ är värmeproduktionens hastighet.

Numeriska metoder

Ett exempel på 2D finita element mesh. Domänen är uppdelad i många icke-överlappande trianglar (element). Noder är trianglarnas hörn .

Numeriska metoder är tekniker för att approximera de styrande ekvationerna i de matematiska modellerna.

Vanliga numeriska metoder inkluderar finita elementmetoden , spektralmetoden , finita differensmetoden och finita volymmetoden . Dessa metoder används för att approximera lösningen av styrande differentialekvationer i den matematiska modellen genom att dissekera domänen i maskor eller rutnät och tillämpa enklare ekvationer på enskilda element eller noder i nätet.

Approximera vågekvationer med finita elementmetoden. Domänen är uppdelad i flera trianglar. Värdena för noderna i nätet beräknas och visar hur en våg fortplantar sig i regionen.

Metoden med diskreta element använder ett annat tillvägagångssätt. Objektet anses vara en sammansättning av små partiklar.

Finita elementmetod

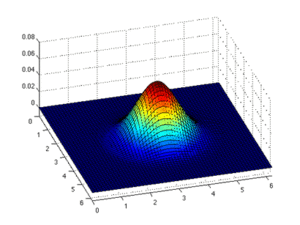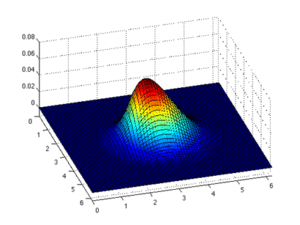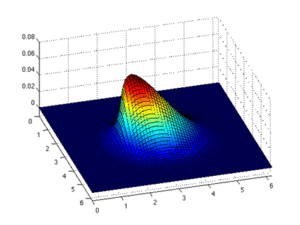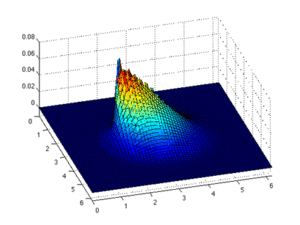
Den finita elementmetoden delar upp objektet (eller domänen) i mindre, icke-överlappande element (eller underdomäner) och dessa element är anslutna vid noderna. Lösningen för de partiella differentialekvationerna approximeras sedan med enklare elementekvationer, vanligtvis polynom . Sedan kombineras dessa elementekvationer till ekvationer för hela objektet, dvs bidraget från varje element summeras för att modellera hela objektets respons. Denna metod används ofta för att lösa mekaniska problem. Följande är de allmänna stegen för att använda finita elementmetoden:

Välj elementtyp och dela in objektet. Vanliga elementtyper inkluderar triangulära, fyrsidiga, tetraedriska, etc. Olika typer av element bör väljas för olika problem.
Bestäm förskjutningens funktion. Förskjutningens funktion styr hur elementen rör sig. Linjära, kvadratiska eller kubiska polynomfunktioner används vanligtvis.
Bestäm förskjutnings-töjningsrelationen. Förskjutningen av elementet ändrar eller deformerar elementets form i vad som tekniskt kallas töjning . Denna relation beräknar hur mycket påkänning elementet upplevde på grund av förskjutningen.
Bestäm belastning-stress-relationen. Deformationen av elementet inducerar spänning på elementet, vilket är kraften som appliceras på elementet. Denna relation beräknar mängden spänning som upplevs av elementet på grund av töjningen. Ett av exemplen på detta förhållande är Hookes lag .
Härled ekvationer av styvhet och styvhetsmatris för element. Spänningen gör också att elementet deformeras; styvheten (styvheten) hos elementen indikerar hur mycket den kommer att deformeras som svar på påkänningen . Styvheten hos elementen i olika riktningar är representerad i matrisform för enklare drift under beräkningen.
Kombinera elementekvationerna till globala ekvationer. Bidragen från varje element summeras till en uppsättning ekvationer som beskriver hela systemet.
Tillämpa gränsvillkor. De fördefinierade förhållandena vid gränsen, såsom temperatur, stress och andra fysiska storheter, introduceras till systemets gräns.
Lös för förskjutning. Allt eftersom tiden utvecklas löses förskjutningen av elementen steg för steg.
Lös för påfrestningar och stress. Efter att förskjutningen har beräknats, beräknas töjningarna och spänningen med hjälp av relationerna i steg 3 och 4.

Solution of Burgers Equation , som beskriver hur stötvågor beter sig, med hjälp av spektral metod . Domänen är först uppdelad i rektangulärt nät. Idén med denna metod liknar den finita elementmetoden.

Spektral metod

Den spektrala metoden liknar den finita elementmetoden. Den stora skillnaden är att spektralmetoden använder basfunktioner , möjligen genom att använda en Fast Fourier Transformation (FFT) som approximerar funktionen med summan av många enkla funktioner. Dessa typer av basfunktioner kan sedan appliceras på hela domänen och approximera de styrande partiella differentialekvationerna . Därför tar varje beräkning informationen från hela domänen i beräkningen medan finita elementmetoden endast tar informationen från grannskapet. Som ett resultat konvergerar den spektrala metoden exponentiellt och är lämplig för att lösa problem som involverar en hög variabilitet i tid eller rum.

Metod med ändlig volym

Den finita volymmetoden liknar också den finita elementmetoden. Den delar också upp föremålet av intresse i mindre volymer (eller element), sedan löses de fysiska kvantiteterna över kontrollvolymen som flöden av dessa kvantiteter över de olika ytorna. Ekvationerna som används är vanligtvis baserade på bevarandet eller balansen av fysiska storheter, som massa och energi.

Den finita volymmetoden kan tillämpas på oregelbundna maskor som finita elementmetoden. Elementekvationerna är fortfarande fysiskt meningsfulla. Det är dock svårt att få bättre noggrannhet, eftersom den högre ordningens versionen av elementekvationer inte är väldefinierade.

Ändlig skillnadsmetod

Den finita differensmetoden approximerar differentialekvationer genom att approximera derivatan med en differensekvation , vilket är huvudmetoden för att lösa partiella differentialekvationer .

Ändlig skillnadsmetod

Betrakta en funktion $f(x)$ med envärdiga derivator som är kontinuerliga och finita funktioner av $x$ , enligt Taylors teorem :

$f(x+ \Delta x)=f(x)+\Delta xf'(x)+{\frac {1}{2}}\Delta x^{2}f''(x)+{\frac {1}{6 }}\Delta x^{3}f'''(x)+\cdots$

och

$f(x -\Delta x)=f(x)-\Delta xf'(x)+{\frac {1}{2}}\Delta x^{2}f''(x)-{\frac {1}{ 6}}\Delta x^{3}f'''(x)+\cdots$

Sammanfattning av uttrycken ovan:

$f(x+\Delta x) +f(x-\Delta x)=2f(x)+\Delta x^{2}f''(x)+{\text{termer med högre än 4:e potens av }}\Delta x$

Ignorera termerna med högre än 4:e potens av $x$ och sedan:

$f''(x)\simeq {\frac {1} {\Delta x^{2}}}\left[f(x+\Delta x)-2f(x)-f(x-\Delta x)\right]$

$f'(x)\simeq {\frac {1}{2\Delta x}} \vänster[f(x+\Delta x)-f(x-\Delta x)\höger]$

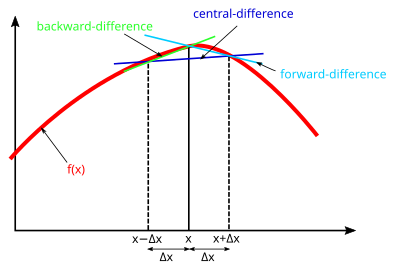
Ovanstående är approximationen av den centrala differensen för derivaten, som också kan approximeras med framåtriktad differens :

$f'(x)\simeq {\frac {1}{\Delta x}}\left[f( x+\Delta x)-f(x)\höger]$

eller bakåtskillnad :

$f'(x)\simeq {\frac {1}{\Delta x}}\left[f( x)-f(x-\Delta x)\höger]$

Noggrannheten hos de ändliga skillnaderna kan förbättras när fler termer av högre ordning används.

Diskret elementmetod

Ett exempel på modell som använder diskret elementmetod, som använder foto av Peter A. Cundall för att initiera partiklarna

Den diskreta elementmetoden , ibland kallad distinkt elementmetoden, används vanligtvis för att modellera diskontinuerliga material, såsom stenar med sprickor som fogar och strö, eftersom den explicit kan modellera diskontinuiteternas egenskaper. Denna metod utvecklades för att simulera bergmekaniska problem i början.

Huvudidén med denna metod är att modellera föremålen som en samling av mindre partiklar, vilket liknar att bygga ett slott av sand . Dessa partiklar är av enkel geometri, såsom en sfär. De fysiska kvantiteterna av varje partikel, såsom hastighet, uppdateras kontinuerligt vid kontakterna mellan dem. Denna modell är relativt beräkningsintensiv, eftersom en stor mängd partiklar måste användas, särskilt för storskaliga modeller, som en sluttning. Därför tillämpas denna modell vanligtvis på småskaliga föremål.

Bonded-partikel modell

Det finns föremål som inte är sammansatta av granulära material, till exempel kristallina bergarter som består av mineralkorn som fastnar vid varandra eller låser sig med varandra. Viss bindning mellan partiklar läggs till för att modellera denna kohesion eller cementering mellan partiklar. Denna typ av modell kallas också en bunden-partikelmodell.

Ansökningar

Numerisk modellering kan användas för att modellera problem inom olika områden av geologi på olika skalor, såsom ingenjörsgeologi , geofysik , geomekanik , geodynamik , bergmekanik , hydrogeologi och stratigrafi . Följande är några exempel på tillämpningar av numerisk modellering inom geologi.

Prov för att bryta skala

Bergmekanik

Numerisk modellering har använts i stor utsträckning inom olika områden av bergmekanik . Berg är ett material som är svårt att modellera eftersom berg vanligtvis är:

Diskontinuerlig : Det finns många sprickor och mikrosprickor i en bergmassa och utrymmet i bergmassan kan vara fyllt med andra ämnen som luft och vatten. En komplex modell behövs för att helt fånga dessa diskontinuiteter, eftersom diskontinuiteterna har stora effekter på bergmassan.
Anisotropisk : Bergmassans egenskaper, såsom permeabilitet (förmågan att tillåta vätska att strömma igenom), kan variera i olika riktningar.
Inhomogen : Egenskaperna för olika delar av bergmassan kan vara olika. Till exempel är de fysikaliska egenskaperna hos kvartskorn och fältspatkorn olika i granit .
Ej elastisk : Berget kan inte helt återgå till sin ursprungliga form efter att spänningen har tagits bort.

För att modellera bergets beteenden behövs en komplex modell som tar hänsyn till alla ovanstående egenskaper. Det finns många modeller som modellerar berget som ett kontinuum med metoder som finita skillnader , finita element och gränselementmetoder . En av nackdelarna är att förmågan att modellera sprickor och andra diskontinuiteter vanligtvis är begränsad i dessa modeller. Modeller som modellerar berg som ett diskontinuum, med metoder som diskreta element och diskreta spricknätsmetoder, används också ofta. Kombinationer av båda metoderna har också utvecklats.

Numerisk modellering förbättrar förståelsen för mekaniska processer i berg genom att utföra numeriska experiment, och är användbar för konstruktions- och konstruktionsarbeten.

Regional skala

Termokronologi

Numerisk modellering har använts för att förutsäga och beskriva den termiska historien för jordskorpan, vilket gör att geologer kan förbättra sin tolkning av termokronologiska data. Termokronologi kan indikera tidpunkten då en sten kyls under en viss temperatur. Geologiska händelser, som utvecklingen av förkastningar och yterosion, kan förändra det termokronologiska mönstret för prover som samlas in på ytan, och det är möjligt att begränsa de geologiska händelserna med dessa data. Numerisk modellering kan användas för att förutsäga mönstret.

Svårigheterna med termisk modellering av jordskorpan involverar främst oregelbundenheter och förändringar av jordens yta (främst erosion ) genom tiden. Därför, för att modellera de morfologiska förändringarna av jordens yta, behöver modellerna lösa värmeekvationer med randvillkor som förändras med tiden och har oregelbundna maskor.

Pecube

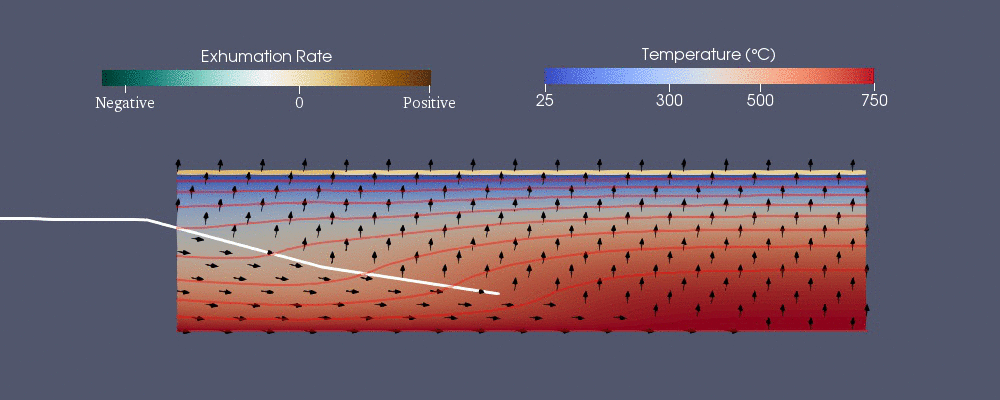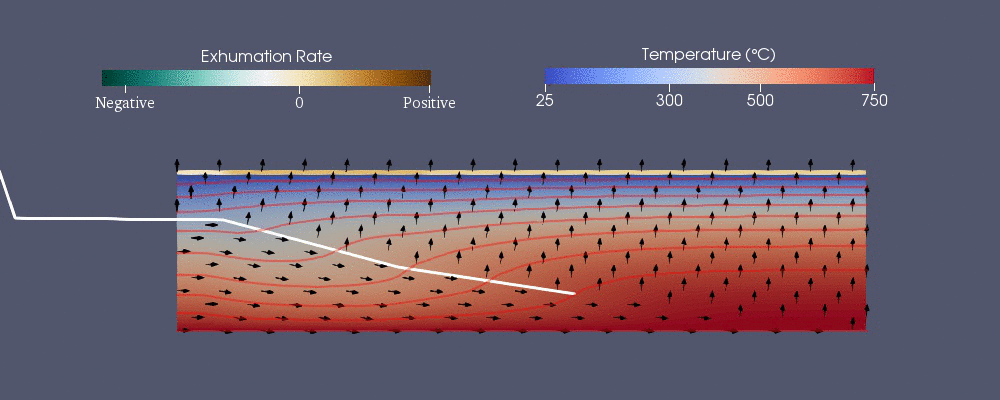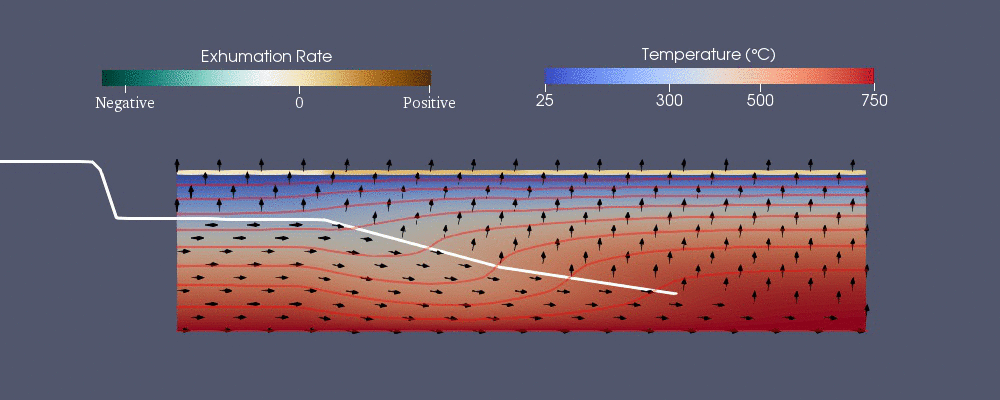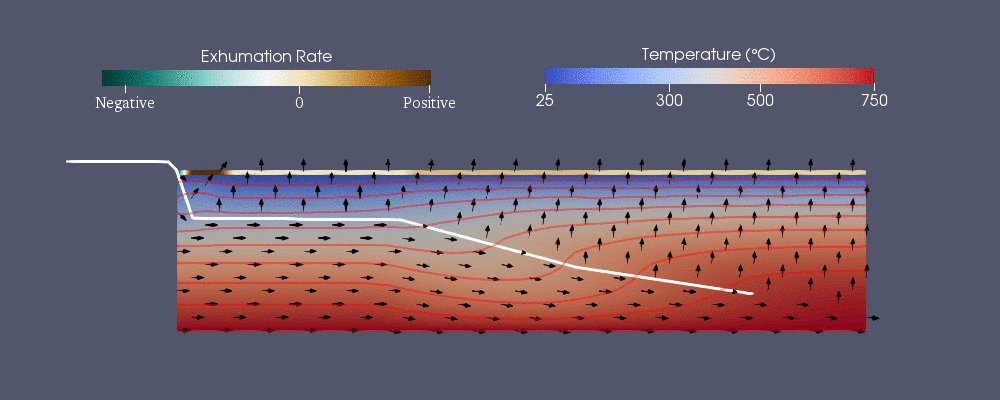
Pecube är en av de numeriska modellerna som utvecklats för att förutsäga det termokronologiska mönstret. Den löser följande generaliserade värmeöverföringsekvation med advektion med finita elementmetoden. De första tre termerna på höger sida är värmen som överförs genom ledning i $x$ , $y$ och $z$ -riktningarna medan $A$ är advektionen.

{\frac {\partial T}{\partial t}}+u{\frac {\partial T}{\partial x}}+v{\frac {\partial T}{\partial y}} +w{\frac {\partial T}{\partial z}}={\frac {\partial }{\partial x}}\kappa {\frac {\partial T}{\partial x}}+{\frac {\partial }{\partial y}}\kappa {\frac {\partial T}{\partial y}}+{\frac {\partial }{\partial z}}\kappa {\frac {\partial T} {\partial z}}+A

Efter att temperaturfältet har konstruerats i modellen spåras partikelvägar och partiklarnas kylhistorik kan erhållas. Mönstret för termokronologisk ålder kan sedan beräknas.

Ett tvärsnitt som visar skorpans termiska mönster och exhumationsmönster som genereras av ett fels rörelse . Simuleringen genereras av Pecube [versionen av Helsinki University Geodynamics Group (HUGG)]. Modellen är tredimensionell; figuren visar en del av modellen för enkelhets skull. I figuren indikerar den vita linjen felet . De små svarta pilarna indikerar materialets rörelseriktning vid den punkten. De röda linjerna är isoterma (punkten på linjen har samma temperatur). Pecube-modellen använder både Eulerian och Lagrangian approach. Felet kan betraktas som stationärt och skorpan rör sig. Till en början beror skorpans temperatur på djupet. Ju djupare djup, desto varmare material. Under denna händelse flyttar skorpans rörelse längs förkastningen materialet med olika temperaturer. I den hängande väggen (blocket ovanför förkastningen) rör sig hetare material från djupare djup mot ytan; medan det kallare materialet på grundare djup i fotväggen (blocket under förkastningen) rör sig djupare. Materialflödet ändrar det termiska mönstret (isotermen böjer sig över förkastningen) i jordskorpan, vilket kan återställa termokronometrarna i berget. Å andra sidan uppgrävningshastigheten även termokronometrarna i berget. En positiv uppgrävningshastighet indikerar att stenen rör sig mot ytan, medan en negativ uppgrävningshastighet indikerar att stenen rör sig nedåt. Felgeometrin påverkar mönsteruppgrävningshastigheten på ytan.

Hydrogeologi

Inom hydrogeologi modelleras grundvattenflödet ofta numeriskt med finita elementmetoden och finita differensmetoden. Dessa två metoder har visat sig ge liknande resultat om nätet är tillräckligt bra.

Finita skillnadsrutnät som används i MODFLOW

MODFLOW

Ett av de välkända programmen för att modellera grundvattenflöde är MODFLOW , utvecklat av United States Geological Survey . Det är ett gratis och öppen källkodsprogram som använder finita skillnadsmetoden som ramverk för att modellera grundvattenförhållanden. Den senaste utvecklingen av relaterade program erbjuder fler funktioner, inklusive:

Interaktioner mellan grundvatten och ytvattensystem
Transport av lösta ämnen
Flöde av vätska med variabel densitet, såsom saltvatten
Packning av akvifersystem
Marksättningar
Hantering av grundvatten

Skorpans dynamik

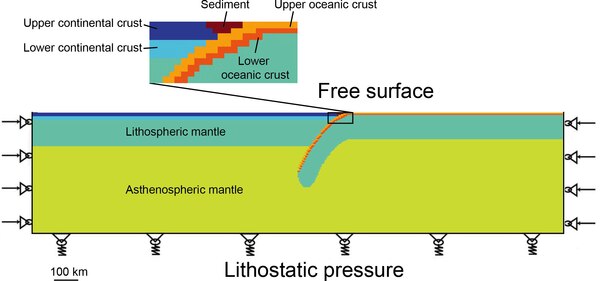
reologi (respons av material på spänningar) är komplex, eftersom en fri yta (landytan) och jordskorpans plasticitet och elasticitet måste beaktas. De flesta av modellerna använder finita elementmetoder med ett lagrangiskt nät. En användning är studiet av deformation och kinematik för subduktion .

FLAC

Fast Lagrangian Analysis of Continua (FLAC) är en av de mest populära metoderna för modellering av jordskorpans dynamik. Tillvägagångssättet är snabbt eftersom det löser ekvationerna av momentum och kontinuitet utan att använda en matris, därför är det snabbt men tidsstegen måste vara tillräckligt små. Metoden har använts i 2D-, 2,5D- och 3D-studier av jordskorpans dynamik, där 2,5D-resultaten genererades genom att kombinera flera segment av tvådimensionella resultat.

Den här figuren visar uppställningen av den numeriska modellen som används i studien av tektonisk utveckling av Cathaysia-blocket , som utgör den sydöstra delen av kartongen i Sydkina . Denna modell använder koden som kallas Flamar , som är en FLAC-liknande kod som kombinerar finita skillnad och finita elementmetoder. Elementet som används i detta lagrangiska nät är fyrsidigt. De gränsförhållanden som tillämpas på markytan är fria, vilket påverkas av erosion och sedimentavlagringar. Gränsen på sidorna är med konstant hastighet, vilket kommer att pressa skorpan att subducera . Det gränsvillkor som används i botten kallas "Winklers böjliga källare". Den är i hydrostatisk jämvikt och den låter basen glida fritt horisontellt.

Global skala

Mantelkonvektion

En simulering av mantelkonvektion i form av en fjärdedel av 2D-ring med hjälp av ASPECT . I modellen är temperaturen på gränsen mellan kärnan och manteln (inre gränsen) en konstant på 4273 K (cirka 4000 ℃), medan den vid gränsen mellan skorpan och manteln (yttre gränsen) är 973 K (cirka 700 ℃). Nätet i simuleringen förändras över tiden. Koden använder adaptiv nätförfining , nätet är finare i de områden som behöver mer exakt beräkning, såsom de stigande plymerna, medan nätet är grövre i andra områden för att spara beräkningskraften. I figuren indikerar röd färg en varmare temperatur medan blå färg indikerar en svalare temperatur; hett material stiger från kärnmantelns gräns på grund av lägre densitet. När det varma materialet når den yttre gränsen börjar det röra sig in horisontellt och sjunker så småningom på grund av kylning.

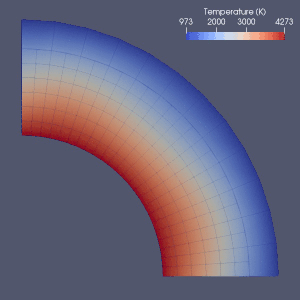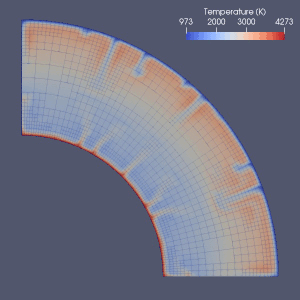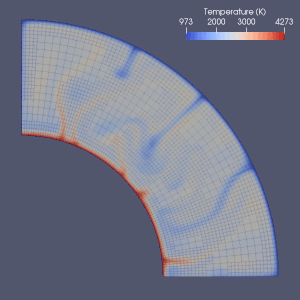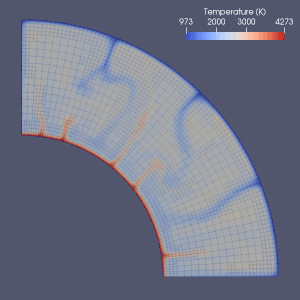
Det finns många försök att modellera mantelkonvektion.

Finita element , finit volym , finit skillnad och spektrala metoder har alla använts för att modellera mantelkonvektion, och nästan varje modell använde ett Eulerian rutnät. På grund av enkelheten och hastigheten hos metoderna med ändlig differens och spektral användes de i vissa tidiga modeller, men metoder med ändliga element eller ändliga volymer antogs i allmänhet på 2010-talet. Många riktmärken har undersökt giltigheten av dessa numeriska modeller. Nuvarande tillvägagångssätt använder oftast ett fast och enhetligt rutnät. Nätförfining, där storleken på elementen minskas i den del som kräver mer exakt approximation, är möjligen riktningen för framtida utveckling inom numerisk modellering av mantelkonvektion.

Tillvägagångssätt med ändlig skillnad

På 1960-talet till 1970-talet använde mantelkonvektionsmodeller som använde finita skillnadsmetoden vanligtvis andra ordningens finita skillnader . Strömningsfunktioner användes för att ta bort effekten av tryck och minska komplexiteten i algoritmen. På grund av framstegen inom datorteknik används nu ändliga skillnader med termer av högre ordning för att generera ett mer exakt resultat.

Tillvägagångssätt med ändlig volym

Mantelkonvektion modellerad med finita volymmetoder är ofta baserad på balansen mellan tryck och momentum . De härledda ekvationerna är desamma som tillvägagångssättet med ändlig skillnad med hjälp av ett rutnät med förskjuten hastighet och tryck, där värdena för hastighet och trycket för varje element är placerade vid olika punkter. Detta tillvägagångssätt kan upprätthålla kopplingen mellan hastighet och tryck.

Flera koder utvecklas baserat på detta tillvägagångssätt med ändlig skillnad/ändlig volym. Vid modellering av jordens tredimensionella geometri, eftersom parametrarna för mantlar varierar i olika skalor, används multigrid , vilket innebär att man använder olika rutnätsstorlekar för olika variabler, för att övervinna svårigheterna. Exempel inkluderar rutnätet med kubformade sfärer, "Yin-Yang"-rutnät och spiralrutnät.

Finita element tillvägagångssätt

I finita elementmetoden används ofta strömfunktioner för att reducera ekvationernas komplexitet. ConMan, som modellerar tvådimensionellt inkompressibelt flöde i manteln, var en av de populära koderna för modellering av mantelkonvektion på 1990-talet. Citcom , en Eulerian mutlgrid finita element-modell, är ett av de mest populära programmen för att modellera mantelkonvektion i 2D och 3D.

Spektral metod

Den spektrala metoden i mantelkonvektion bryter ner den tredimensionella styrande ekvationen i flera endimensionella ekvationer, vilket löser ekvationerna mycket snabbare. Det var ett av de populära tillvägagångssätten i tidiga modeller av mantelkonvektion. Många program utvecklades med denna metod under 1980-talet till början av 2000-talet. Men de laterala förändringarna av viskositet hos manteln är svåra att hantera i detta tillvägagångssätt, och andra metoder blev mer populära på 2010-talet.

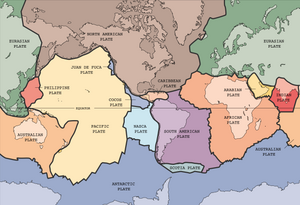
Jorden består av flera plattor. Numeriska modeller kan användas för att modellera plattornas kinematik.

Platttektonik

Plattektonik är en teori som tyder på att jordens litosfär i huvudsak består av plattor som flyter på manteln. Mantelkonvektionsmodellen är grundläggande för att modellera plattorna som flyter på den, och det finns två huvudsakliga tillvägagångssätt för att införliva plattorna i denna modell: styvt block-tillvägagångssätt och reologiskt tillvägagångssätt. Den stela blockmetoden förutsätter att plattorna är styva, vilket innebär att plattorna behåller sin form och inte deformeras, precis som vissa träblock flyter på vatten. Däremot modellerar det reologiska tillvägagångssättet plattorna som en mycket viskös vätska där ekvationerna som appliceras på litosfären under också gäller för plattorna ovanpå.

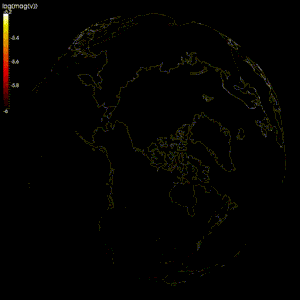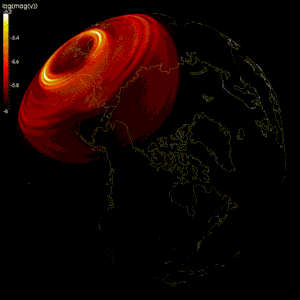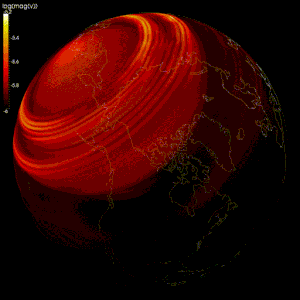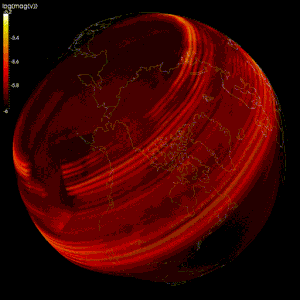
Geodynamo

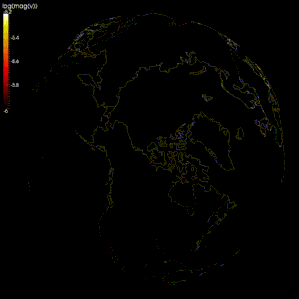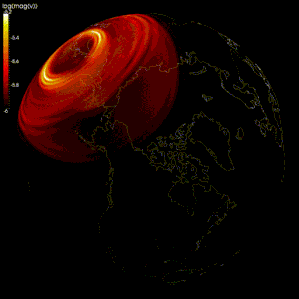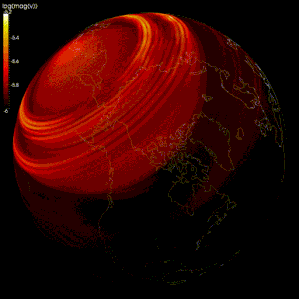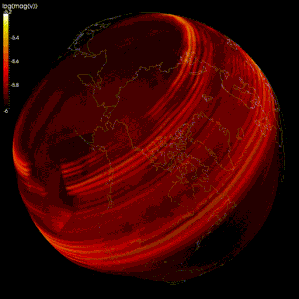
Numeriska modeller har gjorts för att verifiera geodynamo-teorin , en teori som hävdar att det geomagnetiska fältet alstras av rörelsen av ledande järn och nickelvätska i jordens kärna .

Modellering av flödet av jordens flytande yttre kärna är svårt eftersom:

Corioliseffekten på grund av jordens rotation kan inte ignoreras
det magnetiska fältet som genereras kommer också att generera Lorentzkraft , vilket kommer att påverka rörelsen av den ledande vätskan i den flytande yttre kärnan
den låga viskositeten hos flytande järn gör att vätskan flyter svårt att modellera

De flesta av modellerna använder den spektrala metoden för att simulera geodynamo, till exempel Glatzmaier-Roberts modellen. Finita different method har också använts i modellen av Kageyama och Sato. Vissa studier prövade också andra metoder, som finit volym och finita elementmetoder.

En numerisk geodynamomodell (Glatzmaier-Roberts modell) som visar det magnetiska fältet som genereras av den strömmande vätskekärnan. Denna figur visar hur jordens magnetfält beter sig under en magnetisk omkastning .

Seismologi

Simulering av seismisk vågutbredning genom jorden.

Finita skillnadsmetoder har använts i stor utsträckning i simuleringar av utbredningen av seismiska vågor . Men på grund av begränsningar i beräkningskraft, i vissa modeller, är avståndet mellan nätet för stort (jämfört med våglängden på de seismiska vågorna) så att resultaten är felaktiga på grund av rutnätsspridning, där de seismiska vågorna vågar med olika frekvenser separat. Vissa forskare föreslår att man använder den spektrala metoden för att modellera seismisk vågutbredning.

Fel och begränsningar

Felkällor

Medan numerisk modellering ger korrekt kvantitativ uppskattning av geologiska problem, finns det alltid en skillnad mellan den faktiska observationen och modelleringsresultaten på grund av:

förenklingen av själva problemet när man bygger den numeriska modellen. Eftersom många faktorer kan påverka ett geologiskt system är det nästan omöjligt att ta hänsyn till allt. Därför förenklar en numerisk modell vanligtvis det faktiska systemet genom att utelämna de mindre signifikanta faktorerna. Till exempel modelleras jorden ofta som en sfär, trots att jordens yta är böljande.
approximationerna eller idealiseringarna av de styrande ekvationerna. Många föremål i naturen är komplexa. Det är omöjligt att fånga alla egenskaper med hjälp av ekvationer. Till exempel är bergarter diskontinuerliga , men att modellera berg som ett kontinuerligt material är rimligt i stor skala eftersom det beskriver egenskaperna tillräckligt noggrant.
approximationerna i diskretiseringsprocessen. Eftersom de styrande ekvationerna i modellen inte kan lösas direkt görs approximationer till dessa ekvationer med diskretisering och numeriska metoder.
osäkerheten i fysiska parametrar. Till exempel är modellerna av viskositeten för mantel och kärna inte korrekta.

Begränsningar

Förutom felen finns det vissa begränsningar i att använda numeriska modeller:

Användare av modellerna behöver hög kunskap och erfarenhet för att förhindra missbruk och feltolkning av resultat.

Se även