Klassificering av diskontinuiteter

"Jump point" omdirigerar hit. För science-fiction-konceptet, se Hyperspace .

Kontinuerliga funktioner är av yttersta vikt i matematik , funktioner och tillämpningar. Alla funktioner är dock inte kontinuerliga. Om en funktion inte är kontinuerlig vid en punkt i dess domän , säger man att den har en diskontinuitet där. Uppsättningen av alla diskontinuitetspunkter för en funktion kan vara en diskret uppsättning , en tät uppsättning eller till och med hela domänen av funktionen. Den här artikeln beskriver klassificeringen av diskontinuiteter i det enklaste fallet av funktioner för en enda reell variabel som tar reella värden.

Svängningen av en funktion vid en punkt kvantifierar dessa diskontinuiteter enligt följande:

• i en löstagbar diskontinuitet är det avstånd som värdet på funktionen är avstängt med svängningen;
• i en hoppdiskontinuitet är hoppets storlek svängningen (förutsatt att värdet vid punkten ligger mellan dessa gränser för de två sidorna);
• i en väsentlig diskontinuitet mäter oscillation att en gräns inte existerar; gränsen är konstant.

Ett specialfall är om funktionen divergerar till oändlighet eller minus oändlighet , i vilket fall oscillationen inte är definierad (i de utökade reella talen är detta en borttagbar diskontinuitet).

Klassificering

För vart och ett av följande, överväg en verkligt värderad funktion $f$ av en reell variabel $x,$ definierad i en grannskap av punkten $x_{0}$ där ${\ displaystyle f}$ är diskontinuerlig.

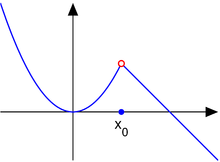
Avtagbar diskontinuitet

Funktionen i exempel 1, en borttagbar diskontinuitet

Tänk på den styckvisa funktionen

$$f(x)={\begin{cases}x^{2}&{\text{ för }} x<1\\0&{\text{ för }}x=1\\2-x&{\text{ för }}x>1\end{case}}$$

Punkten $x_{0}=1$ är en borttagbar diskontinuitet . För denna typ av diskontinuitet:

Den ensidiga gränsen från negativ riktning:

$$L^{-}=\lim _{x\to x_{0}^{-}}f(x)$$

och den ensidiga gränsen från den positiva riktningen:

$$L^{+}=\lim _{x\to x_{0}^{+}}f(x)$$

vid ${\displaystyle x_{0}} finns$ båda , är ändliga och är lika med $L=L^{-}=L^{+}.$ Med andra ord, eftersom de två ensidiga gränserna finns och är lika, gränsen $L$ för $f(x)$ när $x$ närmar sig $x_{0}$ och är lika med samma värde. Om det faktiska värdet av $f\left(x_{0}\right)$ inte är lika med $L,$ kallas $x_{0}$ en flyttbar diskontinuitet . Denna diskontinuitet kan tas bort för att göra $f$ kontinuerlig vid $x_{0},$ eller mer exakt, funktionen

$$g(x)={\begin{cases}f(x)&x\neq x_{0}\\L&x=x_{0} \end{cases}}$$

är kontinuerlig vid $x=x_{0}.$

Termen borttagbar diskontinuitet breddas ibland till att omfatta en borttagbar singularitet , där gränserna i båda riktningarna finns och är lika, medan funktionen är odefinierad vid punkten $x_{0}.$ Denna användning är ett missbruk av terminologi eftersom kontinuitet och diskontinuitet för en funktion är begrepp som endast definieras för punkter i funktionens domän.

Hoppdiskontinuitet

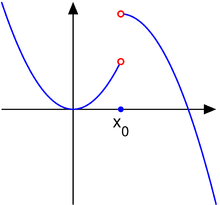
Funktionen i exempel 2, en hoppdiskontinuitet

Tänk på funktionen

$$f(x)={\begin{cases}x^{2}&{\ mbox{ för }}x<1\\0&{\mbox{ för }}x=1\\2-(x-1)^{2}&{\mbox{ för }}x>1\end{cases} }$$

Då är punkten $x_{0}=1$ en hoppdiskontinuitet .

I det här fallet existerar inte en enda gräns eftersom de ensidiga gränserna $L^{-}$ och $L^{+}$ existerar och är ändliga, men är inte lika: eftersom, $L^{-}\neq L^{+},$ existerar inte gränsen ${\displaystyle L} .$ Sedan kallas ${\displaystyle x_{0}} en$ hoppdiskontinuitet , stegdiskontinuitet eller diskontinuitet av det första slaget . För denna typ av diskontinuitet kan funktionen $f$ ha vilket värde som helst vid $x_{0}.$

Viktig diskontinuitet

Funktionen i exempel 3, en väsentlig diskontinuitet

För en väsentlig diskontinuitet finns inte minst en av de två ensidiga gränserna i $\mathbb {R}$ . (Observera att en eller båda ensidiga gränserna kan vara ${\displaystyle \pm \infty } )$ .

Tänk på funktionen

$$f(x)={\begin{cases}\sin {\frac {5 }{x-1}}&{\text{ för }}x<1\\0&{\text{ för }}x=1\\{\frac {1}{x-1}}&{\text{ för }}x>1.\end{cases}}$$

Då är punkten $x_{0}=1$ en väsentlig diskontinuitet .

I det här exemplet existerar inte både $L^{-}$ och ${\displaystyle L^{+}} i$$\mathbb {R}$ , vilket uppfyller villkoret för väsentlig diskontinuitet . Så $x_{0}$ är en väsentlig diskontinuitet, oändlig diskontinuitet eller diskontinuitet av det andra slaget. (Detta skiljer sig från en väsentlig singularitet , som ofta används när man studerar funktioner hos komplexa variabler ).

Om vi ​​antar att $f$ är en funktion definierad på ett intervall $I\subseteq \mathbb {R} ,$ kommer vi att beteckna med $D$ mängden av alla diskontinuiteter av ${ \displaystyle f}$ på $I.$ Med $R$ menar vi mängden av alla $x_{0}\in I$ så att $f$ har en borttagbar diskontinuitet vid $x_{0}.$ Analogt med $J$ betecknar vi mängden som utgörs av alla $x_{0}\in I}$ displaystyle så att $f$ har en hoppdiskontinuitet vid $x_{0}.$ Mängden av alla $x_{0}\in I$ så att $f$ har en väsentlig diskontinuitet vid $x_{0}$ betecknas $E.$ Naturligtvis då $D=R\cup J\cup E.$

Räkna diskontinuiteter för en funktion

De två följande egenskaperna för uppsättningen $D$ är relevanta i litteraturen.

• Mängden $D$ är en ${\displaystyle F_{\sigma }}-$ uppsättning . Mängden punkter där en funktion är kontinuerlig är alltid en $G_{\delta }$ uppsättning (se).

• Om på intervallet $I,$$f$ är monoton så är $D$ som mest räknebar och $D=J.$ Detta är Frodas sats .

Tom Apostol följer delvis klassificeringen ovan genom att endast överväga borttagning och hoppdiskontinuiteter. Hans mål är att studera diskontinuiteterna i monotona funktioner, främst för att bevisa Frodas teorem. Med samma syfte studerar Walter Rudin och Karl R. Stromberg också borttagnings- och hoppdiskontinuiteter genom att använda olika terminologier. Men vidare säger båda författarna att $R\cup J$ alltid är en räknebar mängd (se).

Termen väsentlig diskontinuitet verkar ha introducerats av John Klippert. Vidare klassificerade han också väsentliga diskontinuiteter själva genom att dela upp mängden $E$ i de tre följande uppsättningarna:

$$E_{1}=\left\{x_{0} \in I:\lim _{x\to x_{0}^{-}}f(x){\text{ och }}\lim _{x\to x_{0}^{+}}f(x ){\text{ finns inte i }}\mathbb {R} \right\},$$

$$E_{2}=\left\{x_ {0}\in I:\ \lim _{x\to x_{0}^{-}}f(x){\text{ finns i }}\mathbb {R} {\text{ och }}\lim _{x\to x_{0}^{+}}f(x){\text{ finns inte i }}\mathbb {R} \right\},$$

$$E_{3}=\left\{x_{0}\in I:\ \lim _{x\to x_{0}^{-}}f(x){\text{ finns inte i } }\mathbb {R} {\text{ och }}\lim _{x\to x_{0}^{+}}f(x){\text{ finns i }}\mathbb {R} \right\} .$$

Naturligtvis $E=E_{1}\cup E_{2}\cup E_{3}.$ När $x_{0}\in E_{1},$$x_{ 0}$ kallas en väsentlig diskontinuitet av första slag . Alla $x_{0}\in E_{2}\cup E_{3}$ sägs vara en väsentlig diskontinuitet av andra slag. Därför förstorar han mängden $R\cup J$ utan att förlora sin egenskap att vara räknebar, genom att ange följande:

• Uppsättningen $R\cup J\cup E_{2}\cup E_{3}$ kan räknas.

Omskrivning av Lebesgues sats

När $I=[a,b]$ och $f$ är en avgränsad funktion, är det välkänt om betydelsen av mängden $D$ i hänsyn till Riemann- integrerbarheten av $f.$ Faktum är att Lebesgues sats (även kallad Lebesgue-Vitali) sats) att $f$ är Riemann-integrerbar på $I=[a,b]$ om och endast om $D$ är en mängd med Lebesgues mått noll.

$[a,b].$ sats verkar det som att alla typer av diskontinuiteter har samma tyngd på hindret att en begränsad funktion $f$ är Riemann-integrerbar på Eftersom räknebara mängder är mängder av Lebesgues mått noll och en räknebar förening av mängder med Lebesgues mått noll fortfarande är en mängd av Lebesgues mått noll, ser vi nu att så inte är fallet. Faktum är att diskontinuiteterna i mängden $R\cup J\cup E_{2}\cup E_{3}$ är absolut neutrala när det gäller Riemann-integrerbarheten av $f.$ De huvudsakliga diskontinuiteterna för detta ändamål är de väsentliga diskontinuiteterna av första slag och följaktligen kan Lebesgue-Vitali-satsen skrivas om enligt följande:

• En avgränsad funktion, $f,$ är Riemann-integrerbar på $[a,b]$ om och endast om motsvarande uppsättning $E_{1}$ av alla väsentliga diskontinuiteter av första typen av $f$ har Lebesgues mått noll.

Fallet där $E_{1}=\varnothing$ motsvarar följande välkända klassiska komplementära situationer av Riemann-integrerbarhet av en begränsad funktion $f:[ a,b]\to \mathbb {R}$ :

• Om $f$ har högergräns vid varje punkt av $[a,b[$ så är $f$ Riemann-integrerbar på $[ a,b]$ (se)
• Om $f$ har vänstergräns vid varje punkt av $]a,b]$ så är $f$ Riemann-integrerbar på $[a,b].$
• Om $f$ är en reglerad funktion på $[a,b]$ så är $f$ Riemann-integrerbar på $[a,b].$

Exempel

Thomaes funktion är diskontinuerlig vid varje rationell punkt som inte är noll , men kontinuerlig vid varje irrationell punkt. Man ser lätt att dessa diskontinuiteter alla är väsentliga av det första slaget, det vill säga $E_{1}=\mathbb {Q} .$ Enligt det första stycket finns det inte en funktion som är kontinuerlig vid varje rationell punkt, utan diskontinuerlig vid varje irrationell punkt.

Rationalernas indikatorfunktion, även känd som Dirichlet -funktionen , är diskontinuerlig överallt . Dessa diskontinuiteter är också väsentliga av det första slaget.

Betrakta nu den ternära Cantor-mängden ${\mathcal {C}}\subset [0,1]$ och dess indikator- (eller karakteristiska) funktion

$$\mathbf {1} _{\mathcal {C}}(x)={\begin{cases}1&x\in {\mathcal {C}}\\0&x\notin [0,1]\setminus {\ mathcal {C}}.\end{cases}}$$

Ett sätt att konstruera Cantor-mängden ${\mathcal {C}}$ ges av ${\textstyle {\mathcal {C}}:=\bigcap _{n=0 }^{\infty }C_{n}}$ där mängderna $C_{n}$ erhålls genom återfall enl.

$$C_{n}={\frac {C_{n-1}}{3}}\cup \left({\frac {2}{3}}+{\frac {C_{n-1}} {3}}\right){\text{ för }}n\geq 1,{\text{ och }}C_{0}=[0,1].$$

Med tanke på diskontinuiteterna för funktionen $\mathbf {1} _{\mathcal {C}}(x),$ låt oss anta en punkt $x_{0}\inte \in {\mathcal {C}}.$

Därför finns det en mängd $C_{n},$ som används i formuleringen av ${\displaystyle {\mathcal {C}}} ,$ som inte innehåller $x_{0}.$ Det vill säga, $x_{0}$ tillhör ett av de öppna intervallen som togs bort i konstruktionen av $C_{n}.$ På detta sätt har $x_{0}$ en stadsdel utan punkter på ${\mathcal {C}}.$ (På ett annat sätt följer samma slutsats med hänsyn till att ${\mathcal {C}}$ är en sluten mängd och därför kompletterar den med avseende på $[0,1]$ är öppen). Därför $\mathbf {1} _{\mathcal {C}}$ endast värdet noll i någon omgivning av $x_{0}.$ Därför är $\mathbf {1} _{\mathcal {C}}$ kontinuerlig vid $x_{0}.$

Detta betyder att mängden $D$ av alla diskontinuiteter av $\mathbf {1} _{\mathcal {C}}$ på intervallet $[0,1]$ är en delmängd av ${\mathcal {C}}.$ Eftersom ${\mathcal {C}}$ är en icke-räknebar mängd med noll Lebesgue-mått , är även $D$ en noll Lebesgue-mått och så i hänsynen till Lebesgue-Vitali-sats $\mathbf {1} _{\mathcal {C}}$ är en Riemann-integrerbar funktion.

Mer exakt har man $D={\mathcal {C}}.$ Faktum är att eftersom ${\mathcal {C}}$ är en sällsynt (stängd eller tom interiör) uppsättning, om $x_{ 0}\i {\mathcal {C}}$ sedan ingen grannskap $\left(x_{0}-\varepsilon ,x_{0}+\varepsilon \right)$ av $x_{0},$ kan finnas i ${\mathcal {C}}.$ På detta sätt innehåller varje grannskap av $x_{0}\in {\mathcal {C}}$ punkter av ${\mathcal {C }}$ och punkter som inte är av ${\mathcal {C}}.$ När det gäller funktionen $\mathbf {1} _{\mathcal {C}}$ betyder detta att både ${\textstyle \lim _{x\to x_{0}^{-}}\mathbf {1} _{\mathcal {C}}(x)} och lim$ x $textstyle \lim _{x\to x_{0}^{+}}1_{\mathcal {C}}(x)}$ finns inte. Det vill säga, $D=E_{1},$ där vi med $E_{1},$ som tidigare betecknar mängden av alla väsentliga diskontinuiteter av den första typen av funktionen $\mathbf {1} _{\mathcal {C}}.$ Klart ${\textstyle \int _{0}^{1}\mathbf {1} _ {\mathcal {C}}(x)dx=0.}$

Diskontinuiteter av derivat

Låt nu $I\subseteq \mathbb {R}$ ett öppet intervall och $f:I\to \mathbb {R}$ derivatan av en funktion, $F:I\to \mathbb {R}$ , differentierbar på $I$ . Det vill säga $F'(x)=f(x)$ för varje $x\in I$ .

Det är välkänt att enligt Darboux' sats har derivatfunktionen $f:I\to \mathbb {R}$ begränsningen att tillfredsställa egenskapen mellanvärde.

$f$ kan givetvis vara kontinuerlig på intervallet $I$ . Kom ihåg att varje kontinuerlig funktion, enligt Bolzanos sats , uppfyller egenskapen mellanvärde.

Å andra sidan hindrar inte egenskapen mellanvärde att $f$ har diskontinuiteter på intervallet $I$ . Men Darboux' teorem har en omedelbar konsekvens på vilken typ av diskontinuiteter som $f$ kan ha. Faktum är att om $x_{0}\in I$ är en diskontinuitetspunkt för $f$ , så är nödvändigtvis $x_{0}$ en väsentlig diskontinuitet för ${\ displaystil f}$ .

Detta betyder särskilt att följande två situationer inte kan inträffa:

1. $x_{0}$ är en borttagbar diskontinuitet av $f$ .
2. $x_{0}$ är en hoppdiskontinuitet av $f$ .

Dessutom måste två andra situationer uteslutas (se John Klippert):

3. $\lim _{x\to x_{0}^{-}}f(x)=\pm \infty .$
4. $\lim _{x\to x_{0}^{+}}f(x)=\pm \infty .$

Observera att när ett av villkoren (i), (ii), (iii) eller (iv) är uppfyllt för vissa $x_{0}\in I$ kan man dra slutsatsen att $f$ saknar en antiderivata, $F$ , på intervallet $I$ .

Å andra sidan kan en ny typ av diskontinuitet med avseende på vilken funktion $f:I\to \mathbb {R}$ introduceras: en väsentlig diskontinuitet, $x_{ 0}\in I$ , av funktionen $f$ , sägs vara en grundläggande väsentlig diskontinuitet för $f$ om

$$\lim _{x\to x_{0}^{-}}f(x)\neq \pm \infty$$

och

$$\lim _{x\to x_{0}^{+}}f(x)\neq \pm \infty .$$

Därför om $x_{0}\in I$ är en diskontinuitet av en derivativ funktion $f:I\to \mathbb {R}$ , då nödvändigtvis $x_ {0}$ är en grundläggande väsentlig diskontinuitet för $f$ .

Lägg också märke till att när $I=[a,b]$ och $f:I\to \mathbb {R}$ är en begränsad funktion, som i antaganden av Lebesgues sats har vi för alla $x_{0}\in (a,b)$ :

$$\lim _{x\to x_{0}^{\pm }}f(x)\neq \pm \infty ,$$

$$\lim _{x\to a^{+}}f(x)\neq \pm \infty ,$$

och

$$\lim _{x\to b^{-}}f(x)\neq \pm \infty .$$

Därför är varje väsentlig diskontinuitet för $f$ en fundamental sådan.

Se även

• Borttagbar singularitet – Odefinierad punkt på en holomorf funktion som kan göras regelbunden
• Matematisk singularitet – Punkt där en funktion, en kurva eller ett annat matematiskt objekt inte beter sig regelbundet Sidor som visar korta beskrivningar av omdirigeringsmål
• Förlängning genom kontinuitet – topologiskt utrymme där en punkt och en sluten uppsättning är, om de är osammanhängande, separerade av stadsdelar Sidor som visar wikidata-beskrivningar som en reserv
• Jämnhet – Antal derivator av en funktion (matematik)
  • Geometrisk kontinuitet – Antal derivator av en funktion (matematik) Sidor som visar korta beskrivningar av omdirigeringsmål
  • Parametrisk kontinuitet – Antal derivator av en funktion (matematik) Sidor som visar korta beskrivningar av omdirigeringsmål

Källor

•   Malik, SC; Arora, Savita (1992). Matematisk analys (2:a uppl.). New York: Wiley. ISBN 0-470-21858-4 .

externa länkar

• "Diskontinuerlig" . PlanetMath .
• "Discontinuity" av Ed Pegg, Jr. , The Wolfram Demonstrations Project , 2007.
• Weisstein, Eric W. "Discontinuity" . MathWorld .
• Kudryavtsev, LD (2001) [1994]. "Diskontinuitetspunkt" . Encyclopedia of Mathematics . EMS Tryck på .