Kinetisk isotopeffekt

${\ displaystyle {\begin{matrix}\\{\ce {{CN^{-}}+{^{12}CH3-Br}->[k_{12}]{^{12}CH3-CN}+Br^ {-}}}\\{\ce {{CN^{-}}+{^{13}CH3-Br}->[k_{13}]{^{13}CH3-CN}+Br^{- }}}\\{}\end{matrix}}\qquad {\text{KIE}}={\frac {k_{12}}{k_{13}}}=1.082\pm 0.008}$

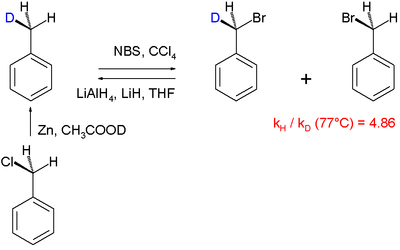
Ett exempel på den kinetiska isotopeffekten. I reaktionen mellan metylbromid och cyanid visade sig den kinetiska isotopeffekten av kolet i metylgruppen vara 1,082 ± 0,008 .

Inom fysikalisk organisk kemi är en kinetisk isotopeffekt ( KIE ) förändringen i reaktionshastigheten för en kemisk reaktion när en av atomerna i reaktanterna ersätts med en av dess isotoper . Formellt är det förhållandet mellan hastighetskonstanter för reaktionerna som involverar de lätta ( kL _{substituerade} ) och de tunga ( _kH ) isotopiskt reaktanterna (isotopologer):

${\text{KIE}}={\frac {k_{L}}{k_{H}}}$

Denna förändring i reaktionshastighet är en kvantmekanisk effekt som främst är resultatet av tyngre isotopologer som har lägre vibrationsfrekvenser jämfört med deras lättare motsvarigheter. I de flesta fall innebär detta en större energiinsats som behövs för att tyngre isotopologer ska nå övergångstillståndet ( eller, i sällsynta fall, dissociationsgränsen ) , och följaktligen en långsammare reaktionshastighet. Studiet av kinetiska isotopeffekter kan hjälpa till att klarlägga reaktionsmekanismen för vissa kemiska reaktioner och utnyttjas ibland i läkemedelsutveckling för att förbättra ogynnsam farmakokinetik genom att skydda metaboliskt känsliga CH-bindningar.

Bakgrund

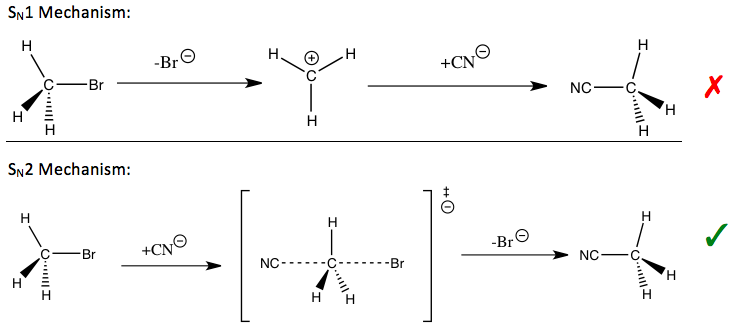
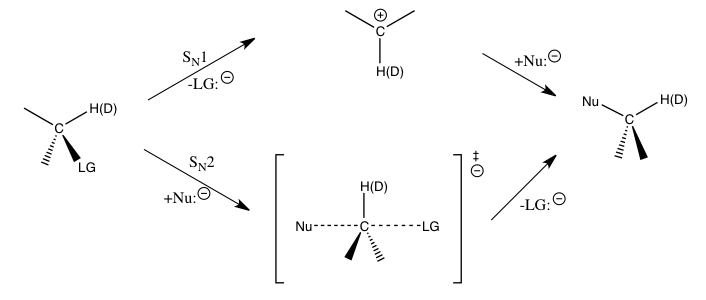
Den kinetiska isotopeffekten anses vara ett av de mest väsentliga och känsliga verktygen för att studera reaktionsmekanismer , vars kunskap möjliggör förbättring av de önskvärda egenskaperna hos motsvarande reaktioner. Till exempel kan kinetiska isotopeffekter användas för att avslöja om en nukleofil substitutionsreaktion följer en unimolekylär (S _N 1) eller bimolekylär ( _SN 2) väg.

I reaktionen mellan metylbromid och cyanid (visas i inledningen) indikerar den observerade kinetiska isotopeffekten av metylkol en S _N 2 -mekanism. Beroende på vägen kan olika strategier användas för att stabilisera övergångstillståndet för reaktionens hastighetsbestämmande steg och förbättra reaktionshastigheten och selektiviteten, vilket är viktigt för industriella tillämpningar.

Isotophastighetsförändringar är mest uttalade när den relativa massaförändringen är störst, eftersom effekten är relaterad till vibrationsfrekvenserna för de påverkade bindningarna. Till exempel, att ändra en väteatom (H) till dess isotop deuterium (D) representerar en 100% ökning av massan, medan om man ersätter kol -12 med kol-13, ökar massan med endast 8 procent. Hastigheten för en reaktion som involverar en C–H-bindning är vanligtvis 6–10 gånger snabbare än motsvarande C–D-bindning, medan en ¹² C-reaktion bara är 4 procent snabbare än motsvarande ¹³ C-reaktion (även om, i båda fallen, isotopen är en atommassenhet tyngre).

Isotopsubstitution kan modifiera reaktionshastigheten på en mängd olika sätt. I många fall kan hastighetsskillnaden rationaliseras genom att notera att en atoms massa påverkar vibrationsfrekvensen för den kemiska bindning som den bildar, även om den potentiella energiytan för reaktionen är nästan identisk. Tyngre isotoper kommer ( klassiskt ) att leda till lägre vibrationsfrekvenser, eller, sett kvantmekaniskt , kommer de att ha lägre nollpunktsenergi . Med en lägre nollpunktsenergi måste mer energi tillföras för att bryta bindningen, vilket resulterar i en högre aktiveringsenergi för bindningsklyvning, vilket i sin tur sänker den uppmätta hastigheten (se t.ex. Arrhenius-ekvationen ).

Klassificering

Primära kinetiska isotopeffekter

En primär kinetisk isotopeffekt kan hittas när en bindning till den isotopiskt märkta atomen bildas eller bryts. Beroende på hur en kinetisk isotopeffekt undersöks (parallell mätning av hastigheter kontra intermolekylär konkurrens kontra intramolekylär konkurrens), är observationen av en primär kinetisk isotopeffekt en indikation på att bryta/bilda en bindning till isotopen vid det hastighetsbegränsande steget eller efterföljande produktbestämmande steg. (Misuppfattningen att en primär kinetisk isotopeffekt måste återspegla bindningsklyvning/bildning till isotopen vid det hastighetsbegränsande steget upprepas ofta i läroböcker och primärlitteratur: se avsnittet om experiment nedan. )

För de tidigare nämnda nukleofila substitutionsreaktionerna har primära kinetiska isotopeffekter undersökts för både de lämnande grupperna, nukleofilerna och α-kolet vid vilket substitutionen sker. Tolkningen av den lämnande gruppens kinetiska isotopeffekter hade till en början varit svår på grund av betydande bidrag från temperaturoberoende faktorer. Kinetiska isotopeffekter vid α-kolet kan användas för att utveckla en viss förståelse för symmetrin av övergångstillståndet i S _N 2 -reaktioner, även om denna kinetiska isotopeffekt är mindre känslig än vad som skulle vara idealiskt, också på grund av bidrag från icke-vibrerande faktorer.

Sekundära kinetiska isotopeffekter

En sekundär kinetisk isotopeffekt observeras när ingen bindning till den isotopiskt märkta atomen i reaktanten bryts eller bildas. Sekundära kinetiska isotopeffekter tenderar att vara mycket mindre än primära kinetiska isotopeffekter; sekundära deuteriumisotopeffekter kan dock vara så stora som 1,4 per deuteriumatom, och tekniker har utvecklats för att mäta tunga elementisotopeffekter med mycket hög precision, så sekundära kinetiska isotopeffekter är fortfarande mycket användbara för att belysa reaktionsmekanismer.

För de tidigare nämnda nukleofila substitutionsreaktionerna ger sekundära kinetiska isotopeffekter av väte vid a-kolet ett direkt sätt att skilja mellan S _N 1 och S _N 2 reaktioner. Det har visat sig att S _N 1-reaktioner typiskt leder till stora sekundära kinetiska isotopeffekter, som närmar sig sitt teoretiska maximum vid cirka 1,22, medan S _N 2-reaktioner typiskt ger primära kinetiska isotopeffekter som är mycket nära eller mindre än enhet. Kinetiska isotopeffekter som är större än 1 kallas normala kinetiska isotopeffekter , medan kinetiska isotopeffekter som är mindre än en kallas omvända kinetiska isotopeffekter . I allmänhet förväntas mindre kraftkonstanter i övergångstillståndet ge en normal kinetisk isotopeffekt, och större kraftkonstanter i övergångstillståndet förväntas ge en invers kinetisk isotopeffekt när sträckande vibrationsbidrag dominerar den kinetiska isotopeffekten.

Storleken på sådana sekundära isotopeffekter vid a-kolatomen bestäms till stor del av C _α -H(D) vibrationerna. För en S _N 1-reaktion, eftersom kolatomen omvandlas till en sp ² -hybridiserad karbeniumjon under övergångstillståndet för det hastighetsbestämmande steget med en ökning av C _α -H(D) bindningsordningen, skulle en invers kinetisk isotopeffekt förväntas om bara sträckvibrationerna var viktiga. De observerade stora normala kinetiska isotopeffekterna har visat sig vara orsakade av betydande vibrationsbidrag utanför planet vid böjning när de går från reaktanterna till övergångstillståndet för karbeniumjonbildning. För S _N 2-reaktioner spelar böjningsvibrationer fortfarande en viktig roll för den kinetiska isotopeffekten, men sträckande vibrationsbidrag är av mer jämförbar storlek, och den resulterande kinetiska isotopeffekten kan vara normal eller omvänd beroende på de specifika bidragen från respektive vibrationer.

Teori

Den teoretiska behandlingen av isotopeffekter bygger i hög grad på teorin om övergångstillstånd , som antar en enda potentiell energiyta för reaktionen, och en barriär mellan reaktanterna och produkterna på denna yta, ovanpå vilken övergångstillståndet ligger. Den kinetiska isotopeffekten härrör till stor del från förändringarna i vibrationsgrundtillstånd som produceras av den isotopiska störningen längs den potentiella energiytans minimienergiväg, vilket endast kan förklaras med kvantmekaniska behandlingar av systemet. Beroende på massan av atomen som rör sig längs reaktionskoordinaten och arten (bredd och höjd) av energibarriären, kvantmekanisk tunnling också ge ett stort bidrag till en observerad kinetisk isotopeffekt och kan behöva övervägas separat, dessutom till den "halvklassiska" övergångstillståndsteorimodellen.

Deuterium kinetisk isotopeffekt ( ² H KIE) är den i särklass vanligaste, användbara och välkända typen av kinetisk isotopeffekt. Den exakta förutsägelsen av det numeriska värdet av en kinetisk isotopeffekt av deuterium med hjälp av densitetsfunktionella teoriberäkningar är nu relativt rutin. Dessutom tillåter flera kvalitativa och semikvantitativa modeller att göra grova uppskattningar av deuteriumisotopeffekter utan beräkningar, vilket ofta ger tillräckligt med information för att rationalisera experimentella data eller till och med stödja eller motbevisa olika mekanistiska möjligheter. Utgångsmaterial som innehåller deuterium är ofta kommersiellt tillgängliga, vilket gör syntesen av isotopiskt anrikade utgångsmaterial relativt enkel. Dessutom, på grund av den stora relativa skillnaden i massan av deuterium och protium och åtföljande skillnader i vibrationsfrekvenser, är storleken på isotopeffekten större än något annat par av isotoper förutom protium och tritium, vilket tillåter både primära och sekundära isotopeffekter att lätt att mäta och tolka. Däremot är sekundära effekter i allmänhet mycket små för tyngre grundämnen och nära den experimentella osäkerheten i storleksordningen, vilket komplicerar deras tolkning och begränsar deras användbarhet. I samband med isotopeffekter används väte ofta för att referera till den lätta isotopen, protium ( ¹ H), specifikt. I resten av denna artikel bör hänvisning till väte och deuterium i parallella grammatiska konstruktioner eller direkta jämförelser mellan dem tolkas som att de refererar till protium och deuterium.

Teorin om kinetiska isotopeffekter formulerades första gången av Jacob Bigeleisen 1949. Bigeleisens allmänna formel för deuteriumkinetiska isotopeffekter (som även är tillämplig på tyngre grundämnen) ges nedan. _Den använder övergångstillståndsteori och en statistisk mekanisk behandling av translations-, rotations- och vibrationsnivåer för beräkning av _{hastighetskonstanter} kH och kD . Denna formel är dock "halvklassisk" genom att den försummar bidraget från kvanttunnelering, som ofta introduceras som en separat korrigeringsfaktor. Bigeleisens formel behandlar inte heller skillnader i icke-bundna repulsiva interaktioner orsakade av den något kortare C–D-bindningen jämfört med en C–H-bindning. I ekvationen avser kvantiteter med underskriften H eller D den väte- respektive deuterium-substituerade arten, medan mängder med eller utan dubbeldolken, ‡, avser övergångstillståndet respektive reaktantgrundtillståndet. (Strängt taget bör en $\kappa _{\mathrm {H} }/\kappa _{\mathrm {D} }$ term som är ett resultat av en isotopisk skillnad i transmissionskoefficienter också inkluderas.)

${\frac {k_{{\ce {H}}}}{k_{{\ce {D}}}} }=\left({\frac {\sigma _{{\ce {H}}}\sigma _{{\ce {D}}}^{\ddagger }}{\sigma _{{\ce {D} }}\sigma _{{\ce {H}}}^{\ddagger }}}\right)\left({\frac {M_{{\ce {H}}}^{\ddagger }M_{{\ ce {D}}}}{M_{{\ce {D}}}^{\ddagger }M_{{\ce {H}}}}}\right)^{\frac {3}{2}}\ vänster({\frac {I_{x{\ce {H}}}^{\ddagger}I_{y{\ce {H}}}^{\ddagger}I_{z{\ce {H}}}^ {\ddagger }}{I_{x{\ce {D}}}^{\ddagger }I_{y{\ce {D}}}^{\ddagger }I_{z{\ce {D}}}^ {\ddagger }}}{\frac {I_{x{\ce {D}}}I_{y{\ce {D}}}I_{z{\ce {D}}}}{I_{x{\ ce {H}}}I_{y{\ce {H}}}I_{z{\ce {H}}}}}\right)^{\frac {1}{2}}\left({\frac {\prod \limits _{i=1}^{3N^{\ddagger }-7}{\frac {1-e^{-u_{i{\ce {D}}}^{\ddagger }}} {1-e^{-u_{i{\ce {H}}}^{\ddagger }}}}}{\prod \limits _{i=1}^{3N-6}{\frac {1- e^{-u_{i{\ce {D}}}}}{1-e^{-u_{i{\ce {H}}}}}}}}\right)e^{-{\frac {1}{2}}\left[\sum \limits _{i=1}^{3N^{\ddagger }-7}(u_{i{\ce {H}}}^{\ddagger }-u_ {i{\ce {D}}}^{\ddagger })-\sum \limits _{i=1}^{3N-6}(u_{i{\ce {H}}}-u_{i{ \ce {D}}})\right]}$ ,

där vi definierar

${\displaystyle u_{i}:={\frac {h\nu _{i}}{k_{\mathrm {B} } T}}={\frac {hcN_{\mathrm {A} }{\tilde {\nu }}_{i}}{RT}}} och$ u $u_{i}^{\ddagger }:={\frac {h\nu _{i}^{\ddagger }}{k_{\mathrm {B} }T} }={\frac {hcN_{\mathrm {A} }{\tilde {\nu }}_{i}^{\ddagger }}{RT}}$ .

Här är h Planck-konstanten , k _B är Boltzmann-konstanten , ${\tilde {\nu }}_{i}$ är vibrationens frekvens, uttryckt i vågtal , c är hastigheten för ljus , N _A är Avogadro-konstanten och R är den universella gaskonstanten . σ _X (X = H eller D) är symmetritalen för reaktanterna och övergångstillstånden. M _X är molekylmassorna för motsvarande arter, och termerna I _{q X} ( q = x , y , eller z ) är tröghetsmomenten kring de tre huvudaxlarna. U ( _{i X} är direkt proportionella mot motsvarande vibrationsfrekvenser, νi _. , och vibrationsnollpunktsenergin se nedan) Heltalen N och N ^‡ är antalet atomer i reaktanterna respektive övergångstillstånden. Det komplicerade uttrycket ovan kan representeras som produkten av fyra separata faktorer:

${\frac {k_{{\ce {H}}}}{k_{{\ce {D}}}}}= \mathbf {S} \times \mathbf {MMI} \times \mathbf {EXC} \times \mathbf {ZPE}$ .

För det speciella fallet med deuteriumisotopeffekter kommer vi att hävda att de tre första termerna kan behandlas som lika med eller väl approximerade av enhet. Den första faktorn S (som innehåller σ _X ) är förhållandet mellan symmetritalen för de olika arterna. Detta kommer att vara ett rationellt tal (ett förhållande mellan heltal) som beror på antalet molekylära och bindningsrotationer som leder till permutation av identiska atomer eller grupper i reaktanterna och övergångstillståndet. För system med låg symmetri kommer alla σ _X (reaktant och övergångstillstånd) att vara enhet; sålunda S ofta försummas. MMI - faktorn (innehållande M _X och I _{q X} ) hänvisar till förhållandet mellan molekylmassorna och tröghetsmomenten. Eftersom väte och deuterium tenderar att vara mycket lättare jämfört med de flesta reaktanter och övergångstillstånd, är det liten skillnad i molekylmassorna och tröghetsmomenten mellan H- och D-innehållande molekyler, så MMI-faktorn är vanligtvis också approximerad som enhet . EXC - faktorn (som innehåller produkten av vibrationsfördelningsfunktioner ) korrigerar för den kinetiska isotopeffekten som orsakas av reaktionerna hos vibrationsexciterade molekyler. Fraktionen av molekyler med tillräckligt med energi för att ha exciterade tillstånd A–H/D-bindningsvibrationer är i allmänhet liten för reaktioner vid eller nära rumstemperatur (bindningar till väte vibrerar vanligtvis vid 1000 cm −1 eller högre, så exp( ^- u i ₎ = exp(- hν _i / k _B T ) < 0,01 vid 298 K, vilket resulterar i försumbara bidrag från 1–exp(- u _i ) faktorerna). För kinetiska isotopeffekter av väte/deuterium domineras de observerade värdena vanligtvis av den sista faktorn, ZPE (en exponentiell funktion av vibrationsnollpunktsenergiskillnader), som består av bidrag från nollpunktsenergiskillnaderna för var och en av vibrationerna lägen för reaktanterna och övergångstillståndet, som kan representeras enligt följande:

${\begin{aligned}{\frac {k_{ {\ce {H}}}}{k_{{\ce {D}}}}}&\cong \exp \left\{-{\frac {1}{2}}\left[\sum \limits _ {i=1}^{3N^{\ddagger }-7}(u_{i{\ce {H}}}^{\ddagger }-u_{i{\ce {D}}}^{\ddagger } )-\sum \limits _{i=1}^{3N-6}(u_{i{\ce {H}}}-u_{i{\ce {D}}})\right]\right\} \\&\cong \exp \left[\sum _{i}^{\mathrm {(reagera.)} }{\frac {1}{2}}\Delta u_{i}-\summa _{i} ^{\mathrm {(TS)} }{\frac {1}{2}}\Delta u_{i}^{\ddagger }\right]\end{aligned}}$ ,

där vi definierar

$\Delta u_{i}:=u_{i\mathrm {H} }-u_{i\mathrm {D} }$ och $\Delta u_{i}^{\ddagger }:=u_{i\mathrm {H} }^{\ddagger }-u_{i\mathrm {D} }^ {\dagger }$ .

Summorna i exponenten för det andra uttrycket kan tolkas som att de löper över alla vibrationslägen för reaktantgrundtillståndet och övergångstillståndet. Alternativt kan man tolka dem som att de löper över de moder som är unika för reaktanten eller övergångstillståndet eller vars vibrationsfrekvenser ändras väsentligt vid avancemang längs reaktionskoordinaten. De återstående paren av reaktant- och övergångstillståndsvibrationslägen har mycket likartade $\Delta u_{i}$ och ${\displaystyle \Delta u_{i}^{\ddagger }} ,$ och annulleringar inträffar när summorna i exponenten beräknas. I _{praktiken är} deuterium-KIEs därför ofta till stor del beroende av en handfull nyckelvibrationslägen på grund av denna avstängning, vilket gör kvalitativa analyser av kH / kD möjliga.

Som nämnts, speciellt för väte/deuterium-substitution, uppstår de flesta kinetiska isotopeffekter från skillnaden i nollpunktsenergi (ZPE) mellan reaktanterna och övergångstillståndet för de aktuella isotopologerna, och denna skillnad kan förstås kvalitativt med följande beskrivning : inom Born–Oppenheimer-approximationen är den potentiella energiytan densamma för båda isotoparterna. En kvantmekanisk behandling av energin introducerar dock diskreta vibrationsnivåer på denna kurva, och lägsta möjliga energitillstånd för en molekyl motsvarar den lägsta vibrationsenerginivån, som är något högre i energi än minimum av den potentiella energikurvan. Denna skillnad, som kallas nollpunktsenergin, är en manifestation av Heisenbergs osäkerhetsprincip som kräver en osäkerhet i CH- eller CD-bindningslängden. Eftersom den tyngre (i det här fallet den deutererade) arten beter sig mer "klassiskt" är dess vibrationsenerginivåer närmare den klassiska potentiella energikurvan, och den har en lägre nollpunktsenergi. Nollpunktsenergiskillnaderna mellan de två isotopiska arterna, åtminstone i de flesta fall, minskar i övergångstillståndet, eftersom bindningskraftskonstanten minskar under bindningsbrott. Följaktligen översätts den lägre nollpunktsenergin för den deutererade arten till en större aktiveringsenergi för dess reaktion, som visas i följande figur, vilket leder till en normal kinetisk isotopeffekt. Denna effekt bör i princip tas med i beräkningen alla 3 N− 6 vibrationslägen för utgångsmaterialet och 3 N ^‡ − 7 vibrationslägen vid övergångstillståndet (ett läge, det som motsvarar reaktionskoordinaten, saknas vid övergångstillstånd, eftersom en bindning bryts och det inte finns någon återställande kraft mot rörelsen). Den harmoniska oscillatorn är en bra approximation för en vibrerande bindning, åtminstone för lågenergi vibrationstillstånd. Kvantmekaniken ger vibrationsnollpunktsenergin som $\epsilon _{i}^{(0)}={\frac {1}{2}}h\nu _ {i}$ . Således kan vi enkelt tolka faktorn ½ och summan av $u_{i}=h\nu _{i}/k_{\mathrm {B} }T$ termer över marktillstånd och övergångstillstånd vibrationslägen i exponenten av den förenklade formeln ovan. För en harmonisk oscillator är vibrationsfrekvensen omvänt proportionell mot kvadratroten av det vibrerande systemets reducerade massa:

$\nu _{\mathrm {X} }={\frac {1}{2\pi }}{\sqrt {\frac {k_{\mathrm {f} }}{\mu _{\mathrm {X} }}}}\cong {\frac {1}{2\pi }}{\sqrt {\frac {k_{\mathrm { f} }}{m_{\mathrm {X} }}}}$ ,

där k _f är kraftkonstanten . Dessutom är den reducerade massan approximerad av massan av den lätta atomen i systemet, X = H eller D. Eftersom m _D är ungefär 2 m _H ,

$\Delta u_{i}\cong \left(1-{\frac {1}{\sqrt {2}}}\right) {\frac {h\nu _{i\mathrm {H} }}{k_{\mathrm {B} }T}}$ .

I fallet med en homolytisk C–H/D-bindningsdissociation försvinner övergångstillståndstermen, och om man försummar andra vibrationsmoder, k _H / k _D = exp(½Δ u _i ). Således observeras en större isotopeffekt för en styvare ("starkare") C–H/D-bindning. För de flesta reaktioner av intresse överförs en väteatom mellan två atomer, med ett övergångstillstånd [A···H···B] ‡ ^och vibrationslägen vid övergångstillståndet måste beaktas. Ändå är det fortfarande allmänt sant att klyvning av en bindning med högre vibrationsfrekvens ger en större isotopeffekt.

ZPE-energiskillnader och motsvarande skillnader i aktiveringsenergierna för brytning av analoga CH- och CD-bindningar. Observera att i detta schematiska diagram representerar kurvorna faktiskt (3 N- 6)- och (3 N ^‡ -7)-dimensionella hyperytor, och att vibrationsläget vars ZPE illustreras i övergångstillståndet inte är detsamma som reaktionskoordinat. Reaktionskoordinaten representerar en vibration med en negativ kraftkonstant (och imaginär vibrationsfrekvens) för övergångstillståndet. Den ZPE som visas för marktillståndet kan hänvisa till vibrationen som motsvarar reaktionskoordinaten i fallet med en primär KIE.

För att beräkna det maximala möjliga värdet för en icke-tunnelerande deuterium KIE, betraktar vi fallet där nollpunktsenergiskillnaden mellan sträckningsvibrationerna för en typisk kol-vätebindning (3000 cm −1) ^och kol-deuteriumbindning (2200) cm ⁻¹ ) försvinner i övergångstillståndet (en energiskillnad på (1/2)(3000 – 2200 cm ⁻¹ ) = 400 cm ⁻¹ , eller ca 1,15 kcal/mol), utan någon kompensation från en nollpunktsenergi skillnad i övergångstillståndet (t.ex. från den symmetriska A···H···B-sträckningen, som är unik för övergångstillståndet). Den förenklade formeln ovan förutsäger ett maximum för k _H / k _D som 6,9. Om det fullständiga försvinnandet av två böjningsvibrationer också ingår, k _H / k _D -värden så stora som 15-20 förutsägas. Det är _dock mycket osannolikt att böjningsfrekvenser försvinner i övergångstillståndet, och det finns bara ett fåtal fall där _kH/kD - värden överstiger 7-8 nära rumstemperatur. Dessutom upptäcks det ofta att tunnling är en viktig faktor när de överskrider sådana värden. Ett värde på k _H / k _D ~ 10 tros vara maximalt för en semi-klassisk primär kinetisk isotopeffekt (ingen tunnling) för reaktioner som äger rum runt 298 K. (Formeln för k H / k _D har ett _{temperaturberoende} , så större isotopeffekter är möjliga vid lägre temperaturer). Beroende på typen av övergångstillstånd för H-överföring (symmetrisk vs. "tidig" eller "sen" och linjär vs. böjd), varierar i vilken utsträckning en primär deuteriumisotopeffekt närmar sig detta maximum. En modell utvecklad av Westheimer förutspådde att symmetriska (termoneutrala, av Hammond Postulate ), linjära övergångstillstånd har de största isotopeffekterna, medan övergångstillstånd som är "tidiga" eller "sena" (för exoterma respektive endotermiska reaktioner), eller olinjära (t.ex. cykliska) uppvisar mindre effekter. Dessa förutsägelser har sedan dess fått omfattande experimentellt stöd.

För sekundära deuteriumisotopeffekter föreslog Streitwieser att försvagning (eller förstärkning, i fallet med en omvänd isotopeffekt) av böjningslägen från reaktantgrundtillståndet till övergångstillståndet är till stor del ansvarig för observerade isotopeffekter. Dessa förändringar tillskrivs en förändring i sterisk miljö när kolet bundet till H/D genomgår rehybridisering från sp ³ till sp ² eller vice versa (en α sekundär kinetisk isotopeffekt), eller bindningsförsvagning på grund av hyperkonjugering i fall där en karbokatisering genereras en kolatom bort (en β sekundär kinetisk isotopeffekt). Dessa isotopeffekter har ett teoretiskt maximum på k _H / k _D = 2 ^0,5 ≈ 1,4. För en sekundär kinetisk isotopeffekt vid α-positionen ger rehybridisering från sp ³ till sp ² en normal isotopeffekt, medan rehybridisering från sp ² till sp ³ resulterar i en omvänd isotopeffekt med ett teoretiskt minimum av k _H / k _D = 2 ^-0,5 ≈ 0,7. I praktiken k _H / k _D ~ 1,1-1,2 och k _H / k _D ~ 0,8-0,9 typiska för α sekundära kinetiska isotopeffekter, medan k _H / k _D ~ 1,15-1,3 är typiska för β sekundär kinetisk isotopeffekt. För reaktanter som innehåller flera isotopiskt substituerade β-väteatomer är den observerade isotopeffekten ofta resultatet av att flera H/D:er vid β-positionen verkar i samverkan. I dessa fall är effekten av varje isotopiskt märkt atom multiplikativ, och fall där k _H / k _D > 2 är inte ovanliga.

Följande enkla uttryck som relaterar deuterium- och tritium-kinetiska isotopeffekter, som också är kända som Swain-ekvationen (eller Swain-Schaad-Stivers ekvationer), kan härledas från det allmänna uttrycket ovan med några förenklingar:

$\left({\frac {\ln \left({\frac {k_{{\ce {H}}}}{k_{{\ce {T}}}}}\höger)}{\ln \left( {\frac {k_{{\ce {H}}}}{k_{{\ce {D}}}}}\right)}}\right)_{s}\cong {\frac {1-{\ sqrt {m_{{\ce {H}}}/m_{{\ce {T}}}}}}{1-{\sqrt {m_{{\ce {H}}}/m_{{\ce { D}}}}}}}={\frac {1-{\sqrt {1/3}}}{1-{\sqrt {1/2}}}}\cong 1.44$ ;

dvs.

$\left({\frac {k_{{\ce {H}}}}{k_{{\ce {T}}}}} \right)_{s}=\left({\frac {k_{{\ce {H}}}}{k_{{\ce {D}}}}}\right)_{s}^{1.44}$ .

För att härleda dessa uttryck användes den rimliga approximationen att reducerade massor är ungefär lika med massorna av väte, deuterium eller tritium. Dessutom antogs vibrationsrörelsen approximeras av en harmonisk oscillator, så att $u_{i\mathrm {X} }\propto \ mu _{\mathrm {X} }^{-1/2}\cong m_{\mathrm {X} }^{-1/2}$ (X = H, D eller T). Underskriften " s " hänvisar till dessa "halvklassiska" kinetiska isotopeffekter, som bortser från kvanttunnling. Tunnelbidrag måste behandlas separat som en korrektionsfaktor.

För isotopeffekter som involverar andra element än väte är många av dessa förenklingar inte giltiga, och omfattningen av isotopeffekten kan starkt bero på några eller alla de försummade faktorerna. Således är kinetiska isotopeffekter för andra grundämnen än väte ofta mycket svårare att rationalisera eller tolka. I många fall och särskilt för väteöverföringsreaktioner är bidragen till kinetiska isotopeffekter från tunneldrivning betydande (se nedan).

Tunneldrivning

I vissa fall ses en ytterligare hastighetsökning för den lättare isotopen, möjligen på grund av kvantmekanisk tunnling . Detta observeras vanligtvis endast för reaktioner som involverar bindningar till väteatomer. Tunnling uppstår när en molekyl penetrerar genom en potentiell energibarriär snarare än över den. Även om det inte är tillåtet av den klassiska mekanikens lagar , kan partiklar passera genom klassiskt förbjudna områden i rymden i kvantmekaniken baserad på våg-partikeldualitet .

Den potentiella energikällan för en tunnelreaktion. Den streck-röda pilen visar den klassiskt aktiverade processen, medan den helröda pilen visar tunnelbanan.

Analys av tunnling kan göras med hjälp av Bells modifiering av Arrhenius-ekvationen , som inkluderar tillägget av en tunnlingsfaktor, Q:

$k=QAe^{-E/RT}$

där A är Arrhenius-parametern, E är barriärhöjden och

$Q={\frac {e^{\alpha }}{\beta -\alpha }}(\beta e^{-\ alfa }-\alpha e^{-\beta })$

där $\alpha ={\frac {E}{RT}}$ och $\beta ={\frac {2a \pi ^{2}(2mE)^{1/2}}{h}}$

Undersökning av β -termen visar exponentiellt beroende av partikelns massa. Som ett resultat är tunnling mycket mer sannolikt för en lättare partikel som väte. Att helt enkelt fördubbla massan av en tunnelproton genom att ersätta den med dess deuteriumisotop minskar drastiskt hastigheten för sådana reaktioner. Som ett resultat observeras mycket stora kinetiska isotopeffekter som inte kan förklaras av skillnader i nollpunktsenergier.

Donator-Acceptor Modell av en protonöverföring.

Dessutom beror β -termen linjärt med barriärens bredd, 2a. Precis som med massa är tunnling störst för små barriärbredder. Optimala tunnelavstånd för protoner mellan donator- och acceptoratom är 0,4 Å.

Temperaturberoende vid tunneldrivning

Tunneling är en kvantmekanisk effekt knuten till vågmekanikens lagar, inte kinetiken . Därför tenderar tunnling att bli viktigare vid låga temperaturer, där även de minsta kinetiska energibarriärerna kanske inte kan övervinnas utan kan tunnlas igenom.

Peter S. Zuev et al. rapporterade hastighetskonstanter för ringexpansionen av 1-metylcyklobutylfluorkarben till 4,0 x 10 ⁻⁶ /s i kväve och 4,0 x 10 ⁻⁵ /s i argon vid 8 kelvin. De beräknade att vid 8 kelvin skulle reaktionen fortgå via ett enda kvanttillstånd av reaktanten så att den rapporterade hastighetskonstanten är temperaturoberoende och tunnlingsbidraget till hastigheten var 152 storleksordningar större än bidraget från passage över övergångstillståndet energibarriär.

Så trots det faktum att konventionella kemiska reaktioner tenderar att sakta ner dramatiskt när temperaturen sänks, förändras tunnelreaktioner sällan alls. Partiklar som tunnlar genom en aktiveringsbarriär är ett direkt resultat av det faktum att vågfunktionen hos en mellanliggande art, reaktant eller produkt inte är begränsad till energikällan i ett visst tråg längs energiytan av en reaktion utan kan "läcka ut" till nästa energiminimum. Mot bakgrund av detta bör tunnling vara temperaturoberoende.

_över temperaturintervallet 363–463 K, karakteriserades H/D kinetiska isotopeffektdata av små preexponentiella faktorförhållanden A _H / AD från 0,43 till 0,54 och stora aktiveringsenergiskillnader från 9,0 till 9,7 kJ/mol. Baserat på sina argument på övergångstillståndsteori gav de små A- faktorförhållandena förknippade med de stora skillnaderna i aktiveringsenergi (vanligtvis cirka 4,5 kJ/mol för C–H(D)-bindningar) starka bevis för tunnelbildning. För syftet med denna diskussion är det viktigt att A- faktorförhållandet för de olika paraffinerna de använde var ungefär konstant över hela temperaturområdet.

Observationen att tunnling inte är helt temperaturoberoende kan förklaras av det faktum att inte alla molekyler av en viss art upptar sitt vibrationsgrundtillstånd vid varierande temperaturer. Att lägga till termisk energi till en potentiell energikälla kan orsaka att högre vibrationsnivåer andra än grundtillståndet blir befolkade. För en konventionell kinetiskt driven reaktion skulle denna excitation endast ha en liten inverkan på hastigheten. Men för en tunnelreaktion kan skillnaden mellan nollpunktsenergin och den första vibrationsenerginivån vara enorm. Tunnelkorrigeringstermen Q är linjärt beroende av barriärens bredd och denna bredd minskas avsevärt när antalet vibrationslägen på Morsepotentialen ökar. Minskningen av barriärens bredd kan ha en så stor inverkan på tunneldrivningshastigheten att även en liten population av exciterade vibrationstillstånd skulle dominera denna process.

Kriterier för KIE-tunnling

För att avgöra om tunnling är involverad i KIE av en reaktion med H eller D, övervägs några kriterier:

1. Δ( E _a ^H - E _a ^D Ea ₎ > Δ( ZPE ^H - ZPE ^D ) ( =aktiveringsenergi; ZPE=nollpunktsenergi)
2. Reaktionen fortsätter fortfarande vid lägre temperaturer.
3. Arrhenius preexponentiella faktorer A _D / A _H är inte lika med 1 .
4. En stor negativ aktiveringsentropi .
5. Reaktanternas och produkternas geometri är vanligtvis mycket lika.

Också för reaktioner där isotoper inkluderar H, D och T, är ett kriterium för tunnling Swain-Schaad-relationerna som jämför hastighetskonstanterna ( k ) för reaktionerna där H, D eller T byts ut:

k _H / k _T =( k _D / k _T ) ^X och k _H / k _T =( k _H / k _D ) ^Y

Experimentella värden på X som överstiger 3,26 och Y lägre än 1,44 är bevis på ett visst bidrag från tunneldrivning .

Exempel på tunnling i KIE

I organiska reaktioner har denna protontunneleffekt observerats i sådana reaktioner som deprotonering och jodering av nitropropan med hindrad pyridinbas med en rapporterad KIE på 25 vid 25 °C:

och i ett 1,5-sigmatropiskt väteskifte även om det observeras att det är svårt att extrapolera experimentella värden som erhållits vid förhöjda temperaturer till lägre temperaturer:

Det har länge spekulerats i att hög effektivitet av enzymkatalys i proton- eller hydridjonöverföringsreaktioner delvis kan bero på den kvantmekaniska tunneleffekten. Miljön vid den aktiva platsen för ett enzym placerar donator- och acceptoratomen nära det optimala tunnelavståndet, där aminosyrasidokedjorna kan "tvinga" donator- och acceptoratomen närmare varandra genom elektrostatiska och icke-kovalenta interaktioner. Det är också möjligt att enzymet och dess ovanliga hydrofoba miljö inuti en reaktionsplats ger tunnelfrämjande vibrationer. Studier på ketosteroidisomeras har gett experimentella bevis för att enzymet faktiskt förbättrar den kopplade rörelsen/väte-tunnlingen genom att jämföra primära och sekundära kinetiska isotopeffekter av reaktionen under enzymkatalyserade och icke-enzymkatalyserade förhållanden.

Det finns många exempel på protontunnling i enzymkatalyserade reaktioner som upptäcktes av KIE. Ett väl studerat exempel är metylamindehydrogenas, där stora primära KIE på 5–55 har observerats för protonöverföringssteget.

Mekanism av metylamindehydrogenas, kinoproteinet omvandlar primära aminer till aldehyd och ammoniak.

Ett annat exempel på tunnlingsbidrag till protonöverföring i enzymatiska reaktioner är reaktionen som utförs av alkoholdehydrogenas . Konkurrenskraftiga KIE:er för väteöverföringssteget vid 25 °C resulterade i 3,6 och 10,2 för primära respektive sekundära KIE:er.

Mekanism av alkoholdehydrogenas. Det hastighetsbegränsande steget är protonöverföringen

Övergående kinetisk isotopeffekt

Huvudartikel: Transient kinetisk isotopfraktionering

Isotopeffekt uttryckt med ekvationerna ovan hänvisar endast till reaktioner som kan beskrivas med första ordningens kinetik . I alla fall där detta inte är möjligt övergående kinetiska isotopeffekter beaktas med GEBIK- och GEBIF-ekvationerna.

Experiment

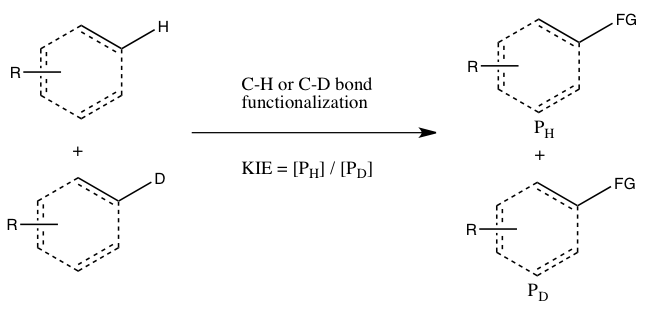
Simmons och Hartwig hänvisar till följande tre fall som huvudtyperna av kinetiska isotopeffektexperiment som involverar CH-bindningsfunktionalisering:

A) KIE bestämt från absoluta hastigheter av två parallella reaktioner

I detta experiment bestäms hastighetskonstanterna för det normala substratet och dess isotopiskt märkta analog oberoende, och KIE erhålls som ett förhållande mellan de två. Noggrannheten hos den uppmätta KIE är starkt begränsad av den noggrannhet med vilken var och en av dessa hastighetskonstanter kan mätas. Dessutom kan det vara mycket utmanande att återskapa de exakta förhållandena i de två parallella reaktionerna. Icke desto mindre indikerar en mätning av en stor kinetisk isotopeffekt genom direkt jämförelse av hastighetskonstanter att CH-bindningsklyvning sker vid det hastighetsbestämmande steget. (Ett mindre värde kan indikera en isotopeffekt på grund av en förjämvikt, så att CH-bindningsklyvningen sker någonstans före det hastighetsbestämmande steget.)

B) KIE bestämd från en intermolekylär tävling

I denna typ av experiment används samma substrat som används i Experiment A, men de släpps in för att reagera i samma behållare, istället för två separata behållare. Den kinetiska isotopeffekten från detta experiment bestäms av den relativa mängden produkter som bildas från CH kontra CD-funktionalisering (eller så kan den härledas från de relativa mängderna av oreagerade utgångsmaterial). Det är nödvändigt att släcka reaktionen innan den slutförs för att observera den kinetiska isotopeffekten (se avsnittet Utvärdering nedan). I allmänhet stoppas reaktionen vid låg omvandling (~5 till 10 % omvandling) eller ett stort överskott (> 5 ekv.) av isotopblandningen används. Denna experimenttyp säkerställer att både CH- och CD-bindningsfunktionaliseringar sker under exakt samma förhållanden, och förhållandet mellan produkter från CH- och CD-bindningsfunktionaliseringar kan mätas med mycket större precision än hastighetskonstanterna i Experiment A. Dessutom, endast en enda mätning av produktkoncentrationer från ett enda prov krävs. Emellertid är en observerad kinetisk isotopeffekt från detta experiment svårare att tolka, eftersom det antingen kan innebära att CH-bindningsklyvning sker under det hastighetsbestämmande steget eller vid ett produktbestämmande steg som följer på det hastighetsbestämmande steget. Frånvaron av en kinetisk isotopeffekt, åtminstone enligt Simmons och Hartwig, är inte desto mindre en indikation på att CH-bindningsklyvningen inte inträffar under det hastighetsbestämmande steget.

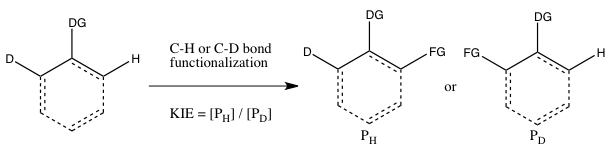
C) KIE bestämd från en intramolekylär konkurrens

Denna typ av experiment är analog med experiment B, förutom att det denna gång finns en intramolekylär konkurrens för CH- eller CD-bindningens funktionalisering. I de flesta fall har substratet en styrgrupp (DG) mellan CH- och CD-bindningarna. dess tolkning följer samma överväganden som i Experiment B. Resultaten av Experiment B och C kommer dock att skilja sig om den irreversibla bindningen av det isotopinnehållande substratet äger rum i Experiment B före klyvningen av CH- eller CD-bindningen. I ett sådant scenario kan en isotopeffekt observeras i Experiment C (där valet av isotopen kan ske även efter substratbindning) men inte i Experiment B (eftersom valet av om CH- eller CD-bindningen klyvs redan är gjort så snart som substratet binder irreversibelt). Till skillnad från experiment B behöver reaktionen inte stoppas vid låg förbrukning av isotopiskt utgångsmaterial för att erhålla en exakt kH / kD , _eftersom förhållandet mellan H och D i utgångsmaterialet är 1:1, _oavsett omvandlingens omfattning.

Ett icke-CH-aktiveringsexempel på olika isotopeffekter som observeras i fallet med intermolekylär (Experiment B) och intramolekylär (Experiment C) konkurrens är fotolysen av difenyldiazometan i närvaro av t -butylamin. För att förklara detta resultat föreslogs bildandet av difenylkarben, följt av irreversibel nukleofil attack av t -butylamin. Eftersom det är liten isotopskillnad i hastigheten för nukleofila attacker resulterade det intermolekylära experimentet i en KIE nära 1. I det intramolekylära fallet bestäms dock produktförhållandet av protonöverföringen som sker efter den nukleofila attacken, en process för som det finns en betydande KIE på 2,6.

Experiment A, B och C kommer alltså att ge resultat med olika precisionsnivåer och kräver olika experimentell uppsättning och olika sätt att analysera data. Som ett resultat kommer genomförbarheten av varje typ av experiment att bero på reaktionens kinetiska och stökiometriska profil, såväl som reaktionsblandningens fysikaliska egenskaper (t.ex. homogen vs. heterogen). Dessutom, som noterats i stycket ovan, tillhandahåller experimenten kinetisk isotopeffektdata för olika steg i en flerstegsreaktion, beroende på de relativa platserna för det hastighetsbegränsande steget, produktbestämmande steg och/eller CH/D-klyvning steg.

De hypotetiska exemplen nedan illustrerar vanliga scenarier. Betrakta följande reaktionskoordinatdiagram. För en reaktion med denna profil kommer alla tre experimenten (A, B och C) att ge en signifikant primär kinetisk isotopeffekt:

Reaktionsenergiprofil för när CH-klyvning sker vid RDS

Å andra sidan, om en reaktion följer följande energiprofil, där CH- eller CD-bindningsklyvningen är irreversibel men sker efter det hastighetsbestämmande steget (RDS), kommer ingen signifikant kinetisk isotopeffekt att observeras med experiment A, eftersom den totala hastigheten påverkas inte av den isotopiska substitutionen. Icke desto mindre kommer det irreversibla CH-bindningsspjälkningssteget att ge en primär kinetisk isotopeffekt med de andra två experimenten, eftersom det andra steget fortfarande skulle påverka produktfördelningen. Därför är det med experiment B och C möjligt att observera den kinetiska isotopeffekten även om CH- eller CD-bindningsklyvning inte sker i det hastighetsbestämmande steget, utan i det produktbestämmande steget.

Reaktionsenergiprofil för när CH-bindningsklyvningen sker vid ett produktbestämmande steg efter RDS

Utvärdering av kinetiska isotopeffekter i en hypotetisk flerstegsreaktion

En stor del av den kinetiska isotopeffekten härrör från vibrationsnollpunktsenergiskillnader mellan reaktantens grundtillstånd och övergångstillståndet som varierar mellan reaktanten och dess isotopiskt substituerade analog. Även om det är möjligt att utföra involverade beräkningar av kinetiska isotopeffekter med hjälp av beräkningskemi, är mycket av det utförda arbetet av enklare ordning som involverar undersökning av huruvida särskilda isotopsubstitutioner ger en detekterbar kinetisk isotopeffekt eller inte. Vibrationsförändringar från isotopsubstitution vid atomer bort från platsen där reaktionen inträffar tenderar att avbryta mellan reaktanten och övergångstillståndet. Därför indikerar närvaron av en kinetisk isotopeffekt att den isotopiskt märkta atomen är vid eller mycket nära reaktionsstället.

Frånvaron av en isotopeffekt är svårare att tolka: Det kan betyda att den isotopiskt märkta atomen är borta från reaktionsstället, men det kan också innebära att det finns vissa kompenserande effekter som leder till avsaknaden av en observerbar kinetisk isotopeffekt. Till exempel kan skillnaderna mellan reaktanten och övergångstillståndets nollpunktsenergier vara identiska mellan den normala reaktanten och dess isotopiskt märkta version. Alternativt kan det betyda att den isotopiska substitutionen är vid reaktionsstället, men vibrationsförändringar associerade med bindningar till denna atom inträffar efter det hastighetsbestämmande steget. Ett sådant fall illustreras i följande exempel, där ABCD representerar en molekyls atomskelett.

Om man antar stationära förhållanden för mellanliggande ABC, är den totala reaktionshastigheten följande:

${\frac {d[A]}{dt}}={\frac {k_{1} k_{3}[ABCD]}{k_{2}[D]+k_{3}}}$

Om det första steget är hastighetsbestämmande, reduceras denna ekvation till:

${\frac {d[A]}{dt}}=k_{1}[ABCD]$

Eller om det andra steget är hastighetsbestämmande, reduceras ekvationen till:

${\frac {d[A]}{dt}}={\frac {k_{1}k_{3 [ABCD]}{k_{2}[D]}}$

I de flesta fall kommer isotopsubstitution vid A, speciellt om det är en tung atom, inte att förändra k ₁ eller k ₂ , men det kommer med största sannolikhet att ändra k ₃ . Därför, om det första steget är hastighetsbestämmande, kommer det inte att finnas en observerbar kinetisk isotopeffekt i den totala reaktionen med isotopmärkning av A, men det kommer att finnas en om det andra steget är hastighetsbestämmande. För mellanliggande fall där båda stegen har jämförbara hastigheter kommer storleken på den kinetiska isotopeffekten att bero på förhållandet k ₃ och k ₂ .

Isotopisk substitution av D kommer att förändra k ₁ och k ₂ utan att påverka k ₃ . Den kinetiska isotopeffekten kommer alltid att vara observerbar med denna substitution eftersom k ₁ förekommer i det förenklade hastighetsuttrycket oavsett vilket steg som är hastighetsbestämmande, men det kommer att vara mindre uttalat om det andra steget är hastighetsbestämmande på grund av viss utsläckning mellan isotopen effekter på k ₁ och k ₂ . Detta utfall är relaterat till det faktum att jämviktsisotopeffekter vanligtvis är mindre än kinetiska isotopeffekter.

Isotopisk substitution av B kommer klart att förändra k ₃ , men det kan också ändra k ₁ i mindre utsträckning om BC-bindningsvibrationerna påverkas i övergångstillståndet i det första steget. Det kan alltså bli en liten isotopeffekt även om det första steget är hastighetsbestämmande.

Detta hypotetiska övervägande avslöjar hur observation av kinetiska isotopeffekter kan användas för att undersöka reaktionsmekanismer. Förekomsten av en kinetisk isotopeffekt indikerar en förändring av vibrationskraftkonstanten för en bindning associerad med den isotopiskt märkta atomen vid eller före det hastighetskontrollerande steget. Intrikata beräkningar kan användas för att lära sig mycket detaljer om övergångstillståndet från observerade kinetiska isotopeffekter. Vanligare är dock att bara den kvalitativa kunskapen att en bindning associerad med den isotopiskt märkta atomen förändras på ett visst sätt kan vara mycket användbar.

Utvärdering av hastighetskonstantkvoter från intermolekylära konkurrensreaktioner

I konkurrensreaktioner beräknas den kinetiska isotopeffekten från isotopprodukt eller kvarvarande reaktantförhållanden efter reaktionen, men dessa förhållanden beror starkt på graden av fullbordande av reaktionen. Vanligtvis kommer det isotopiska substratet att bestå av molekyler märkta i en specifik position och deras omärkta, vanliga motsvarigheter. Det är också möjligt vid ^13C kinetiska isotopeffekter, såväl som liknande fall, att helt enkelt förlita sig på den naturliga mängden av isotopkolet för experimenten med kinetisk isotopeffekt, vilket eliminerar behovet av isotopmärkning. De två isotopiska substraten kommer att reagera genom samma mekanism, men med olika hastigheter. Förhållandet mellan mängderna av de två arterna i reaktanterna och produkterna kommer således att förändras gradvis under reaktionens gång, och denna gradvisa förändring kan behandlas på följande sätt: Antag att två isotopiska molekyler, A 1 _och A ₂ , genomgå irreversibla konkurrensreaktioner på följande sätt:

${\begin{aligned}{\ce {{A1}+{B}+{C} +\cdots }}\ &{\ce {->[k_{1}]P1}}\\{\ce {{A2}+{B}+{C}+\cdots }}\ &{\ce { ->[k_{2}]P2}}\end{aligned}}$

Den kinetiska isotopeffekten för detta scenario visar sig vara:

${\text{KIE}}={k_{1} \over k_{2}}={\frac {\ln(1-F_{1})}{\ln(1-F_{2})}}$

Där F ₁ och F ₂ hänvisar till fraktionen av omvandlingar för de isotopiska arterna _Ai respektive A2 _.

Utvärdering

I denna behandling antas alla andra reaktanter vara icke-isotopa. Om man vidare antar att reaktionen är av första ordningen med avseende på det isotopiska substratet A, kan följande allmänna hastighetsuttryck för båda dessa reaktioner skrivas:

${\text{rate}}={- d[{\ce {A}}_{n}] \over dt}=k_{n}\ gånger [{\ce {A}}_{n}]\ gånger f([{\ce {B}} ],[{\ce {C}}],\cdots ){\text{ där }}n=1{\text{ eller }}2$

Eftersom f([B],[C],...) inte beror på den isotopiska sammansättningen av A, kan det lösas i båda hastighetsuttrycken med A 1 och A 2 , _och de _två kan likställas för att härleda följande relationer :

${1 \över k_{1}}\ gånger {\ce {{\mathit {d }}[A1] \över [A1]}}={1 \över k_{2}}\ gånger {\ce {{\mathit {d}}[A2] \över [A2]}}$

${1 \over k_{1}}\times \int \limits _{\ce {[A1]^{0}}}^{\ce {[A1]}}{d[{\ce {A}}'_{ 1}] \over [{\ce {A}}'_{1}]}={1 \over k_{2}}\times \int \limits _{\ce {[A2]^{0}}} ^{\ce {[A2]}}{d[{\ce {A}}'_{2}] \över [{\ce {A}}'_{2}]}$

⁰⁰ Där [Ai _] och [ _A2 ] är _de initiala koncentrationerna av Ai _respektive A2 . Detta leder till följande kinetiska isotopeffektuttryck:

${k_{1} \over k_{2}}={\frac {\ce {\ln([A1]/[A1]^{0})}}{\ce {\ln([A2]/[A2]^{0})}}}$

⁰ Vilket också kan uttryckas i form av fraktionsmängder av omvandling av de två reaktionerna, F ₁ och F ₂ , där 1-F _n =[A _n ]/[A _n ] för n = 1 eller 2, enligt följande:

${k_{1} \over k_{2}}={\frac {\ln(1-F_{1} )}{\ln(1-F_{2})}}$

Förhållandet mellan omvandlingsfraktionerna för de två konkurrerande reaktionerna med isotopiska substrat. Hastighetskonstantförhållandet k ₁ / k ₂ (KIE) varieras för varje kurva.

⁰⁰₀⁰⁰⁰⁰⁰₀ När det gäller att erhålla de kinetiska isotopeffekterna kan blandningar av substrat som innehåller stabila isotoper analyseras med hjälp av en masspektrometer, som ger förhållandena mellan de isotopiska molekylerna i det initiala substratet (definierat här som [A 2 ] / _[ A 1 _] = R ) i substratet efter viss omvandling ([A2 _] /[Ai _] =R), eller i produkten ([P2 _] /[Pi _] = _RP ). När en av arterna, t.ex. 2, är en radioaktiv isotop, kan dess blandning med den andra arten också analyseras genom dess radioaktivitet, som mäts i molära aktiviteter som är proportionella mot [A 2 ] / ( _[ A 1 _] + [ A2 ] ) ≈ [A2 _] / [Ai _] = R i det initiala substratet, [A2 _{] /} ([A1 _] +[A2 _] ) ≈ [A2 _] /[A1 _] = Rin substratet efter viss omvandling, och [R ₂ ] / ([R ₁ ]+[R ₂ ]) ≈ [R ₂ ]/[R ₁ ] = R _P , så att samma förhållanden som i det andra fallet kan mätas så länge som den radioaktiva isotopen finns i spårämnesmängder. Sådana förhållanden kan också bestämmas med användning av NMR-spektroskopi.

₀ När substratsammansättningen följs kan följande kinetiska isotopeffektuttryck i termer av R och R härledas:

${\text{KIE}}={\frac {k_{1}}{k_ {2}}}={\frac {\ln(1-F_{1})}{\ln[(1-F_{1})R/R_{0}]}}$

Mätning av Fi _i termer av vikter per volymenhet eller molariteter av reaktanterna

₀ Om man tar förhållandet mellan R och R med det tidigare härledda uttrycket för F ₂ , får man:

₀₀₀

${R \over R_{0}}={\ce {{\frac {[A2]/[A1]}{[A2]^0 /[A1]^0}}}}={\ce {{\frac {[A2]/[A2]^0}{[A1]/[A1]^0}}}}={\frac {1- F_{2}}{1-F_{1}}}=(1-F_{1})^{(k_{2}/k_{1})-1}$

Denna relation kan lösas i termer av kinetiken isotopeffekt för att erhålla KIE-uttrycket som ges ovan. När den ovanliga isotopen har mycket låg förekomst är både R och R mycket små och inte signifikant olika varandra, så att 1- F ₁ kan approximeras med m / m eller c / c .

₀ Isotopberikning av utgångsmaterialet kan beräknas från beroendet av R/R på F ₁ för olika kinetiska isotopeffekter, vilket ger följande figur. På grund av det exponentiella beroendet leder även mycket låga kinetiska isotopeffekter till stora förändringar i isotopsammansättningen av utgångsmaterialet vid höga omvandlingar.

Den isotopiska anrikningen av den relativa mängden av art 2 med avseende på art 1 i utgångsmaterialet som en funktion av omvandling av art 1. Värdet på den kinetiska isotopeffekten (k 1 / k 2 ) _anges vid varje _kurva .

₀ När produkterna följs kan den kinetiska isotopeffekten beräknas med hjälp av produktförhållandet R _P tillsammans med R enligt följande:

${k_{1} \over k_{2}}={\frac {\ln( 1-F_{1})}{\ln[1-(F_{1}R_{P}/R_{0})]}}$

Kinetisk isotopeffektmätning vid naturlig överflöd

Kinetisk isotopeffektmätning vid naturlig överflöd är en enkel generell metod för att mäta kinetiska isotopeffekter (KIE) för kemiska reaktioner utförda med material av naturlig överflöd . Denna teknik för att mäta KIE:er övervinner många begränsningar hos tidigare KIE-mätmetoder. KIE-mätningar från isotopiskt märkta material kräver en ny syntes för varje isotopiskt märkt material (en process som ofta är oöverkomligt svår), en konkurrensreaktion och en analys. KIE-mätningen vid naturlig överflöd undviker dessa problem genom att dra fördel av kvantitativa tekniker med hög precision ( kärnmagnetisk resonansspektroskopi , isotopförhållande masspektrometri ) för att selektivt mäta kinetisk fraktionering av isotoper , i antingen produkt eller utgångsmaterial för en given kemisk reaktion .

Enkelpuls NMR

Kvantitativ enkelpuls kärnmagnetisk resonansspektroskopi (NMR) är en metod som är tillgänglig för att mäta kinetisk fraktionering av isotoper för naturliga överflöd KIE-mätningar. Pascal et al. inspirerades av studier som visar dramatiska variationer av deuterium inom identiska föreningar från olika källor och antog att NMR kunde användas för att mäta deuteriumkinetiska isotopeffekter vid naturligt överflöd. Pascal och medarbetare testade sin hypotes genom att studera insättningsreaktionen av dimetyldiazomalonat i cyklohexan . Pascal et al. mätte en KIE på 2,2 med användning av ^2H
.
NMR för material med naturligt överflöd

Singleton och medarbetare visade kapaciteten hos ^13C
av
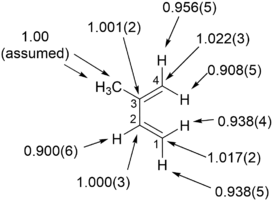
NMR-baserade naturliga mängd KIE-mätningar för att studera mekanismen för [4 + 2 ] cykloaddition isopren med maleinsyraanhydrid . Tidigare studier av Gajewski på isotopiskt berikade material observerade KIE-resultat som antydde ett asynkront övergångstillstånd, men var alltid konsekventa, inom fel, för en perfekt synkron reaktionsmekanism .

Detta arbete av Singleton et al. etablerade mätningen av flera ¹³
C
KIE:er inom designen av ett enda experiment. Dessa ^2H-
-
och ^{13C -}
KIE
mätningar bestämda vid naturlig överflöd fann att de "inre" vätena i dienen upplever en mer uttalad ²
H
KIE än de "utanför" vätena" och C1 och C4 upplever en signifikant KIE. Dessa nyckelobservationer tyder på en asynkron reaktionsmekanism för cykloaddition av isopren med maleinsyraanhydrid .

Begränsningarna för att bestämma KIE:s vid naturlig förekomst med NMR är att det återvunna materialet måste ha en lämplig mängd och renhet för NMR-analys (signalen av intresse bör vara skild från andra signaler), reaktionen av intresse måste vara irreversibel och reaktionsmekanismen får inte ändras under den kemiska reaktionens varaktighet .

Experimentella detaljer för användning av kvantitativ enkelpuls NMR för att mäta kinetisk isotopeffekt vid naturlig överflöd enligt följande: experimentet måste utföras under kvantitativa förhållanden inklusive en relaxationstid på 5 T 1, uppmätt 90° flipvinkel, en digital upplösning på _minst 5 punkter över en topp och ett signal:brus större än 250. Den råa FID:n är nollfylld till minst 256K punkter före Fouriertransformen. NMR-spektra fasas och behandlas sedan med en nollte ordningens baslinjekorrigering utan någon lutningskorrigering. Signalintegrationer bestäms numeriskt med en minimal tolerans för varje integrerad signal.

Exempel på belysande av organometalliska reaktionsmekanismer

Colletto et al. utvecklat en regioselektiv $\beta$ -arylering av benso[b]tiofener vid rumstemperatur med aryliodider som kopplingspartner och försökte förstå mekanismen för denna reaktion genom att utföra kinetiska isotopeffektmätningar av naturliga överflöd via enkelpuls NMR.

Regioselektiv $\beta$ -arylering av benso[b]tiofener

² H KIEs uppmätt vid naturlig förekomst

¹³ C KIEs mätt vid naturlig förekomst

Observationen av en primär ^13C -isotopeffekt vid C3, en omvänd ^2H -isotopeffekt, en sekundär ^13C -isotopeffekt vid C2 och avsaknaden av en ^2H -isotopeffekt vid C2 ledde till att Colletto et al. att föreslå en reaktionsmekanism av Heck-typ för den regioselektiva $\beta$ -aryleringen av benso[b]tiofener vid rumstemperatur med aryljodider som kopplingspartner.

Frost et al. försökte förstå effekterna av Lewis- syratillsatser på mekanismen för enantioselektiv palladiumkatalyserad CN-bindningsaktivering med hjälp av kinetiska isotopeffektmätningar med naturlig överflöd via enkelpuls NMR.

Enantioselektiv intramolekylär alkencyanoamidering

13C KIEs för enantioselektiv intramolekylär alkencyanoamideringsreaktion (vänster ingen tillsats, höger lägg till BPh ₃ )

Den primära ¹³ C kinetiska isotopeffekten som observerats i frånvaro av BPh ₃ antyder en reaktionsmekanism med hastighetsbegränsande cis-oxidation till C-CN-bindningen av cyanoformamiden. Tillsatsen av BPh ₃ orsakar en relativ minskning av den observerade ^13C kinetiska isotopeffekten vilket ledde till att Frost et al. att föreslå en förändring i det hastighetsbegränsande steget från cis-oxidation till koordinering av palladium till cyanoformamid.

DEPT-55 NMR

Även om mätningar av kinetiska isotopereffekter vid naturlig överflöd är ett kraftfullt verktyg för att förstå reaktionsmekanismer, kan mängderna material som krävs för analys göra denna teknik otillgänglig för reaktioner som använder dyra reagenser eller instabila utgångsmaterial. För att mildra dessa begränsningar utvecklade Jacobsen och medarbetare ¹ H till ¹³ C polarisationsöverföring som ett sätt att minska tiden och materialet som krävs för mätningar av kinetiska isotopeffekter vid naturligt överflöd. Den distorsionsfria förbättringen genom polarisationsöverföring (DEPT) drar fördel av det större gyromagnetiska förhållandet 1 ^H över ¹³ C för att teoretiskt förbättra mätningskänsligheten med en faktor 4 eller minska experimenttiden med en faktor 16. Denna metod för kinetisk isotopmätning av naturlig överflöd är fördelaktigt för analys för reaktioner som innehåller instabila utgångsmaterial och katalysatorer eller produkter som är relativt dyra.

Jacobsen och medarbetare identifierade den tiourea-katalyserade glykosyleringen av galaktos som en reaktion som uppfyllde båda de ovannämnda kriterierna (dyra material och instabila substrat) och var en reaktion med en dåligt förstådd mekanism. Glykosylering är ett specialfall av nukleofil substitution som saknar tydlig definition mellan SN ₁ och SN ₂ mekanistisk karaktär. Närvaron av syret intill platsen för förskjutning (dvs. C1) kan stabilisera positiv laddning. Denna laddningsstabilisering kan orsaka att alla potentiella samordnade vägar blir asynkrona och närmar sig intermediärer med oxokarbeniumkaraktär av S _N 1-mekanismen för glykosylering.

Reaktionsschema för tioureakatalyserad glykosylering av galaktos

¹³ C kinetiska isotopeffektmätningar för tioureakatalyserad glykosylering av galaktos

Jacobsen och medarbetare observerade små normala KIE vid C1, C2 och C5, vilket tyder på signifikant oxokarbeniumkaraktär i övergångstillståndet och en asynkron reaktionsmekanism med en stor grad av laddningsseparation.

Isotop-förhållande masspektrometri

High precision isotope-ratio mass spectrometri ( IRMS) är en annan metod för att mäta kinetisk fraktionering av isotoper för naturlig förekomst av KIE-mätningar. Widlanski och medarbetare visade ³⁴
S
KIE vid naturliga överflödsmätningar för hydrolys av sulfatmonoestrar . Deras observation av en stor KIE tyder på att SO-bindningsklyvning är hastighetskontrollerande och troligen utesluter en associerad reaktionsmekanism .

34S isotopeffekt på sulfatesterhydrolysreaktion

Den huvudsakliga begränsningen för att bestämma KIE vid naturlig överflöd med hjälp av IRMS är den nödvändiga platsselektiva nedbrytningen utan isotopfraktionering till en analyserbar liten molekyl, en icke-trivial uppgift.

Fallstudier

Primära väteisotopeffekter

Primära vätekinetiska isotopeffekter hänvisar till fall där en bindning till det isotopiskt märkta vätet bildas eller bryts i ett hastighets- och/eller produktbestämmande steg i en reaktion. Dessa är de vanligast uppmätta kinetiska isotopeffekterna, och mycket av den tidigare täckta teorin hänvisar till primära kinetiska isotopeffekter. När det finns tillräckliga bevis för att överföring av det märkta vätet sker i det hastighetsbestämmande steget av en reaktion, om en ganska stor kinetisk isotopeffekt observeras, t.ex. kH/kD på minst 5-6 eller kH/kT omkring 10–13 vid rumstemperatur är det ganska troligt att väteöverföringen är linjär och att vätet är ganska symmetriskt placerat i övergångstillståndet. Det är vanligtvis inte möjligt att kommentera tunnlingsbidrag till den observerade isotopeffekten om inte effekten är mycket stor. Om den primära kinetiska isotopeffekten inte är lika stor anses den i allmänhet vara indikativ för ett signifikant bidrag från tungatoms rörelse till reaktionskoordinaten, även om det också kan innebära att väteöverföringen följer en icke-linjär väg.

Sekundära väteisotopeffekter

De sekundära väteisotopeffekterna eller sekundär kinetisk isotopeffekt (SKIE) uppstår i fall där isotopsubstitutionen är långt ifrån att bindningen bryts. Den avlägsna atomen påverkar ändå de interna vibrationerna i systemet som via förändringar i nollpunktsenergin (ZPE) påverkar hastigheten för kemiska reaktioner. Sådana effekter uttrycks som förhållanden mellan hastigheten för den lätta isotopen och den för den tunga isotopen och kan vara "normala" (förhållandet är större än eller lika med 1) eller "inversa" (förhållandet är mindre än 1) effekter. SKIE definieras som α,β (etc.) sekundära isotopeffekter där sådana prefix hänvisar till positionen för isotopsubstitutionen i förhållande till reaktionscentrumet (se alfa- och beta-kol ). Prefixet α hänvisar till isotopen associerad med reaktionscentrumet medan prefixet β hänvisar till isotopen associerad med en atom som gränsar till reaktionscentrumet och så vidare.

Inom fysikalisk organisk kemi diskuteras SKIE i termer av elektroniska effekter som induktion, bindningshybridisering eller hyperkonjugering . Dessa egenskaper bestäms av elektronfördelning och beror på vibrationsmedelvärde för bindningslängd och vinklar som inte påverkas särskilt mycket av isotopsubstitution. Således avråds användningen av termen "elektronisk isotopeffekt" medan den är legitim, eftersom den kan misstolkas för att antyda att isotopeffekten är elektronisk till sin natur snarare än vibration.

SKIE:s kan förklaras i termer av förändringar i orbital hybridisering. När hybridiseringen av en kolatom ändras från sp ³ till sp ² påverkas ett antal vibrationslägen (sträckningar, böjning i planet och utanför planet). Böjningen i planet och utanför planet i ett sp3- ^hybridiserat kol är likartade i frekvens på grund av symmetrin hos ett sp3- ^hybridiserat kol. I ett sp ² hybridiserat kol är böjningen i planet mycket styvare än böjningen utanför planet, vilket resulterar i en stor skillnad i frekvensen, ZPE och därmed SKIE (som finns när det finns en skillnad i ZPE för reaktant och övergångstillstånd). Den teoretiska maximala förändringen som orsakas av böjfrekvensskillnaden har beräknats till 1,4.

När kol genomgår en reaktion som ändrar dess hybridisering från sp ³ till sp ² , är böjningskraftkonstanten utanför planet vid övergångstillståndet svagare eftersom det utvecklar sp ² -karaktär och en "normal" SKIE observeras med typiska värden på 1,1 till 1.2. Omvänt, när kolets hybridisering ändras från sp ² till sp ³ , ökar konstanterna för böjningskraft utanför planet vid övergångstillståndet och en omvänd SKIE observeras med typiska värden på 0,8 till 0,9.

Mer generellt kan SKIE för reversibla reaktioner vara "normal" åt det ena hållet och "omvänd" på det andra om bindningen i övergångstillståndet är halvvägs i styvhet mellan substrat och produkt, eller så kan de vara "normala" åt båda hållen om bindningen är svagare i övergångstillstånd, eller "omvänt" åt båda hållen om bindningen är starkare i övergångstillståndet än i någon av reaktanterna.

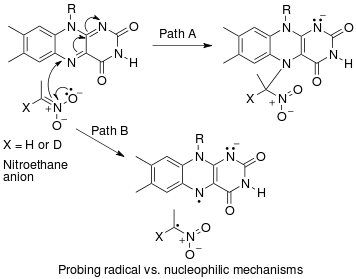
Ett exempel på en "omvänd" α sekundär kinetisk isotopeffekt kan ses i arbetet av Fitzpatrick och Kurtz som använde en sådan effekt för att skilja mellan två föreslagna vägar för reaktionen av d- aminosyraoxidas med nitroalkananjoner . Väg A involverade en nukleofil attack på koenzymet FAD , medan väg B involverar en friradikalmellanprodukt. Eftersom väg A resulterar i den mellanliggande kolförändrande hybridiseringen från sp ² till sp ³ förväntas en "omvänd" en SKIE. Om väg B inträffar bör ingen SKIE observeras eftersom den fria radikalintermediären inte ändrar hybridisering. En SKIE på 0,84 observerades och väg A verifierades som visas i schemat nedan.

Ett annat exempel på en SKIE är oxidationen av bensylalkoholer med dimetyldioxiran där tre övergångstillstånd för olika mekanismer föreslogs. Återigen, genom att överväga hur och om väteatomerna var inblandade i var och en, förutspådde forskare om de skulle förvänta sig en effekt av isotopsubstitution av dem eller inte. Sedan tillät analys av experimentella data för reaktionen dem att välja vilken väg som mest sannolikt var baserad på den observerade isotopeffekten.

Sekundära väteisotopeffekter från metylenväten användes också för att visa att Cope-omlagring i 1,5-hexadien följer en samordnad bindningsomlagringsväg, och inte en av de alternativt föreslagna allylradikal- eller 1,4-diyl-vägarna, som alla är presenteras i följande schema.

Alternativa mekanismer för Cope-omarrangemang av 1,5-hexadien: (uppifrån och ned), allylradikal, synkrona samordnade och 1,4-dyil-vägar. Den dominerande vägen visar sig vara den mellersta, som har sex delokaliserade π-elektroner som motsvarar en aromatisk mellanprodukt.

Steriska isotopeffekter

${\frac {k_{(X=D)}}{k_{(X=H)}}}=1.15$

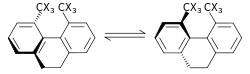
Den steriska isotopeffekten är en SKIE som inte involverar bindningsbrytning eller bildning. Denna effekt tillskrivs de olika vibrationsamplituderna hos isotopologer . Ett exempel på en sådan effekt är racemiseringen av 9,10-dihydro-4,5-dimetylfenantren. Den mindre vibrationsamplituden för deuterium jämfört med väte i C–H (kol–väte), C–D (kol–deuterium) bindningar resulterar i en mindre van der Waals radie eller effektiv storlek utöver en skillnad i ZPE mellan de två. När det finns en större effektiv bulk av molekyler som innehåller den ena över den andra kan detta manifesteras av en sterisk effekt på hastighetskonstanten. För exemplet ovan racemiserar deuterium snabbare än väteisotopologen vilket resulterar i en sterisk isotopeffekt. En modell för den steriska isotopeffekten utvecklades av Bartell. En sterisk isotopeffekt är vanligtvis liten, såvida inte transformationerna passerar genom ett övergångstillstånd med allvarlig sterisk belastning, som i racemiseringsprocessen som visas ovan.

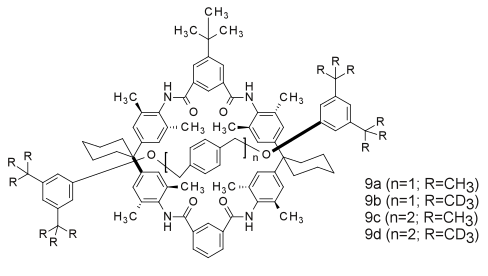
Ett annat exempel på den steriska isotopeffekten är rotaxaners glidningsreaktion. Deuteriumisotopen, på grund av sin mindre effektiva storlek, möjliggör enklare passage av propparna genom makrocykeln, vilket resulterar i snabbare avhalningshastigheter för de deutererade rotaxanerna .

Omvända kinetiska isotopeffekter

Reaktioner är kända där den deutererade arten reagerar snabbare än den undeutererade analogen, och dessa fall sägs uppvisa omvända kinetiska isotopeffekter (IKIE). _{Me2NCH2CH2NMe2} ) ₎ . IKIE : _{reduktiv eliminering} s observeras ofta vid av alkylmetallhydrider, t.ex. ( PtMe(H I sådana fall är CD-bindningen i övergångstillståndet, en agostisk art, mycket stabiliserad i förhållande till CH-bindningen.

En omvänd effekt kan också inträffa i en flerstegsreaktion om den totala hastighetskonstanten beror på en förjämvikt före det hastighetsbestämmande steget som har en omvänd jämviktsisotopeffekt . Till exempel är hastigheterna för syrakatalyserade reaktioner vanligtvis 2-3 gånger högre för reaktioner i D ₂ O katalyserad av D ₃ O ⁺ än för analoga reaktioner i H ₂ O katalyserad av H ₃ O ⁺ . Detta kan förklaras för en mekanism för specifik vätejonkatalys av en reaktant R genom _H3O ⁺ ( eller _D3O ⁺ ) .

H ₃ O ⁺ + R ⇌ RH ⁺ + H ₂ O

RH ⁺ + H ₂ O → H ₃ O ⁺ + P

Hastigheten för bildning av produkter är då d[P]/dt = k ₂ [RH ⁺ ] = k ₂ K ₁ [H ₃ O ⁺ ][R] = k _obs [H ₃ O ⁺ ][R]. I det första steget är H ₃ O ⁺ vanligtvis en starkare syra än RH ⁺ . Deuteration förskjuter jämvikten mot den starkare bundna syraarten RD ⁺ där effekten av deuteration på nollpunktsvibrationsenergin är större, så att den deutererade jämviktskonstanten K _1D är större än K _1H . Denna jämviktsisotopeffekt i det första steget uppväger vanligtvis den kinetiska isotopeffekten i det andra steget, så att det finns en uppenbar invers isotopeffekt och den observerade totala hastighetskonstanten k _obs = k ₂ K ₁ minskar.

Lösningsmedel väte kinetiska isotopeffekter

För att lösningsmedlets isotopeffekter ska vara mätbara måste en ändlig fraktion av lösningsmedlet ha en annan isotopsammansättning än resten. Därför måste stora mängder av de mindre vanliga isotoparterna finnas tillgängliga, vilket begränsar observerbara lösningsmedelsisotopeffekter till isotopsubstitutioner som involverar väte. Detekterbara kinetiska isotopeffekter inträffar endast när lösta ämnen byter väte med lösningsmedlet eller när det finns en specifik löst ämne-lösningsmedelsinteraktion nära reaktionsstället. Båda sådana fenomen är vanliga för protiska lösningsmedel, i vilka vätet är utbytbart, och de kan bilda dipol-dipol-interaktioner eller vätebindningar med polära molekyler.

Kol-13 isotopeffekter

De flesta organiska reaktioner involverar brytning och bildning av bindningar till ett kol; sålunda är det rimligt att förvänta sig påvisbara kolisotopeffekter. När ¹³ C används som märkning är förändringen i massan av isotopen endast ~8%, vilket begränsar de observerbara kinetiska isotopeffekterna till mycket mindre värden än de som kan observeras med väteisotopeffekter.

Kompenserar för variationer i ¹³ C naturligt överflöd

Ofta är den största felkällan i en studie som beror på den naturliga mängden kol den lilla variationen i naturligt ¹³ C-förekomst i sig. Sådana variationer uppstår eftersom utgångsmaterialen som används i reaktionen i sig är produkter av några andra reaktioner som har kinetiska isotopeffekter och motsvarande isotopberikningar i produkterna. För att kompensera för detta fel när NMR-spektroskopi används för att bestämma den kinetiska isotopeffekten, har följande riktlinjer föreslagits:

• Välj ett kol som är avlägset från reaktionscentrumet som kommer att fungera som referens och anta att det inte har en kinetisk isotopeffekt i reaktionen.
• I utgångsmaterialet som inte har genomgått någon reaktion, bestäm förhållandet mellan de andra kol-NMR-toppintegralerna och referenskolet.
• Erhåll samma förhållanden för kolen i ett prov av utgångsmaterialet efter att det har genomgått någon reaktion.
• ₀ Förhållandena mellan de senare förhållandena och de förra förhållandena ger R/R .

Om dessa liksom några andra försiktighetsåtgärder som listats av Jankowski följs, kan kinetiska isotopeffekter med en precision på tre decimaler uppnås.

Isotopeffekter med grundämnen tyngre än kol

Tolkning av kolisotopeffekter kompliceras vanligtvis genom att bindningar till kol samtidigt bildas och bryts. Även reaktioner som endast involverar bindningsklyvning från kolet, såsom SN ₁ -reaktioner, involverar förstärkning av de återstående bindningarna till kol. I många sådana reaktioner tenderar lämnande gruppisotopeffekter att vara lättare att tolka. Till exempel är substitutions- och elimineringsreaktioner där klor fungerar som en lämnande grupp bekväma att tolka, särskilt eftersom klor fungerar som en monoatomisk art utan inre bindning för att komplicera reaktionskoordinaten, och den har två stabila isotoper, 35 ^Cl och ³⁷ Cl , båda med hög överflöd. Den stora utmaningen för tolkningen av sådana isotopeffekter är lösningen av den lämnande gruppen.

På grund av experimentella osäkerheter kan mätning av isotopeffekt innebära betydande osäkerhet. Ofta bestäms isotopeffekter genom kompletterande studier på en serie isotopomerer. Följaktligen är det ganska användbart att kombinera väteisotopeffekter med tungatomisotopeffekter. Till exempel användes bestämning av kväveisotopeffekt tillsammans med väteisotopeffekt för att visa att reaktionen av 2-fenyletyltrimetylammoniumjon med etoxid i etanol vid 40 °C följer en E2-mekanism, i motsats till alternativa icke-koncentrerade mekanismer. Denna slutsats nåddes efter att ha visat att denna reaktion ger en kväveisotopeffekt, k ₁₄ / k ₁₅ , på 1,0133±0,0002 tillsammans med en kinetisk isotopeffekt av väte på 3,2 vid det utgående vätet.

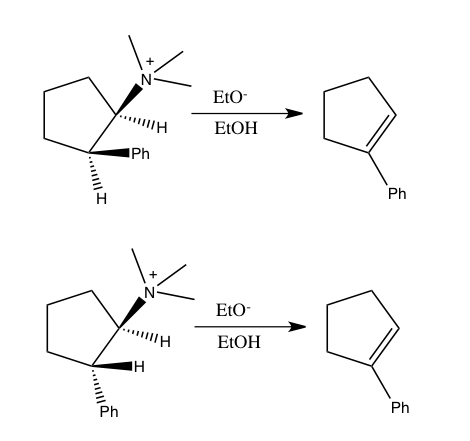
På liknande sätt användes en kombination av kväve- och väteisotopeffekter för att visa att syneliminering av enkla ammoniumsalter också följer en samordnad mekanism, vilket var en fråga om debatt tidigare. I följande två reaktioner av 2-fenylcyklopentyltrimetylammoniumjon med etoxid, som båda ger 1-fenylcyklopenten, uppvisade båda isomererna en kväveisotopeffekt k ₁₄ / k ₁₅ vid 60 °C. Även om reaktionen av trans-isomeren, som följer syn-eliminering, har en mindre kinetisk isotopeffekt av kväve (1,0064) jämfört med cis-isomeren som genomgår anti-eliminering (1,0108), är båda resultaten tillräckligt stora för att indikera försvagning av CN-bindningen i det övergångstillstånd som skulle inträffa i en samordnad process.

Andra exempel

Eftersom kinetiska isotopeffekter uppstår från skillnader i isotopmassor, är de största observerbara kinetiska isotopeffekterna förknippade med isotopsubstitutioner av väte med deuterium (100 % ökning i massa) eller tritium (200 % ökning i massa). Kinetiska isotopeffekter från isotopiska massförhållanden kan vara så stora som 36,4 med hjälp av myoner. De har producerat den lättaste väteatomen, ^0,11 H (0,113 amu), där en elektron kretsar runt en positiv myon (μ ⁺ ) "kärna" som har en massa på 206 elektroner. De har också framställt den tyngsta väteatomanalogen genom att ersätta en elektron i helium med en negativ myon (μ − ) ^för att bilda Heμ med en atommassa på 4,116 amu. Eftersom den negativa myonen är mycket tyngre än en elektron, kretsar den mycket närmare kärnan, vilket effektivt skyddar en proton, vilket får Heμ att bete sig som ^{4,1 H. Med dessa exotiska arter} undersöktes reaktionen mellan H och ¹ H _{2 .} Hastighetskonstanter från att reagera de lättaste och tyngsta väteanalogerna med ¹ H ₂ användes sedan för att beräkna den kinetiska isotopeffekten k _0,11 / k _{4,1 , där det finns en 36,4-faldig skillnad i isotopmassor.} För denna reaktion råkar isotopsubstitution ge en omvänd kinetisk isotopeffekt, och författarna rapporterar en kinetisk isotopeffekt så låg som 1,74 x 10-4, ^vilket är den minsta kinetiska isotopeffekt som någonsin rapporterats.

Den kinetiska isotopeffekten leder till en specifik fördelning av deuteriumisotoper i naturprodukter, beroende på vägen de syntetiserades i naturen. Med NMR-spektroskopi är det därför lätt att upptäcka om alkoholen i vin har jäst från glukos eller från otillåtet tillsatt sackaros .

En annan reaktionsmekanism som belystes med hjälp av den kinetiska isotopeffekten är halogeneringen av toluen :

I denna speciella "intramolekylära KIE"-studie genomgår ett bensyliskt väte radikalsubstitution med brom med användning av N -bromsuccinimid som bromeringsmedlet. Det visade sig att PhCH ₃ bromerar 4,86 ​​gånger snabbare än PhCD ₃ . En stor KIE på 5,56 är associerad med reaktionen mellan ketoner och brom och natriumhydroxid .

I denna reaktion är det hastighetsbegränsande steget bildning av enolatet genom deprotonering av ketonen. I denna studie beräknas KIE från reaktionshastighetskonstanterna för vanlig 2,4-dimetyl-3-pentanon och dess deutererade isomer genom optiska densitetsmätningar .

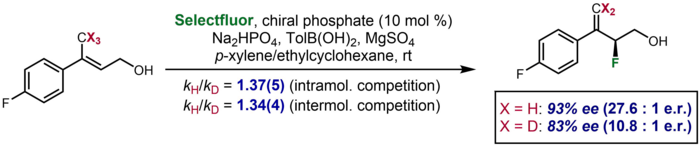
I asymmetrisk katalys finns det sällsynta fall där en kinetisk isotopeffekt visar sig som en signifikant skillnad i enantioselektiviteten som observeras för ett deutererat substrat jämfört med ett icke-deutererat. Ett exempel rapporterades av Toste och medarbetare, där ett deutererat substrat gav en enantioselektivitet på 83 % ee, jämfört med 93 % ee för det odeutererade substratet. Effekten togs för att bekräfta ytterligare inter- och intramolekylär konkurrens KIE-data som antydde klyvning av CH/D-bindningen i enantiodbestämningssteget.

Se även

• Crossover-experiment (kemi)
• Jämviktskonstant#Effekt av isotopsubstitution
• Isotopeffekt på lipidperoxidation
• Kinetiska isotopeffekter av RuBisCO (ribulos-1,5-bisfosfatkarboxylasoxygenas)
• Magnetisk isotopeffekt
• Reaktionsmekanism
• Övergående kinetisk isotopfraktionering
• Urey-Bigeleisen-Mayer ekvation

Vidare läsning

•   Bell RP, Crooks JE (20 juli 1965). "Kinetiska väteisotopeffekter vid jonisering av vissa ketoniska ämnen". Proceedings of the Royal Society of London A . 286 (1406): 285–299. Bibcode : 1965RSPSA.286..285B . doi : 10.1098/rspa.1965.0144 . S2CID 96761478 .