Övergångstillståndsteori

1 : Reaktionskoordinatdiagram för den bimolekylära nukleofila substitutionsreaktionen (SN 2 ₎ mellan brommetan och hydroxidanjonen

Inom kemi förklarar övergångstillståndsteori ( TST ) reaktionshastigheterna för elementära kemiska reaktioner . Teorin antar en speciell typ av kemisk jämvikt (kvasijämvikt) mellan reaktanter och aktiverade övergångstillståndskomplex .

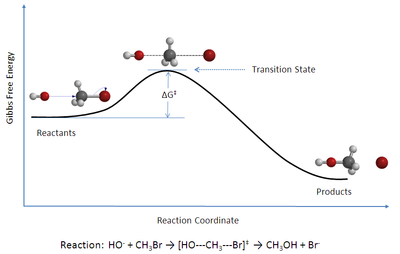
TST används främst för att kvalitativt förstå hur kemiska reaktioner sker. TST har varit mindre framgångsrikt i sitt ursprungliga mål att beräkna absoluta reaktionshastighetskonstanter eftersom beräkningen av absoluta reaktionshastigheter kräver exakt kunskap om potentiella energiytor, men det har varit framgångsrikt med att beräkna standardentalpin för aktivering (Δ H ^‡ , även skrivet Δ ^‡ H ^ɵ ), standardentropin för aktivering (Δ S ^‡ eller Δ ^‡ S ^ɵ ), och standard Gibbs aktiveringsenergi (Δ G ^‡ eller Δ ^‡ G ^ɵ ) för en viss reaktion om dess hastighetskonstant har bestämts experimentellt . ( ^‡ hänvisar till värdet av intresse vid övergångstillståndet ; Δ H ^‡ är skillnaden mellan entalpin för övergångstillståndet och reaktanternas.)

Denna teori utvecklades samtidigt 1935 av Henry Eyring , sedan vid Princeton University , och av Meredith Gwynne Evans och Michael Polanyi från University of Manchester . TST hänvisas också till som "aktiverad-komplex teori", "absolut-hastighetsteori" och "teori om absoluta reaktionshastigheter".

Före utvecklingen av TST användes Arrhenius hastighetslag allmänt för att bestämma energier för reaktionsbarriären. Arrhenius- ekvationen härrör från empiriska observationer och ignorerar alla mekanistiska överväganden, såsom om en eller flera reaktiva intermediärer är involverade i omvandlingen av en reaktant till en produkt. Därför var ytterligare utveckling nödvändig för att förstå de två parametrarna _associerade med denna lag, den preexponentiella faktorn ( A ) och aktiveringsenergin ( Ea ). TST, som ledde till Eyring-ekvationen , behandlar framgångsrikt dessa två frågor; dock gick det 46 år mellan publiceringen av Arrhenius-kurslagen 1889 och Eyring-ekvationen som härleddes från TST 1935. Under den perioden bidrog många vetenskapsmän och forskare avsevärt till utvecklingen av teorin.

Teori

De grundläggande idéerna bakom övergångstillståndsteorin är följande:

1. Reaktionshastigheter kan studeras genom att undersöka aktiverade komplex nära sadelpunkten på en potentiell energiyta . Detaljerna om hur dessa komplex bildas är inte viktiga. Själva sadelpunkten kallas för övergångstillstånd.
2. De aktiverade komplexen befinner sig i en speciell jämvikt (kvasijämvikt) med reaktantmolekylerna.
3. De aktiverade komplexen kan omvandlas till produkter, och kinetisk teori kan användas för att beräkna hastigheten för denna omvandling.

Utveckling

Vid utvecklingen av TST togs tre tillvägagångssätt som sammanfattas nedan

Termodynamisk behandling

År 1884 föreslog Jacobus van 't Hoff Van 't Hoff-ekvationen som beskrev temperaturberoendet för jämviktskonstanten för en reversibel reaktion:

${\ce {{A}<=> {B}}}$

${\frac {d\ln K}{ dT}}={\frac {\Delta U}{RT^{2}}}$

där Δ U är förändringen i intern energi, K är jämviktskonstanten för reaktionen, R är den universella gaskonstanten och T är termodynamisk temperatur . Baserat på experimentellt arbete föreslog Svante Arrhenius 1889 ett liknande uttryck för hastighetskonstanten för en reaktion, givet enligt följande:

${\frac {d\ln k}{dT}}={\frac {\Delta E}{RT^{2}}}$

Integration av detta uttryck leder till Arrhenius-ekvationen

$k=Ae^{-E_{a}/RT}$

där k är hastighetskonstanten. A kallades frekvensfaktorn (nu kallad pre-exponentiell koefficient), och E _a betraktas som aktiveringsenergin. I början av 1900-talet hade många accepterat Arrhenius-ekvationen, men den fysiska tolkningen av A och E _a förblev vag. Detta fick många forskare inom kemisk kinetik att erbjuda olika teorier om hur kemiska reaktioner inträffade i ett försök att relatera A och E _a till den molekylära dynamik som är direkt ansvarig för kemiska reaktioner.

1910 introducerade den franske kemisten René Marcelin begreppet Gibbs standardaktiveringsenergi. Hans relation kan skrivas som

$k\propto \exp \left({\frac {-\Delta ^{\ddagger }G^{\ominus }}{RT}}\right)$

Ungefär samtidigt som Marcelin arbetade med sin formulering introducerade de holländska kemisterna Philip Abraham Kohnstamm, Frans Eppo Cornelis Scheffer och Wiedold Frans Brandsma standardaktiveringsentropi och standardaktiveringsentalpi. De föreslog följande ekvation för hastighetskonstant

$k\propto \exp \left({\frac {\Delta ^{\dagger }S^{\ominus } }{R}}\right)\exp \left({\frac {-\Delta ^{\ddagger }H^{\ominus }}{RT}}\right)$

Konstantens natur var dock fortfarande oklar.

Kinetisk-teoretisk behandling

I början av 1900 studerade Max Trautz och William Lewis reaktionshastigheten med hjälp av kollisionsteori , baserad på den kinetiska teorin om gaser . Kollisionsteorin behandlar reagerande molekyler som hårda sfärer som kolliderar med varandra; denna teori försummar entropiförändringar, eftersom den antar att kollisionen mellan molekyler är helt elastisk.

Lewis tillämpade sin behandling på följande reaktion och fick god överensstämmelse med experimentellt resultat.

2HI → _H2 + _I2

Men senare när samma behandling tillämpades på andra reaktioner fanns det stora skillnader mellan teoretiska och experimentella resultat.

Statistisk-mekanisk behandling

Statistisk mekanik spelade en betydande roll i utvecklingen av TST. Tillämpningen av statistisk mekanik på TST utvecklades dock mycket långsamt med tanke på det faktum att James Clerk Maxwell , Ludwig Boltzmann och Leopold Pfaundler i mitten av 1800-talet publicerade flera artiklar som diskuterade reaktionsjämvikt och -hastigheter i termer av molekylära rörelser och den statistiska fördelningen av molekylära hastigheter.

Det var inte förrän 1912 när den franske kemisten A. Berthoud använde Maxwell–Boltzmanns distributionslag för att få ett uttryck för hastighetskonstanten.

${\frac {d\ln k}{dT}}={\frac {a-bT}{RT^{2}}}$

där a och b är konstanter relaterade till energitermer.

Två år senare gjorde René Marcelin ett viktigt bidrag genom att behandla en kemisk reaktions förlopp som en rörelse av en punkt i fasrummet . Han tillämpade sedan Gibbs statistisk-mekaniska förfaranden och fick ett uttryck som liknar det han hade erhållit tidigare från termodynamisk övervägande.

1915 kom ett annat viktigt bidrag från den brittiske fysikern James Rice. Baserat på sin statistiska analys drog han slutsatsen att hastighetskonstanten är proportionell mot den "kritiska ökningen". Hans idéer utvecklades vidare av Richard Chace Tolman . År 1919 tillämpade den österrikiska fysikern Karl Ferdinand Herzfeld statistisk mekanik på jämviktskonstanten och kinetisk teori på hastighetskonstanten för den omvända reaktionen, k ₋₁ , för reversibel dissociation av en diatomisk molekyl.

${\ce {AB <=>[k_1][k_{-1}] {A}+ {B}}}$

Han erhöll följande ekvation för hastighetskonstanten för framåtreaktionen

$k_{1}={\frac {k_{\mathrm {B} }T}{ h}}\left(1-e^{-{\frac {h\nu}{k_{\text{B}}T}}}\right)\exp \left({\frac {-E^{\ ominus }}{RT}}\right)$

där $\textstyle E^{\ominus }$ är dissociationsenergin vid absoluta noll, k _B är Boltzmann-konstanten , h är Planck-konstanten , T är termodynamisk temperatur, $\nu$ är vibrations bindningens frekvens . Detta uttryck är mycket viktigt eftersom det är första gången som faktorn k _B T / h , som är en kritisk komponent i TST, har förekommit i en hastighetsekvation.

1920 vidareutvecklade den amerikanske kemisten Richard Chace Tolman Rices idé om det kritiska inkrementet. Han drog slutsatsen att kritisk ökning (nu kallad aktiveringsenergi) av en reaktion är lika med medelenergin för alla molekyler som genomgår reaktion minus medelenergin för alla reaktantmolekyler.

Potentiella energiytor

Konceptet med potentiell energiyta var mycket viktigt i utvecklingen av TST. Grunden till detta koncept lades av René Marcelin 1913. Han teoretiserade att en kemisk reaktions framsteg kunde beskrivas som en punkt i en potentiell energiyta med koordinater i atomärt moment och avstånd.

1931 konstruerade Henry Eyring och Michael Polanyi en potentiell energiyta för reaktionen nedan. Denna yta är ett tredimensionellt diagram baserat på kvantmekaniska principer samt experimentella data om vibrationsfrekvenser och dissociationsenergier.

H + H2 _→ H2 ₊ H

Ett år efter Eyring och Polanyi-konstruktionen gjorde Hans Pelzer och Eugene Wigner ett viktigt bidrag genom att följa utvecklingen av en reaktion på en potentiell energiyta. Vikten av detta arbete var att det var första gången som begreppet kol eller sadelpunkt i den potentiella energiytan diskuterades. De drog slutsatsen att reaktionshastigheten bestäms av systemets rörelse genom den kol.

Det har typiskt antagits att den hastighetsbegränsande eller lägsta sadelpunkten är belägen på samma energiyta som det initiala marktillståndet. Det har dock nyligen upptäckts att detta kan vara felaktigt för processer som sker i halvledare och isolatorer, där ett initialt exciterat tillstånd kan gå genom en sadelpunkt lägre än den på ytan av det initiala grundtillståndet.

Kramers teori om reaktionshastigheter

Genom att modellera reaktioner som Langevins rörelse längs en endimensionell reaktionskoordinat, kunde Hendrik Kramers härleda ett samband mellan formen på den potentiella energiytan längs reaktionskoordinaten och systemets övergångshastigheter. Formuleringen bygger på att approximera det potentiella energilandskapet som en serie harmoniska brunnar. I ett tvåstatssystem kommer det att finnas tre brunnar; en brunn för tillstånd A, en upp och nedvänd brunn som representerar den potentiella energibarriären och en brunn för tillstånd B. Övergångshastigheten från tillstånd A till B är relaterad till brunnarnas resonansfrekvens via

$k^{A\rightarrow B}={\frac {\omega _{a}\omega _ {H}}{2\pi \gamma }}\exp \left(-{\frac {E_{H}-E_{A}}{k_{\text{B}}T}}\right)$

där $\omega _{a}$ är brunnens frekvens för tillstånd A, $\omega _{H}$ är barriärbrunnens frekvens, $\gamma$ är den viskösa dämpningen, $E_{H}$ är energin från toppen av barriären, $E_{a}$ är energin från botten av brunnen för tillstånd A, och $k_{\text{B}}T$ är systemets temperatur gånger Boltzmann-konstanten.

Motivering för Eyrings ekvation

En av de viktigaste egenskaperna som introducerades av Eyring , Polanyi och Evans var uppfattningen att aktiverade komplex är i kvasi-jämvikt med reaktanterna. Hastigheten är då direkt proportionell mot koncentrationen av dessa komplex multiplicerat med frekvensen ( k _B T / h ) med vilken de omvandlas till produkter. Nedan ges ett icke rigoröst rimlighetsargument för den funktionella formen av Eyring-ekvationen. Den viktigaste statistiska mekaniska faktorn k _B T / h kommer dock inte att vara motiverad, och argumentet som presenteras nedan utgör inte en sann "härledning" av Eyrings ekvation.

Kvasi-jämviktsantagande

Kvasijämvikt skiljer sig från klassisk kemisk jämvikt, men kan beskrivas med en liknande termodynamisk behandling. Betrakta reaktionen nedan

${\ce {{A}+{B}<=>{[AB]^{\dagger }}->{P}}}$

Figur 2: Potentiell energidiagram

där fullständig jämvikt uppnås mellan alla arter i systemet inklusive aktiverade komplex, [AB] ^‡ . Med hjälp av statistisk mekanik kan koncentrationen av [AB] ^‡ beräknas i termer av koncentrationen av A och B.

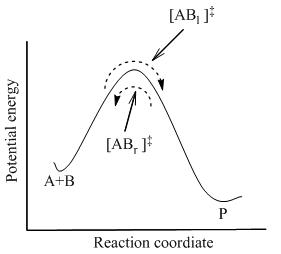
TST antar att även när reaktanterna och produkterna inte är i jämvikt med varandra, är de aktiverade komplexen i kvasi-jämvikt med reaktanterna. Som illustreras i figur 2 finns det när som helst ett fåtal aktiverade komplex, och några var reaktantmolekyler i det omedelbara förflutna, som betecknas [ABl] ‡ ( _eftersom de ^rör sig från vänster till höger). Resten av dem var produktmolekyler i det omedelbara förflutna ([AB r _] ^‡ ).

I TST antas det att flödet av aktiverade komplex i de två riktningarna är oberoende av varandra. Det vill säga, om alla produktmolekyler plötsligt avlägsnades från reaktionssystemet, stannar flödet av [AB _r ] ^‡ , men det finns fortfarande ett flöde från vänster till höger. Därför, för att vara tekniskt korrekt, är reaktanterna i jämvikt endast med [AB _l ] ^‡ , de aktiverade komplexen som var reaktanter i det omedelbara förflutna.

Plausibilitetsargument

De aktiverade komplexen följer inte en Boltzmann-fördelning av energier, men en "jämviktskonstant" kan ändå härledas från den fördelning de följer. Jämviktskonstanten K ‡ ^för kvasi-jämvikten kan skrivas som

$K^{\ddagger }={\frac {\ce {[AB]^{\ddagger }}}{\ce {[A][B] }}}$ .

är den kemiska aktiviteten för övergångstillståndet AB ^‡

$[{\ce {AB}}]^{\ddagger }=K^{\ddagger [{\ce {A}}][{\ce {B}}]$ .

Därför är hastighetsekvationen för produktionen av produkten

${\frac {d[{\ce {P}}]} {dt}}=k^{\ddagger [{\ce {AB}}]^{\ddagger }=k^{\ddagger }K^{\ddagger [{\ce {A}}][{\ ce {B}}]=k[{\ce {A}}][{\ce {B}}]$ ,

där hastighetskonstanten k ges av

$k=k^{\ddagger }K^{\ddagger }$ .

Här är k ^‡ direkt proportionell mot frekvensen av vibrationsläget som ansvarar för omvandlingen av det aktiverade komplexet till produkten; frekvensen för detta vibrationsläge är $\nu$ . Varje vibration leder inte nödvändigtvis till att produkten bildas, så en proportionalitetskonstant ${\displaystyle \kappa } ,$ kallad transmissionskoefficienten, introduceras för att ta hänsyn till denna effekt. Så k ^‡ kan skrivas om som

$k^{\ddagger }=\kappa \nu$ .

För jämviktskonstanten K ^‡ leder statistisk mekanik till ett temperaturberoende uttryck givet som

$K^{\ddagger }={\frac {k_{\text{B}}T}{h\nu }}K^{\ddagger '}$ ( ${\displaystyle K^{\ddagger '}=:e^{\frac {-\Delta G^{\ddagger }}{RT}}} )$ .

Genom att kombinera de nya uttrycken för k ^‡ och K ^‡ kan ett nytt hastighetskonstant uttryck skrivas, vilket ges som

$\displaystyle k=k^{\ddagger }K^{\ddagger }=\kappa {\ frac {k_{\text{B}}T}{h}}e^{\frac {-\Delta G^{\ddagger }}{RT}}=\kappa {\frac {k_{\text{B} }T}{h}}K^{\ddagger '}}$ .

Eftersom, per definition, Δ G ^‡ = Δ H ^‡ – T Δ S ^‡ , kan hastighetskonstantens uttryck utökas för att ge en alternativ form av Eyrings ekvation:

$k=\kappa {\frac {k_{\text{B}}T}{h}}e^{\frac { \Delta S^{\ddagger }}{R}}e^{\frac {-\Delta H^{\ddagger }}{RT}}$ .

För korrekt dimensionalitet måste ekvationen ha en extra faktor på ( c ^⊖ ) ^{1– m} för reaktioner som inte är unimolekylära:

$k=\kappa {\frac {k_{\text{B}}T}{h} }e^{\frac {\Delta S^{\ddagger }}{R}}e^{\frac {-\Delta H^{\ddagger }}{RT}}(c^{\ominus })^{ 1-m}$ ,

där c ^⊖ är standardkoncentrationen 1 mol⋅L ^–1 och m är molekylariteten.

Slutsatser från övergångstillståndsteori och förhållande till Arrheniusteori

Hastighetskonstantens uttryck från teorin om övergångstillstånd kan användas för att beräkna Δ G ^‡ , Δ H ^‡ , Δ S ^‡ , och även Δ V ^‡ (aktiveringsvolymen) med användning av experimentell hastighetsdata. Dessa så kallade aktiveringsparametrar ger insikt i karaktären av ett övergångstillstånd , inklusive energiinnehåll och ordningsgrad, jämfört med utgångsmaterialen och har blivit ett standardverktyg för att belysa reaktionsmekanismer inom fysikalisk organisk kemi . Den fria energin för aktivering, Δ G ^‡ , definieras i övergångstillståndsteorin att vara energin sådan att ${\displaystyle \Delta G^{\dagger }=-RT\$ = håller. Parametrarna Δ H ^‡ och Δ S ^‡ kan sedan härledas genom att bestämma Δ G ^‡ = Δ H ^‡ – T Δ S ^‡ vid olika temperaturer.

Eftersom den funktionella formen av Eyring- och Arrheniusekvationerna liknar varandra, är det frestande att relatera aktiveringsparametrarna till aktiveringsenergin och pre-exponentiella faktorer för Arrhenius-behandlingen. Arrhenius-ekvationen härleddes dock från experimentella data och modellerar den makroskopiska hastigheten med endast två parametrar, oavsett antalet övergångstillstånd i en mekanism. Däremot kan aktiveringsparametrar hittas för varje övergångstillstånd för en flerstegsmekanism, åtminstone i princip. Således, även om aktiveringsentalpin, Δ H ^‡ , ofta likställs med Arrhenius aktiveringsenergi E _a , är de inte ekvivalenta. För ett reaktionssteg i kondenserad fas (t.ex. lösningsfas) eller en molekylär gasfasreaktion, E _a = Δ H ^‡ + RT . För andra gasfasreaktioner är E _a = Δ H ^‡ + (1 − Δ n ^‡ ) RT , där Δ n ^‡ är förändringen i antalet molekyler vid bildandet av övergångstillståndet. (För en bimolekylär gasfasprocess är alltså E _a = Δ H ^‡ + 2 RT. )

Aktiveringsentropin, AS ‡ ^, ger i vilken utsträckning övergångstillståndet (inklusive eventuella lösningsmedelsmolekyler involverade i eller störda av reaktionen) är mer oordnat jämfört med utgångsmaterialen. Det ger en konkret tolkning av den pre-exponentiella faktorn A i Arrhenius-ekvationen; för en unimolekylär, enstegsprocess, den grova ekvivalensen A = ( k _B T / h ) exp(1 + Δ S ^‡ / R ) (eller A = ( k _B T / h ) exp(2 + Δ S ^‡ / R ) för bimolekylära gasfasreaktioner) gäller. För en unimolekylär process indikerar ett negativt värde ett mer ordnat, styvt övergångstillstånd än grundtillståndet, medan ett positivt värde återspeglar ett övergångstillstånd med lösare bindningar och/eller större konformationell frihet. Det är viktigt att notera att, av dimensionsskäl, reaktioner som är bimolekylära eller högre har Δ S ^‡ -värden som beror på det valda standardtillståndet (standardkoncentration, i synnerhet). För de senaste publikationerna väljs 1 mol L ^{–1 eller 1 molar.} Eftersom detta val är en mänsklig konstruktion, baserat på våra definitioner av enheter för molär kvantitet och volym, är storleken och tecknet på Δ S ^‡ för en enstaka reaktion meningslösa i sig; endast jämförelser av värdet med värdet för en referensreaktion av "känd" (eller antagen) mekanism, gjord i samma standardtillstånd, är giltig.

Aktiveringsvolymen hittas genom att ta partialderivatan av Δ G ^‡ med avseende på trycket (håller temperaturen konstant): $\Delta V^{\dolk }:=(\partial \Delta G^{\ddagger }/\partial P)_{T}$ . Den ger information om storleken och därmed graden av bindning vid övergångstillståndet. En associativ mekanism kommer sannolikt att ha en negativ volym av aktivering, medan en dissociativ mekanism sannolikt kommer att ha ett positivt värde.

Givet förhållandet mellan jämviktskonstanten och framåt- och bakåthastighetskonstanterna, $K=k_{1}/k_{-1}$ , antyder Eyring-ekvationen att

$\Delta G^{\circ }=\Delta G_{1}^{\ddagger }-\Delta G_{-1}^{\ddagger }$ .

En annan implikation av TST är Curtin-Hammett-principen : produktförhållandet för en kinetiskt kontrollerad reaktion från R till två produkter A och B kommer att återspegla skillnaden i energierna för de respektive övergångstillstånden som leder till produkten, förutsatt att det finns en enda övergång ange till var och en:

${\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}=e^{-\Delta \Delta G^{\ddagger }/RT}$ ( ${\displaystyle \Delta \Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^ {\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }} )$ .

(I uttrycket för ΔΔ G ^‡ ovan finns det en extra $\Delta G^{\circ }=G_{\mathrm {S} _{\mathrm {A} }}^{\circ }-G_{\mathrm {S} _{\mathrm {B} }}^{\circ }$ term om A och B bildas av två olika arter S _A och S _B i jämvikt.)

För en termodynamiskt kontrollerad reaktion resulterar varje skillnad på RT ln 10 ≈ (1,987 × 10 ^–3 kcal/mol K)(298 K)(2,303) ≈ 1,36 kcal/mol i de fria energierna för produkterna A och B i en faktor av 10 i selektivitet vid rumstemperatur (298 K), en princip som kallas "1,36-regeln":

${\frac {[\mathrm {A} ]}{[\mathrm {B} ]}}= 10^{-\Delta G^{\circ }/(1,36\ \mathrm {kcal/mol} )}$ ( ${\displaystyle \Delta G^{\circ }= G_{\mathrm {A} }^{\circ }-G_{\mathrm {B} }^{\circ }})$ .

Analogt resulterar varje skillnad på 1,36 kcal/mol i aktiveringsenergin i en faktor 10 i selektivitet för en kinetiskt kontrollerad process vid rumstemperatur:

${\displaystyle {\frac {[\mathrm {A} ]}{[\mathrm {B} ]}} =10^{-\Delta \Delta G^{\ddagger }/(1,36\ \mathrm {kcal/mol} )}} ( Δ Δ G ‡$ = $\ Delta G^{\ddagger }=\Delta G_{\mathrm {A} }^{\ddagger }-\Delta G_{\mathrm {B} }^{\ddagger }})$ .

Med Eyring-ekvationen finns det ett enkelt samband mellan Δ G ^‡ , första ordningens hastighetskonstanter och reaktionshalveringstid vid en given temperatur. Vid 298 K har en reaktion med Δ G ^‡ = 23 kcal/mol en hastighetskonstant på k ≈ 8,4 × 10 ^–5 s ^–1 och en halveringstid på t _1/2 ≈ 2,3 timmar, siffror som ofta avrundas till k ~ 10 ^–4 s ^–1 och t _1/2 ~ 2 timmar. Således motsvarar en fri aktiveringsenergi av denna storlek en typisk reaktion som fortsätter till fullbordan över natten vid rumstemperatur. Som jämförelse har cyklohexanstolen en Δ G ^‡ på cirka 11 kcal/mol med k ~ 10 ⁵ s ^–1 , vilket gör det till en dynamisk process som sker snabbt (snabbare än NMR-tidsskalan) vid rumstemperatur. I andra änden av skalan har cis/trans- isomeriseringen av 2-buten en Δ G ^‡ på cirka 60 kcal/mol, motsvarande k ~ 10 ^–31 s ^–1 vid 298 K. Detta är en försumbar hastighet: halveringstiden är 12 storleksordningar längre än universums ålder .

Begränsningar

Generellt sett har TST gett forskare en konceptuell grund för att förstå hur kemiska reaktioner sker. Även om teorin är allmänt användbar har den begränsningar. Till exempel, när den tillämpas på varje elementärt steg i en flerstegsreaktion, antar teorin att varje mellanprodukt är tillräckligt långlivad för att nå en Boltzmann-fördelning av energier innan den fortsätter till nästa steg. När mellanprodukterna är mycket kortlivade misslyckas TST. I sådana fall kan rörelsemängden för reaktionsbanan från reaktanterna till mellanprodukten fortsätta för att påverka produktselektiviteten (ett exempel på en sådan reaktion är den termiska nedbrytningen av diazaobicyklopentaner, presenterad av Anslyn och Dougherty ) .

Övergångstillståndsteorin bygger också på antagandet att atomkärnor beter sig enligt klassisk mekanik . Det antas att om inte atomer eller molekyler kolliderar med tillräckligt med energi för att bilda övergångsstrukturen så sker inte reaktionen. Men enligt kvantmekaniken, för varje barriär med en ändlig mängd energi, finns det en möjlighet att partiklar fortfarande kan tunnla över barriären. När det gäller kemiska reaktioner betyder det att det finns en chans att molekyler reagerar, även om de inte kolliderar med tillräckligt med energi för att övervinna energibarriären. Även om denna effekt är försumbar för reaktioner med stora aktiveringsenergier, blir den ett viktigt fenomen för reaktioner med relativt låga energibarriärer, eftersom sannolikheten för tunnling ökar med minskande barriärhöjd.

Teorin om övergångstillstånd misslyckas för vissa reaktioner vid hög temperatur. Teorin antar att reaktionssystemet kommer att passera över den lägsta energisadelpunkten på den potentiella energiytan. Även om denna beskrivning är konsekvent för reaktioner som inträffar vid relativt låga temperaturer, vid höga temperaturer, befolkar molekyler vibrationsmoder med högre energi; deras rörelse blir mer komplex och kollisioner kan leda till övergångstillstånd långt bort från den lägsta energisadelpunkten. Denna avvikelse från teorin om övergångstillstånd observeras även i den enkla utbytesreaktionen mellan diatomiskt väte och en väteradikal.

Med tanke på dessa begränsningar har flera alternativ till teorin om övergångstillstånd föreslagits. En kort diskussion om dessa teorier följer.

Generaliserad övergångstillståndsteori

Varje form av TST, såsom mikrokanonisk variations-TST, kanonisk variations-TST och förbättrad kanonisk variations-TST, där övergångstillståndet inte nödvändigtvis är beläget vid sadelpunkten, hänvisas till som generaliserad övergångstillståndsteori.

Mikrokanonisk variations-TST

En grundläggande brist i övergångstillståndsteorin är att den räknar varje korsning av övergångstillståndet som en reaktion från reaktanter till produkter eller vice versa. I verkligheten kan en molekyl korsa denna "delande yta" och vända sig om, eller korsa flera gånger och bara reagera en gång. Som sådan sägs ojusterad TST tillhandahålla en övre gräns för hastighetskoefficienterna. För att korrigera för detta varierar teorin om variationsövergångstillstånd platsen för den delningsyta som definierar en framgångsrik reaktion för att minimera hastigheten för varje fast energi. Hastighetsuttrycken som erhålls i denna mikrokanoniska behandling kan integreras över energin, med hänsyn tagen till den statistiska fördelningen över energitillstånd, för att ge de kanoniska eller termiska hastigheterna.

Kanonisk variations-TST

En utveckling av övergångstillståndsteori där positionen för delningsytan varieras för att minimera hastighetskonstanten vid en given temperatur.

Förbättrad kanonisk variations-TST

En modifiering av teorin om kanonisk variationsövergångstillstånd där, för energier under tröskelenergin, läget för den delande ytan anses vara den för den mikrokanoniska tröskelenergin. Detta tvingar bidragen till hastighetskonstanter att vara noll om de ligger under tröskelenergin. En kompromissdelningsyta väljs sedan för att minimera bidragen till hastighetskonstanten som görs av reaktanter med högre energier.

Nonadiabatisk TST

En expansion av TST till reaktionerna när två spin-tillstånd är inblandade samtidigt kallas nonadiabatic transition state theory (NA-TST) .

Semiklassisk TST

Med hjälp av vibrationsstörningsteori kan effekter som tunnling och variationseffekter redovisas inom SCTST- formalismen.

Ansökningar

Enzymatiska reaktioner

Enzymer katalyserar kemiska reaktioner med hastigheter som är häpnadsväckande i förhållande till okatalyserad kemi vid samma reaktionsförhållanden. Varje katalytisk händelse kräver minst tre eller ofta fler steg, som alla sker inom de få millisekunder som kännetecknar typiska enzymatiska reaktioner. Enligt övergångstillståndsteorin spenderas den minsta delen av den katalytiska cykeln i det viktigaste steget, det i övergångstillståndet. De ursprungliga förslagen till teorin om absolut reaktionshastighet för kemiska reaktioner definierade övergångstillståndet som en distinkt art i reaktionskoordinaten som bestämde den absoluta reaktionshastigheten. Strax därefter Linus Pauling att den kraftfulla katalytiska verkan av enzymer kunde förklaras av specifik tät bindning till övergångstillståndsarten Eftersom reaktionshastigheten är proportionell mot andelen av reaktanten i övergångstillståndskomplexet, föreslogs enzymet för att öka koncentrationen av de reaktiva arterna.

Detta förslag formaliserades av Wolfenden och medarbetare vid University of North Carolina i Chapel Hill, som antog att hastighetsökningen som påtvingas av enzymer är proportionell mot enzymets affinitet för övergångstillståndsstrukturen i förhållande till Michaelis-komplexet. Eftersom enzymer vanligtvis ökar den icke-katalyserade reaktionshastigheten med faktorer på 10 ¹⁰ -10 ¹⁵ , och Michaelis-komplex ofta har dissociationskonstanter i intervallet 10 ⁻³ -10 ⁻⁶ M, föreslås det att övergångstillståndskomplex är bundna med dissociationskonstanter i intervallet 10 ⁻¹⁴ -10 ⁻²³ M. När substrat fortskrider från Michaelis-komplexet till produkt, uppstår kemi genom enzyminducerade förändringar i elektronfördelningen i substratet. Enzymer förändrar den elektroniska strukturen genom protonering, protonabstraktion, elektronöverföring, geometrisk distorsion, hydrofob uppdelning och interaktion med Lewis-syror och baser. Analoger som liknar övergångstillståndsstrukturerna bör därför tillhandahålla de mest kraftfulla icke-kovalenta inhibitorerna som är kända.

Alla kemiska omvandlingar passerar genom en instabil struktur som kallas övergångstillståndet, som är placerad mellan de kemiska strukturerna hos substraten och produkterna. Övergångstillstånden för kemiska reaktioner föreslås ha livstider nära 10-13 ^sekunder , i storleksordningen av tiden för en enkelbindningsvibration. Ingen fysisk eller spektroskopisk metod är tillgänglig för att direkt observera strukturen av övergångstillståndet för enzymatiska reaktioner, men övergångstillståndsstrukturen är central för att förstå enzymkatalys eftersom enzymer fungerar genom att sänka aktiveringsenergin för en kemisk transformation.

Det är nu accepterat att enzymer fungerar för att stabilisera övergångstillstånd som ligger mellan reaktanter och produkter, och att de därför skulle förväntas binda starkt till vilken hämmare som helst som nära liknar ett sådant övergångstillstånd. Substrat och produkter deltar ofta i flera enzymkatalyserade reaktioner, medan övergångstillståndet tenderar att vara karakteristiskt för ett speciellt enzym, så att en sådan inhibitor tenderar att vara specifik för det specifika enzymet. Identifieringen av många övergångstillståndshämmare stöder övergångstillståndsstabiliseringshypotesen för enzymatisk katalys.

För närvarande finns det ett stort antal enzymer kända för att interagera med övergångstillståndsanaloger, av vilka de flesta har utformats med avsikten att hämma målenzymet. Exempel inkluderar HIV-1-proteas, racemaser, β-laktamaser, metalloproteinaser, cyklooxygenaser och många andra.

Adsorption på ytor och reaktioner på ytor

Desorption såväl som reaktioner på ytor är enkla att beskriva med övergångstillståndsteori. Analys av adsorption till en yta från en flytande fas kan utgöra en utmaning på grund av bristande förmåga att bedöma koncentrationen av det lösta ämnet nära ytan. När fullständiga detaljer inte är tillgängliga, har det föreslagits att koncentrationer av reagerande arter ska normaliseras till koncentrationen av aktiva ytplatser, en approximation som kallas ytreaktant equi-density approximation (SREA).

Se även

• Curtin-Hammett-principen

Anteckningar

• Anslyn, Eric V.; Doughtery, Dennis A., Transition State Theory och relaterade ämnen. I Modern Physical Organic Chemistry University Science Books: 2006; sid 365-373
• Cleland, WW, Isotopeffekter: Bestämning av enzymövergångstillståndsstruktur. Methods in Enzymology 1995, 249, 341-373
• Laidler, K.; King, C., Utveckling av övergångstillståndsteori. The Journal of Physical Chemistry 1983, 87, (15), 2657
• Laidler, K., A lifetime of transition-state theory. The Chemical Intelligencer 1998, 4, (3), 39
• Radzicka, A.; Woldenden, R., Transition State and Multisubstrate$Analog Inhibitors. Methods in Enzymology 1995, 249, 284-312
• Schramm, VL., Enzymatic Transition States and Transition State Analog Design. Annual Review of Biochemistry 1998, 67, 693-720
• Schramm, VL, Enzymatic Transition State Theory och Transition State Analog Design. Journal of Biological Chemistry 2007, 282, (39), 28297-28300

externa länkar

• Enkel tillämpning av TST