Identitet (matematik)

Ej att förväxla med identitetselement , identitetsfunktion eller identitetsmatris .

Visuellt bevis för den pytagoreiska identiteten : för vilken vinkel som helst $\theta$ , punkten $(x,y)=(\cos \theta , \sin \theta )$ ligger på enhetscirkeln , som uppfyller ekvationen $x^{2}+y^{2}=1$ . Således är $\cos ^{2}\theta +\sin ^{2}\theta =1$ .

I matematik är en identitet en likhet som relaterar ett matematiskt uttryck A till ett annat matematiskt uttryck B , så att A och B (som kan innehålla vissa variabler ) producerar samma värde för alla värden av variablerna inom ett visst giltighetsintervall. Med andra ord, A = B är en identitet om A och B definierar samma funktioner , och en identitet är en likhet mellan funktioner som är olika definierade. Till exempel, $(a+b)^{2}=a^{2}+2ab+b^{2}$ och $\cos ^{2}\theta +\sin ^{2}\theta =1$ är identiteter. Identiteter indikeras ibland med trippelstapelsymbolen ≡ istället för = , likhetstecknet . Formellt är en identitet en universellt kvantifierad jämlikhet.

Gemensamma identiteter

Algebraiska identiteter

Se även: Faktorisering § Igenkännliga mönster

Vissa identiteter, som $a+0=a$ och $a+(-a)=0$ , utgör grunden för algebra , medan andra identiteter, som t.ex. $(a+b)^{2}=a^{2}+2ab+b^{2}$ och ${\displaystyle a^{2}-b^{2}=(a+b)(ab)} ,$ kan vara användbart för att förenkla algebraiska uttryck och utöka dem.

Trigonometriska identiteter

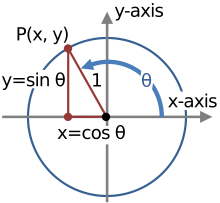
Huvudartikel: Lista över trigonometriska identiteter

Geometriskt är trigonometriska identiteter identiteter som involverar vissa funktioner av en eller flera vinklar . De skiljer sig från triangelidentiteter , som är identiteter som involverar både vinklar och sidolängder av en triangel . Endast de förra behandlas i denna artikel.

Dessa identiteter är användbara när uttryck som involverar trigonometriska funktioner behöver förenklas. En annan viktig tillämpning är integrationen av icke-trigonometriska funktioner: en vanlig teknik som innebär att man först använder substitutionsregeln med en trigonometrisk funktion och sedan förenklar den resulterande integralen med en trigonometrisk identitet.

Ett av de mest framträdande exemplen på trigonometriska identiteter involverar ekvationen $\sin ^{2}\theta +\cos ^{2}\theta =1,$ som är sant för alla reella värden på $\theta$ . Å andra sidan, ekvationen

$\cos \theta =1$

är bara sant för vissa värden på ${\displaystyle \theta } ,$ inte alla. Till exempel är denna ekvation sann när $\theta =0,$ men falsk när $\theta =2$ .

En annan grupp trigonometriska identiteter gäller de så kallade additions-/subtraktionsformlerna (t.ex. dubbelvinkelidentiteten $\sin(2\theta )=2\sin \ theta \cos \theta$ , additionsformeln för ${\displaystyle \tan(x+y)} ),$ som kan användas för att bryta ner uttryck för större vinklar till de med mindre beståndsdelar.

Exponentiella identiteter

Huvudartikel: Exponentiering

Följande identiteter gäller för alla heltalsexponenter , förutsatt att basen inte är noll:

${\begin{aligned}b^{m+n}&= b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b ^{n}\cdot c^{n}\end{aligned}}$

Till skillnad från addition och multiplikation är exponentiering inte kommutativ . Till exempel, 2 + 3 = 3 + 2 = 5 och 2 · 3 = 3 · 2 = 6 , men 2 ³ = 8 medan 3 ² = 9 .

Till skillnad från addition och multiplikation är exponentiering inte heller associativ . Till exempel, (2 + 3) + 4 = 2 + (3 + 4) = 9 och (2 · 3) · 4 = 2 · (3 · 4) = 24 , men 2 ³ till 4:an är 8 ⁴ (eller 4,096) medan 2 till 3 ⁴ är 2 ⁸¹ (eller 2,417,851,639,229,258,349,412,352). När inga parenteser skrivs är ordningen enligt konvention uppifrån och ner, inte nerifrån:

$b^{p^{q}}:=b^{(p^{q})},$ medan $(b^{p})^{q}=b^{p\cdot q}.$

Logaritmiska identiteter

Huvudartikel: Logaritmiska identiteter

Flera viktiga formler, ibland kallade logaritmiska identiteter eller loglagar , relaterar logaritmer till varandra:

Produkt, kvot, kraft och rot

En produkts logaritm är summan av logaritmerna för de tal som multipliceras; logaritmen för förhållandet mellan två tal är skillnaden mellan logaritmerna. Logaritmen för den p :te potensen av ett tal är p gånger logaritmen för själva talet; logaritmen för en p: te rot är logaritmen för talet dividerat med p . Följande tabell listar dessa identiteter med exempel. Var och en av identiteterna kan härledas efter substitution av logaritmdefinitionerna $x=b^{\log _{b}x},$ och/eller $y=b^{\log _{b}y},$ på vänster sida.

	Formel	Exempel
produkt	$\log _{b}(xy)=\log _{b}(x)+\log _{b} (y)$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5$
kvot	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)$	$\log _{2}(16)=\log _{ 2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
kraft	$\log _{b}(x^{p})=p\log _{b}(x)$	$\log _{2}(64)=\log _{2}(2^{6}) =6\log _{2}(2)=6$
rot	$\log _{b}\!{\sqrt[{p}]{x}}={\frac {\log _{b}(x)} {p}}$	$\log _{10}\!{\sqrt {1000}}={\frac {1}{2}}\log _{10} 1000={\frac {3}{2}}=1,5$

Byte av bas

Logaritmen log _b ( x ) kan beräknas från logaritmerna för x och b med avseende på en godtycklig bas k med hjälp av följande formel:

$\log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.$

Typiska vetenskapliga miniräknare beräknar logaritmerna till baserna 10 och e . Logaritmer med avseende på vilken bas b som helst kan bestämmas med någon av dessa två logaritmer med föregående formel:

$\log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e} (x)}{\log _{e}(b)}}.$

Givet ett tal x och dess logaritm log _b ( x ) till en okänd bas b , ges basen av:

$b=x^{\frac {1}{\log _{b}(x)}}.$

Hyperboliska funktionsidentiteter

Huvudartikel: Hyperbolisk funktion

De hyperboliska funktionerna tillfredsställer många identiteter, alla liknar de trigonometriska identiteterna i form . Faktum är att Osborns regel säger att man kan omvandla vilken trigonometrisk identitet som helst till en hyperbolisk identitet genom att expandera den helt i termer av heltalspotenser av sinus och cosinus, ändra sinus till sinh och cosinus till cosh och byta tecknet för varje term som innehåller en produkt av ett jämnt antal hyperboliska sinus.

Den Gudermannska funktionen ger ett direkt samband mellan de trigonometriska funktionerna och de hyperboliska som inte involverar komplexa tal .

Logik och universell algebra

Formellt är en identitet en sann universellt kvantifierad formel av formen $\forall x_{1},\ldots ,x_{n}:s=t,$ där s och t är termer utan andra fria variabler än $x_{1},\ldots ,x_{n}.$ Kvantifieringsprefixet $\forall x_{1},\ldots ,x_{n}$ lämnas ofta implicit , när det anges att formeln är en identitet. Till exempel ges ofta axiomen för en monoid som formler

$\forall x,y, z:x*(y*z)=(x*y)*z,\quad \forall x:x*1=x,\quad \forall x:1*x=x,$

eller, inom kort,

$x*(y*z)=(x*y)*z,\qquad x*1=x,\qquad 1*x=x.$

Så dessa formler är identiteter i varje monoid. Som för all likhet kallas formlerna utan kvantifierare ofta ekvationer . Med andra ord är en identitet en ekvation som är sann för alla värden på variablerna.

Se även

• Redovisningsidentitet
• Lista över matematiska identiteter

Källor

•   Downing, Douglas (2003). Algebra det enkla sättet . Barrons utbildningsserie. ISBN 978-0-7641-1972-9 .
•   Kate, SK; Bhapkar, HR (2009). Grunderna i matematik . Tekniska publikationer. ISBN 978-81-8431-755-8 .
•   Shirali, S. (2002). Äventyr i problemlösning . Universitetspressen. ISBN 978-81-7371-413-9 .

externa länkar

• The Encyclopedia of Equation Onlineuppslagsverk över matematiska identiteter (arkiverad)
• En samling algebraiska identiteter