Caesar chiffer
Inom kryptografi är ett Caesar-chiffer , även känt som Caesar's cipher , shift-chifferet , Caesar's code eller Caesar shift , en av de enklaste och mest kända krypteringsteknikerna . Det är en typ av substitutionschiffer där varje bokstav i klartexten ersätts av en bokstav något fast antal positioner ner i alfabetet . Till exempel, med ett vänsterskifte på 3, D ersättas med A , E skulle bli B , och så vidare. Metoden är uppkallad efter Julius Caesar , som använde den i sin privata korrespondens.
Krypteringssteget som utförs av ett Caesar-chiffer är ofta inkorporerat som en del av mer komplexa system, såsom Vigenère-chifferet , och har fortfarande modern tillämpning i ROT13 -systemet. Som med alla substitutionschiffer med ett alfabet, bryts Caesar-chifferet lätt och erbjuder i modern praktik i princip ingen kommunikationssäkerhet .
Exempel
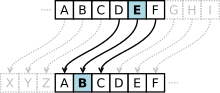
Transformationen kan representeras genom att ställa in två alfabet; chifferalfabetet är det vanliga alfabetet roterat åt vänster eller höger med ett antal positioner. Till exempel, här är ett Caesar-chiffer som använder en vänsterrotation på tre platser, vilket motsvarar ett högerskift på 23 (skiftparametern används som nyckel ) :
| Enkel | A | B | C | D | E | F | G | H | jag | J | K | L | M | N | O | P | F | R | S | T | U | V | W | X | Y | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chiffer | X | Y | Z | A | B | C | D | E | F | G | H | jag | J | K | L | M | N | O | P | F | R | S | T | U | V | W |
Vid kryptering slår en person upp varje bokstav i meddelandet i den "vanliga" raden och skriver ner motsvarande bokstav i "chiffer"-raden.
Klartext: DEN SNABBBRUNNA RÄVEN HOPPAR ÖVER DEN LATTA HUNDEN Chiffertext: QEB NRFZH YOLTK CLU GRJMP LSBO QEB IXWV ALD
Dechiffreringen görs omvänt, med en högerförskjutning på 3.
Krypteringen kan också representeras med hjälp av modulär aritmetik genom att först omvandla bokstäverna till siffror, enligt schemat, A → 0, B → 1, ..., Z → 25. Kryptering av en bokstav x med ett skift n kan beskrivas matematiskt som,
Dekryptering utförs på liknande sätt,
(Här hänvisar "mod" till modulo-operationen . Värdet x ligger i intervallet 0 till 25, men om x + n eller x − n inte är i detta intervall ska 26 adderas eller subtraheras.)
Ersättningen förblir densamma genom hela meddelandet, så chifferet klassas som en typ av monoalfabetisk substitution , i motsats till polyalfabetisk substitution .
Historia och användning

Caesar-chifferet är uppkallat efter Julius Caesar , som enligt Suetonius använde det med ett treskifte (A blir D vid kryptering och D blir A vid dekryptering) för att skydda meddelanden av militär betydelse. Medan Caesars var den första registrerade användningen av detta schema, är det känt att andra substitutionschiffer har använts tidigare.
"Om han hade något konfidentiellt att säga, skrev han det med chiffer, det vill säga genom att ändra ordningen på bokstäverna i alfabetet så att inte ett ord kunde urskiljas. Om någon vill dechiffrera dessa och komma till deras vilket betyder att han måste ersätta den fjärde bokstaven i alfabetet, nämligen D, med A, och så med de andra."
— Suetonius , Julius Caesars liv 56
Hans brorson, Augustus , använde också chiffret, men med ett högerskifte på ett, och det gick inte runt till början av alfabetet:
"När han skrev med chiffer skrev han B för A, C för B och resten av bokstäverna på samma princip, med AA för Z."
Det finns bevis för att Julius Caesar också använde mer komplicerade system, och en författare, Aulus Gellius , hänvisar till en (nu förlorad) avhandling om hans chiffer:
"Det finns till och med en ganska genialiskt skriven avhandling av grammatikern Probus angående bokstävernas hemliga betydelse i sammansättningen av Caesars epistlar."
— Aulus Gellius , Attic Nights 17.9.1–5
Det är okänt hur effektivt Caesar-chifferet var vid den tiden; det finns inga uppgifter vid den tidpunkten om några tekniker för lösning av enkla substitutionschiffer. Al-Kindis verk från 900-talet i arabvärlden med upptäckten av frekvensanalys .
Ett Caesar-chiffer med en förskjutning av ett används på baksidan av mezuzan för att kryptera Guds namn . Detta kan vara ett kvarhållande från en tidigare tid då judarna inte fick äta mezuzot. Bokstäverna i kryptogrammet utgör själva ett religiöst betydelsefullt "gudomligt namn" som ortodox tro håller ondskans krafter i schack.
På 1800-talet användes ibland avsnittet för personliga annonser i tidningar för att utbyta meddelanden krypterade med enkla chiffersystem. Kahn (1967) beskriver fall av älskare som ägnar sig åt hemlig kommunikation krypterad med hjälp av Caesar-chifferet i The Times . Ännu så sent som 1915 var Caesar-chifferet i bruk: den ryska armén använde det som en ersättning för mer komplicerade chiffer som hade visat sig vara för svåra för deras trupper att bemästra; Tyska och österrikiska kryptoanalytiker hade små svårigheter med att dekryptera sina meddelanden.
Caesar-chiffer finns idag i barnleksaker som hemliga dekoderringar . Ett Caesar-skift på tretton utförs också i ROT13 - algoritmen , en enkel metod för att fördunkla text som finns allmänt på Usenet och används för att dölja text (som skämtstämplar och berättelsespoilers), men som inte används på allvar som en krypteringsmetod.
Vigenère -chifferet använder ett Caesar-chiffer med olika förskjutningar vid varje position i texten; värdet på skiftet definieras med ett upprepande nyckelord. Om nyckelordet är lika långt som meddelandet, väljs slumpmässigt , aldrig blir känt för någon annan och aldrig återanvänds, är detta engångsblockchifferet, som har visat sig vara okrossbart. Förutsättningarna är så svåra att de i praktiken aldrig uppnås. Nyckelord som är kortare än meddelandet (t.ex. " Fullständig seger " som användes av konfederationen under det amerikanska inbördeskriget ) introducerar ett cykliskt mönster som kan upptäckas med en statistiskt avancerad version av frekvensanalys.
I april 2006 tillfångatogs den flyende maffiabossen Bernardo Provenzano på Sicilien , delvis på grund av att några av hans meddelanden, klumpigt skrivna i en variant av Caesar-chifferet, var trasiga. Provenzanos chiffer använde siffror, så att "A" skulle skrivas som "4", "B" som "5" och så vidare.
2011 dömdes Rajib Karim i Storbritannien för "terrorismbrott" efter att ha använt Caesar-chifferet för att kommunicera med bangladeshiska islamiska aktivister som diskuterade planer på att spränga British Airways- plan eller störa deras IT-nätverk. Även om parterna hade tillgång till mycket bättre krypteringstekniker (Karim använde själv PGP för datalagring på datordiskar), valde de att använda sitt eget schema (implementerat i Microsoft Excel ), och förkastade ett mer sofistikerat kodprogram som heter Mujahedeen Secrets " eftersom 'kaffirs' ', eller icke-troende, vet om det, så det måste vara mindre säkert".
Bryter chiffret
|
Dekrypteringsskifte _ |
Klartext kandidat |
|---|---|
| 0 | exexegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attack |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| ... | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
Caesar-chifferet kan lätt brytas även i ett scenario med enbart chiffertext . Två situationer kan övervägas:
- en angripare vet (eller gissar) att någon sorts enkel ersättnings-chiffer har använts, men inte specifikt att det är ett Caesar-schema;
- en angripare vet att ett Caesar-chiffer används, men vet inte skiftvärdet.
I det första fallet kan chifferet brytas med samma tekniker som för ett allmänt enkelt substitutionschiffer, såsom frekvensanalys eller mönsterord. Under lösningen är det troligt att en angripare snabbt kommer att märka regelbundenhet i lösningen och dra slutsatsen att ett Caesar-chiffer är den specifika algoritmen som används. [ citat behövs ]

I det andra fallet är det ännu enklare att bryta schemat. Eftersom det bara finns ett begränsat antal möjliga skift (25 på engelska) kan de var och en testas i tur och ordning i en brute force attack . Ett sätt att göra detta är att skriva ut ett stycke av chiffertexten i en tabell över alla möjliga skift – en teknik som ibland kallas "att fullborda den vanliga komponenten". Exemplet som ges är för chiffertexten " EXXEGOEXSRGI "; klartexten känns omedelbart igen [ vem? ] med ögat vid ett skift på fyra. Ett annat sätt att se den här metoden är att under varje bokstav i chiffertexten skrivs hela alfabetet omvänt med början på den bokstaven. Denna attack kan påskyndas med hjälp av en uppsättning remsor förberedda med alfabetet nedskrivet i omvänd ordning. Remsorna justeras sedan för att bilda chiffertexten längs en rad, och klartexten ska visas i en av de andra raderna. [ citat behövs ]
En annan brute force-strategi är att matcha frekvensfördelningen av bokstäverna. Genom att plotta bokstävernas frekvenser i chiffertexten, och genom att känna till den förväntade fördelningen av dessa bokstäver på originalspråket i klartexten, kan en människa lätt upptäcka värdet av förändringen genom att titta på förskjutningen av grafens speciella egenskaper. Detta är känt som frekvensanalys . Till exempel i det engelska språket är klartextfrekvenserna för bokstäverna E , T , (vanligtvis vanligast) och Q , Z (vanligtvis minst frekventa) särskilt distinkta. Datorer kan också göra detta genom att mäta hur väl den faktiska frekvensfördelningen stämmer överens med den förväntade fördelningen; till exempel chi-kvadratstatistiken användas.
För naturligt språk klartext kommer det vanligtvis bara att finnas en rimlig dekryptering, även om för extremt korta klartexter är flera kandidater möjliga. [ citat behövs ] Till exempel kan chiffertexten MPQY , troligtvis, dekryptera till antingen " aden " eller " vet " (förutsatt att klartexten är på engelska); på liknande sätt, " ALIIP " till " dockor " eller " hjul "; och " AFCCP " för att " joly " eller " heja " (se även unicity distans ).
Med Caesar-chifferet ger kryptering av en text flera gånger ingen extra säkerhet. Detta beror på att två krypteringar av, säg, skift A och skift B , kommer att vara ekvivalenta med en enda kryptering med skift A + B . I matematiska termer bildar uppsättningen av krypteringsoperationer under varje möjlig nyckel en grupp under sammansättning .
Se även
Anteckningar
Bibliografi
- Kahn, David (1996). The Codebreakers: The Story of Secret Writing (reviderad utgåva). New York. ISBN 0-684-83130-9 . OCLC 35159231 .
- Chris Savarese och Brian Hart, The Caesar Cipher , 1999
Vidare läsning
- Bauer, Friedrich Ludwig (2000). Decrypted Secrets: Methods and Maxims of Cryptology (andra och utökade upplagan). Berlin: Springer. ISBN 3-540-66871-3 . OCLC 43063275 .