Blockchiffer

Inom kryptografi är ett blockchiffer en deterministisk algoritm som arbetar på grupper med fast längd av bitar , kallade block . Blockchiffer är specificerade elementära komponenter i utformningen av många kryptografiska protokoll och används i stor utsträckning för att kryptera stora mängder data, inklusive i datautbytesprotokoll. Ett blockchiffer använder block som en oföränderlig transformation.

Även ett säkert blockchiffer är lämpligt för kryptering av endast ett enda datablock åt gången, med hjälp av en fast nyckel. Ett flertal driftsätt har utformats för att tillåta upprepad användning på ett säkert sätt för att uppnå säkerhetsmålen konfidentialitet och autenticitet . Emellertid kan blockchiffer också fungera som byggstenar i andra kryptografiska protokoll, såsom universella hashfunktioner och pseudoslumptalsgeneratorer .

Definition

Ett blockchiffer består av två parade algoritmer , en för kryptering, E , och den andra för dekryptering, D. Båda algoritmerna accepterar två ingångar: ett ingångsblock med storlek n bitar och en nyckel med storlek k bitar; och båda ger ett n -bitars utgångsblock. Dekrypteringsalgoritmen D definieras som den inversa funktionen av kryptering, dvs $D = E -1$ . Mer formellt specificeras ett blockchiffer av en krypteringsfunktion

E_{K}(P):=E(K,P) :\{0,1\}^{k}\ gånger \{0,1\}^{n}\högerpil \{0,1\}^{n},

som tar som indata en nyckel K , med bitlängd k (kallad nyckelstorlek ), och en bitsträng P , med längd n (kallad blockstorlek ), och returnerar en sträng C med n bitar. P kallas klartext och C kallas chiffertext . För varje K krävs att funktionen E _K ( P ) är en inverterbar mappning på ${0,1} n$ . Inversen för E definieras som en funktion

E_{K}^{- 1}(C):=D_{K}(C)=D(K,C):\{0,1\}^{k}\ gånger \{0,1\}^{n}\högerpil \{ 0,1\}^{n},

ta en nyckel K och en chiffertext C för att returnera ett klartextvärde P , så att

\forall P:D_{K}(E_{K}(P))=P.

Till exempel kan en blockchifferkrypteringsalgoritm ta ett 128-bitars block av klartext som indata och mata ut ett motsvarande 128-bitars block av chiffertext. Den exakta transformationen styrs med en andra ingång – den hemliga nyckeln. Dekryptering är liknande: dekrypteringsalgoritmen tar, i det här exemplet, ett 128-bitars block av chiffertext tillsammans med den hemliga nyckeln, och ger det ursprungliga 128-bitars blocket med vanlig text.

För varje nyckel K är EK _. en permutation (en bijektiv mappning) över uppsättningen av ingångsblock Varje tangent väljer en permutation från uppsättningen av $(2^{n})!$ möjliga permutationer.

Historia

Den moderna designen av blockchiffer är baserad på konceptet med ett itererat produktchiffer . I sin framstående publikation från 1949, Communication Theory of Secrecy Systems, analyserade Claude Shannon produktchiffer och föreslog dem som ett sätt att effektivt förbättra säkerheten genom att kombinera enkla operationer som substitutioner och permutationer . Itererade produktchiffer utför kryptering i flera omgångar, som var och en använder en annan undernyckel härledd från den ursprungliga nyckeln. En utbredd implementering av sådana chiffer som heter ett Feistel-nätverk efter Horst Feistel är särskilt implementerat i DES -chifferet. Många andra realiseringar av blockchiffer, såsom AES , klassificeras som substitutions-permutationsnätverk .

Roten till alla kryptografiska blockformat som används inom standarderna Payment Card Industry Data Security Standard (PCI DSS) och American National Standards Institute (ANSI) ligger i Atalla Key Block (AKB), som var en nyckelinnovation av Atalla Box , första hårdvarusäkerhetsmodulen (HSM). Den utvecklades 1972 av Mohamed M. Atalla , grundare av Atalla Corporation (numera Utimaco Atalla ), och släpptes 1973. AKB var ett nyckelblock som krävs för att säkert utbyta symmetriska nycklar eller PIN-koder med andra aktörer inom banksektorn . Detta säkra utbyte utförs med AKB-formatet. Atalla Box skyddade över 90 % av alla ATM- nätverk i drift från 1998, och Atalla-produkter säkrar fortfarande majoriteten av världens ATM-transaktioner från och med 2014.

Publiceringen av DES-chifferet av United States National Bureau of Standards (senare US National Institute of Standards and Technology, NIST) 1977 var grundläggande för allmänhetens förståelse av modern blockchifferdesign. Det påverkade också den akademiska utvecklingen av kryptoanalytiska attacker . Både differentiell och linjär kryptoanalys uppstod ur studier om DES-design. Från och med 2016 finns det en palett av attacktekniker mot vilka ett blockchiffer måste vara säkert, förutom att vara robust mot brute-force-attacker .

Design

Itererade blockchiffer

De flesta blockchifferalgoritmer klassificeras som itererade blockchiffer , vilket innebär att de omvandlar block av klartext av fast storlek till block av chiffertext av samma storlek , via den upprepade tillämpningen av en inverterbar transformation känd som den runda funktionen , med varje iteration som kallas en runda .

tar den runda funktionen R olika runda tangenter K _i som en andra ingång, som härleds från den ursprungliga nyckeln: ^{[ citat behövs ]}

M_{i}=R_{K_{i}}(M_{i-1})

där $M_{0}$ är klartexten och $M_{r}$ chiffertexten, där r är antalet omgångar.

Utöver detta används ofta nyckelblekning . I början och slutet modifieras data med nyckelmaterial (ofta med XOR , men enkla aritmetiska operationer som att addera och subtrahera används också): ^{[ citat behövs ]}

M_{0}=M\oplus K_{0}

M_{i}=R_{K_{i}}(M_{i-1})\;;\;i=1\prickar r

C=M_{r}\oplus K_{r+1}

Med tanke på ett av de vanliga itererade blockchifferdesignschemana är det ganska enkelt att konstruera ett blockchiffer som är kryptografiskt säkert, helt enkelt genom att använda ett stort antal omgångar. Detta kommer dock att göra chifferet ineffektivt. Effektivitet är således det viktigaste ytterligare designkriteriet för professionella chiffer. Vidare är ett bra blockchiffer designat för att undvika sidokanalattacker, såsom grenprediktion och ingångsberoende minnesåtkomster som kan läcka hemlig data via cachetillståndet eller exekveringstiden. Dessutom bör chiffret vara kortfattat för små hårdvaru- och mjukvaruimplementationer. Slutligen bör chifferet vara lätt kryptanalyserbart, så att det kan visas hur många omgångar chifferet behöver reduceras till för att de befintliga kryptografiska attackerna skulle fungera – och omvänt att det kan visas att antalet faktiska rundor är tillräckligt stor för att skydda mot dem. ^{[ citat behövs ]}

Substitution-permutationsnätverk

En skiss av ett substitutions-permutationsnätverk med 3 omgångar, krypterar ett klartextblock på 16 bitar till ett chiffertextblock på 16 bitar. S-rutorna är Si _är , P-rutorna är samma P och de runda nycklarna K _i .

En viktig typ av itererat blockchiffer känd som ett substitutions-permutationsnätverk (SPN) tar ett block av klartexten och nyckeln som indata och tillämpar flera alternerande omgångar bestående av ett substitutionssteg följt av ett permutationssteg - för att producera varje block av chiffertext produktion. Det icke-linjära substitutionssteget blandar nyckelbitarna med de i klartexten, vilket skapar Shannons förvirring . Det linjära permutationssteget skingrar sedan redundanser och skapar diffusion .

En substitutionsbox (S-box) ersätter ett litet block av ingångsbitar med ett annat block av utbitar. Denna ersättning måste vara en-till-en för att säkerställa inverterbarhet (därav dekryptering). En säker S-box kommer att ha egenskapen att en ändring av en ingångsbit kommer att ändra ungefär hälften av utgångsbitarna i genomsnitt, uppvisar vad som kallas lavineffekten — dvs den har egenskapen att varje utgångsbit kommer att bero på varje ingångsbit.

En permutationsbox (P-box) är en permutation av alla bitar: den tar utdata från alla S-boxar i en omgång, permuterar bitarna och matar in dem i S-boxarna i nästa omgång. En bra P-box har egenskapen att utgångsbitarna från vilken S-box som helst distribueras till så många S-box-ingångar som möjligt. ^{[ citat behövs ]}

Vid varje runda kombineras rundtangenten (erhållen från nyckeln med några enkla operationer, till exempel med S-boxar och P-boxar) med hjälp av någon gruppoperation, typiskt XOR . ^{[ citat behövs ]}

Dekryptering görs genom att helt enkelt vända processen (använda inverserna av S-boxarna och P-boxarna och använda de runda nycklarna i omvänd ordning).

Feistel chiffer

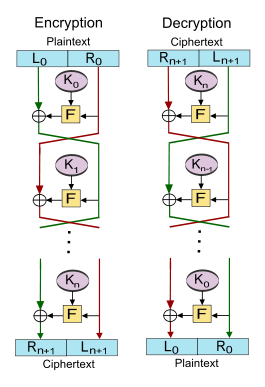
Många blockchiffer, som DES och Blowfish använder strukturer som kallas Feistel-chiffer

I ett Feistel-chiffer är blocket med vanlig text som ska krypteras uppdelat i två lika stora halvor. Den runda funktionen appliceras på ena halvan med hjälp av en undernyckel, och sedan XOReds utdata med den andra halvan. De två halvorna byts sedan om.

Låt ${\rm {F}}$ vara den runda funktionen och låt $K_{0},K_{1},\ldots ,K_{n}$ vara undernycklarna för rundorna $0,1,\ldots ,n$ respektive.

Då är den grundläggande operationen som följer:

Dela klartextblocket i två lika stora delar, ( $L_{0}$ , $R_{0}$ )

För varje omgång $i=0,1,\dots ,n$ , beräkna

L_{i+1}=R_{i}\,

\displaystyle R_{i+1}= L_{i}\oplus {\rm {F}}(R_{i},K_{i})}

.

Då är chiffertexten $(R_{n+1},L_{n+1})$ .

Dekrypteringen av en chiffertext $(R_{n+1},L_{n+1})$ åstadkommes genom att beräkna $i=n,n-1,\ldots ,0$

\displaystyle R_{i}=L_{i+1}\,}

L_{i}= R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})

.

Sedan är $(L_{0},R_{0})$ klartext igen.

En fördel med Feistel-modellen jämfört med ett substitutions-permutationsnätverk är att den runda funktionen ${\rm {F}}$ inte behöver vara inverterbar.

Lai–Massey chiffer

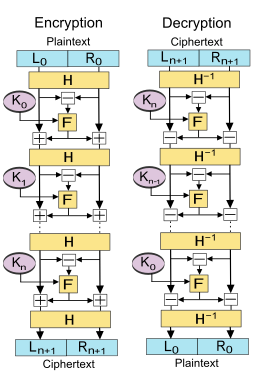
Lai–Massey-schemat. Det arketypiska chiffer som använder det är IDEA .

Lai-Massey-schemat erbjuder säkerhetsegenskaper som liknar Feistel-strukturen . Det delar också fördelen att den runda funktionen $\mathrm {F}$ inte behöver vara inverterbar. En annan likhet är att den också delar upp inmatningsblocket i två lika stora delar. Men den runda funktionen tillämpas på skillnaden mellan de två, och resultatet läggs sedan till båda halvblocken.

Låt $\mathrm {F}$ vara den runda funktionen och $\mathrm {H}$ en halvrunda funktion och låt $K_{0}, K_{1},\ldots ,K_{n}$ är undernycklarna för rundorna $0,1,\ldots ,n$ respektive.

Då är den grundläggande operationen som följer:

Dela klartextblocket i två lika stora delar, ( $L_{0}$ , $R_{0}$ )

För varje omgång $i=0,1,\dots ,n$ , beräkna

(L_{i+1}',R_{i+1

där $T_{i}=\mathrm {F} (L_{i}'-R_{i}',K_{i})$ och $(L_{0}',R_{0}')=\mathrm {H} (L_{0},R_{0})$

Då är chiffertexten $(L_{n+1},R_{n+1})=(L_ {n+1}',R_{n+1}')$ .

Dekrypteringen av en chiffertext $(L_{n+1},R_{n+1})$ åstadkommes genom att beräkna $i=n,n-1,\ldots ,0$

\displaystyle (L_{i}',R_{i}')=

där $T_{i}=\mathrm {F} (L_{i+1}'-R_{i+1$ och $\displaystyle (L_{n+1}'$

Då är $(L_{0},R_{0})=(L_{0}',R_{0}')$ klartext igen.

Operationer

ARX (lägg till – rotera – XOR)

Många moderna blockchiffer och hash är ARX- algoritmer – deras runda funktion involverar bara tre operationer: (A) modulär addition, (R) rotation med fasta rotationsmängder och (X) XOR . Exempel inkluderar ChaCha20 , Speck , XXTEA och BLAKE . Många författare ritar ett ARX-nätverk, ett slags dataflödesdiagram , för att illustrera en sådan rund funktion.

Dessa ARX-operationer är populära eftersom de är relativt snabba och billiga i hårdvara och mjukvara, deras implementering kan göras extremt enkel, och även för att de körs i konstant tid och därför är immuna mot tajmingsattacker . Den roterande kryptoanalystekniken försöker attackera sådana runda funktioner.

Övriga operationer

Andra operationer som ofta används i blockchiffer inkluderar databeroende rotationer som i RC5 och RC6 , en ersättningsbox implementerad som en uppslagstabell som i Data Encryption Standard och Advanced Encryption Standard , en permutationsbox och multiplikation som i IDEA .

Driftsätt

Osäker kryptering av en bild som ett resultat av kodning i elektronisk kodbok (ECB).

Ett blockchiffer i sig tillåter endast kryptering av ett enda datablock av chifferets blocklängd. För ett meddelande med variabel längd måste data först delas upp i separata chifferblock. I det enklaste fallet, känt som elektronisk kodbok (ECB), delas ett meddelande först upp i separata block av chifferets blockstorlek (möjligen utökar det sista blocket med utfyllnadsbitar ), och sedan krypteras och dekrypteras varje block oberoende av varandra. En sådan naiv metod är dock i allmänhet osäker eftersom lika klartextblock alltid genererar lika chiffertextblock (för samma nyckel), så mönster i klartextmeddelandet blir tydliga i chiffertextutmatningen.

För att övervinna denna begränsning har flera så kallade blockchifferfunktioner designats och specificerats i nationella rekommendationer som NIST 800-38A och BSI TR-02102 och internationella standarder som ISO/IEC 10116 . Det allmänna konceptet är att använda randomisering av klartextdata baserat på ett extra inmatningsvärde, ofta kallat en initialiseringsvektor , för att skapa vad som kallas probabilistisk kryptering . I det populära chifferblockkedjningsläget (CBC), för att kryptering ska vara säker måste initialiseringsvektorn som skickas tillsammans med klartextmeddelandet vara ett slumpmässigt eller pseudoslumpmässigt värde, som läggs till på ett exklusivt eller sätt till det första klartextblocket före den är krypterad. Det resulterande chiffertextblocket används sedan som den nya initialiseringsvektorn för nästa klartextblock. I chifferåterkopplingsläget (CFB), som emulerar ett självsynkroniserande strömchiffer , krypteras initialiseringsvektorn först och läggs sedan till i klartextblocket. Utmatningsåterkopplingsläget (OFB) krypterar upprepade gånger initieringsvektorn för att skapa en nyckelström för emulering av ett synkront strömchiffer . Det nyare räknarläget (CTR) skapar på liknande sätt en nyckelström, men har fördelen av att endast behöva unika och inte (pseudo-)slumpmässiga värden som initialiseringsvektorer; den nödvändiga slumpen härleds internt genom att använda initialiseringsvektorn som en blockräknare och kryptera denna räknare för varje block.

Ur en säkerhetsteoretisk synvinkel måste driftsätt ge det som kallas semantisk säkerhet . Informellt betyder det att man givet en viss chiffertext under en okänd nyckel praktiskt taget inte kan härleda någon information från chiffertexten (annat än meddelandets längd) över vad man skulle ha vetat utan att ha sett chiffertexten. Det har visat sig att alla de metoder som diskuterats ovan, med undantag för ECB-läget, tillhandahåller denna egenskap under så kallade vald klartext-attacker .

Stoppning

Vissa lägen som CBC-läget fungerar bara på kompletta klartextblock. Att helt enkelt utöka det sista blocket i ett meddelande med noll bitar är otillräckligt eftersom det inte tillåter en mottagare att enkelt särskilja meddelanden som bara skiljer sig i antalet utfyllnadsbitar. Ännu viktigare, en så enkel lösning ger upphov till mycket effektiva utfyllnads-orakelattacker . Ett lämpligt utfyllnadsschema behövs därför för att utöka det sista klartextblocket till chifferets blockstorlek. Medan många populära system som beskrivs i standarder och i litteraturen har visat sig vara sårbara för utfyllnad av orakelattacker, är en lösning som lägger till en enbit och sedan utökar det sista blocket med nollbitar, standardiserad som "utfyllnadsmetod 2" i ISO /IEC 9797-1, har visat sig vara säker mot dessa attacker.

Kryptanalys

Brute-force attacker

Denna egenskap resulterar i att chifferns säkerhet försämras kvadratiskt och måste tas med i beräkningen när du väljer en blockstorlek. Det finns dock en avvägning eftersom stora blockstorlekar kan resultera i att algoritmen blir ineffektiv att använda. Tidigare blockchiffer som DES har vanligtvis valt en 64-bitars blockstorlek, medan nyare design som AES stödjer blockstorlekar på 128 bitar eller mer, med vissa chiffer som stöder en rad olika blockstorlekar.

Differentiell kryptoanalys

Linjär kryptoanalys

En linjär kryptoanalys är en form av kryptoanalys som bygger på att hitta affina approximationer till ett chiffers verkan . Linjär kryptoanalys är en av de två mest använda attackerna på blockchiffer; den andra är differentiell kryptoanalys .

Upptäckten tillskrivs Mitsuru Matsui , som först tillämpade tekniken på FEAL- chifferet (Matsui och Yamagishi, 1992).

Integral kryptoanalys

Integral kryptoanalys är en kryptoanalytisk attack som är särskilt användbar för att blockera chiffer baserade på substitution-permutationsnätverk. Till skillnad från differentiell kryptoanalys, som använder par av utvalda klartexter med en fast XOR-skillnad, använder integrerad kryptoanalys uppsättningar eller till och med multiuppsättningar av utvalda klartexter av vilka en del hålls konstant och en annan del varierar genom alla möjligheter. Till exempel kan en attack använda 256 utvalda klartexter som har alla utom 8 bitar lika, men alla skiljer sig i dessa 8 bitar. En sådan uppsättning har nödvändigtvis en XOR-summa på 0, och XOR-summorna för motsvarande uppsättningar av chiffertexter ger information om chifferns funktion. Denna kontrast mellan skillnaderna mellan par av texter och summorna av större uppsättningar texter inspirerade namnet "integral kryptoanalys", som lånade terminologin för kalkyl. ^{[ citat behövs ]}

Andra tekniker

Utvecklingen av bumerangattacken gjorde det möjligt för differentiell kryptoanalys att tillämpas på många chiffer som tidigare ansetts säkra mot differentiella attacker

Förutom linjär och differentiell kryptoanalys, finns det en växande katalog av attacker: trunkerad differentiell kryptoanalys , partiell differentiell kryptoanalys, integral kryptoanalys , som omfattar kvadratiska och integrerade attacker, glidattacker , bumerangattacker , XSL -attacken , omöjlig differentiell kryptoanalys och algebra. attacker. För att en ny blockchifferdesign ska ha någon trovärdighet måste den visa bevis på säkerhet mot kända attacker. ^{[ citat behövs ]}

Bevisbar säkerhet

När ett blockchiffer används i ett givet funktionssätt bör den resulterande algoritmen helst vara ungefär lika säker som själva blockchifferet. ECB (diskuterat ovan) saknar med eftertryck denna egenskap: oavsett hur säkert det underliggande blockchifferet är, kan ECB-läget lätt attackeras. Å andra sidan kan CBC-läge bevisas vara säkert under antagandet att det underliggande blockchifferet också är säkert. Observera dock att att göra påståenden som detta kräver formella matematiska definitioner för vad det betyder att en krypteringsalgoritm eller ett blockchiffer ska "vara säkert". Det här avsnittet beskriver två vanliga föreställningar om vilka egenskaper ett blockchiffer ska ha. Var och en motsvarar en matematisk modell som kan användas för att bevisa egenskaper hos högre nivåalgoritmer, såsom CBC.

Detta allmänna tillvägagångssätt för kryptografi – vilket bevisar att algoritmer på högre nivå (som CBC) är säkra under explicit angivna antaganden om deras komponenter (som ett blockchiffer) – är känt som bevisbar säkerhet .

Standardmodell

Informellt sett är ett blockchiffer säkert i standardmodellen om en angripare inte kan se skillnaden mellan blockchifferet (utrustat med en slumpmässig nyckel) och en slumpmässig permutation.

För att vara lite mer exakt, låt E vara ett n -bitars blockchiffer. Vi föreställer oss följande spel:

Personen som driver spelet slår ett mynt.
- Om myntet landar på huvuden väljer han en slumpmässig nyckel K och definierar funktionen f = E _K .
- Om myntet landar på svansar, väljer han en slumpmässig permutation $π$ på uppsättningen av n -bitars strängar och definierar funktionen f = $π$ .
Angriparen väljer en n -bitars sträng X , och personen som kör spelet berättar för honom värdet av f ( X ).
Steg 2 upprepas totalt q gånger. (Var och en av dessa q -interaktioner är en fråga .)
Angriparen gissar hur myntet landade. Han vinner om hans gissning är korrekt.

Angriparen, som vi kan modellera som en algoritm, kallas en motståndare . Funktionen f (som motståndaren kunde fråga) kallas ett orakel .

Observera att en motståndare trivialt kan säkerställa en 50% chans att vinna genom att bara gissa slumpmässigt (eller till och med genom att till exempel alltid gissa "huvuden"). Låt därför P _E ( A ) beteckna sannolikheten att motståndare A vinner detta spel mot E , och definiera fördelen med A som 2( P _E ( A ) − 1/2). Det följer att om A gissar slumpmässigt kommer dess fördel att vara 0; å andra sidan, om A alltid vinner, är dess fördel 1. Blockchifferet E är en pseudo-slumpmässig permutation (PRP) om ingen motståndare har en fördel som är betydligt större än 0, givet specificerade begränsningar för q och motståndarens speltid . Om motståndare i steg 2 ovan har möjligheten att lära sig f ⁻¹ ( X ) istället för f ( X ) (men fortfarande bara har små fördelar) så är E en stark PRP (SPRP). En motståndare är icke-adaptiv om den väljer alla q -värden för X innan spelet börjar (det vill säga att den inte använder någon information från tidigare frågor för att välja varje X allt eftersom).

Dessa definitioner har visat sig användbara för att analysera olika driftsätt. Till exempel kan man definiera ett liknande spel för att mäta säkerheten för en blockchifferbaserad krypteringsalgoritm, och sedan försöka visa (genom ett reduktionsargument ) att sannolikheten för att en motståndare vinner detta nya spel inte är mycket mer än P _E ( A ) för vissa A. (Reduktionen ger vanligtvis gränser för q och körtiden för A .) På motsvarande sätt, om P _E ( A ) är liten för alla relevanta A , har ingen angripare en betydande sannolikhet att vinna det nya spelet. Detta formaliserar tanken att algoritmen på högre nivå ärver blockchifferets säkerhet.

Idealisk chiffermodell

Praktisk utvärdering

Blockchiffer kan utvärderas enligt flera kriterier i praktiken. Vanliga faktorer inkluderar:

Nyckelparametrar, som dess nyckelstorlek och blockstorlek, som båda ger en övre gräns för chifferns säkerhet.
Den uppskattade säkerhetsnivån , som är baserad på det förtroende som fåtts för blockchifferdesignen efter att den i stort sett har stått emot stora ansträngningar inom kryptoanalys över tid, designens matematiska sundhet och förekomsten av praktiska eller certifierade attacker.
Chifferens komplexitet och dess lämplighet för implementering i hårdvara eller mjukvara . Hårdvaruimplementationer kan mäta komplexiteten i termer av grindantal eller energiförbrukning, vilket är viktiga parametrar för resursbegränsade enheter.
Chifferens prestanda när det gäller bearbetningsgenomströmning på olika plattformar, inklusive dess minneskrav .
Kostnaden för chifferet avser licenskrav som kan gälla på grund av immateriella rättigheter .
Cifferens flexibilitet inkluderar dess förmåga att stödja flera nyckelstorlekar och blocklängder .

Anmärkningsvärda blockchiffer

Lucifer / DES

Lucifer anses allmänt vara det första civila blockchifferet, utvecklat på IBM på 1970-talet baserat på arbete utfört av Horst Feistel . En reviderad version av algoritmen antogs som en amerikansk statlig federal informationsbehandlingsstandard : FIPS PUB 46 Data Encryption Standard (DES). Det valdes av US National Bureau of Standards (NBS) efter en offentlig inbjudan till inlämningar och några interna ändringar av NBS (och eventuellt NSA ). DES släpptes offentligt 1976 och har använts flitigt. ^{[ citat behövs ]}

DES designades för att bland annat motstå en viss kryptoanalytisk attack känd av NSA och återupptäckt av IBM, dock okänd offentligt tills den återupptäcktes igen och publicerades av Eli Biham och Adi Shamir i slutet av 1980-talet. Tekniken kallas differentiell kryptoanalys och är fortfarande en av få allmänna attacker mot blockchiffer; linjär kryptoanalys är en annan men kan ha varit okänd även för NSA, innan den publicerades av Mitsuru Matsui . DES föranledde en stor mängd annat arbete och publikationer inom kryptografi och kryptoanalys i det öppna samhället och det inspirerade många nya chifferdesigner. ^{[ citat behövs ]}

DES har en blockstorlek på 64 bitar och en nyckelstorlek på 56 bitar. 64-bitars block blev vanliga i blockchifferdesigner efter DES. Nyckellängden berodde på flera faktorer, inklusive statlig reglering. Många observatörer ^{[ vem? ]} på 1970-talet kommenterade att nyckellängden på 56 bitar som användes för DES var för kort. Allt eftersom tiden gick blev dess otillräcklighet uppenbar, särskilt efter att en specialmaskin designad för att bryta DES demonstrerades 1998 av Electronic Frontier Foundation . En tillägg till DES, Triple DES , trippelkrypterar varje block med antingen två oberoende nycklar (112-bitars nyckel och 80-bitars säkerhet) eller tre oberoende nycklar (168-bitars nyckel och 112-bitars säkerhet). Det antogs allmänt som en ersättning. Från och med 2011 anses versionen med tre nycklar fortfarande vara säker, även om från National Institute of Standards and Technology (NIST) inte längre tillåter användning av tvånyckelversionen i nya applikationer, på grund av dess 80-bitars säkerhetsnivå.

ANING

International Data Encryption Algorithm ( IDEA ) är ett blockchiffer designat av James Massey från ETH Zürich och Xuejia Lai ; den beskrevs först 1991, som en avsedd ersättning för DES.

IDEA fungerar på 64-bitars block med en 128-bitars nyckel och består av en serie av åtta identiska transformationer (en runda ) och en utgående transformation (halvrundan ) . Processerna för kryptering och dekryptering är liknande. IDEA hämtar mycket av sin säkerhet genom att interfoliera operationer från olika grupper – modulär addition och multiplikation, och bitvis exklusiv eller (XOR) – som är algebraiskt "inkompatibla" i någon mening.

Designerna analyserade IDEA för att mäta dess styrka mot differentiell kryptoanalys och drog slutsatsen att den är immun under vissa antaganden. Inga framgångsrika linjära eller algebraiska svagheter har rapporterats. Från och med 2012 kan den bästa attacken som gäller alla nycklar bryta en hel 8,5-runda IDEA med en smal-bicliques attack ungefär fyra gånger snabbare än brute force.

RC5

En omgång (två halvomgångar) av RC5-blockchifferet

RC5 är ett blockchiffer designat av Ronald Rivest 1994 som, till skillnad från många andra chiffer, har en variabel blockstorlek (32, 64 eller 128 bitar), nyckelstorlek (0 till 2040 bitar) och ett antal rundor (0 till 255). Det ursprungliga föreslagna valet av parametrar var en blockstorlek på 64 bitar, en 128-bitars nyckel och 12 rundor.

En nyckelfunktion hos RC5 är användningen av databeroende rotationer; ett av målen med RC5 var att få till stånd studier och utvärdering av sådana operationer som en kryptografisk primitiv. RC5 består också av ett antal modulära tillägg och XOR. Algoritmens allmänna struktur är ett Feistel- liknande nätverk. Krypterings- och dekrypteringsrutinerna kan specificeras i några rader kod. Nyckelschemat är dock mer komplext och utökar nyckeln med en i huvudsak envägsfunktion med de binära expansionerna av både e och det gyllene snittet som källor till " ingenting i rockärmen" . Algoritmens lockande enkelhet tillsammans med nyheten i de databeroende rotationerna har gjort RC5 till ett attraktivt studieobjekt för kryptoanalytiker.

12-runda RC5 (med 64-bitars block) är mottaglig för en differentiell attack med 2 ⁴⁴ valda klartexter. 18–20 omgångar föreslås som tillräckligt skydd.

Rijndael / AES

Rijndael - chifferet utvecklat av belgiska kryptografer, Joan Daemen och Vincent Rijmen var en av de konkurrerande designerna för att ersätta DES. Den vann den 5-åriga offentliga tävlingen för att bli AES, (Advanced Encryption Standard).

AES antogs av NIST 2001 och har en fast blockstorlek på 128 bitar och en nyckelstorlek på 128, 192 eller 256 bitar, medan Rijndael kan specificeras med block- och nyckelstorlekar i valfri multipel av 32 bitar, med ett minimum av 128 bitar. Blockstorleken har maximalt 256 bitar, men nyckelstorleken har inget teoretiskt maximum. AES opererar på en 4×4 kolumnstor beställningsmatris av bytes, kallad staten (versioner av Rijndael med en större blockstorlek har ytterligare kolumner i staten).

blåsfisk

Blowfish är ett blockchiffer, designat 1993 av Bruce Schneier och ingår i ett stort antal chiffersviter och krypteringsprodukter. Blowfish har en 64-bitars blockstorlek och en variabel nyckellängd från 1 bit upp till 448 bitar. Det är ett 16-rundt Feistel-chiffer och använder stora nyckelberoende S-boxar . Anmärkningsvärda funktioner i designen inkluderar de nyckelberoende S-boxarna och ett mycket komplext nyckelschema .

Den designades som en allmän algoritm, avsedd som ett alternativ till den åldrande DES och fri från de problem och begränsningar som är förknippade med andra algoritmer. När Blowfish släpptes var många andra mönster patentskyddade, eller var kommersiella/statliga hemligheter. Schneier har sagt att "Blowfish är opatenterat och kommer att förbli så i alla länder. Algoritmen placeras härmed i det offentliga området och kan fritt användas av vem som helst." Detsamma gäller Twofish , en efterföljande algoritm från Schneier.

Generaliseringar

Tweakbara blockchiffer

M. Liskov, R. Rivest och D. Wagner har beskrivit en generaliserad version av blockchiffer som kallas "tweakable" blockchiffer. Ett tweakbart blockchiffer accepterar en andra inmatning som kallas tweaken tillsammans med dess vanliga klartext eller chiffertextinmatning. Tweaken, tillsammans med nyckeln, väljer permutationen som beräknas av chiffret. Om ändring av tweaks är tillräckligt lätt (jämfört med en vanligtvis ganska dyr tangentinställning), blir några intressanta nya driftlägen möjliga. om diskkrypteringsteori beskriver några av dessa lägen.

Formatbevarande kryptering

Blockchiffer fungerar traditionellt över ett binärt alfabet . Det vill säga både ingången och utgången är binära strängar, bestående av n nollor och ettor. I vissa situationer kan man dock önska att ha ett blockchiffer som fungerar över något annat alfabet; till exempel, kryptering av 16-siffriga kreditkortsnummer på ett sådant sätt att chiffertexten också är ett 16-siffrigt nummer kan underlätta att lägga till ett krypteringslager till äldre programvara. Detta är ett exempel på formatbevarande kryptering . Mer generellt kräver formatbevarande kryptering en nyckelad permutation på något ändligt språk . Detta gör formatbevarande krypteringsscheman till en naturlig generalisering av (tweakbara) blockchiffer. Däremot är traditionella krypteringsscheman, såsom CBC, inte permutationer eftersom samma klartext kan kryptera flera olika chiffertexter, även när man använder en fast nyckel.

Relation till andra kryptografiska primitiver

Blockchiffer kan användas för att bygga andra kryptografiska primitiver, som de nedan. För att dessa andra primitiver ska vara kryptografiskt säkra måste man vara noga med att bygga dem på rätt sätt.

Strömchiffer kan byggas med blockchiffer. OFB-läge och CTR-läge är blocklägen som förvandlar ett blockchiffer till ett strömchiffer.
Kryptografiska hashfunktioner kan byggas med blockchiffer. Se envägskomprimeringsfunktionen för beskrivningar av flera sådana metoder. Metoderna liknar de blockchifferfunktioner som vanligtvis används för kryptering.
Kryptografiskt säkra pseudoslumptalsgeneratorer (CSPRNG) kan byggas med hjälp av blockchiffer.
Säkra pseudoslumpmässiga permutationer av ändliga mängder av godtycklig storlek kan konstrueras med blockchiffer; se Formatbevarande kryptering .
En allmänt känd oförutsägbar permutation i kombination med nyckelblekning räcker för att konstruera ett blockchiffer - som t.ex. Even-Mansour-chifferet med en nyckel, kanske det enklaste möjliga bevisligen säkra blockchifferet.
Meddelandeautentiseringskoder (MAC) är ofta byggda från blockchiffer. CBC-MAC , OMAC och PMAC är sådana MAC.
Autentiserad kryptering är också byggd från blockchiffer. Det innebär att både kryptera och MAC samtidigt. Det är att både tillhandahålla konfidentialitet och autentisering . CCM , EAX , GCM och OCB är sådana autentiserade krypteringslägen.

Precis som blockchiffer kan användas för att bygga hashfunktioner, som SHA-1 och SHA-2 är baserade på blockchiffer som också används oberoende som SHACAL , kan hashfunktioner användas för att bygga blockchiffer. Exempel på sådana blockchiffer är BEAR och LION .

Se även

Vidare läsning

Knudsen, Lars R.; Robshaw, Matthew (2011). Block Chiffer Companion . Springer. ISBN 9783642173417 .

externa länkar