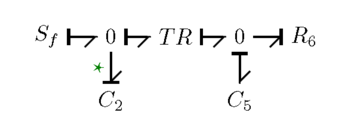Bond graf

Den här artikeln handlar om grafer som representerar utbyten av fysisk energi. För multigrafer med två vertex, se dipoldiagram .

Ett enkelt mass-fjäder-dämparsystem och dess ekvivalenta bindningsgrafform

En obligationsgraf är en grafisk representation av ett fysiskt dynamiskt system . Det tillåter omvandling av systemet till en representation av tillståndsutrymme . Det liknar ett blockdiagram eller signalflödesdiagram , med den stora skillnaden att bågarna i bindningsdiagram representerar dubbelriktat utbyte av fysisk energi , medan de i blockdiagram och signalflödesdiagram representerar enkelriktat informationsflöde. Bond-grafer är flerenergidomän (t.ex. mekanisk, elektrisk, hydraulisk, etc.) och domänneutral. Detta innebär att en obligationsgraf kan integrera flera domäner sömlöst.

Bond-grafen är sammansatt av "bonds" som länkar samman "single-port", "double-port" och "multi-port" element (se nedan för detaljer). Varje bindning representerar det momentana flödet av energi ( dE / dt ) eller kraft . Flödet i varje bindning betecknas av ett par variabler som kallas effektvariabler, besläktade med konjugerade variabler , vars produkt är bindningens momentana styrka. Effektvariablerna är uppdelade i två delar: flöde och ansträngning . Till exempel, för bindningen av ett elektriskt system, är flödet strömmen, medan ansträngningen är spänningen. Genom att multiplicera ström och spänning i detta exempel kan du få den momentana effekten av bindningen.

En obligation har två andra egenskaper som beskrivs kortfattat här och diskuteras mer i detalj nedan. Den ena är skyltkonventionen "halvpil". Detta definierar den antagna riktningen för positivt energiflöde. Precis som med elektriska kretsdiagram och frikroppsdiagram är valet av positiv riktning godtyckligt, med förbehållet att analytikern måste vara konsekvent genomgående med den valda definitionen. Den andra egenskapen är "kausaliteten". Detta är en vertikal stång placerad på endast ena änden av bindningen. Det är inte godtyckligt. Som beskrivs nedan finns det regler för att tilldela rätt kausalitet till en given hamn, och regler för företräde bland hamnar. Kausalitet förklarar det matematiska sambandet mellan ansträngning och flöde. Kausaliteternas positioner visar vilka av potensvariablerna som är beroende och vilka som är oberoende.

Om dynamiken i det fysiska systemet som ska modelleras fungerar på vitt varierande tidsskalor, kan snabba kontinuerliga tidsbeteenden modelleras som momentana fenomen genom att använda en hybridbindningsgraf . Obligationsgrafer uppfanns av Henry Paynter .

System för obligationsdiagram

Många system kan uttryckas i termer som används i obligationsdiagram. Dessa termer uttrycks i tabellen nedan.

Konventioner för tabellen nedan:

• $P$ är den aktiva effekten ;
• ${\hat {X}}$ är ett matrisobjekt ;
• ${\vec {x}}$ är ett vektorobjekt ;
• $x^{\dolk }$ är Hermitian av x ; det är det komplexa konjugatet av transponeringen av x . Om x är en skalär, så är Hermitian detsamma som det komplexa konjugatet;
• $D_{t}^{n}$ är Euler-notationen för differentiering, där:
  $$D_{t}^{ n}f(t)={\begin{cases}\displaystyle \int _{-\infty }^{t}f(s)\,ds,&n<0\\[2pt]f(t),&n= 0\\[2pt]{\dfrac {\partial ^{n}f(t)}{\partial t^{n}}},&n>0\end{cases}}$$
• ${\begin{cases}\langle x\rangle ^{\alpha } =|x|^{\alpha }\operatörsnamn {sgn}(x)\\\langle {a}\rangle =k\langle b\rangle ^{\beta}\implies \langle b\rangle =\left({ \frac {1}{k}}\langle a\rangle \right)^{1/\beta }\end{cases}}$
• Vergent-faktor:
  $$\phi _{L}={\begin{cases}{\textrm {Prismatic}}:\ {\dfrac {\textrm {length}}{ {\textrm {tvärsnitt}}\ {\textrm {area}}}}\\{\textrm {Cylinder}}:\ {\dfrac {\ln \left({\frac {\mathrm {radius_{ut} } }{\mathrm {radius_{in}} }}\right)}{2\pi \cdot {\textrm {längd}}}}\\{\textrm {Sfär}}:\ {\dfrac {1}{ 4\pi \left(\mathrm {radius_{in}} \parallel \mathrm {-radius_{out}} \right)}}\end{cases}}$$

	Generaliserat flöde	Generaliserad förskjutning	Generaliserad ansträngning	Generaliserat momentum	Generaliserad effekt (i watt för kraftsystem)	Generaliserad energi (i joule för kraftsystem)
namn	${\vec {f}}(t)$	${\vec {q}}(t)$	${\vec {e}}(t)$	${\vec {p}}(t)$	$P={\vec {f}}(t)^{\dolk }{\vec {e}}(t)$	$E={\vec {q}}(t)^{\dolk }{\vec {e}}(t)$
Beskrivning	Tidsderivata av förskjutning	En egenskap relaterad till statiskt beteende.	Energin per förskjutningsenhet	Tidsintegrering av ansträngning	Omvandling av energi från en till en annan form	Bevarad kvantitet i slutna system
Element
namn	Hyperans $H$ Hyperrigitans $P=H^{-1}$	Överensstämmelse $C$ Rigitans $K=C^{-1}$	Motstånd $R$	Inertans $I$ (eller $L$ )	Abrahance $A$	Magnance $M$
Egenskaper	Kraftförlustelement	Laddningslagringselement (Tillståndsvariabel: förskjutning) (Costate variabel: ansträngning)	Kraftförlustelement	Momentum lagringselement (Tillståndsvariabel: momentum) (Costate variabel: flöde)	Kraftförlustelement	Kraftförlustelement
Kvantitativt beteende	För 1-dimensionella system (linjär): $$P=H\cdot \left(D_{t}^{0}q(t)\right)^{2}$$ För 1-dimensionella system: $$e(t)=P\gamma \left[D_{t}^{-1}q(t)\right]$$ Impedans: $$Z(s)={\frac {1}{s^{2}H}}={\frac {1}{s^{2} }}P$$	Potentiell energi för N-dimensionssystem: $${\begin{array}{lcl}V&=&{\frac {1}{ 2}}{\vec {q}}(t)^{\dolk }{\vec {e}}(t)\\{\vec {q}}(t)&=&{\hat {C}} {\vec {e}}(t)\end{array}}$$ Potentiell energi: $$V=\int _{0}^{q}e(q)\,dq$$ Potentiell samenergi : $${\overline {V}}=\int _{0}^{e}q(e)de$$ För 1-dimensionella system: $$f(t)=C\cdot {\frac {de}{dt}}+e{\frac {dC}{dt}}$$ Impedans: $$Z(s)={\frac {1}{sC}}={\frac {1}{s}}k$$	För 1-dimensionella system (linjär): $$P=R\cdot \left(D_{t}q(t)\right)^{2}$$ Effekt för 1-dimensionella icke-linjära motstånd ( $e(f)$ är ansträngningen som utvecklas av elementet): $$P=e(f)f$$ Rayleigh Power: $${\mathfrak {R}}={\frac {1}{2}}R\cdot f(t)^{2}$$ Rayleigh Power för icke-linjära motstånd: $${\mathfrak {R}}=\int _{0}^{f}e(f)\,df$$ Rayleigh ansträngning: $$e_{\mathfrak {R}}={\frac {d{\mathfrak {R}}}{df}}=e(f)$$ För N-dimensionssystem: $${\begin{array}{lcr}P&=&{\vec {f}}(t )^{\dolk }{\vec {e}}(t)\\{\vec {e}}(t)&=&{\hat {R}}{\vec {f}}(t)\end {array}}$$ För 1-dimensionella system: $$e(t)=R\cdot \gamma \left[D_{t}^{1}q(t)\right]$$ Impedans: $$Z(s)=R$$	Kinetisk energi för N-dimensionssystem: $${\begin{array}{lcl}T={\frac {1}{2 }}{\vec {\rho }}(t)^{\dolk }{\vec {f}}(t)\\{\vec {\rho }}(t)={\hat {L}}{ \vec {f}}(t)\end{array}}$$ Rörelseenergi: $$T=\int _{0}^{\rho }f(\rho )\,d\rho$$ Kinetisk samenergi: $${\overline {T}}=\int _{0}^{f}\rho (f)\,df$$ För 1-dimensionella system: $$e(t)=L\cdot {\frac {df}{dt}}+f\cdot {\frac {dL}{ dt}}$$ Impedans: $$Z(s)=sL$$	För 1-dimensionella system (linjär): $$P=A\cdot \left(D_{t}^{2}q(t)\right)^{2}$$ För 1-dimensionella system: $$e(t)=A\cdot \gamma \left[D_{t}^{3}q(t)\right]$$ Impedans $$Z(s)=s^{2}A$$	För 1-dimensionella system (linjär) $$P=A\cdot \left(D_{t}^{3}q(t)\right)^{2}$$ För 1-dimensionella system $$e(t)=M\cdot \gamma \left[D_{t}^{5}q(t)\right]$$ Impedans $$Z(s)=s^{4}M$$
Generaliserat beteende	Energi från aktiva ansträngningskällor: $W=\int _{0}^{q}{e_{\text{källa}}}\,dq$ Lagrangian : ${\mathfrak {L}}=T-(VW)$ Hamiltonian : ${\mathfrak {H}}=T+(VW)$ Hamiltonsk ansträngning: $e_{\mathfrak {H}}={\frac {d{\mathfrak {H}}}{dq}}$ Lagrangansträngning: $e_{\mathfrak {L}}={\frac {d{\mathfrak {L}}}{dq}}$ Passiv ansträngning: $e_{\mathfrak {LH}}={\frac {d}{dt}}{\frac {d{\mathfrak {L}}}{ df}}$ Effektekvation: ${\frac {d{\mathfrak {L}}}{dt}}+{\frac {d{\mathfrak {H}}}{dt} }=0$ Ansträngningsekvation: $e_{\mathfrak {L}}+e_{\mathfrak {H}}=0$ Lagrangekvation: $e_{\mathfrak {R}}+e_{\mathfrak {LH}}=e_{\mathfrak {L}}$ Hamiltonsk ekvation: $e_{\mathfrak {R}}+e_{\mathfrak {LH}}=-e_{\mathfrak {H}}$ Om ${\overline {W}}$ är samenergin, $W$ är energin, $S$ är tillståndsvariabeln och ${\overline {S} }$ är costate-variabeln, ${\begin{aligned}{\overline {W}} +W=S\cdot {\overline {S}}\\{\overline {W}}=\int _{0}^{\overline {S}}S({\overline {S}})\,d {\overline {S}}\\W=\int _{0}^{S}{\overline {S}}(S)dS\end{aligned}}$ För linjära element: ${\overline {W}}=W={\frac {1}{2}}S\cdot {\overline {S}}$

Längsgående mekaniskt kraftsystem

Flödesrelaterade variabler	$D_{t}^{6}x$ : Pounce / Pop $\mathrm {[m/s^{6}]}$	$D_{t}^{5}x$ : Volang / Crackle $\mathrm {[m/s^{5}]}$	$D_{t}^{4}x$ : Jounce / Snap $\mathrm {[m/s^{4}]}$	$D_{t}^{3}x$ : Ryck $\mathrm {[m/s^{3}]}$
	$D_{t}^{2}x$ : Acceleration $(x_{2t})\ \mathrm {[m/s^{2 }]}$	$D_{t}^{1}x$ : Hastighet $(x_{t})\ \mathrm {[m/s]}$ (Flöde )	$D_{t}^{0}x$ : Förskjutning $(x)\ \mathrm {[m]}$ (förskjutning)	$D_{t}^{-1}x$ : Absement $\mathrm {[m\cdot s]}$
	$D_{t}^{-2}x$ : Absitet $\mathrm {[m\cdot s^{2}]}$	$D_{t}^{-3}x$ : Abseleration $\mathrm {[m\cdot s^{3}]}$	$D_{t}^{-4}x$ : Abserk $\mathrm {[m\cdot s^{4}]}$
Ansträngningsrelaterade variabler	$D_{t}^{1}F$ : Yank $\mathrm {[N/s]}$	$D_{t}^{0}F$ : Force $(P_{x}^{t})\ \mathrm {[N]}$ (Ansträngning )	$D_{t}^{-1}F$ : Linjärt momentum $(P_{x}^{2t})\ \mathrm {[kg\cdot m/s]}$ (Momentum)
Passiva element
Efterlevnad (C)	Motstånd (R)	Tröghet (I)	Abrahance (A)	Magnance (M)
Vår $$\langle P_{x}^{t}\rangle =k\langle x\rangle$$ där $k$ är fjäderstyvheten	Spjäll $$\langle P_{x}^{t}\rangle =b\langle x_{t}\rangle$$ där $b$ är spjällparametern	Massa $$\langle P_{x}^{t}\rangle =m\langle x_{2t}\rangle$$ där $m$ är massan	Abraham–Lorentz styrka $$\langle P_{x}^{t}\rangle ={\frac {\mu _{0}q^{2}}{ 6\pi c}}\langle x_{3t}\rangle$$ var $\mu _{0}$ är permeabiliteten $q$ är den elektriska laddningen $c$ är ljusets hastighet	Magnetisk strålningsreaktionskraft $$​​{\displaystyle \langle P_{q}^{t}\rangle ={\frac {\mu _{0}q^{2} R}{24\pi c^{3}}}\langle x_{5t}\rangle }$$ var $\mu _{0}$ är permeabiliteten $q$ är den elektriska laddningen $c$ är ljusets hastighet $R$ är radien för det magnetiska momentet
Konsol $$\langle P_{x}^{t}\rangle ={\frac {3EI}{L^{3}}}\langle x\rangle$$ $L$ : Fribärande längd $E$ : Youngs modul $I$ : Andra momentet av området	Cyklotronstrålningsmotstånd $$\langle P_{x}^{t}\rangle ={\frac {\sigma _{t}B^{2}}{c \mu _{0}}}\langle x_{t}\rangle$$ var $\sigma _{t}$ : Thompson-tvärsnitt $c$ : Ljushastighet $\mu _{0}$ : Permeabilitet $B$ : Magnetisk fälttäthet
Prismatisk flytare i en bred vattenkropp $$\langle P_{x}^{t}\rangle =\rho _{L}gA\langle x\rangle$$ var $\rho _{L}$ : Vätskedensitet $A$ : Area $g$ : Gravitationsacceleration	Viskös friktion $$\langle P_{x}^{t}\rangle =b\langle x_{t}\rangle$$ där $b$ är den viskösa friktionsparametern
Elastisk stång $$\langle P_{x}^{t}\rangle ={\frac {EA}{L}}\langle x\rangle$$ var $E$ : Youngs modul $A$ : Area $L$ : Spölängd	Invers av kinetisk rörlighet $$\langle P_{x}^{t}\rangle ={\frac {1}{\mu }}\langle x_{t}\rangle$$ där $\mu$ är den kinetiska rörligheten
Newtons gravitationslag $$\langle P_{x}^{t}\rangle =GMm\langle x\rangle ^{-2}$$ var $G$ : Gravitationskonstant $M$ : Kroppsmassa 1 $m$ : Kroppsmassa 2	Geometri som interagerar med luft (t.ex. drag ) $$\langle P_{x}^{t}\rangle ={\frac {1}{2}}c\rho A\langle x_{ t}\rangle ^{2}$$ var $A$ : Kontaktyta $c$ : Aerodynamisk geometrikoefficient $\rho$ : Vätskedensitet
Coulombs lag $$\langle P_{x}^{t}\rangle ={\frac {Qq}{4\pi \varepsilon _{0}}} \langle x\rangle ^{-2}$$ var $\varepsilon _{0}$ : Permittivitet $Q$ : Laddning av kroppen 1 $q$ : Laddning av kroppen 2	Absquare dämpare $$\langle P_{x}^{t}\rangle =B\langle x_{t}\rangle ^{2}$$ där $B$ är parametern Absquare spjäll
Casimir styrka $$\langle P_{x}^{t}\rangle ={\frac {A\hbar c\pi ^{2}}{240 }}\langle x\rangle ^{-4}$$ var $A$ : Plattans area $\hbar$ : Plancks reducerade konstant $c$ : Ljushastighet	Torr friktion $$\langle P_{x}^{t}\rangle =\mu F_{n}\langle x_{t}\rangle ^{0}$$ var $\mu$ : Kinetisk friktionskoefficient $F_{n}$ : Normal kraft
Biot-Savart lag $$\langle P_{x}^{t}\rangle ={\frac {\mu _{0}I_{1}I_ {2}l}{2\pi }}\langle x\rangle ^{-1}$$ var $\mu _{0}$ : Permeabilitet $I_{1}$ : Ström i tråd 1 $I_{2}$ : Ström i tråd 2 $l$ : Längd på trådar
Kolvpressande vätska inuti en adiabatisk kammare $$P_{x}^{t}=AP_{0}\left(1+{\frac {x}{x_{0}}}\right )^{-\gamma }$$ var $A$ : Arean av kolven $P_{0}$ : Initialt tryck inuti $x_{0}$ : Initial position för kolven $\gamma$ : Poissonkoefficient

Vinkelt mekaniskt kraftsystem

Flödesrelaterade variabler	$D_{t}^{3}\theta$ : Vinkelryck $\mathrm {[rad/s^{3}]}$	$D_{t}^{2}\theta$ : Vinkelacceleration $(\theta _{2t})\ \mathrm {[ rad/s^{2}]}$
	$D_{t}^{1}\theta$ : Vinkelhastighet $(\theta _{t})\ \mathrm {[rad/ s]}$ (Flöde)	$D_{t}^{0}\theta$ : Vinkelförskjutning $(\theta )\ \mathrm {[rad]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{1}\tau$ : Rotatum $\mathrm {[W/rad]}$	$D_{t}^{0}\tau$ : Moment $(P_{\theta }^{t})\ \mathrm {[ J/rad]}$ (Ansträngning)
	$D_{t}^{-1}\tau$ : Vinkelmoment $(P_{\theta }^{2t })\ \mathrm {[J\cdot s/rad]}$ (Momentum)
Passiva element
Efterlevnad (C)	Motstånd (R)	Tröghet (I)
Invers av vinkelfjäderkonstanten $$\langle P_{\theta }^{t}\rangle =k_{r}\langle \theta \rangle$$ där $k_{r}$ är vinkelfjäderkonstanten	Vinkeldämpning $$\langle P_{\theta }^{t}\rangle =R\langle \theta _{t}\rangle$$ där $R$ är dämpningskonstanten	Masströghetsmoment Skriv $\langle P_{\theta }^{t}\rangle =I\langle \theta _{2t}\rangle$ där $I$ är masströghetsmomentet
Rod Torsion $$\langle P_{\theta }^{t}\rangle ={\frac {GJ}{L}}\langle \theta \rangle$$ var $G$ : Skjuvmodul $J$ : Polärt moment för arean $L$ : Spölängd	Guvernör (t.ex. används i speldosor) $$\langle P_{\theta }^{t}\rangle =R\langle \theta _{t}\rangle ^{2}$$ där $R$ är regulatorkonstanten
Böjmoment (cantilever) $$\langle P_{\theta }^{t}\rangle ={\frac {EI}{L}}\langle \theta \rangle$$ var $E$ : Ung modul $I$ : Andra momentet av området $L$ : Strållängd
Parallellt kraftfält $$\langle P_{\theta }^{t}\rangle =\langle P_{x}^{t}\rangle \sin \ vänster(\alpha -\theta \right)$$ var $\alpha$ : Vinkel (moturs positiv) mellan polaxeln och kraftfältet $\theta$ : Aktuell vinkel för objektet (t.ex. pendel)

Elkraftsystem

Flödesrelaterade variabler	$D_{t}^{2}q$ : Elektrisk tröghet $\mathrm {[A/s]}$	$D_{t}^{1}q$ : Elektrisk ström $(q_{t})\ \mathrm {[A]}$ (Flöde)	$D_{t}^{0}q$ : Elektrisk laddning $(q)\ \mathrm {[C]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{1}V$ : Distension $\mathrm {[V/s]}$	$D_{t}^{0}V$ : Spänning $(P_{q}^{t})\ \mathrm {[V]}$ (Ansträngning )	$D_{t}^{-1}V$ : Fluxlänkage ${\displaystyle (P_{q }^{2t})\ \ \mathrm {[V\cdot s]} {\text{ eller }}\mathrm {[Wb\cdot turn]} } (Momentum$ )
Element
Hyperans (H)	Efterlevnad (C)	Motstånd (R)	Tröghet (I)	Abrahance (A)
Frekvensberoende negativt motstånd (FDNR) $$\langle P_{q}^{t}\rangle ={\frac {1}{H}}\langle q^{t}\rangle$$	Linjär kondensator $$\langle P_{q}^{t}\rangle ={\frac {1}{\varepsilon }}\phi _{L}\langle q\ rangle$$ var $\varepsilon$ : Permittivitet $\phi _{L}$ : Vergent-faktor	Linjärt motstånd $$\langle P_{q}^{t}\rangle =\rho \phi _{L}(1+ \alpha (T-T_{0}))\langle q_{t}\rangle$$ var $\rho$ : Resistivitet $\phi _{L}$ : Vergent-faktor $\alpha$ : Termisk koefficient $T$ : Aktuell temperatur $T_{0}$ : Referenstemperatur	Linjär induktor (solenoid) $$\langle P_{q}^{t}\rangle ={\frac {\mu _{0}N^{2}A}{ L}}\langle q_{2t}\rangle$$ var $\mu _{0}$ : Permeabilitet $N$ : Antal varv $A$ : Area $L$ : Längd	Frekvensberoende negativ konduktans (FDNC) Typ $$\gamma ^{1}\iff V=RD_{t}^{2}i\quad [H\cdot s]$$
		Diod $$P_{q}^{t}=nV_{T}\ln \left(1+{\frac {q_{t}}{ Är rätt)$$ var $n$ : Idealitetsfaktor $V_{T}$ : Termisk spänning $I_{s}$ : Läckström	Toroid $$\langle P_{q}^{t}\rangle ={\frac {\mu N^{2}A}{2\ pi r}}\langle q_{2t}\rangle$$ var $\mu$ : Permeabilitet $N$ : Antal varv $A$ : Tvärsnittsarea $r$ : Toroidradie till mittlinje
Intra-Gyrator			Inter-Gyrator
Kompatibel Gyrator	Resistiv Gyrator	Inertant Gyrator
	Halleffektanordning $${\begin{aligned}e_{x}=R_{H}{\frac {B_{z}}{ t_{z}}}i_{y}\\e_{y}=R_{H}{\frac {B_{z}}{t_{z}}}i_{x}\end{aligned}}$$ var $R_{H}$ : Hallkoefficient $B_{z}$ : Vertikalt magnetiskt induktionsfält $t_{z}$ : Vertikal tjocklek	Induktionsmotor $${\begin{aligned}e_{r}^{1}=M\cos(\theta )D_{t}f_{s}^{1}+f_{s} ^{1}D_{t}\left[M\cos(\theta )\right]\\e_{s}^{1}=M\cos(\theta )D_{t}f_{r}^{1 }+f_{r}^{1}D_{t}\left[M\cos(\theta )\right]\end{aligned}}$$ var $\theta$ : Elektrisk vinkel $e_{r}^{1}$ : Spänning vid rotorstången $e_{s}^{1}$ : Spänning vid statorstången $f_{s}^{1}$ : Flöde genom statorstången $f_{r}^{1}$ : Flöde genom rotorstången	likströmsmotor $${\begin{aligned}\tau _{e}=k_{a}\phi _ {a}(i_{e})i_{a}\\\omega _{e}={\frac {1}{k_{a}\phi _{a}(i_{e})}}e_{a }\end{aligned}}$$ var $\tau _{e}$ : Elektromagnetiskt vridmoment $\omega _{e}$ : Axelns vinkelhastighet $i_{e}$ : Fältström $i_{a}$ : Armaturström	Faraday gyrator $${\begin{aligned}F&=Bli\\V&={\frac {1}{Bl}}v\end{aligned}}$$ var $F$ : Force $v$ : Stånghastighet $V$ : Stångspänning $B$ : Magnetiskt induktionsfält $l$ : Spölängd
			Faraday disk $${\begin{aligned}V&={\frac {1}{2}}Br^{2}\omega \\\tau &= {\frac {1}{2}}Br^{2}i\end{aligned}}$$ var $B$ : Magnetiskt induktionsfält $r$ : Diskradie
Intratransformator			Inter-transformator
Elektrisk transformator ( endast för AC-signaler ) $${\begin{aligned}V_{2}&={\frac {N_{2}}{N_{1}}}V_ {1}\\f_{2}&={\frac {N_{1}}{N_{2}}}f_{1}\end{aligned}}$$

Hydrauliskt / pneumatiskt kraftsystem

Flödesrelaterade variabler	$D_{t}^{1}V$ : Volumetrisk flödeshastighet $(V_{t})\ \mathrm {[m^{3} /s]}$ (Flöde)	$D_{t}^{0}V$ : Volym $(V)\ \mathrm {[m^{3}]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}P$ : Tryck $​​{\displaystyle (P_{V}^{t})\ \mathrm {[Pa]} }$ ( Ansträngning)	$D_{t}^{-1}P$ : Vätskemomentum $(P_{V}^{2t})\ \mathrm {[Pa\cdot s]}$ (Momentum)
Element
Efterlevnad (C)	Motstånd (R)	Tröghet (I)
Rörelasticitet $$\langle P_{V}^{t}\rangle =\left({\frac {t_{W}E}{2r_{0 }V_{0}}}\right)\langle V\rangle$$ var $r_{0}$ : Nominell rörradie $V_{0}$ : Rörvolym (utan stress) $t_{W}$ : Väggtjocklek $E$ : Youngs modul	Darcy svamp $$\langle P_{V}^{t}\rangle =\left({\frac {\mu }{k}}\phi _{ L}\right)\langle V_{t}\rangle$$ var $\mu$ : Dynamisk viskositet $k$ : Permeabilitet $\phi _{L}$ : Vergent-faktor	Vätsketröghet i rör $$\langle P_{V}^{t}\rangle =\left(\rho \phi _{L}\right)\langle V_{ 2t}\rangle$$ var $\rho$ : Vätskedensitet $\phi _{L}$ : Vergent-faktor
Kompressibel vätska (ungefär) $$\langle P_{V}^{t}\rangle =\left({\frac {B }{V_{0}}}\right)\langle V\rangle =\underbrace {\left({\frac {\rho _{0}c^{2}}{V_{0}}}\right)} _{\begin{array}{c}{\text{Acoustic}}\\{\text{Upprängning}}\end{array}}\langle V\rangle$$ var $V_{0}$ : Rörvolym (utan stress) $B$ : Bulkmodul $\rho _{0}$ : Gasdensitet vid referenstryck $c$ : Ljudhastighet	Ventil $$\langle P_{V}^{t}\rangle =\left({\frac {\rho }{2C_{d }^{2}A_{0}^{2}}}\right)\langle V_{t}\rangle ^{2}$$ $C_{d}$ : Urladdningskoefficient $\rho$ : Vätskedensitet $A_{0}$ : Minsta område för vätskepassage
Tank med area ${\textstyle A{\frac {1}{[m]^{n-1}}}\left(h+h_{0} \right)^{n-1}}$ : $$P_{V}^{t}=\rho gh_{0}\left [\left(1+{\frac {nV}{A{\frac {1}{[m]^{n-1}}}h_{0}^{n}}}\höger)^{1/n }-1\höger]$$ var $h$ : Höjd i förhållande till marken $h_{0}$ : Inloppshöjd $\rho$ : Vätskedensitet $A$ : Kurvskalning (ytas dimension) $[m]^{n-1}$ : Korrigering av dimension $n$ : Kurvparameter $g$ : Tyngdacceleration Fall $n=1$ (prismatiskt fall): $$P_{V}^{t}={\frac {\rho g}{A}}V$$ Fall $n=0$ (aktuellt diodhus): $$P_{V}^{t}=\rho gh_{0}\left(e^{\frac {V}{A[m ]}}-1\höger)$$	Poiseuille motstånd för cylindrar $$\langle P_{V}^{t}\rangle =\left({\frac {8\mu L}{\pi R ^{4}}}\right)\langle V_{t}\rangle$$ var $\mu$ : Dynamisk viskositet $L$ : Rörlängd $R$ : Rörradie
Isotermisk kammare $$\langle P_{V}^{t}\rangle =k\langle V_{t}\rangle ^{-1}$$ där $k$ är kammarens konstant	Turbulensmotstånd $$\langle P_{V}^{t}\rangle =a_{t}\langle V_{t}\rangle ^{\frac {7}{ 4}}$$ där $a_{t}$ är en empirisk parameter
Kompressibel vätska $$P_{V}^{t}=-B\ln V$$ där $B$ är bulkmodulen	Munstycke $$\langle P_{V}^{t}\rangle ={\frac {\rho }{2\vänster (A_{\text{out}}^{2}\parallel -A_{\text{in}}^{2}\right)}}\langle V_{t}\rangle ^{2}$$ var $\rho$ : Vätskedensitet $A_{\text{out}}$ : Utloppsområde $A_{\text{i}}$ : Inloppsområde
Adiabatisk blåsa $$P_{V}^{t}=P_{V,0}^{t}\left(1-{\frac {V}{ V_{0}}}\höger)^{-\gamma }$$ var $P_{V,0}^{t}$ : Referenstryck $V_{0}$ : Referensvolym $\gamma$ : Poissonkoefficient	Backventil $$P_{V}^{t}=k\ln \left(1+{\frac {V_{t}}{V_{t, 0}}}\right)$$ var $k$ : Empirisk konstant $V_{t,0}$ : Omvänd bias absolut flöde

Gyrator-kondensator kraftsystem

Flödesrelaterade variabler	$D_{t}^{0}\varphi$ : Magnetiskt flöde $(\varphi )\ \mathrm {[Wb]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}{\mathcal {F}}$ : Magnetomotorisk kraft $({\mathcal {F}})\ \ \ mathrm {[A\cdot turn]}$ (Momentum)
Element
Efterlevnad (C)	Motstånd (R)	Tröghet (I)
Permeans ( ${\mathcal {P}}$ ) $$\langle {\mathcal {F}}\rangle ={\frac {1}{\mu }}\phi _{ L}\langle \varphi \rangle \quad \mathrm {[H/sväng^{2}]}$$ var $\mu$ : Permeabilitet $\phi _{L}$ : Vergent-faktor	Magnetisk komplex impedans ( $Z_{M}$ ) $${\mathcal {F}}=Z_{M}{\varphi _{t}}\quad \mathrm {[{turn}^{2 }/\Omega ]}$$	Magnetisk komplex induktans ( $L_{M$ ) $${\mathcal {F}}=L_{M}{\varphi _{2t}}\quad \mathrm {[{turn}^{2 }F]}$$

Gravitationskraftsystem

Flödesrelaterade variabler	$D_{t}^{0}i_{g}$ : Gravitationsströmslinga ${\displaystyle \left(i_{g }=2\varepsilon _{g}v_{\text{orbit}}^{3}\right)\ \mathrm {[kg/s]} } ($ Flöde)	$D_{t}^{-1}i_{g}$ : Gravitationsladdning $(M)\ \mathrm {[kg]}$ (förskjutning )
Ansträngningsrelaterade variabler	$D_{t}^{0}V_{g}$ : Gravitationsspänning $\left(V_{ g}={\frac {1}{2}}{\frac {v_{\text{orbit}}^{4}}{c^{2}}}\right)\ \mathrm {[m^{2 }/s^{2}]}$ (Ansträngning)	$D_{t}^{-1}V_{g}$ : Gravitationsmomentum $\left( \phi _{g}={\frac {\pi v_{\text{orbit}}^{3}r}{c^{2}}}\right)\ \mathrm {[m^{2}/s ]}$ (Momentum)
Element
Efterlevnad (C)	Motstånd (R)	Tröghet (I)
Gravitationskapacitans Typ $\gamma ^{1}\iff M_{g}=CV_{g}\quad \mathrm {[kg/m^{2} ]}$ $C_{g}={\frac {2c^{2}r^{2}}{GM}}$	Gravitationellt omloppsmotstånd Typ $\gamma ^{1}\iff V_{g}=R_{g}i_{g}\quad \mathrm {[ m^{2}/kg\cdot s]}$ $R_{g}={\frac {\mu _{g}}{4}}v_{\text{omlopp}}$	Gravitationsinduktans Skriv $\gamma ^{1}\iff \phi _{g}=Ii_{g}\quad \mathrm {[m^ {2}/kg\cdot s^{2}]}$ $L_{g}={\frac {2\pi ^{2}G}{c^{2}}}r$

Elektriskt fältvolymetrisk effekttäthetssystem

Flödesrelaterade variabler	$D_{t}^{0}J$ : Strömdensitet $(J)\ \mathrm {[A/m^{2}]}$ ( Flöde)	$D_{t}^{-1}J$ : Elektriskt förskjutningsfält $(D)\ \mathrm {[C/m^{2} ]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}E$ : Elektriskt fält $(E)\ \mathrm {[V/m]}$ (Ansträngning)	$D_{t}^{-1}E$ : Magnetisk potentialvektor $(A)\ \mathrm {[V\cdot s/m ]}$ (Momentum)
Element
Efterlevnad (C)	Motstånd (R)	Volumetrisk effekttäthetsinertans ( $I_{V$ )
Elektrisk tillåtelse Typ $\gamma ^{1}\iff D=\epsilon _{0}E\quad \mathrm {[F/m]}$	Elektrisk resistans Typ $\gamma ^{1}\iff E=\rho J\quad \mathrm {[\Omega m]}$	Magnetisk permeabilitet $\mu _{0}\ \mathrm {[H/m]}$

Magnetfälts volymetrisk effekttäthetssystem

Flödesrelaterade variabler	$D_{t}^{0}B$ : Magnetisk flödestäthet $(B)\ \mathrm {[T]} {\ text{ eller }}\mathrm {[Wb/m^{2}]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}H$ : Magnetisk fältstyrka $(H)\ \mathrm {[A\cdot {turn} /m]}$ (Ansträngning)
Element
Efterlevnad (C)	Motstånd (R)	Volumetrisk effekttäthetsinertans ( $I_{V$ )
Magnetisk permeabilitet för magnetiska kretsar Typ $\gamma ^{1}\iff B=\mu H\quad \mathrm {[H/(m\cdot { sväng}^{2})]}$

Gravitoelektriskt volymetrisk effekttäthetssystem

Flödesrelaterade variabler	$D_{t}^{0}J_{g}$ : Massflöde $(J_{g})\ \mathrm {[ kg/m^{2}s]}$ (flöde)	$D_{t}^{-1}J_{g}$ : Ackumulerat massaflöde ${\displaystyle (D_{g})\$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}g$ : Gravityacceleration $(g)\ \mathrm {[m/s^{2}]}$ (Ansträngning)
Element
Efterlevnad (C)	Motstånd (R)	Volumetrisk effekttäthetsinertans ( $I_{V$ )
Gravitationstillstånd Typ $\gamma ^{1}\iff D_{g}=\epsilon _{g}g\quad \mathrm {[kg \cdot s^{2}/m^{3}]}$ $\varepsilon _{g}={\frac {1}{4\pi G}}$		Gravitationspermeabilitet $\mathrm {[m/kg]}$ $$I_{V}=\mu _{g}={\frac {4\pi G}{c^{2}}}$$

Gravitomagnetiskt volymetrisk effekttäthetssystem

Flödesrelaterade variabler	$D_{t}^{0}B_{g}$ : Gravitomagnetiskt fält $\left(B_{g} =\omega _{\text{orbit}}\left({\frac {v_{\text{orbit}}}{c}}\right)^{2}\right)\ \mathrm {[Hz]}$ (Förflyttning)
Ansträngningsrelaterade variabler	$D_{t}^{0}H_{g}$ : Gravitomagnetisk fältstyrka $(H_{g})\ \mathrm {[Pa\ cdot s]}$ (Ansträngning)
Element
Efterlevnad (C)	Motstånd (R)	Volumetrisk effekttäthetsinertans ( $I_{V$ )
Gravitationspermeabilitet $-{\frac {4\pi G}{c^{2}}}\ \mathrm {[m/kg]}$

Termiskt effekt-temperatursystem

Flödesrelaterade variabler	$D_{t}^{1}Q$ : Värmehastighet $(\psi _{t})\ \mathrm {[W]}$ (Flöde )	$D_{t}^{0}Q$ : Total värme $(\psi )\ \mathrm {[J]}$ (förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}T$ : Temperatur $(T)\ \mathrm {[K]}$ (Ansträngning)
Element
Efterlevnad (C)	Motstånd (R)	Tröghet (I)
Isobarisk värme $$T={\frac {1}{\rho Vc_{p}}}\psi ={\frac {1}{C_{P}}}\ psi$$ var $\rho$ : Objektets massdensitet $V$ : Volym av objekt $c_{p}$ : Tryckspecifik värmekapacitet	Ledningsmotstånd $$T={\frac {1}{k}}\phi _{L}\psi _{t}$$ var $k$ : Värmeledningsförmåga $\phi _{L}$ : Vergent-faktor
Isokorisk värme $$T={\frac {1}{C_{V}}}\psi$$ där $C_{V}$ är värmekapacitansen med konstant volym	Konvektionsmotstånd $$T={\frac {1}{hA}}\psi _{t}$$ var $h$ : Konvektionskoefficient $A$ : Gränssnittsområde
Isotermisk värme $$T={\frac {1}{nR\ln \left({\frac {V_{f}}{V_{i}}}\right )}}\psi$$ var $R$ : Universell gaskonstant $n$ : Antal mol $V_{f}$ : Slutvolym $V_{i}$ : Initial volym	Stefan-Boltzmann lag $$\langle T\rangle =\left({\frac {1}{e\sigma A}}\right)^{0,25}\langle \psi _{t}\rangle ^{0.25}$$ var $e$ : Emissivitet $\sigma$ : Stefan-Boltzmann konstant $A$ : Gränssnittsområde

Kontinuummekanik volymetriskt effekttäthetssystem

Flödesrelaterade variabler	$D_{t}^{1}\varepsilon$ : Töjningshastighet $({\dot {\varepsilon }})\ \mathrm {[Hz] }$ (Flöde)	$D_{t}^{0}\varepsilon$ : Töjning $(\varepsilon )\ \mathrm {[1]}$ (Förskjutning)
Ansträngningsrelaterade variabler	$D_{t}^{0}\sigma$ : Stress $​​{\displaystyle (\sigma )\ \mathrm {[Pa]} }$ (Ansträngning)
Element
Efterlevnad (C)	Motstånd (R)	Volumetrisk effekttäthetsinertans ( $I_{V$ )
Invers av stelhet Typ $\gamma ^{1}\iff \varepsilon =C\sigma \quad \mathrm {[Pa^{-1}]$ $C={\frac {1}{K}}$	Viskositet Typ $\gamma ^{1}\iff \sigma =R{\dot {\varepsilon }}\quad \mathrm {[Pa\cdot s]}$	Power Density Inertance: Materialdensitet $\rho \ \mathrm {[kg/m^{3}]}$

Andra system:

• Termodynamiskt kraftsystem (flödet är entropihastighet och ansträngning är temperatur)
• Elektrokemiskt kraftsystem (flöde är kemisk aktivitet och ansträngning är kemisk potential)
• Termokemiskt kraftsystem (flödet är masshastighet och ansträngning är massspecifik entalpi)
• Makroekonomins valutakurssystem (förskjutning är en vara och ansträngning är pris per vara)
• Mikroekonomins valutakurssystem (förflyttning är befolkning och ansträngning är BNP per capita)

Statens tetraeder

Statens tetraeder

Statens tetraeder är en tetraeder som grafiskt visar omvandlingen mellan ansträngning och flöde. Den intilliggande bilden visar tetraedern i dess generaliserade form. Tetraedern kan modifieras beroende på energidomänen.

Med hjälp av statens tetraeder kan man hitta ett matematiskt samband mellan alla variabler på tetraedern. Detta görs genom att följa pilarna runt diagrammet och multiplicera eventuella konstanter längs vägen. Till exempel, om du ville hitta sambandet mellan generaliserat flöde och generaliserat förskjutning, skulle du börja vid f ( t ) och sedan integrera det för att få q ( t ) . Fler exempel på ekvationer kan ses nedan.

Samband mellan generaliserad förskjutning och generaliserat flöde.

$$q(t)=\int f(t)\,dt$$

Samband mellan generaliserat flöde och generaliserat ansträngning.

$$f(t)={\frac {1}{R}}\cdot e(t)$$

Samband mellan generaliserat flöde och generaliserat momentum.

$$f(t)={\frac {1}{I}}\cdot p(t)$$

Samband mellan generaliserat momentum och generaliserat ansträngning.

$$p(t)=\int e(t)\,dt$$

Förhållandet mellan generaliserat flöde och generaliserat ansträngning, som involverar konstanten C.

$$e(t)={\frac {1}{C}}\int f(t)\,dt$$

Alla matematiska samband förblir desamma när man byter energidomäner, bara symbolerna ändras. Detta kan ses med följande exempel.

Samband mellan förskjutning och hastighet.

$$x(t)=\int v(t)\,dt$$

Förhållandet mellan ström och spänning, detta är också känt som Ohms lag .

$$i(t)={\frac {1}{R}}V(t)$$

Förhållandet mellan kraft och förskjutning, även känd som Hookes lag . Det negativa tecknet tas bort i denna ekvation eftersom tecknet är inkluderat i hur pilen pekar i bindningsgrafen.

$$F(t)=kx(t)$$

För kraftsystem är formeln för resonansfrekvensen följande:

$$\omega ={\sqrt {\frac {1}{LC}}}$$

För effekttäthetssystem är formeln för hastigheten för resonansvågen följande:

$$c={\sqrt {\frac {1}{LC}}}$$

Komponenter

Om en motor är ansluten till ett hjul genom en axel, överförs kraften i den rotationsmekaniska domänen, vilket innebär att ansträngningen och flödet är vridmoment (τ) respektive vinkelhastighet (ω). En ordbindningsgraf är ett första steg mot en bindningsgraf, där ord definierar komponenterna. Som ett ordbindningsdiagram skulle detta system se ut så här:

$${\text{motor}}\;{\overset {\textstyle \tau }{\underset {\textstyle \omega }{-\!\!\!-\! \!\!-\!\!\!-\!\!\!-}}}\;{\text{hjul}}$$

En halvpil används för att ge en teckenkonvention, så om motorn utför arbete när τ och ω är positiva, så skulle diagrammet ritas:

$${\text{motor}}\;{\overset {\textstyle \tau }{\underset {\textstyle \omega }{-\!\!\!-\!\ !\!-\!\!\!\rightharpoondown }}}\;{\text{hjul}}$$

Detta system kan också representeras i en mer generell metod. Detta innebär att man byter från att använda orden till symboler som representerar samma föremål. Dessa symboler är baserade på den generaliserade formen, som förklarats ovan. Eftersom motorn applicerar ett vridmoment på hjulet, kommer det att representeras som en källa till ansträngning för systemet. Hjulet kan presenteras av en impedans på systemet. Vidare tappas symbolerna för vridmoment och vinkelhastighet och ersätts med de generaliserade symbolerna för ansträngning och flöde. Även om det inte är nödvändigt i exemplet, är det vanligt att numrera obligationerna för att hålla reda på i ekvationer. Det förenklade diagrammet kan ses nedan.

$${S_{e}}\;{\overset {\textstyle e_{1}}{\underset {\textstyle f_{1}}{-\!\! \!-\!\!\!-\!\!\!\rightharpoondown }}}\;{\text{I}}$$

Med tanke på att ansträngningen alltid ligger över flödet på obligationen, är det också möjligt att släppa ansträngnings- och flödessymbolerna helt utan att förlora någon relevant information. Obligationsnumret bör dock inte tas bort. Exemplet kan ses nedan.

$${S_{e}}\;{\overset {\textstyle _{1}}{\underset {\textstyle }{-\!\!\!-\!\! \!-\!\!\!\rightharpoondown }}}\;{\text{I}}$$

Obligationsnumret kommer att vara viktigt senare när man konverterar från obligationsgrafen till state-space-ekvationer.

Sammanslutning av element

Serieförening

Antag att ett element har följande beteende:

$$e(t)=\alpha g(q(t))$$

där $g(x)$ är en generisk funktion (den kan till och med differentiera/integrera dess input) och $\alpha$ är elementets konstant. Anta sedan att du i en 1-korsning har många av den här typen av element. Då är den totala spänningen över korsningen:

$$e(t)=\left(\summa _{i}\alpha _{ i}\right)g(q(t))\implicerar {\begin{array}{||c||}\hline \displaystyle \alpha _{\text{eq}}=\summa _{i=1} ^{N}\alpha _{i}\\\hline \end{array}}$$

Parallell förening

Antag att ett element har följande beteende:

$$e(t)=g(\alpha q(t))$$

där $g(x)$ är en generisk funktion (den kan till och med differentiera/integrera dess input) och $\alpha$ är elementets konstant. Anta sedan att du i en 0-korsning har många av den här typen av element. Då är det giltigt:

$$g ^{-1}\left(e(t)\right)=\alpha _{i}q_{i}(t)\implicerar {\frac {1}{\alpha _{i}}}g^{- 1}(e(t))=q_{i}(t)\implies \left(\summa _{i}{\frac {1}{\alpha _{i}}}\right)g^{-1 }(e(t))=q(t)\implicerar g(g^{-1}(e(t)))=g\left({\frac {1}{\sum _{i}{\frac {1}{\alpha _{i}}}}}q(t)\right)\implicerar {\begin{array}{|c|}\hline \alpha _{\text{eq}}=\parallel _ {i=1}^{N}\alpha _{i}\\\hline \end{array}}$$

Enkelportselement

Enkelportselement är element i en bindningsgraf som bara kan ha en port.

Källor och sänkor

Källor är element som representerar indata för ett system. De kommer antingen lägga in ansträngning eller flöda in i ett system. De betecknas med stort "S" med antingen gemener "e" eller "f" för ansträngning respektive flöde. Källor kommer alltid att ha pilen som pekar bort från elementet. Exempel på källor inkluderar: motorer (källa till ansträngning, vridmoment), spänningskällor (källa till ansträngning) och strömkällor (källa till flöde).

$$S_{e}\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\ !\!-\!\!\!\rightharpoonup \!\!\!}}}\;\ J\qquad {\text{and}}\qquad S_{f}\;{\overset {\textstyle }{ \underset {\textstil }{-\!\!\!-\!\!\!\!-\!\!\!\rightharpoonup \!\!\!}}}\;\ J$$

där J indikerar en korsning.

Sänkor är element som representerar utgången för ett system. De representeras på samma sätt som källor, men har pilen som pekar in i elementet istället för bort från det.

$$J\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\! -\!\!\!\rightharpoonup \!\!\!}}}\;\ S_{e}\qquad {\text{and}}\qquad J\;{\overset {\textstyle }{\underset { \textstil }{-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\!}}}\;\ S_{f}$$

Tröghet

Tröghetselement betecknas med ett stort "I", och har alltid kraft som flyter in i dem. Tröghetselement är element som lagrar energi. Vanligast är dessa en massa för mekaniska system och induktorer för elektriska system.

$$J\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!\!\!\!\!\rightharpoonup \!\!\!}}}\;\ I$$

Motstånd

Motståndselement betecknas med ett stort "R", och har alltid kraft som flyter in i dem. Motståndselement är element som avleder energi. Vanligast är dessa spjäll för mekaniska system och motstånd för elektriska system.

$$J\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!\!\!\!\!\rightharpoonup \!\!\!}}}\;\ R$$

Efterlevnad

Överensstämmelseelement betecknas med stort "C" och har alltid kraft som flyter in i dem. Överensstämmelseelement är element som lagrar potentiell energi. Vanligast är dessa fjädrar för mekaniska system och kondensatorer för elektriska system.

$$J\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!\!\!\!\!\rightharpoonup \!\!\!}}}\;\ C$$

Tvåportselement

Dessa element har två portar. De används för att ändra kraften mellan eller inom ett system. Vid konvertering från det ena till det andra förloras ingen ström under överföringen. Elementen har en konstant som kommer att ges med sig. Konstanten kallas transformatorkonstant eller gyratorkonstant beroende på vilket element som används. Dessa konstanter kommer vanligtvis att visas som ett förhållande under elementet.

Transformator

En transformator tillämpar ett förhållande mellan flöde i flöde ut, och ansträngning i ansträngning ut. Exempel inkluderar en idealisk elektrisk transformator eller en spak .

Betecknas

$${\begin{matrix}{\overset {\textstyle _{1}}{\underset {\textstyle }{\!\!\!- \!\!\!-\!\!\!\!-\!\!\!\rightharpoonup }}}\ \ \ TR\ \ {\overset {\textstyle _{2}}{\underset {\textstyle }{ \!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}\ \\^{r:1}\end{matris}}$$

där r betecknar transformatorns modul. Detta betyder

$$f_{1}r=f_{2}$$

och

$$e_{2}r=e_{1}$$

Gyrator

En gyrator tillämpar ett förhållande mellan flöde i ansträngning ut och ansträngning i flöde ut. Ett exempel på en gyrator är en likströmsmotor, som omvandlar spänning (elektrisk kraft) till vinkelhastighet (mekaniskt vinkelflöde).

$${\begin{matrix}{\overset {\textstyle _{1}}{\underset {\textstyle }{\!\!\!- \!\!\!-\!\!\!\!-\!\!\!\rightharpoonup }}}\ \ \ GY\ \ {\overset {\textstyle _{2}}{\underset {\textstyle }{ \!\!\!-\!\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}\ \\^{g:1}\end{matris}}$$

betyder att

$$e_{2}=gf_{1}$$

och

$$e_{1}=gf_{2}.$$

Flerportselement

Junctions, till skillnad från de andra elementen, kan ha valfritt antal portar antingen in eller ut. Junctions delar upp kraften över sina hamnar. Det finns två distinkta korsningar, 0-korsningen och 1-korsningen som endast skiljer sig åt i hur ansträngning och flöde förs över. Samma korsning i serie kan kombineras, men olika korsningar i serie kan inte.

0-korsningar

0-korsningar beter sig så att alla ansträngningsvärden (och dess tidsintegral/derivata) är lika över bindningarna, men summan av flödesvärdena in är lika med summan av flödesvärdena ut, eller motsvarande, alla flöden summerar till noll. I en elektrisk krets är 0-övergången en nod och representerar en spänning som delas av alla komponenter i den noden. I en mekanisk krets är 0-övergången en koppling mellan komponenter och representerar en kraft som delas av alla komponenter som är anslutna till den.

$${\text{alla }}e{\text{s är lika}}$$

$$\summa f_{\text{in}}=\summa f_{\text{out}}$$

Ett exempel visas nedan.

$${\overset {\textstyle _{1}}{\underset {\textstyle }{-\!\!\!-\!\!\!\!-\ !\!\!\rightharpoondown }}}{\stackrel {\textstyle {\stackrel {\textstyle _{2}}{\upharpoonright }}}{0}}{\overset {\textstyle _{3}}{\ underset {\textstil }{-\!\!\!-\!\!\!\!-\!\!\!\rightharpoondown }}}$$

Resulterande ekvationer:

$$e_{1}=e_{2}=e_{3}$$

$$f_{1}=f_{2}+f_{3}$$

1-korsningar

1-korsningar beter sig motsatta 0-korsningar. 1-korsningar beter sig så att alla flödesvärden (och dess tidsintegral/derivata) är lika över bindningarna, men summan av ansträngningsvärdena i är lika med summan ansträngningsvärdena ut, eller motsvarande, alla ansträngningar summerar till noll. I en elektrisk krets representerar 1-övergången en seriekoppling mellan komponenter. I en mekanisk krets representerar 1-korsningen en hastighet som delas av alla komponenter som är anslutna till den.

$${\text{alla }}f{\text{ är lika}}$$

$$\sum e_{\text{in}}=\summa e_{\text{out}}$$

Ett exempel visas nedan.

$${\overset {\textstyle _{1}}{\underset {\textstyle }{-\!\!\!-\!\!\!- \!\!\!\rightharpoondown }}}{\stackrel {\textstyle {\stackrel {\textstyle _{2}}{\upharpoonright }}}{1}}{\overset {\textstyle _{3}}{ \underset {\textstil }{-\!\!\!-\!\!\!\!-\!\!\!\rightharpoondown }}}$$

Resulterande ekvationer:

$$f_{1}=f_{2}=f_{3}$$

$$e_{1}=e_{2}+e_{3}$$

Kausalitet

Bond-grafer har en uppfattning om kausalitet, som indikerar vilken sida av en bindning som bestämmer den momentana ansträngningen och vilken som bestämmer det momentana flödet. När man formulerar de dynamiska ekvationerna som beskriver systemet, definierar kausaliteten, för varje modelleringselement, vilken variabel som är beroende och vilken som är oberoende. Genom att sprida orsakssambandet grafiskt från ett modelleringselement till det andra blir analys av storskaliga modeller lättare. Att slutföra kausal tilldelning i en bond-grafmodell kommer att tillåta detektering av modelleringssituationer där en algebraisk loop existerar; det är situationen när en variabel definieras rekursivt som en funktion av sig själv.

Som ett exempel på kausalitet, betrakta en kondensator i serie med ett batteri. Det är inte fysiskt möjligt att ladda en kondensator direkt, så allt som är parallellkopplat med en kondensator kommer nödvändigtvis att ha samma spänning (ansträngningsvariabel) som över kondensatorn. På liknande sätt kan en induktor inte ändra flödet omedelbart och därför kommer varje komponent i serie med en induktor nödvändigtvis att ha samma flöde som induktorn. Eftersom kondensatorer och induktorer är passiva enheter kan de inte bibehålla sin respektive spänning och flöde på obestämd tid – komponenterna som de är anslutna till kommer att påverka deras respektive spänning och flöde, men endast indirekt genom att påverka deras ström respektive spänning.

Obs: Kausalitet är ett symmetriskt samband. När den ena sidan "orsakar" ansträngning, "orsakar" den andra sidan flyt.

I bondningsgrafnotation kan ett kausalt slag läggas till i ena änden av kraftbindningen för att indikera att denna sida definierar flödet . Följaktligen styr den sida som är motsatt från det tillfälliga slaget ansträngningen .

Flödeskällor ( ${\displaystyle S_{f}} ) definierar flöde, så de$ värd för orsaksslaget:

$$S_{f}\;|\!\!\!-\!\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\!$$

Ansträngningskällor ( $S_{e}$ ) definierar ansträngning, så den andra änden är värd för orsaksslaget:

$$S_{e}\;-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\!|$$

Betrakta en motor med konstant vridmoment som driver ett hjul, dvs en källa till ansträngning ( ${\displaystyle S_{e}})$ . Det skulle ritas enligt följande:

$${\begin{array}{r}{\text{motor}}\\S_{e}\end{array}}\;{\overset {\textstyle \tau }{\underset {\ textstil \omega }{-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\!|}}}\;{\text{hjul}}$$

Symmetriskt definierar sidan med kausalslaget (i detta fall hjulet) flödet för bindningen.

Kausalitet resulterar i kompatibilitetsbegränsningar. Uppenbarligen kan bara ena änden av en kraftbindning definiera ansträngningen och därför kan endast ena änden av en bindning (den andra änden) ha ett kausalt slag. Dessutom kan de två passiva komponenterna med tidsberoende beteende, $I$ och $C$ , bara ha en sorts orsak: en $I$ -komponent bestämmer flödet; en $C$ -komponent definierar ansträngning. Så från en korsning, $J$ , är den föredragna kausala orienteringen som följer:

$$J\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!\!\!\!\!\rightharpoonup \ !\!\!|}}}\;I\qquad {\text{and}}\qquad J\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\ !\!\!-\!\!\!-\!\!\!\rightharpoonup }}}\;C$$

Anledningen till att detta är den föredragna metoden för dessa element kan analyseras ytterligare om du tar hänsyn till ekvationerna de skulle ge visat av tillståndets tetraeder.

$$f(t)={\frac {1}{I}}\int e (t)\,dt\qquad {\text{och}}\qquad e(t)={\frac {1}{C}}\int f(t)\,dt$$

De resulterande ekvationerna involverar integralen av den oberoende effektvariabeln. Detta är att föredra framför resultatet av att ha kausaliteten åt andra hållet, vilket resulterar i derivat. Ekvationerna kan ses nedan.

$$e(t)=I{\dot {f}}(t)\qquad {\text{and} }\qquad f(t)=C{\dot {e}}(t)$$

Det är möjligt för en bindningsgraf att ha en kausal stapel på ett av dessa element på det icke-föredragna sättet. I ett sådant fall sägs en "orsakskonflikt" ha inträffat vid det bandet. Resultaten av en orsakskonflikt ses endast när man skriver tillstånd-rymd- ekvationerna för grafen. Det förklaras mer detaljerat i det avsnittet.

Ett motstånd har inget tidsberoende beteende: applicera en spänning och få ett flöde omedelbart, eller applicera ett flöde och få en spänning omedelbart, sålunda kan ett motstånd befinna sig i vardera änden av en orsaksbindning:

$$J\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!\!-\!\!\!\rightharpoonup \ !\!\!|}}}\;R\qquad {\text{and}}\qquad J\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!\!-\ !\!\!-\!\!\!-\!\!\!\rightharpoonup }}}\;R$$

Transformatorer är passiva, varken försvinner eller lagrar energi, så kausalitet passerar genom dem:

$$\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!\!\!\!\!\!-\!\ !\!-\!|}}}\;TF\;{\översatt {\textstil }{\underset {\textstil }{-\!\!\!-\!\!\!\!-\!\!\ !-\!\!\!-\!|}}}\;\qquad {\text{eller}}\qquad \;{\overset {\textstyle }{\underset {\textstyle }{|\!\! \!-\!\!\!-\!\!\!-\!\!\!-\!\!\!-}}}\;TF\;{\overset {\textstyle }{\underset { \textstil }{|\!\!\!-\!\!\!-\!\!\!\!-\!\!\!-\!\!\!-}}}\;$$

En gyrator förvandlar flöde till ansträngning och ansträngning till flöde, så om flöde orsakas på ena sidan, orsakas ansträngning på den andra sidan och vice versa:

$$\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\!\!\!-\!\!\!\!-\!\ !\!-\!\!\!-}}}\;GY\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\ !\!\!-\!\!\!-\!|}}}\;\qquad {\text{eller}}\qquad \;{\overset {\textstyle }{\underset {\textstyle }{- \!\!\!-\!\!\!\!-\!\!\!-\!\!\!-\!|}}}\;GY\;{\overset {\textstyle }{\underset { \textstil }{|\!\!\!-\!\!\!-\!\!\!\!-\!\!\!-\!\!\!-}}}\;$$

Korsningar

I en 0-korsning är ansträngningarna lika; i en 1-korsning är flödena lika. Med kausala bindningar kan alltså endast en bindning orsaka ansträngningen i en 0-korsning och endast en kan orsaka flödet i en 1-korsning. Således, om kausaliteten för en bindning av en korsning är känd, är kausaliteten för de andra också känd. Det ena bandet kallas det "starka bandet"

$${\text{strong bond}}\rightarrow \;\dashv \!{\overset {\textstyle \top }{\underset {\textstyle \bot }{0}}}\!\dashv \qquad {\text{and}}\qquad {\text{strong bond}}\rightarrow \;\vdash \!{\overset {\textstyle \bot }{\ underset {\textstyle \top }{1}}}\!\vdash$$

I ett nötskal måste 0-korsningar ha en enda kausalstapel, 1-korsningar måste ha alla utom en kausalstapel.

Att fastställa kausalitet

För att fastställa kausaliteten för en obligationsgraf måste vissa steg följas. Dessa steg är:

1. Rita Källa Orsaksstaplar
2. Draw Föredragen kausalitet för C- och I-bindningar
3. Rita kausala staplar för 0- och 1-övergångar, transformatorer och gyratorer
4. Rita R-bindning kausala staplar
5. Om en orsakskonflikt uppstår, ändra C eller I bindning till differentiering

En genomgång av stegen visas nedan.

$$displaystyle {\begin{matrix}S_{f}&{\overset {\ textstil }{\underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle } {\underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&TR&{\overset {\textstyle }{\ underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset { \textstyle }{\!\!\!-\!\!\!-\!\!\!\!-\!\!\!\rightharpoonup }}}&C_{5}\\&&\downharpoonleft &&^{r: 1}&&\downharpoonleft &&\\&&C_{2}&&&&R_{6}&&\end{matrix}}}$$

Det första steget är att dra kausalitet för källorna, över vilka det bara finns en. Detta resulterar i grafen nedan.

$${\begin{matrix}S_{f}&{\overset {\textstyle } {\underset {\textstyle }{|\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{ \underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&TR&{\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\ textstil }{\!\!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&C_{5}\\&&\downharpoonleft &&^{r:1 }&&\downharpoonleft &&\\&&C_{2}&&&&R_{6}&&\end{matrix}}$$

Nästa steg är att dra den föredragna kausaliteten för C-bindningarna.

$${\begin{matrix}S_{f}&{\overset {\textstyle }{\underset {\textstyle }{|\!\! \!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\textstyle }{\!\!\! -\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&TR&{\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\ !\!\!-\!\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\! \!\!-\!\!\!-\!\!\!\rightharpoonup }}}&C_{5}\\&&{\bar {\downharpoonleft }}&&^{r:1}&&\downharpoonleft &&\ \&&C_{2}&&&&R_{6}&&\end{matris}}$$

Tillämpa sedan kausaliteten för 0- och 1-övergångarna, transformatorerna och gyratorerna.

$${\begin{matrix}S_{f}&{\overset {\textstyle }{\underset {\textstyle }{|\!\ !\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\textstyle }{|\!\! \!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&TR&{\overset {\textstyle }{\underset {\textstyle }{|\!\!\ !-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\textstyle }{|\!\!\! -\!\!\!-\!\!\!\!\!\!\!\rightharpoonup }}}&C_{5}\\&&{\bar {\downharpoonleft }}&&^{r:1}&&{ \underline {\downharpoonleft }}&&\\&&C_{2}&&&&R_{6}&&\end{matris}}$$

Det finns dock ett problem med 0-korsningen till vänster. 0-korsningen har två kausalstaplar vid korsningen, men 0-korsningen vill ha en och bara en vid korsningen. Detta orsakades av att ${\textstyle C_{2}}$ var i den föredragna kausaliteten. Det enda sättet att fixa detta är att vända den kausala stapeln. Detta resulterar i en orsakskonflikt, den korrigerade versionen av grafen är nedan, med ⋆ { $textstyle \star }$ som representerar orsakskonflikten.

$${\begin{matrix}S_{f}&{\overset {\textstyle }{\underset {\textstyle }{|\! \!\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\textstyle }{|\!\ !\!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&TR&{\overset {\textstyle }{\underset {\textstyle }{|\!\! \!-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&0&{\overset {\textstyle }{\underset {\textstyle }{|\!\!\ !-\!\!\!-\!\!\!-\!\!\!\rightharpoonup }}}&C_{5}\\&&{\underline {\downharpoonleft }}\star &&^{r:1 }&&{\underline {\downharpoonleft }}&&\\&&C_{2}&&&&R_{6}&&\end{matrix}}$$

Konvertering från andra system

En av de största fördelarna med att använda bindningsgrafer är att när du väl har en bindningsgraf spelar det ingen roll den ursprungliga energidomänen. Nedan är några av stegen att tillämpa när du konverterar från energidomänen till en obligationsgraf.

Elektromagnetisk

Stegen för att lösa ett elektromagnetiskt problem som en bindningsgraf är följande:

1. Placera en 0-korsning vid varje nod
2. Infoga källor, R-, I-, C-, TR- och GY-bindningar med 1-korsningar
3. Jord (båda sidor om en transformator eller gyrator finns)
4. Tilldela kraftflödesriktning
5. Förenkla

Dessa steg visas tydligare i exemplen nedan.

Linjär mekanisk

Stegen för att lösa ett linjärmekaniskt problem som en bindningsgraf är följande:

1. Placera 1-korsningar för varje distinkt hastighet (vanligtvis vid en massa)
2. Infoga R- och C-bindningar vid sina egna 0-korsningar mellan 1-övergångarna där de verkar
3. Infoga Källor och I-bindningar på 1-korsningarna där de verkar
4. Tilldela kraftflödesriktning
5. Förenkla

Dessa steg visas tydligare i exemplen nedan.

Förenkla

Förenklingssteget är detsamma oavsett om systemet var elektromagnetiskt eller linjärt mekaniskt. Stegen är:

1. Ta bort Bond med noll effekt (på grund av jord eller noll hastighet)
2. Ta bort 0- och 1-övergångar med mindre än tre bindningar
3. Förenkla parallell kraft
4. Kombinera 0 korsningar i serie
5. Kombinera 1 korsningar i serie

Dessa steg visas tydligare i exemplen nedan.

Parallell kraft

Parallell effekt är när kraften går parallellt i en bindningsgraf. Ett exempel på parallell effekt visas nedan.

Parallell effekt kan förenklas genom att återkalla förhållandet mellan ansträngning och flöde för 0- och 1-korsningar. För att lösa parallell potens kommer du först att vilja skriva ner alla ekvationer för korsningarna. För exemplet som tillhandahålls kan ekvationerna ses nedan. (Notera sifferbindningen som variabeln ansträngning/flöde representerar).

$${\begin{matrix}f_{1}=f_{2}=f_{3}&&e_{2}=e_{4}=e_{7 }\\e_{1}=e_{2}+e_{3}&&f_{2}=f_{4}+f_{7}\\&&\\e_{3}=e_{5}=e_{6} &&f_{7}=f_{6}=f_{8}\\f_{3}=f_{5}+f_{6}&&e_{7}+e_{6}=e_{8}\end{matrix}}$$

Genom att manipulera dessa ekvationer kan du ordna dem så att du kan hitta en ekvivalent uppsättning av 0- och 1-korsningar för att beskriva den parallella potensen.

Till exempel, eftersom ${\textstyle e_{3}=e_{6}}$ och ${\textstyle e_{2}=e_{7}}$ kan du ersätta variablerna i ekvationen ${\textstyle e_{1}=e_{2}+e_{3}}$ vilket resulterar i ${\textstyle e_{1}=e_{6}+e_{ 7}}$ och eftersom ${\textstyle e_{6}+e_{7}=e_{8}}$ vet vi nu att $e_{1}=e_ {8}$ . Detta samband mellan två ansträngningsvariabler som är lika kan förklaras av en 0-korsning. Genom att manipulera andra ekvationer kan du finna att $f_{4}=f_{5}$ som beskriver förhållandet mellan en 1-korsning. När du har bestämt vilka relationer du behöver kan du rita om den parallella kraftsektionen med de nya korsningarna. Resultatet för exemplet visas nedan.

Exempel

Enkelt elsystem

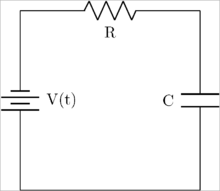
En enkel elektrisk krets som består av en spänningskälla, motstånd och kondensator i serie.

Det första steget är att rita 0-korsningar vid alla noder:

$${\begin{matrix}&0&&0&\\&&&&\\&&&&\\&0&&0&\end{matrix}}$$

Nästa steg är att lägga till alla element som verkar i sin egen 1-korsning:

$${\begin{matrix}&&&&R&&&\\&&&&|&&&&\\&&0&-&1&-&0&&\\\&&|&&&&|&&\\S_{e}&-&1&&&&1&-&C\\&&|&&&&| &&\\&&{\underline {0}}&-&-&-&0&&\end{matris}}$$

Nästa steg är att välja en mark. Jorden är helt enkelt en 0-korsning som kommer att antas sakna spänning. I detta fall kommer marken att väljas till den nedre vänstra 0-korsningen, som är understruken ovan. Nästa steg är att rita alla pilar för bindningsgrafen. Pilarna på korsningar ska peka mot marken (följer en liknande väg som ström). För motstånds-, tröghets- och följsamhetselement pekar pilarna alltid mot elementen. Resultatet av att rita pilarna kan ses nedan, med 0-korsningen markerad med en stjärna som marken.

Nu när vi har Bond-grafen kan vi börja processen med att förenkla den. Det första steget är att ta bort alla marknoder. Båda de nedre 0-korsningarna kan tas bort, eftersom de båda är jordade. Resultatet visas nedan.

Därefter kan korsningarna med mindre än tre bindningar tas bort. Detta beror på att flöde och ansträngning passerar genom dessa korsningar utan att modifieras, så de kan tas bort så att vi kan dra mindre. Resultatet kan ses nedan.

Det sista steget är att tillämpa kausalitet på obligationsgrafen. Att tillämpa kausalitet förklarades ovan. Den slutliga obligationsgrafen visas nedan.

Avancerat elsystem

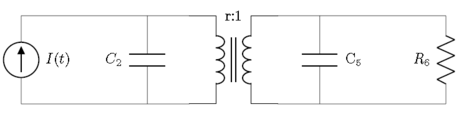
Ett mer avancerat elektriskt system med en strömkälla, motstånd, kondensatorer och en transformator

Att följa stegen med denna krets kommer att resultera i bindningsdiagrammet nedan, innan det förenklas. Noderna markerade med stjärnan anger marken.

Att förenkla bindningsdiagrammet kommer att resultera i bilden nedan.

Slutligen kommer användning av kausalitet att resultera i obligationsdiagrammet nedan. Bandet med stjärnan betecknar en orsakskonflikt.

Enkel linjär mekanisk

Ett enkelt linjärt mekaniskt system, bestående av en massa på en fjäder som är fäst på en vägg. Massan har en viss kraft som appliceras på den. En bild på systemet visas nedan.

För ett mekaniskt system är det första steget att placera en 1-korsning vid varje distinkt hastighet, i detta fall finns det två distinkta hastigheter, massan och väggen. Det är vanligtvis bra att märka 1-korsningarna som referens. Resultatet är nedan.

$${\begin{matrix}&&\\&&\\1_{\text{mass}}&&\\&&\\&&\\&&\\1_{\text{wall}}&&\end {matris}}$$

Nästa steg är att rita R- och C-bindningarna vid sina egna 0-korsningar mellan 1-korsningarna där de verkar. För detta exempel finns det bara en av dessa bindningar, C-bindningen för våren. Den verkar mellan 1-korsningen som representerar massan och 1-korsningen som representerar väggen. Resultatet är nedan.

$${\begin{matrix}&&\\&&\\1_{\text{mass}}&&\\|&&\\0&-&C:{\frac {1}{k}}\\|&& \\1_{\text{vägg}}&&\end{matris}}$$

Därefter vill du lägga till källorna och I-bindningarna på 1-korsningen där de verkar. Det finns en källa, källan till ansträngning (kraft) och en I-bindning, massans massa som båda verkar på massans 1-korsning. Resultatet visas nedan.

$${\begin{matrix}S_{e}:F(t)&&\\|&&\\1_{\text{mass}}&-&I:m\\|&&\\\0&-&C: {\frac {1}{k}}\\|&&\\1_{\text{vägg}}&&\end{matris}}$$

Nästa effektflöde ska tilldelas. Liksom de elektriska exemplen ska ström flyta mot marken, i detta fall väggens 1-korsning. Undantag från detta är R,C eller I-bindning, som alltid pekar mot elementet. Den resulterande obligationsgrafen är nedan.

Nu när obligationsgrafen har genererats kan den förenklas. Eftersom väggen är jordad (har noll hastighet) kan du ta bort den korsningen. Som sådan kan 0-korsningen C-bindningen är på, också tas bort eftersom den då kommer att ha mindre än tre bindningar. Den förenklade obligationsgrafen kan ses nedan.

Det sista steget är att tillämpa kausalitet, den slutliga bindningsgrafen kan ses nedan.

Avancerad linjär mekanisk

Ett mer avancerat linjärt mekaniskt system kan ses nedan.

Precis som exemplet ovan är det första steget att göra 1-korsningar vid var och en av de avlägsna hastigheterna. I det här exemplet finns det tre avlägsna hastigheter, Mass 1, Mass 2 och väggen. Sedan ansluter du alla bindningar och tilldelar kraftflöde. Obligationen kan ses nedan.

Därefter börjar du processen med att förenkla bindningsgrafen genom att ta bort 1-korsningen av väggen och ta bort korsningar med mindre än tre bindningar. Obligationsgrafen kan ses nedan.

Det finns parallell effekt i bindningsgrafen. Att lösa parallell effekt förklarades ovan. Resultatet av att lösa det kan ses nedan.

Till sist, tillämpa kausalitet, den slutliga bindningsgrafen kan ses nedan.

Tillståndsekvationer

När väl en bindningsgraf är klar kan den användas för att generera systemets ekvationer för representation av tillstånd och rymd . State-space representation är särskilt kraftfull eftersom den tillåter komplexa multi-orders differentialsystem att lösas som ett system av första ordningens ekvationer istället. Den allmänna formen av tillståndsekvationen är

$${\dot {\mathbf {x} }}(t)=\mathbf {A} \mathbf {x} (t)+\ mathbf {B} \mathbf {u} (t)$$

där ${\textstyle \mathbf {x} (t)}$ är en kolumnmatris av tillståndsvariablerna eller systemets okända. ${\textstyle {\dot {\mathbf {x} }}(t)}$ är tidsderivatan av tillståndsvariablerna. ${\textstyle \mathbf {u} (t)}$ är en kolumnmatris av systemets ingångar. Och ${\textstyle \mathbf {A} }$ och ${\textstyle \mathbf {B} }$ är matriser av konstanter baserade på systemet. Tillståndsvariablerna för ett system är ${\textstyle q(t)}$ och ${\textstyle p(t)}$ värden för varje C- och I-bindning utan en kausal konflikt. Varje I-bindning får en ${\textstyle p(t)}$ medan varje C-bindning får en ${\textstyle q(t)}$ .

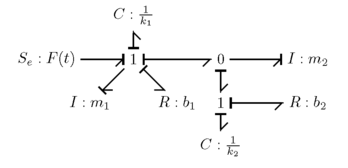
Till exempel, om du har följande obligationsdiagram

du skulle ha följande ${\textstyle {\dot {\mathbf {x} }}(t)}$ , ${\textstyle \mathbf {x} (t)}$ och ${\textstyle \mathbf {u} (t)}$ matriser:

$${\dot {\mathbf {x} }}(t)={\begin{bmatrix}{\dot {p}}_{3}(t)\\{\dot {q}}_{ 6}(t)\end{bmatrix}}\qquad {\text{and}}\qquad \mathbf {x} (t)={\begin{bmatrix}p_{3}(t)\\q_{6} (t)\end{bmatrix}}\qquad {\text{and}}\qquad \mathbf {u} (t)={\begin{bmatrix}e_{1}(t)\end{bmatrix}}$$

Matriserna för ${\textstyle \mathbf {A} }$ och ${\textstyle \mathbf {B} }$ löses genom att bestämma förhållandet mellan tillståndsvariablerna och deras respektive element, som beskrevs i tillståndets tetraeder. Det första steget för att lösa tillståndsekvationerna är att lista alla de styrande ekvationerna för obligationsgrafen. Tabellen nedan visar sambandet mellan obligationer och deras styrande ekvationer.

Elementtyp	Bond namn	Bind med kausalitet	Styrande ekvationer)
Enkelportselement	Källa/Sink, S	$S_{e}\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\ !\!|}}}\;$	${\text{input}}=e(t)$
		$S_{f}\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\!\!\!-\!\!\!- \!\!\!\rightharpoonup }}}\;$	${\text{input}}=f(t)$
	Motstånd, R: Försvunnen energi	$\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\! |}}}\ R$	$f(t)={\frac {1}{R}}e(t)$
		$\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\!\!\!-\!\!\!-\!\ !\!\rightharpoonup }}}\ R$	$e(t)=Rf(t)$
	Tröghet, jag: Rörelseenergi	♦ $\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\! |}}}\ I$	$f(t)={\frac {1}{I}}\int e(t)\,dt$
		$\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\!\!\!-\!\!\!-\!\ !\!\rightharpoonup }}}\ I$	$e(t)=I{\dot {f}}(t)$
	Efterlevnad, C: Potentiell energi	$\;{\overset {\textstyle }{\underset {\textstyle }{-\!\!\!-\!\!\!-\!\!\!\rightharpoonup \!\!\! |}}}\ C$	$f(t)=C{\dot {e}}(t)$
		♦ $\;{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\!\!\!-\!\!\!-\!\ !\!\rightharpoonup }}}\ C$	$e(t)={\frac {1}{C}}\int f(t)\,dt$
Dubbelportselement	Transformator, TR	${\begin{matrix}{\overset {\textstyle }{{\underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\ !\!\!\rightharpoonup }}|}}\ TR\ \ {\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!\!-\!\!\ !-\!\!\!\rightharpoonup }}}|\ \\^{r:1}\end{matris}}$	$f_{1}r=f_{2}$ $e_{2}r=e_{1}$
		${\begin{matrix}|\ {\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!-\!\ !\!-\!\!\!\rightharpoonup }}}\ TR\ \ |\ {\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!- \!\!\!-\!\!\!\rightharpoonup }}}\ \\^{r:1}\end{matris}}$
	Gyrator, GY	${\begin{matrix}|\ {\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!- \!\!\!\rightharpoonup }}}\ GY{\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!-\!\!\!-\ !\!\!\rightharpoonup }}}|\ \\^{g:1}\end{matris}}$	$f_{1}g=e_{2}$ $f_{2}g=e_{1}$
		${\begin{matrix}\ {\overset {\textstyle }{\underset {\textstyle }{\!\!\!-\!\!\!-\!\! \!-\!\!\!\rightharpoonup }}}|\ GY{\overset {\textstyle }{\underset {\textstyle }{|\!\!\!-\!\!\!\!-\!\ !\!-\!\!\!\rightharpoonup }}}\ \\^{g:1}\end{matris}}$
Flerportselement	0 korsning	En och bara en kausal bar vid korsningen	${\text{all }}e(t)=$
			$\summa f(t)_{\text{in}}=\summa f(t)_{\text{out}}$
	1 korsning	en och bara en orsak bar bort från korsningen	$\sum e(t)_{\text{in}}=\summa e(t)_{\text{out}}$
			${\text{all }}f(t)=$

"♦" betecknar föredragen kausalitet.

För det angivna exemplet,

de styrande ekvationerna är följande.

1. ${\textstyle {\text{input}}=e_{1}}$
2. ${\textstyle e_{1}=e_{2}+e_{3}+e_{4}}$
3. ${\textstil f_{1}=f_{2}=f_{3}=f_{4}}$
4. ${\textstyle e_{2}=R_{2}f_{2}}$
5. ${\textstyle f_{3}={\frac {1}{I_{3}}}\int e_{3}\,dt={\ frac {1}{I_{3}}}p_{3}}$
6. ${\textstil f_{4}\cdot r=f_{5}}$
7. ${\textstyle e_{5}\cdot r=e_{4}}$
8. ${\textstyle e_{5}=e_{6}=e_{7}}$
9. ${\textstil f_{5}=f_{6}+f_{7}}$
10. ${\textstyle e_{6}={\frac {1}{C_{6}}}\int f_{6}\,dt={\ frac {1}{C_{6}}}q_{6}}$
11. ${\textstyle f_{7}={\frac {1}{R_{7}}}e_{7}}$

Dessa ekvationer kan manipuleras för att ge tillståndsekvationerna. För det här exemplet försöker du hitta ekvationer som relaterar ${\textstyle {\dot {p}}_{3}(t)}$ och ${\textstyle {\dot { q}}_{6}(t)}$ i termer av ${\textstyle p_{3}(t)}$ , ${\textstyle q_{6}(t)}$ , och ${\textstyle e_{1}(t)}$ .

För att börja bör du komma ihåg från tillståndets tetraeder att ${\textstyle {\dot {p}}_{3}(t)=e_{3}(t)}$ börjar med ekvation 2 kan du ordna om den så att $e_{3}=e_{1}-e_{2}-e_{4}$ . $e_{2}$ kan ersätta ekvation 4, medan i ekvation 4 kan $f_{2}$ ersättas med $f_{3}$ på grund av ekvation 3 , som sedan kan ersättas av ekvation 5. $e_{4}$ kan likaså ersättas med ekvation 7, där $e_{5}$ kan ersättas med $e_ {6}$ som sedan kan ersättas med ekvation 10. Efter dessa substituerade ger den första tillståndsekvationen som visas nedan.

$${\dot {p}}_{3 }(t)=e_{3}(t)=e_{1}(t)-{\frac {R_{2}}{I_{3}}}p_{3}(t)-{\frac {r }{C_{6}}}q_{6}(t)$$

Den andra tillståndsekvationen kan likaså lösas genom att komma ihåg att ${\textstyle {\dot {q}}_{6}(t)=f_{6}(t)}$ . Den andra tillståndsekvationen visas nedan.

$${\dot {q}}_{6}(t) =f_{6}(t)={\frac {r}{I_{3}}}p_{3}(t)-{\frac {1}{R_{7}\cdot C_{6}}}q_ {6}(t)$$

Båda ekvationerna kan vidare omarrangeras till matrisform. Resultatet är nedan.

$${\begin{bmatrix}{\dot {p}}_{3}(t)\\{\dot {q}}_{6}(t)\end {bmatrix}}={\begin{bmatrix}-{\frac {R_{2}}{I_{3}}}&-{\frac {r}{C_{6}}}\\{\frac {r }{I_{3}}}&-{\frac {1}{R_{7}\cdot C_{6}}}\end{bmatrix}}{\begin{bmatrix}p_{3}(t)\\ q_{6}(t)\end{bmatrix}}+{\begin{bmatrix}1\\0\end{bmatrix}}{\begin{bmatrix}e_{1}(t)\end{bmatrix}}$$

Vid denna punkt kan ekvationerna behandlas som vilket annat problem som helst med representation av tillstånd och rymd .

Internationella konferenser om modellering av obligationsdiagram (ECMS och ICBGM)

En bibliografi om modellering av obligationsdiagram kan extraheras från följande konferenser:

• ECMS-2013 27:e Europeiska konferensen om modellering och simulering, 27–30 maj 2013, Ålesund, Norge
• ECMS-2008 22:a Europeiska konferensen om modellering och simulering, 3–6 juni 2008 Nicosia, Cypern
• ICBGM-2007: 8th International Conference on Bond Graph Modeling And Simulation, 15–17 januari 2007, San Diego, Kalifornien, USA
• ECMS-2006 20th European Conference on Modeling and Simulation, 28–31 maj 2006, Bonn, Tyskland
• IMAACA-2005 International Mediterranean Modeling Multiconference
• ICBGM-2005 International Conference on Bond Graph Modeling and Simulation, 23–27 januari 2005, New Orleans, Louisiana, USA – Papers
• ICBGM-2003 International Conference on Bond Graph Modeling and Simulation (ICBGM'2003) 19–23 januari 2003, Orlando, Florida, USA – Papers
• 14:E Europeiska simuleringssymposium 23–26 oktober 2002 Dresden, Tyskland
• ESS'2001 13th European Simulation symposium, Marseille, Frankrike 18–20 oktober 2001
• ICBGM-2001 International Conference on Bond Graph Modeling and Simulation (ICBGM 2001), Phoenix, Arizona, USA
• European Simulation Multi-konferens 23-26 maj 2000, Gent, Belgien
• 11:e europeiska simuleringssymposium, 26–28 oktober, 1999 Castle, Friedrich-Alexander University, Erlangen-Nürnberg, Tyskland
• ICBGM-1999 International Conference on Bond Graph Modeling and Simulation 17–20 januari 1999 San Francisco, Kalifornien
• ESS-97 9TH European Simulation Symposium and Exhibition Simulation in Industry, Passau, Tyskland, 19–22 oktober 1997
• ICBGM-1997 3rd International Conference on Bond Graph Modeling And Simulation, 12–15 januari 1997, Sheraton-Crescent Hotel, Phoenix, Arizona
• 11:e European Simulation Multiconference Istanbul, Turkiet, 1–4 juni 1997
• ESM-1996 10:e årliga European Simulation Multiconference Budapest, Ungern, 2–6 juni 1996
• ICBGM-1995 Int. Konf. om Bond Graph Modeling and Simulation (ICBGM'95), 15–18 januari 1995, Las Vegas, Nevada.

Se även

• 20-sim simuleringsprogram baserad på obligationsgrafteorin
• AMESim- simuleringsmjukvara baserad på teorin om obligationsgraf
• Hybridbindningsdiagram
• Samenergi

Vidare läsning

•   Kypuros, Javier (2013). Systemdynamik och styrning med obligationsgrafmodellering . Boca Raton: Taylor&Francis. doi : 10.1201/b14676 . ISBN 978-1-4665-6075-8 .
•   Paynter, Henry M. (1960). Analys och design av tekniska system . MIT Press. ISBN 0-262-16004-8 .
•   Karnopp, Dean C.; Margolis, Donald L.; Rosenberg, Ronald C. (1990). Systemdynamik: ett enhetligt tillvägagångssätt . New York: John Wiley & Sons. ISBN 0-471-62171-4 .
•   Thoma, Jean Ulrich (1975). Bondgrafer: introduktion och tillämpningar . Oxford: Pergamon Press. ISBN 0-08-018882-6 .
•   Gawthrop, Peter J.; Smith, Lorcan PS (1996). Metamodellering: bindningsgrafer och dynamiska system . London: Prentice Hall. ISBN 0-13-489824-9 .
•   Brown, Forbes T. (2007). Teknisk systemdynamik – ett enhetligt grafcentrerat tillvägagångssätt . Boca Raton: Taylor & Francis. ISBN 0-8493-9648-4 .
•   Mukherjee, Amalendu; Karmakar, Ranjit (2000). Modellering och simulering av tekniska system genom bondgraphs . Boca Raton: CRC Press. ISBN 978-0-8493-0982-3 .
•   Gawthrop, PJ; Ballance, DJ (1999). "Kapitel 2: Symbolisk beräkning för manipulering av hierarkiska bindningsdiagram". I Munro, N. (red.). Symboliska metoder i styrsystemanalys och design . London: Institution of Electrical Engineers. s. 23-52 . ISBN 0-85296-943-0 .
•   Borutzky, Wolfgang (2010). Bond Graph Methodology . London: Springer. doi : 10.1007/978-1-84882-882-7 . ISBN 978-1-84882-881-0 .
• http://www.site.uottawa.ca/~rhabash/ESSModelFluid.pdf Förklarar modellering av bindningsgrafen i fluiddomänen
• http://www.dartmouth.edu/~sullivan/22files/Fluid_sys_anal_w_chart.pdf Förklarar modellering av bindningsgrafen i fluiddomänen

externa länkar

• Simscapes officiella MATLAB/Simulink-tilläggsbibliotek för grafisk programmering av bindningsdiagram
• BG V.2.1 Freeware MATLAB/Simulink tilläggsbibliotek för grafisk obligationsgrafprogrammering