Samenergi

Grafisk definition av samenergi

Inom fysik och teknik är samenergi (eller samenergi ) en icke-fysisk storhet, mätt i energienheter, som används i teoretisk analys av energi i fysiska system.

Begreppet samenergi kan appliceras på många konservativa system (tröghetsmekaniska, elektromagnetiska, etc.), som kan beskrivas genom ett linjärt förhållande mellan inmatad och lagrad energi.

Samenergianalysteknikerna kan inte tillämpas på icke-linjära system. Små olinjäriteter försummas dock ofta genom linearisering av problemen.

Exempel - magnetisk samenergi

Tänk på ett system med en enkel spole och en orörlig armatur (IE inget mekaniskt arbete utförs). Följaktligen lagras all elektrisk energi som tillförs enheten i magnetfältet.

$$dW_{\text{input}}=dW_{\text{lagrad}}\qquad (dW_{\text{mekanisk}}=0)$$

där ( e är spänningen , i är strömmen och $\lambda$ är flödeskopplingen ):

$$dW_{\text{input}}=ei\,dt$$

$$dW_{\text{lagrad}}=i\,d\lambda$$

därför

$$dW_{\text{lagrad}}=ei\,dt=i\,d\lambda$$

För ett allmänt problem är förhållandet $i-\lambda$ icke-linjärt (se även magnetisk hysteres ) .

Om det finns en ändlig förändring i flödeskopplingen från ett värde till ett annat (t.ex. från $\lambda _{1}$ till $\lambda _{2}$ ) kan beräknas som:

$$\Delta W_{\text{stored}}=\int _{\lambda _{1}}^{\lambda _{2}}i (\lambda )\,d\lambda$$

(Om förändringarna är cykliska kommer det att uppstå förluster för hysteres och virvelströmmar. Den extra energin för detta skulle tas från ingångsenergin, så att flödeskopplingen till spolen inte påverkas av förlusterna och spolen kan behandlas som en idealisk förlustfri spole. Ett sådant system är därför konservativt.)

För beräkningar kan antingen flödeskopplingen $\lambda$ eller strömmen i användas som oberoende variabel.

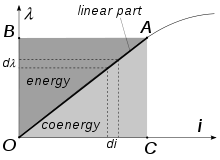
Den totala energin som lagras i systemet är lika med arean OABO, som i sin tur är lika med OACO, därför:

$$\mathrm {Energy} =\operatörsnamn {Area} (OABO)=W_{\text{ lagrad}}=\int _{0}^{\lambda }i(\lambda )\,d\lambda$$

$$\mathrm {Coenergy} =\operatörsnamn {Area} (OACO)=W' _{\text{lagrad}}=\int _{0}^{i}\lambda (i)\,di$$

För linjära förlustfria system är samenergin lika i värde som den lagrade energin. samenergin har ingen egentlig fysisk betydelse, men den är användbar för att beräkna mekaniska krafter i elektromagnetiska system. För att skilja den från den "riktiga" energin i beräkningar markeras den vanligtvis med en apostrof.

Den totala arean av rektangeln OCABO är lika med summan av de två trianglarna (energi + samenergi), så:

$$\operatörsnamn {Area} (OCABO)=\operatörsnamn {Area} (OABO)+\operatörsnamn {Area} (OACO)$$

Därför för vid en given arbetspunkt med ström i och flödeskoppling $\lambda$ :

$$\mathrm {Energy} (W)+\mathrm {Coenergy} (W')=i\lambda$$

Självinduktansen definieras som flödeslänkning över ström :

$$L={\frac {\lambda }{i}}$$

och energin som lagras i en spole är:

$$W_{\text{energi}}={\frac {1}{2}}{\frac {\lambda ^{2}}{L} }={\frac {1}{2}}Li^{2}$$

I en magnetisk krets med en rörlig armatur kommer induktansen L ( x ) att vara en funktion av position x .

Man kan därför skriva att fältenergin är en funktion av två matematiskt oberoende variabler $\lambda$ och x :

$$W(\lambda ,x)_{\text{energy}}={\frac {1}{2}}\,{\frac {\lambda ^{2}}{L(x)}}$$

Och samenergi är en funktion av två oberoende variabler i och x :

$$W'(i,x)_{\text{samenergi}}={\frac {1}{2}}L(x) i^{2}$$

De två sista uttrycken är allmänna ekvationer för energi och samenergi i magnetostatiska system.

Tillämpningar av samenergiteori

Begreppet samenergi används praktiskt till exempel i finita elementanalys för beräkningar av mekaniska krafter mellan magnetiserade delar.